Dynamic Response and Oscillating Behaviour of Fractionally Damped Beam

Dynamic Response and Oscillating Behaviour of Fractionally Damped Beam

Diptiranjan Behera1and S.Chakraverty2

This paper presents the numerical solution of a viscoelastic continuous beam whose damping behaviours are defined in term of fractional derivatives of arbitrary order.Homotopy Perturbation Method(HPM)is used to obtain the dynamic response with respect to unit impulse load.Obtained results are depicted in term of plots.Comparisons are made with the analytic solutions obtained by Zu-feng and Xiao-yan(2007)to show the effectiveness and validation of the present method.

Viscoelastic beam,Fractional derivative,Impulse response function,Homotopy Perturbation Method(HPM).

1 Introduction

In recent years,fractional calculus has been used to model physical and engineering problems such as in solid mechanics, fluid mechanics,biology,physics,and other areas of engineering and science.Since,it is too difficult to obtain the exact solution of fractional differential equation so,one may need a reliable and efficient numerical technique for the solution of fractional differential equations.Many important works have been reported regarding fractional calculus in the last few decades.Relating to this field several excellent books have also been written by different authors representing the scope and various aspects of fractional calculus such as[Oldham and Spanier(1974);Kiryakov(1993);Miller and Ross(1993);Samko et al.(1993);Podlubny(1999)].These books also give an extensive review on fractional derivative and fractional differential equations which may help the reader for understating the basic concepts of fractional calculus.As regards,many authors[Shukla et al.(2014);Wang et al.(2011,2014);Ye and Ding(2009)]have developed various methods to solve fractional ordinary and partial differential equations and integral equations of physical systems.Most commonly used methods are Adomian Decomposition Method(ADM),Variational Iteration Method(VIM),Differential Transform Method(DTM),etc.which are described in[Momani(2005a,2005b,2007,2008);Arikoglu and Ozkol(2007);Das(2008);Gejji and Jafari(2009)]and the references mentioned therein.Chen et al.(2014a,2014b)used Haar wavelet method for the numerical solution of fractional order differential equations.

Some other related works are reviewed and cited here as follows for a better understanding of the present investigation.Half-order fractional derivative models of viscoelastically damped structures has been studied by Bagley and Torvik(1983a,1983b)in an excellent way.Laplace transform is considered in Bagley and Torvik(1983b)to find the response characteristics.Also,Koeller(1984)has taken a fractional model to describe creep and relaxation functions for viscoelastic materials.In Gaul et al.(1989,1991)Fourier transformation is used to analyse the damping description of impulse response function of oscillators with fractional derivative.Time domain finite element analysis of viscoelastic structures with fractional derivative is clearly explained in Enelund and Josefson(1997).Eigenvector expansion method is successfully implemented in Suarez and Shokooh(1997)to find the solution of a dynamic systems containing fractional derivative.Various numerical methods are applied in[Enelund and Josefson(1997);Goren flo(1997);Enelund and Olsson(1999);Shokooh and Suarez(1999);Yuan and Agrawal(2002)]to find the responses of fractionally damped system.

Recently,homotopy perturbation method is found to be a powerful tool for analysing this type of system involving fractional derivatives.The Homotopy Perturbation Method(HPM)was first developed by He(1999,2000,2003,2005,2006)and many authors applied this method to solve various linear and non-linear functional equations of scientific and engineering problems.The solution is considered as the sum of in finite series,which converges rapidly to accurate solutions.In the homotopy technique(in topology),a homotopy is constructed with an embedding parameter which is considered as a"small parameter".Very recently homotopy perturbation method has been applied to a wide class of physical problems[Wang(2007,2008);Yildirim(2009);Biazara and Eslamib(2011);Behera and Chakravety(2013);Chakraverty and Behera(2013)].Also very recently Chakraverty and Tapaswini(2014)have used HPM for the uncertainty analysis of fuzzy fractional Fornberg-Whitham equation.

In the present analysis,the homotopy perturbation method is used to handle the dynamic analysis of a fractionally damped viscoelastic continuous beam.Same problem is studied by Zu-feng and Xiao-yan(2007)by adomain decomposition method.Damping factor is defined with fractional derivative of an arbitrary or-der.In the following sections preliminaries are first given.Then implementation of HPM for fractionally damped viscoelastic beam is discussed.Next response analysis for unit impulse load is presented.Lastly numerical examples and conclusions are given.

2 Preliminaries

In this section,we present some notations,definitions and preliminary facts which are used further in this paper[Oldham and Spanier(1974);Samko et al.(1993);Kiryakov(1993);Miller and Ross(1993);Podlubny(1999);Behera and Chakravety(2013);Chakraverty and Behera(2013)].

Definition 1 Riemann-Liouville fractional integral:

There are several definitions of fractional integral.The most commonly used definition is of Riemann-Liouville and Caputo[Podlubny(1999)].The Riemann-Liouville integral operator Jαof order α ≥ 0,is defined by

Definition 2 Caputo derivative:

The fractional derivative of f(t)in the Caputo sense is defined as

where,the parameter α is the order of the derivative and it is allowed to be real or even complex.In this paper,only real and positive α will be considered.For the Caputo’s derivative we have

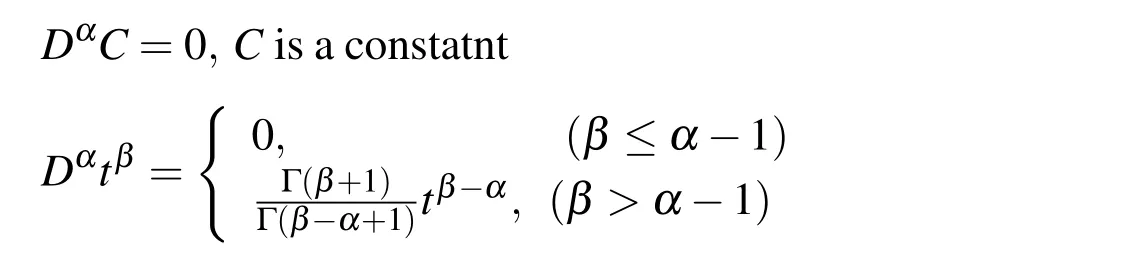
Similar to integer-order differentiation,Caputo’s fractional differentiation is linear operation:

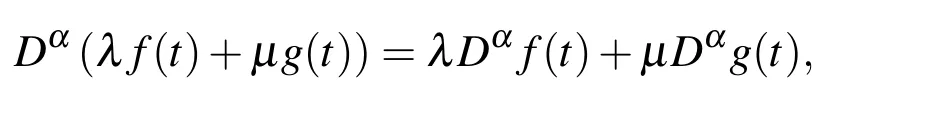
where λ ,µ are constants and satisfies so called Leibnitz rule:

if f(τ)is continuous in[0,t]and g(τ)has n+1 continuous derivative in[0,t].

Definition 3 Mittage-Leffer function:

A two-parameter function of the Mittage-Leffer type is defined by the series expansion[Podlubny(1999)]as

3 Application of HPM[He(1999,2000)]to fractionally damped viscoelastic beam

To develop numerical schemes for a fractionally damped viscoelastic beam[Zufeng and Xiao-yan(2007)]let us consider a linear differential equation which describes the dynamics of the system with the damping as arbitrary fractional derivative of order α

where ρ,A,c,E and I represents the mass density,cross sectional area,damping coefficients per unit length,Young’s modulus of elasticity and moment of inertia of the beam.F(x,t)is the externally applied force and v(x,t)is the transverse displacement.is the fractional derivative of order α ∈ (0,1)of the displacement function v(x,t).Initial conditions are considered asandHomogeneous initial conditions are taken here to compare the solution obtained by the present HPM with the solution of[Zu-feng and Xiao-yan(2007)].

Eq.(1)can be written as

According to HPM,we may construct a simple homotopy for an embedding parameter p∈[0,1]as follows

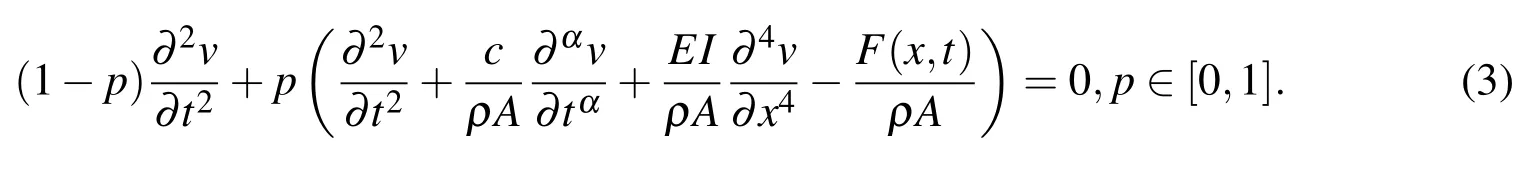
or

Here,p is considered as a small homotopy parameter 0≤p≤1.For p=0,Eqs.(3)and(4)become a linear equation i.e.which is easy to solve.For p=1,Eqs.(3)and(4)turns out to be same as the original Eq.(1)or(2).This is called deformation in topologyandare called homotopic.

Next,we can assume the solution of Eq.(3)or(4)as a power series expansion in p as

where vi(x,t)for i=0,1,2,...are functions yet to be determined.Substituting Eq.(5)into Eq.(3)or(4),and equating the terms with the identical power of p we can obtain a series of equations of the form

and so on.

Choosing initial approximation v0(x,0)=0 and applying the operator(which is the inverse of the operatoron both sides of Eqs.(6)to(10)one may obtain the following equations

and so on.

Now substituting these terms in Eq.(5)with p→1 one may get the approximate solution of Eq.(1)as follows.

The solution series converge very rapidly.The rapid convergence means that only few terms are required to get the approximate solutions.

4 Response analysis

Similar to[Zu-feng and Xiao-yan(2007)]the external applied force is considered as

where,F(x,t)is a specified space dependent deterministic function and g(t)is time dependent process.In this section we consider response subject to a unit impulsive load g(t)= δ(t),where δ(t)is the unit impulse function.By using HPM we have

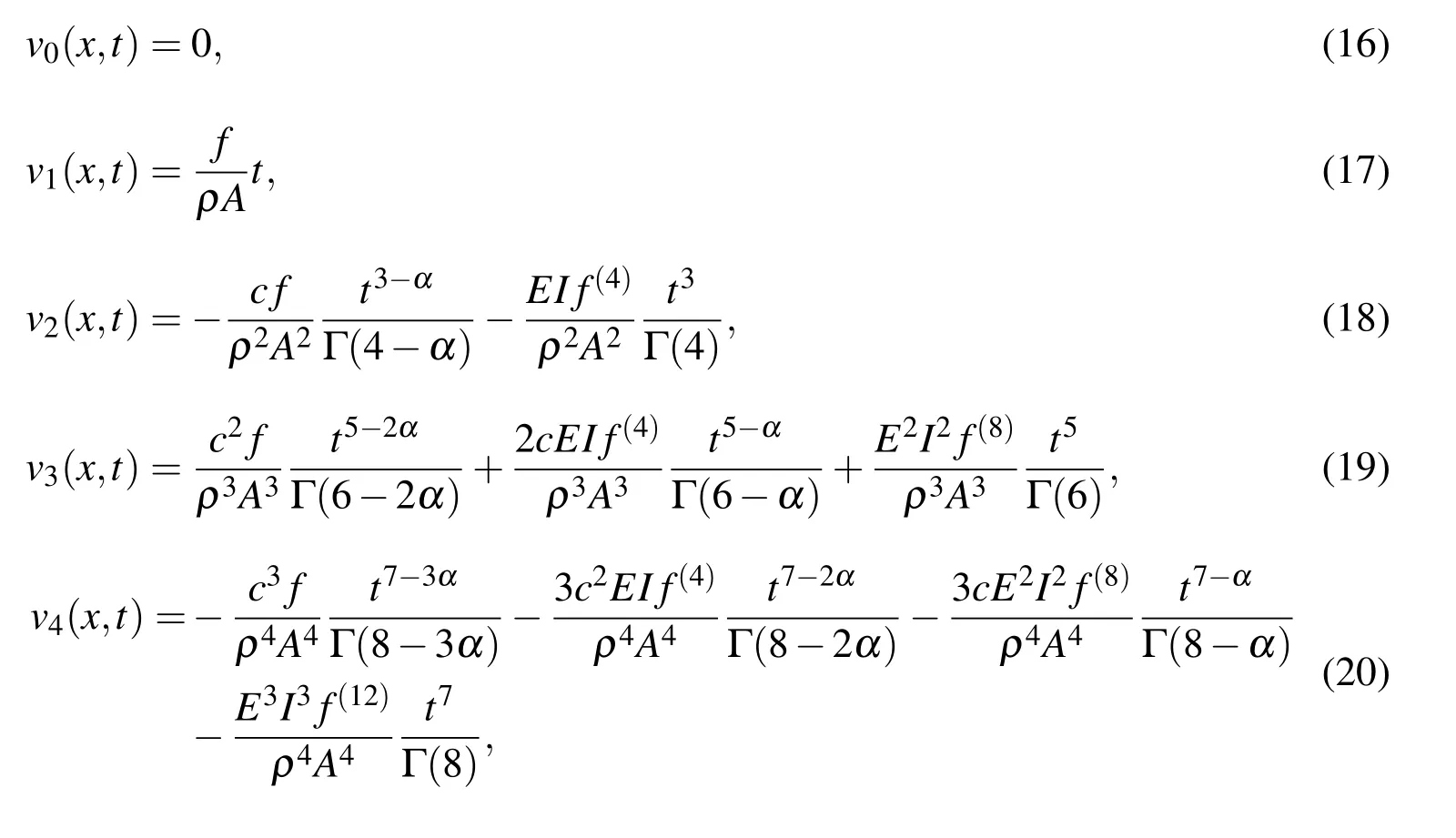
In the similar manner the rest of the components can be obtained.Therefore,the solution can be written in the general form as

Eq.(21)can be rewritten as follows

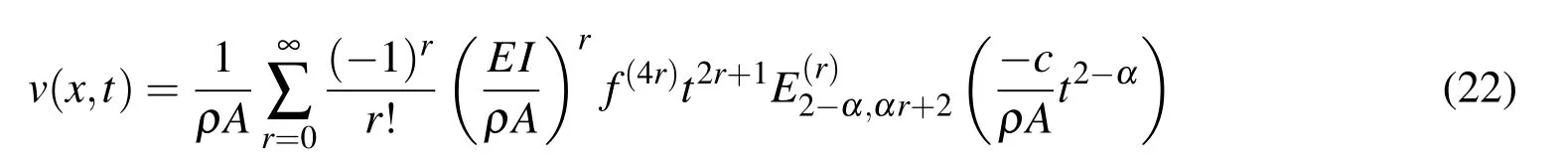
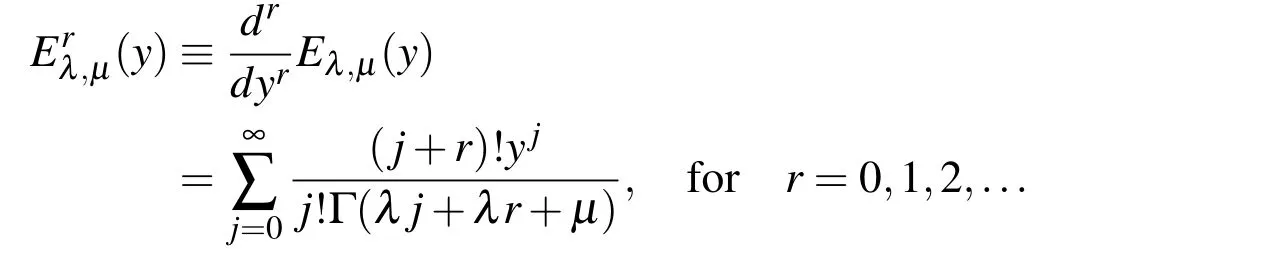
For impulse response λ=2−α and µ=αr+2.

5 Results and Discussions

As discussed above,here unit impulse function response have been considered for the present analysis.Computed results are depicted in term of plots.

Eq.(21)or(22)provides the desired expressions for the considered loading condition.The results obtained by HPM are similar to the analytical solution presented in Zu-feng and Xiao-yan(2007).In order to show the responses in a precise way,some numerical results are presented in this section.As we have considered a simply supported beam,hence one may have the expression for the force distribution for single degree freedom idealization as

Here the numerical computation has been done by truncating the in finite series(21)or(22)to a finite number of terms.For numerical simulations,let us denote c/m and EI/ρA as 2ηω3/2and ω2respectively where,ω is the natural frequency and η is the damping ratio.The values of the parameters are taken as ρA=1,L= π and m=1.

Figure 1:Impulse responses along x=1/2 with natural frequency(a)ω=5rad/s,(b)ω =10rad/s and damping ratio η =0.5.

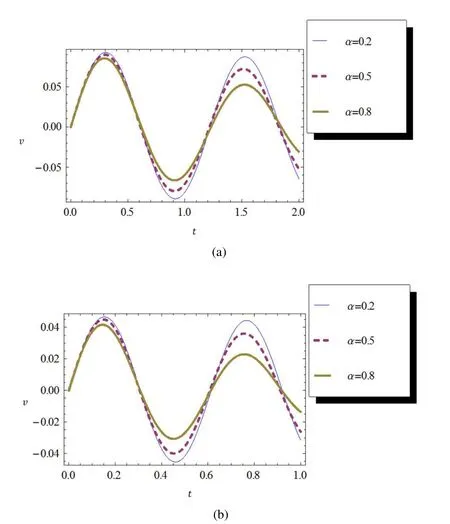
Figure 2:Impulse responses along x=1/2 with natural frequency(a)ω=5rad/s,(b)ω =10rad/s and damping ratio η =0.05.

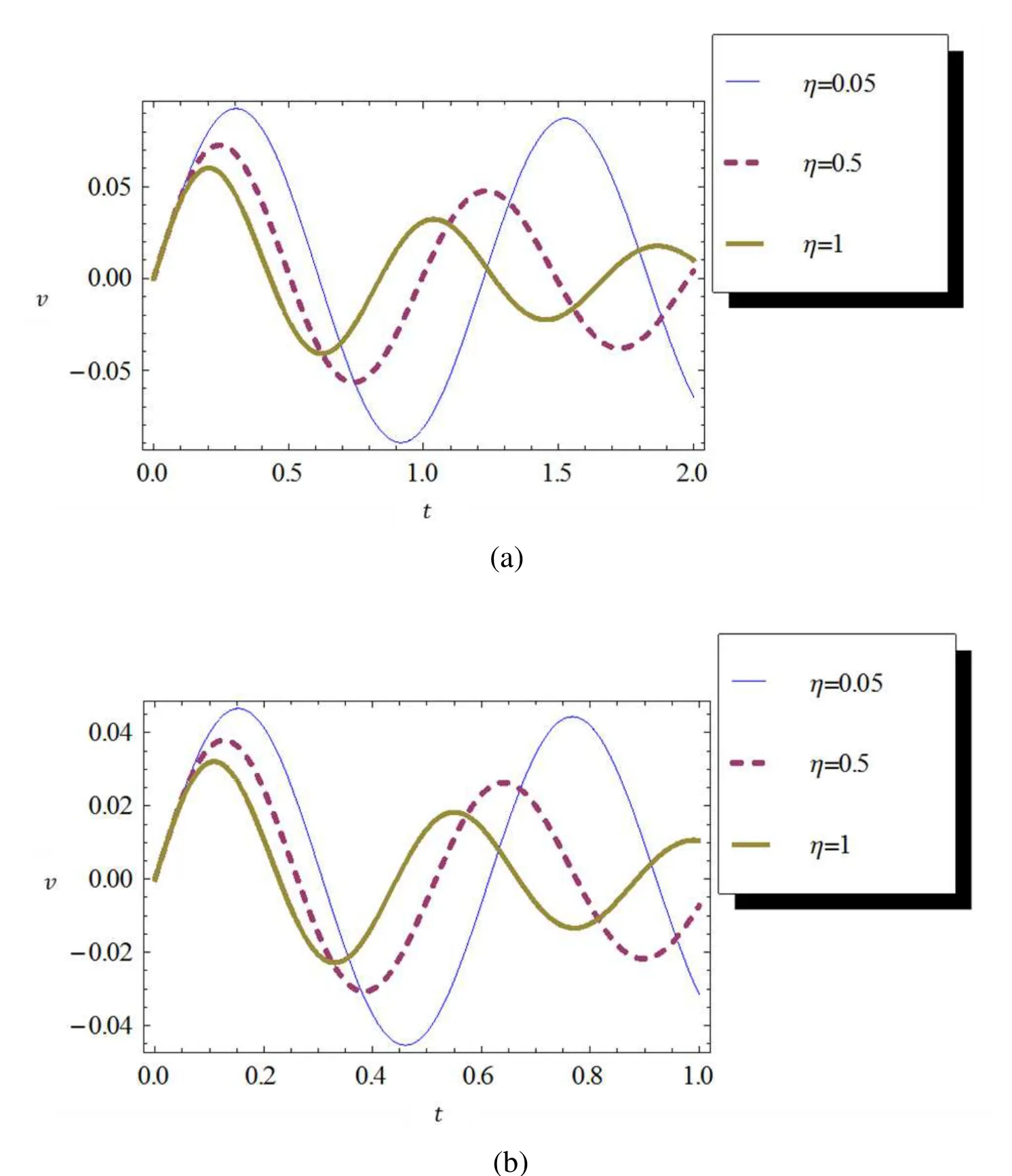
Figure 3:Impulse responses along x=1/2 with natural frequency(a)ω=5rad/s,(b)ω =10rad/s and α =0.2.

Figure 4:Impulse responses along x=1/2 with natural frequency(a)ω=5rad/s,(b)ω =10rad/s and α =0.5.

Fig.(1)gives effect of displacement on time for various values of α(=0.2,0.5,0.8).In this computation x and η are taken as 1/2.Figs.1(a)and 1(b)present the plot for ω =5rad/s and ω =10rad/s respectively.Similar simulation has been done for damping ratio η=0.05 and obtained results are depicted in Fig.2.Next for different values of η(=0.05,0.5,1)dynamic responses versus time are given in Fig.3.In this computation α=0.2 and x=1/2 are considered.Again Figs.3(a)and 3(b)depict the plot for ω=5rad/s and 10rad/s respectively.Finally Fig.4 cites the results as above with α=0.5.

It is interesting to note from Figs.(1)and(2)that if we increase the order of the fractional derivative α.This means that the beam suffers more oscillations for smaller value of α.Similar observations may be made by keeping the order of the fractional derivative constant and varying the damping ratios as shown in Figs.(3)and(4).It may clearly be seen that increase of the value of the damping ratios decrease the oscillations.

6 Conclusions

Homotopy perturbation method has successfully been applied to the solution of a fractionally damped viscoelastic beam,where the fraction derivative is considered as of arbitrary order.The impulse response functions with homogeneous initial conditions are chosen to illustrate the proposed method.The performance of this method is shown and its result are compared with analytical solution obtained by Zu-feng and Xiao-yan(2007).From the present results it is interesting to note that by increasing the order of the fractional derivative the beam suffers less oscillation.Similar observations have also been made by keeping the order of the fractional derivative constant and varying the damping ratios.Though the solution by HPM is of the form of an in finite series,it can be written in a closed form in some cases.The main advantage of HPM is the capability to achieve exact solution and rapid convergences with few terms.It is interesting to note that the results obtained by present method exactly matches with the analytical solution of Zu-feng and Xiaoyan(2007).One may also considered uncertainty in the initial condition or in system parameters in term of fuzzy to have the bounds of variations in responses.

Acknowledgement:The authors would like to thank the editor and anonymous reviewers for valuable comments and suggestions that have led to an improvement in both the quality and clarity of the paper.

Arikoglu,A.;Ozkol,I.(2007):Solution of fractional differential equations by using differential transform method.Chaos Solitons Fract.,vol.34,pp.1473-1481.

Bagley,R.L.;Torvik,P.J.(1983a):A theoretical basis for the application of fractional calculus to viscoelasticity.J.Rheol.,vol.27,pp.201-210.

Bagley,R.L.;Torvik,P.J.(1983b):Fractional calculus-a different approach to the analysis of viscoelastically damped structures.AIAA J.,vol.21,pp.741-748.

Behera,D.;Chakraverty,S.(2013):Numerical solution of fractionally damped beam by homotopy perturbation method.Cent.Eur.J.Phys.,vol.11,pp.792-798.

Biazara,J.;Eslamib,M.(2011):A new homotopy perturbation method for solving systems of partial differential equations.Comp.Math.Appl.,vol.62,pp.225-234.

Chakraverty,S.;Behera,D.(2013):Dynamic responses of fractionally damped mechanical system using homotopy perturbation method.Alexandria Eng.J.,vol.52,pp.557-562.

Chakraverty,S.;Tapaswini,S.(2014):Non probabilistic solution of fuzzy fractional Fornberg-Whitham equation.Comp.Mod.Eng.Sci.,vol.103,pp.71-90.

Chen,Y.;Han,X.;Liu,L.(2014a):Numerical solution for a class of linear system of fractional differential equations by the Haar wavelet method and the convergence analysis.Comp.Mod.Eng.Sci.,vol.97,pp.391-405.

Chen,Y.;Liu,L.;Li,X.;Sun,Y.(2014b):Numerical solution for the variable order time fractional diffusion equation with Bernstein polynomials.Comp.Mod.Eng.Sci.,vol.97,pp.81-100.

Das,S.(2008):Solution of fractional vibration equation by the variational iteration method and modified decomposition method.Int.J.Nonlin.Sci.Numer.Simul.,vol.10,pp.361-365.

Enelund,M.;Josefson,B.L.(1997):Time domain finite element analysis of viscoelastic structures with fractional derivative constitutive relations.AIAA J.,vol.35,pp.1630-1637.

Enelund,M.;Olsson,P.(1999):Time domain modeling of damping using anelastic displacement fields and fractional calculus.Int.J.Solids Struct.,vol.36,pp.939-970.

Gaul,L.;Klein,P.;Kemple,S.(1991):Damping Description Involving Fractional Operators.Mech.Syst.Signal Process.,vol.5,pp.8-88.

Gaul,L.;Klein,P.;Kemple,S.(1989):Impulse response function of an oscillator with fractional derivative in damping description.Mech.Res.Commun.,vol.16,pp.4447-4472.

Gejji,V.D.;Jafari,H.(2007):Solving a multi-order fractional differential equation using Adomian decomposition.Appl.Math.Comp.,vol.189,pp.541-548.

Goren flo,R.(1997):Fractional Calculus:Some Numerical Methods,Fractals and Fractional Calculus in Continuum Mechanics.Springer Verlag,New York.

He,J.H.(2000):A coupling method of a homotopy technique and a perturbation technique for non-linear problems.Int.J.Nonlin.Mech.,vol.35,pp.37-43.

He,J.H.(2003):Homotopy perturbation method:a new nonlinear analytical technique.Appl.Math.Comput.,vol.135,pp.73-79.

He,J.H.(1999):Homotopy perturbation technique.Comput.Meth.Appl.Mech.Eng.,vol.178,pp.257-262.

He,J.H.(2005):Homotopy perturbation method for bifurcation of nonlinear problems.Int.J.Nonlin.Sci.Numer.Simul.,vol.6,pp.207-208.

He,J.H.(2006):Homotopy perturbation method for solving boundary value problems.Phys.Lett.A,vol.350,pp.87-88.

Kenneth,S.;Ross,B.(1993):An Introduction to the Fractional Calculus and Fractional Differential Equations.John Wiley and Sons,New York.

Kiryakova,V.S.(1993):Generalized Fractional Calculus and Applications.Longman Scientific and Technical,England.

Koeller,R.C.(1984):Application of fractional calculus to the theory of viscoelasticity.ASME J.Appl.Mech.Vol.51,pp.299-307.

Li,B.(2014):Numerical solution of fractional Fredholm-Volterra integro-differential equations by means of generalized hat functions method.Comp.Mod.Eng.Sci.,vol.99,pp.105-122.

Momani,S.(2005a):Analytic and approximate solutions of the space-and timefractional telegraph equations.Appl.Math.Comput.,vol.170,pp.1126-1134.

Momani,S.(2005b):An explicit and numerical solutions of the fractional kdv equation.Math.Comput.Simul.vol.70,pp.110-118.

Momani,S.;Ibrahim,R.(2007):Analytical solutions of a fractional oscillator by the decomposition method.Int.J.Pure Appl.Math.,vol.37,pp.119-132.

Momani,S.;Odibat,Z.;Alawneh,A.(2008):Variational iteration method for solving the space-and time-fractional kdv equation.Numer.Meth.Part.Differ.Equat.,vol.24,pp.262-271.

Oldham,K.B.;Spanier,J.(1974):The Fractional Calculus.Academic Press,NewYork.

Podlubny,I.(1999):Fractional Differential Equations.Academic Press,NewYork.

Samko,S.G.;Kilbas,A.A.;Marichev,O.I.(1993):Fractional Integrals and Derivatives-Theory and Applications.Gordon and Breach Science Publishers,Langhorne.

Shokooh,A.;Suarez,L.E.(1999):A comparison of numerical methods applied to a fractional model of damping.J.Vib.Control,vol.5,pp.331-354.

Shukla,H.S.;Tamsir,M.;Srivastava,V.K.;Kumar,J.(2014):Approximate analytical solution of time-fractional order Cauchy reaction diffusion equation.Comp.Mod.Eng.Sci.,vol.103,pp.1-17.

Suarez,L.E.;Shokooh,A.(1997):An eigenvector expansion method for the solution of motion containing fractional derivatives.ASME J.Appl.Mech.,vol.64,pp.629-635.

Wang,L.;Han,X.;Xie,Y.(2011):A new homotopy perturbation method for solving an ill-posed problem of multi-source dynamic loads reconstruction.Comp.Mod.Eng.Sci.,vol.82,pp.179-194.

Wang,L.;Ma,Y.;Yang,Y.(2014):Legendre polynomials method for solving a class of variable order fractional differential equation.Comp.Mod.Eng.Sci.,vol.101,pp.97-111.

Wang,Q.(2008):Homotopy perturbation method for fractional kdv-burgers equation.Chaos Solitons Fract.,vol.35,pp.843-850.

Wang,Q.(2007):Homotopy perturbation method for fractional kdv equation.Appl.Math.Comput.,vol.190,pp.1795-1802.

Ye,H.;Ding,Y.(2009):Dynamical analysis of a fractional-order HIV model.Comp.Mod.Eng.Sci.,vol.49,pp.255-268.

Yildirim,A.(2009):An algorithm for solving the fractional nonlinear schrodinger equation by means of the homotopy perturbation method.Int.J.Nonlin.Sci.Numer.Simul.,vol.10,pp.445-451.

Yuan,L.;Agrawal,O.P.(2002):A numerical scheme for dynamic systems containing fractional derivatives.J.Vib.Acoustics,vol.124,pp.321-324.

Zu-feng,L.;Xiao-yan,T.(2007):Analytical solution of fractionally damped beam by adomain decomposition Method.Appl.Math.Mech.,vol.28,pp.219-228.

1Corresponding Author.School of Mechatronics Engineering,University of Electronic Science and Technology of China,No.2006,Xiyuan Avenue,West Hi-Tech Zone,Chengdu,Sichuan 611731,P.R.China.E-mail:diptiranjanb@gmail.com

2Department of Mathematics,National Institute of Technology Rourkela,Odisha-769008,India.E-mail:sne_chak@yahoo.com