A Jacobi Spectral Collocation Scheme Based on Operational Matrix for Time-fractional Modified Korteweg-de Vries Equations

A Jacobi Spectral Collocation Scheme Based on Operational Matrix for Time-fractional Modified Korteweg-de Vries Equations

A.H.Bhrawy1,2,E.H.Doha3,S.S.Ezz-Eldien4and M.A.Abdelkawy2

In this paper,a high accurate numerical approach is investigated for solving the time-fractional linear and nonlinear Korteweg-de Vries(KdV)equations.These equations are the most appropriate and desirable definition for physical modeling.The spectral collocation method and the operational matrix of fractional derivatives are used together with the help of the Gauss-quadrature formula in order to reduce such problem into a problem consists of solving a system of algebraic equations which greatly simplifying the problem.Our approach is based on the shifted Jacobi polynomials and the fractional derivative is described in the sense of Caputo.In addition,the presented approach is applied also to solve the timefractional modified KdV equation.For testing the accuracy,validity and applicability of the developed numerical approach,we apply it to provide high accurate approximate solutions for four test problems.

KdV equation,Jacobi polynomials,Operational matrix,Gauss quadrature,Collocation spectral method,Caputo derivative

1 Introduction

In recent years,many engineering and physical scientists have interested in studying the fractional calculus(theories of derivatives and integrals with any non-integer arbitrary order)for its ability to describe many engineering,physical and mathematical phenomena,see[Alcoutlabi and Martinez-Vega(1998);Chen,Han and Liu(2014);Biswas,Bhrawy,Abdelkawy,Alshaery and Hilal(2014);Pang,Chen and Sze(2014);Kumar,Singh and Kumar(2015);Lin,Wang and Wei(2015);Garrappa(2015);Li(2014);Wang,Liu,Chen,Liu and Liu(2014);Chen,Liu,Li and Sun(2014);Sadati,Ghaderi and Ranjbar(2013);Dehghan,Abbaszadeh and Mohebbi(2015a);Kumar,Singh and Sushila(2013);Abdelkawy,Zaky,Bhrawy and Baleanu,(2015)].Furthermore,studying the properties of the fractional differential equations(differential equations with non-integer arbitrary order)and finding effective analytical and numerical solutions for them have become very important to be studied,for instance,the fractional sub-equation method[Wang and Xu(2014a)and Wang and Xu(2014b)];the kernel-based approximation technique[Dou and Hon(2014)],the predictor-corrector method[Yu,Liu,Turner and Burrage(2014)],the sumudu decomposition method[Al-Khaled(2015)];the waveform relaxation methods[Jiang and Ding(2013)],the Haar wavelet operational matrix[Ray(2012)],the fast alternating-direction finite difference method[Wang and Du(2014)],the Taylor matrix method[Gulsu,Ozturk and Anapal(2013)]and others[Wang,Du,Tan,Li and Nie(2013);Wei,Chen and Sun(2014);Shukla,Tamsir,Srivastava and Kumar(2014);Hwang and Geubelle(2000);El-Danaf and Hadhoud(2012);Wei and Zeng(2012);Valipour,Yaghoobi and Mashinchi(2014);Li,Chen and Ye(2011);Garrappa and Popolizio(2011)].Recently,the spectral methods have been used based on some orthogonal polynomials to solve highorder differential and fractional differential equations,see[Abd-Elhameed(2014);Avila,Ramos and Atluri(2009);Bhrawy and Abdelkawy(2015);Bhrawy and Zaky(2015b);Dehghan,Abbaszadeh and Mohebbi(2015b)].

The operational matrices of fractional derivatives have been derived for some types of orthogonal polynomials such as,Legendre polynomials[Saadatmandi and Dehghan(2010)],Chebyshev polynomials[Doha,Bhrawy and Ezz-Eldien(2011)]and Jacobi polynomials[Doha,Bhrawy and Ezz-Eldien(2012)]that used together with the tau-and collocation spectral methods to solve types of ordinary fractional differential equations.Also,the operational matrices of fractional integrals have been derived for some types of orthogonal polynomials such as Chebyshev polynomials[Bhrawy and Alofi(2013)],Jacobi polynomials[Doha,Bhrawy and Ezz-Eldien(2012)]and Laguerre polynomials[Bhrawy,Alghamdi and Taha(2012)]that used together with the tau-and collocation spectral methods to solve fractional differential equations.Recently,the operational matrices of fractional derivatives and those of fractional integrals have been used with the help of the tau-spectral method to solve types of partial fractional differential equations,see[Saadatmandi and Dehghan(2011);Bhrawy and Zaky(2015a);Doha,Bhrawy and Ezz-Eldien(2015)].More recently,the operational matrices have been used for obtaining the numerical solution of types of optimal control problems[Bhrawy,Doha,Baleanu,Ezz-Eldien and Abdelkawy(2015)]and the Lane-Emden type equations[Doha,Abd-Elhameed and Bassuony(2015)].

The KdV equation has been used to describe a large number of engineering and physical phenomena,see[Karpman(1998);Leblond and Sanchez(2003);Liu,Zhou,Liu and Luo(2003);Gao and Tian(2001)].The time-fractional KdV(modified KdV)equation is a generalization of the classical KdV(modified KdV)equation that obtained by replacing the first-order time derivative term by a fractional derivative one of order ν,0＜ ν ≤ 1.Wang[Wang(2007)]applied the homotopy perturbation method for an analytical solution of the fractional KdV equation,while in[El-Wakil,Abulwafa,Zahran and Mahmoud(2011)],the authors applied the He’s variational-iteration method to solve the time-fractional KdV equation.Recently,Guoatal.[Guo,Mei,Fang and Qiu(2012)]used the fractional variational iteration method based on the He’s polynomials to introduce compacton and solitary pattern solutions for the nonlinear time-fractional dispersive KdV-type equations involving Jumarie’s fractional derivative.On the other hand,Abdulaziz et al.[Abdulaziz,Hashim and Ismail(2009)]introduced the fractional modified KdV equation and applied the homotopy-perturbation method for its approximate solution,while in[Kurulay and Bayram(2010)],the authors applied the two-dimensional differential transform method for an approximate analytical solution of the fractional modified KdV equation.

The main goal of the current paper is to introduce some efficient numerical techniques to solve spectrally the time-fractional linear,nonlinear and modified KdV equations.Our numerical techniques are based on the shifted Jacobi collocation spectral method and the operational matrix of fractional derivative together with the help of the Gauss quadrature formula to reduce thus problems into a problem consists of solving a system of algebraic equations that can be solved by any iterative method.

The current paper is organized as follows.In Section 2,we introduce some definitions and notations of fractional calculus with some properties of Jacobi polynomials.In Sections 3,4 and 5,the operational matrix of fractional derivative is used together with the Jacobi tau-spectral method to solve the time-fractional linear,nonlinear and modified KdV equations,respectively.In Section 6,some numerical examples are introduced for ensuring the validity and accuracy of the presented technique.Also a conclusion is given in Section 7.

2 Preliminaries and notation

2.1 Fractional calculus definitions

Riemann-Liouville and Caputo fractional definitions are the two most used from other definitions of fractional derivatives which have been introduced recently.

Definition 1.1.The integral of order γ≥ 0(fractional)according to Riemann-

Liouville is given by

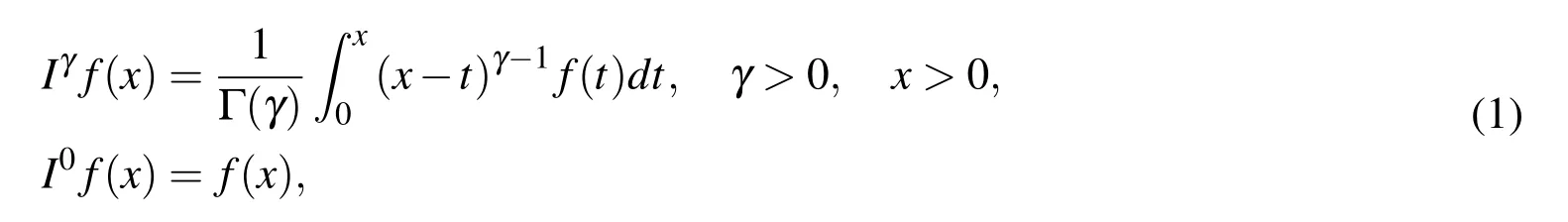
where

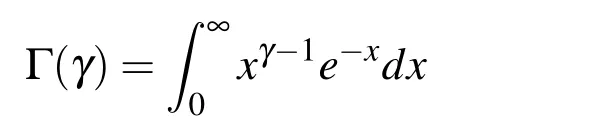
is gamma function.

The operator Iγsatis fies the following properties

Definition 1.2.The Caputo fractional derivative of order γ is defined by

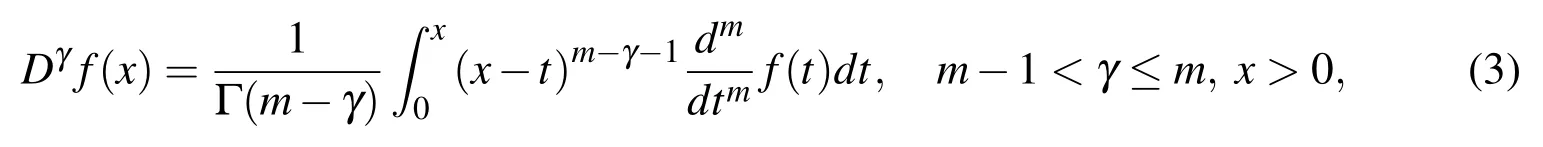
where m is the ceiling function of γ.

The operator Dγsatis fies the following properties

2.2 Shifted Jacobi polynomials

The Jacobi polynomial of degree j,denoted byand de fined on the interval[−1,1],constitute an orthogonal system with respect to the weight function ω(α,β),i.e.,

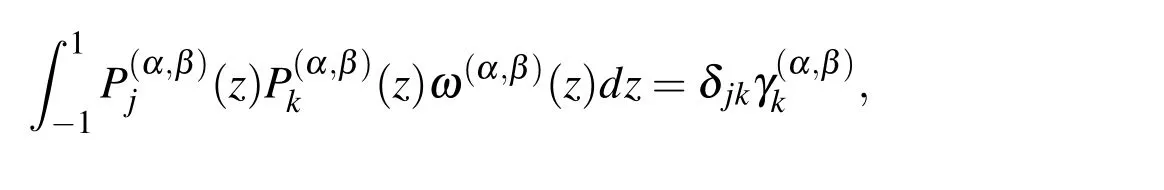
where δjkis the Kronecker function and

The shifted Jacobi polynomial of degree j,denoted byand defined on the interval[0,L],is generated by introducing the change of variableThen the shifted Jacobi polynomials are constituting an orthogonal system with respect to the weight functionwith the orthogonality property

where

The shifted Jacobi polynomials are generated from the three-term recurrence relations

with

where

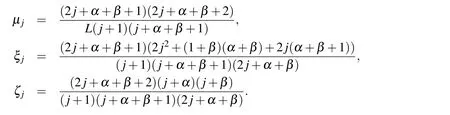
The explicit analytic form of the shifted Jacobi polynomialsof degree j is given by

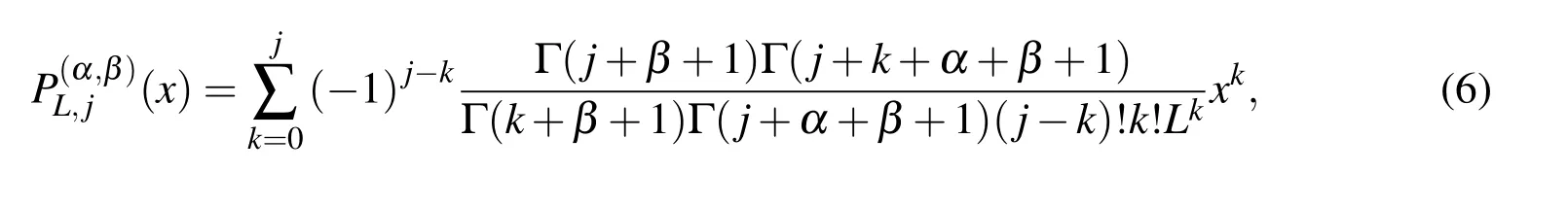
and this in turn,enables one to get

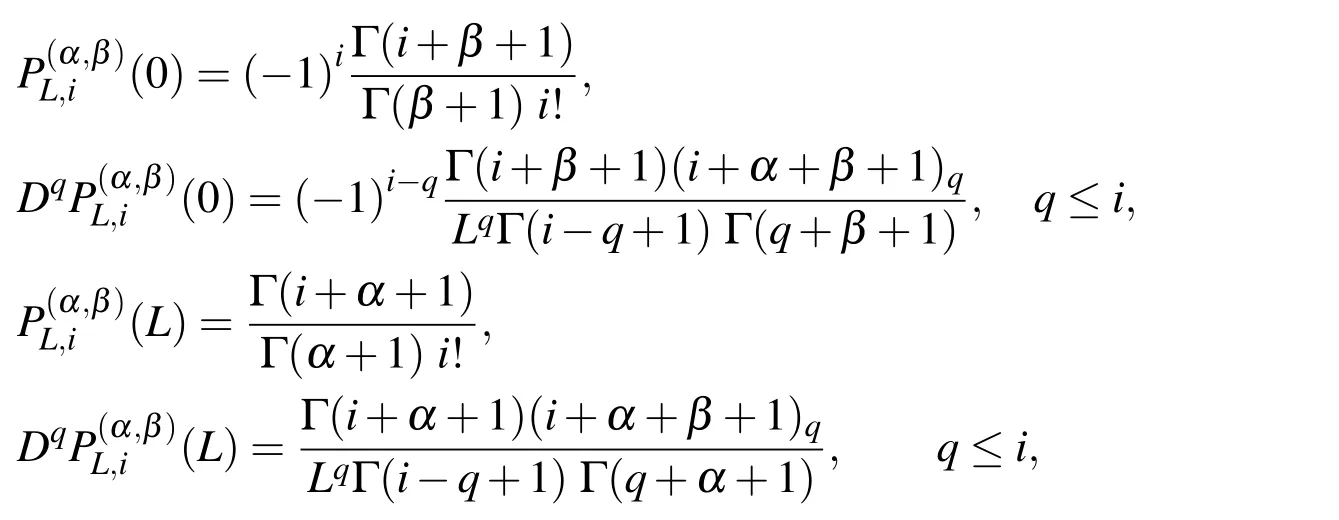
which will be of important use later.

Assume y(x)is a square integrable function with respect to the Jacobi weight functionin(0,L),then it can be expressed in terms of shifted Jacobi polynomials as

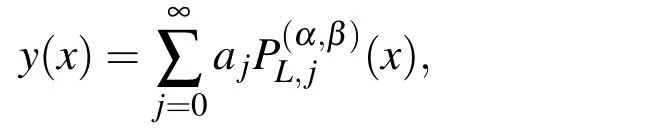
from which the coefficients ajare given by

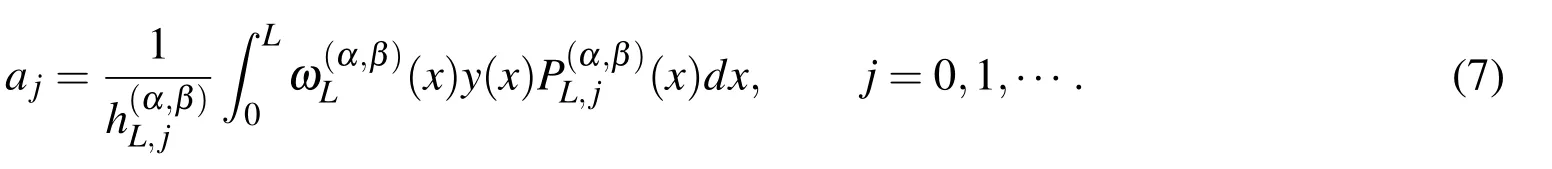
If we approximate y(x)by the first(N+1)-terms,then we can write

which alternatively may be written in the matrix form:

with

Similarly,let y(x,t)be an in finitely differentiable function defined on 0＜x≤L and 0＜t≤τ.Then it is possible to express as

with

and

The fractional differentiation of order ν of∆L,N(x)can be expressed as

whereD(ν)is the(N+1)×(N+1)Jacobi operational matrix of differentiation of order ν in the Caputo sense and is defined as follows:

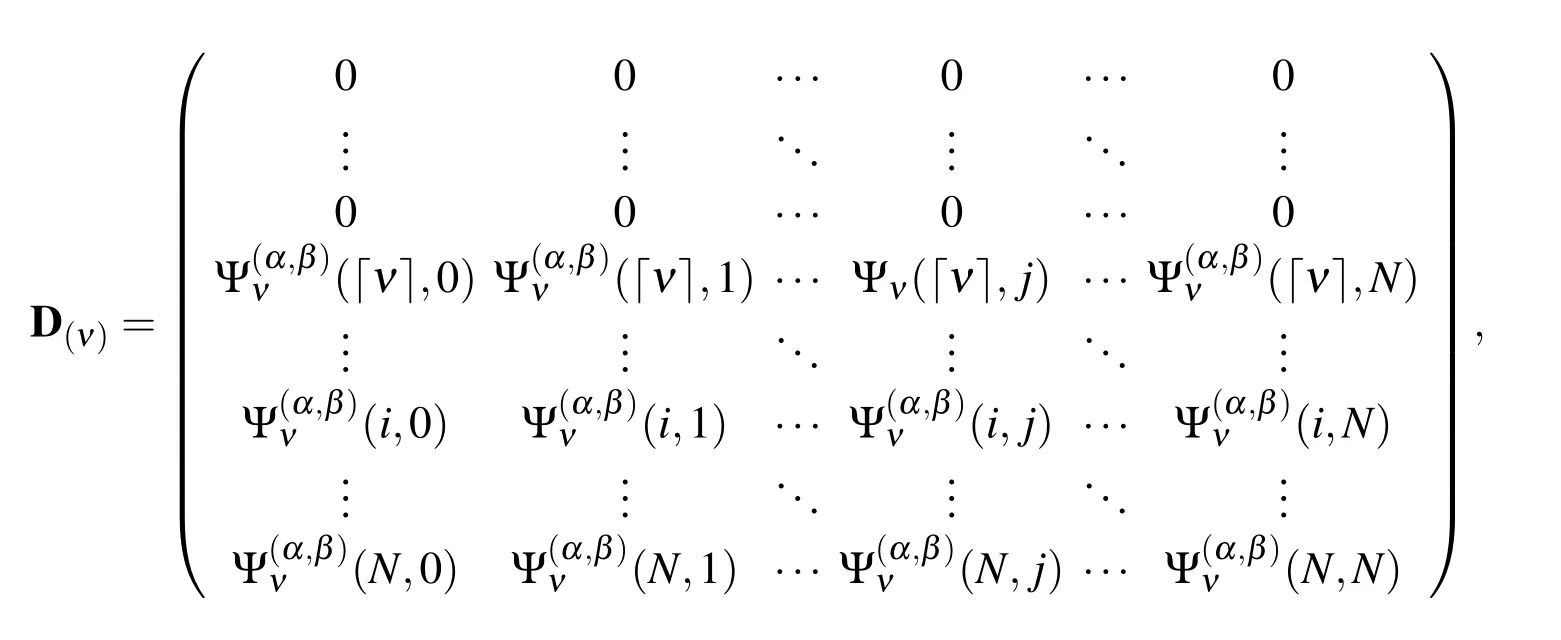
where

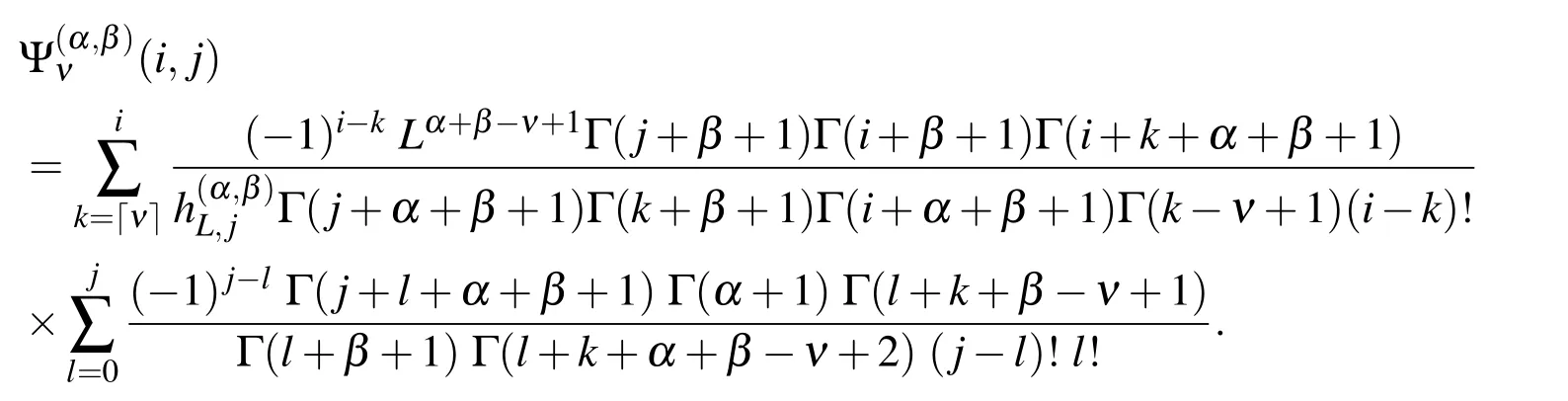
Note that inD(ν),the first■ν■rows,are all zero,(see[Doha,Bhrawy and Ezz-Eldien(2011)]for proof).

3 Time-fractional linear KdV equation

In this section,we use the operational matrix of fractional derivatives,the collocation spectral method and the Gauss quadrature formula with the shifted Jacobi polynomials as the basis functions to solve the time-fractional linear KdV equation:

with the initial condition

and boundary conditions

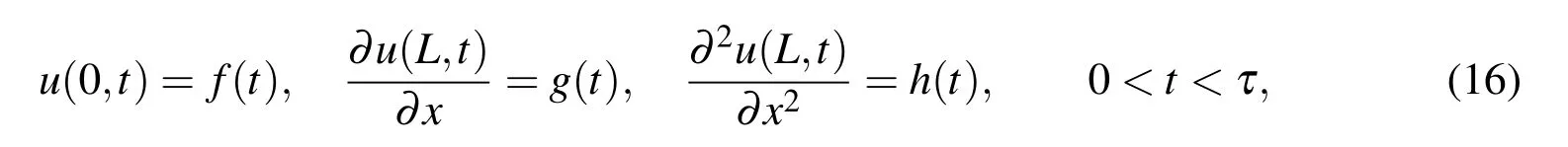
where ν,(0＜ ν ≤ 1),A,B are real constants and s(x,t)is the source function.The function u(x,t)is assumed to be the causal function of time and space,i.e.,vanishing for t＜0 and x＜0.

First,the initial-boundary value problem(14)-(16)is equivalent to the boundary value problem

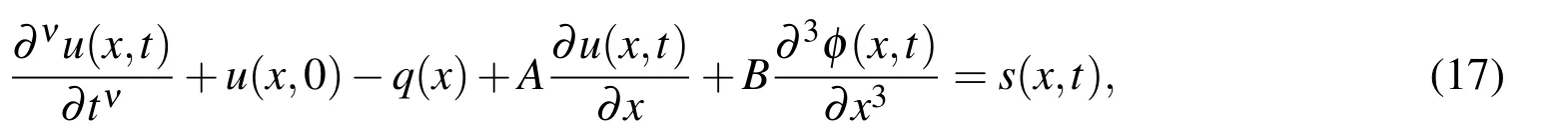
with the boundary conditions(16).

Now,we approximate u(x,t)and s(x,t)by the shifted Jacobi polynomials as

whereUis an unknown coefficients(M+1)×(N+1)matrix,whileSis a known matrix that can be written as

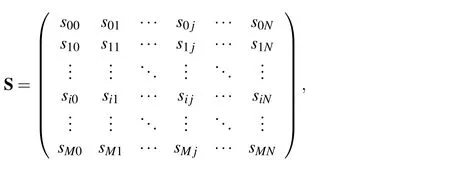
where the coefficients sij;i=0,1,···,M,j=0,1,···,N can be evaluated by

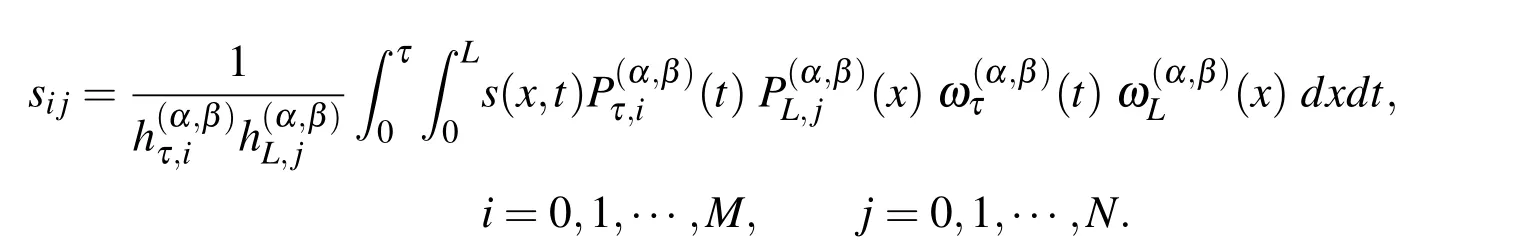
For general function s(x,t),it is more difficult to compute the previous integral exactly.Using the Jacobi-Gauss quadrature formula,we can approximate the coefficients sijas

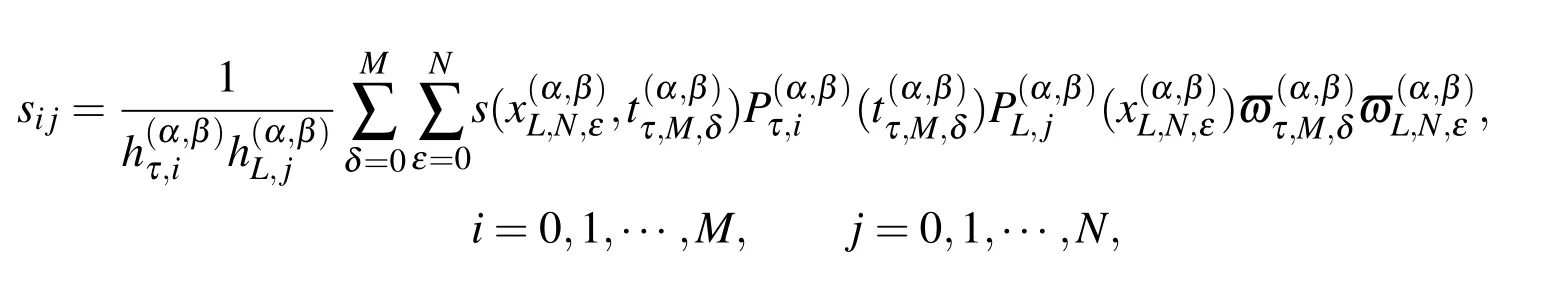
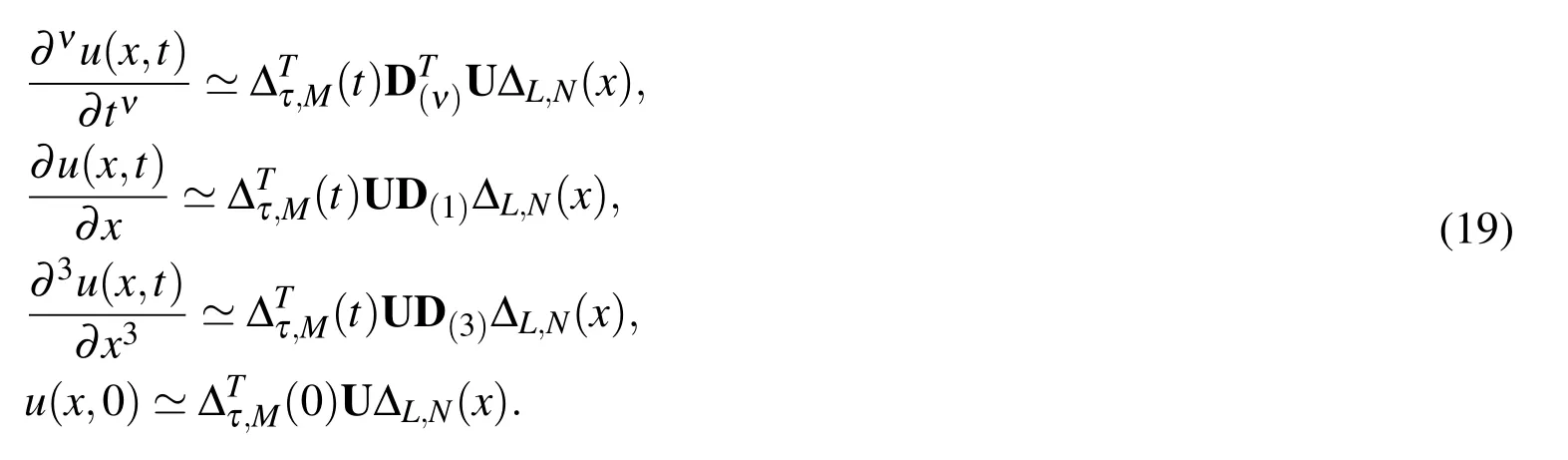
By substituting(18)and(19)in(17),we get

We collocate(20)at(M+1)(N−2)points,as

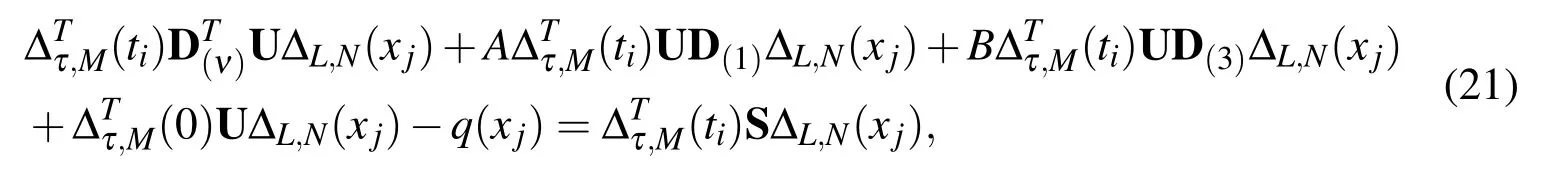
where ti,i=0,1,···,M are the roots ofwhile xj,j=0,1,···,N − 3 are the roots ofthis generates a system of(M+1)(N −2)nonlinear algebraic equations in the unknown expansion coefficients,uij,i=0,1,···,M;j=0,1,···,N −2,and the rest of this system is obtained from the boundary conditions(16),as

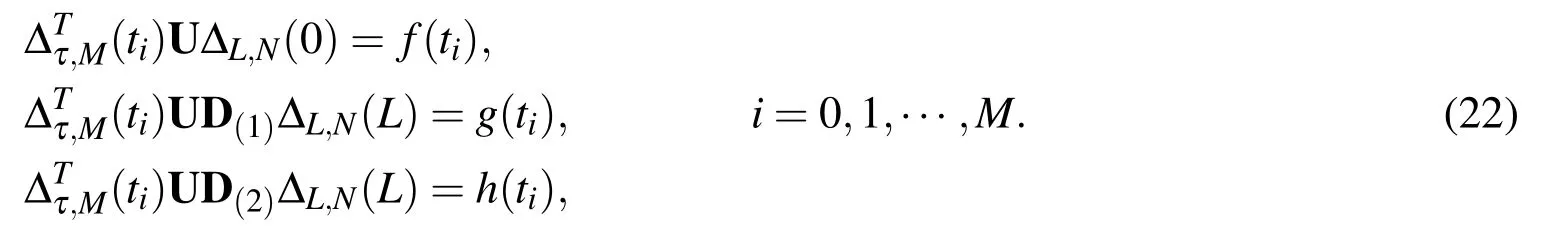
The(M+1)(N−2)system(21)may be combined with the 3(M+1)system(22)to be written as a(M+1)(N+1)system of nonlinear algebraic equations in the unknown expansion coefficients uij,that can solved using Newton’s iterative method.Consequently uM,N(x,t)given in(18)can be calculated.

4 Time-fractional nonlinear KdV equation

In this section,we apply the numerical technique obtained in the previous section to solve the time-fractional nonlinear KdV equation:

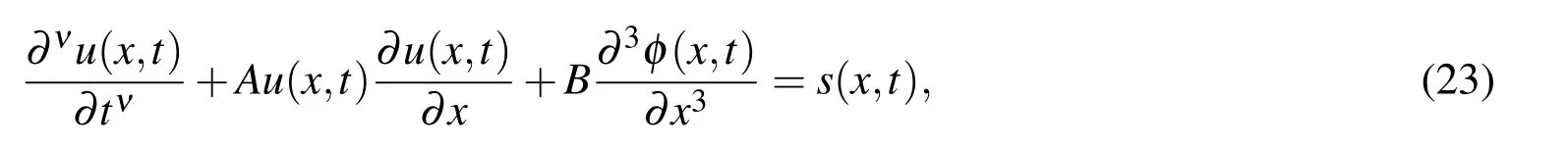
with the initial condition(15)and the boundary conditions(16).

As in the previous section,we can rewrite(23)as in the following form:

with the boundary conditions(16).

Now,we collocate Eq.(25)at(M+1)(N−2)points,as

this generates a system of(M+1)(N−2)nonlinear algebraic equations in the unknown expansion coefficients,uij,i=0,1,···,M;j=0,1,···,N − 2,and the rest of this system is obtained from the boundary conditions(16),as in Eq.(22).The(M+1)(N−2)system(26)may be combined with the 3(M+1)system(22)to be written as a(M+1)(N+1)system of nonlinear algebraic equations in the unknown expansion coefficients uij,that can solved using Newton’s iterative method.Consequently uM,N(x,t)given in(18)can be calculated.

5 Time-fractional modified KdV equation

In this section,we consider the following time-fractional modified KdV equation

with the initial condition(15)and the boundary conditions(16).

As in the previous section,Eq.(27)can be written as

with the boundary conditions(16).

Now,we collocate Eq.(29)at(M+1)(N−2)points,as

this generates a system of(M+1)(N−2)nonlinear algebraic equations in the unknown expansion coefficients,uij,i=0,1,···,M;j=0,1,···,N − 2,and the rest of this system is obtained from the boundary conditions(16),as in Eq.(22).The(M+1)(N−2)system(30)may be combined with the 3(M+1)system(22)to be written as a(M+1)(N+1)system of nonlinear algebraic equations in the unknown expansion coefficients uij,that can solved using Newton’s iterative method.Consequently uM,N(x,t)given in(18)can be calculated.

6 Numerical results

For ensuring the efficiency of the proposed numerical techniques,the numerical results of some numerical examples of the time-fractional linear,nonlinear and modified KdV equation have been introduced in this section.Also,comparisons between our results and the exact solutions of such problems are introduced.

6.1 Linear fractional KdV equation

As the first example,we consider the linear time-fractional KdV equation studied in[Momani,Odibat and Alawanh(2008)]:

with the initial condition

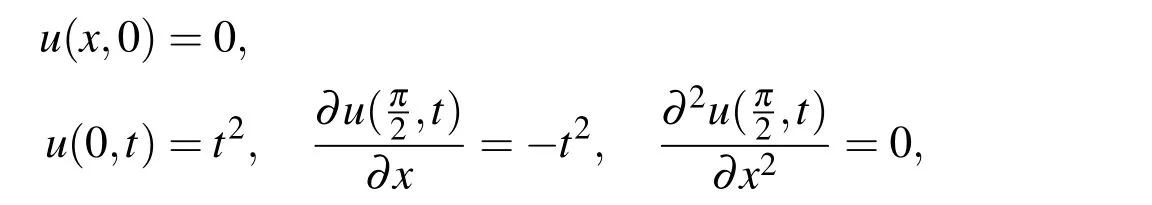
Momani et al.[Momani,Odibat and Alawanh(2008)]introduced this problem and applied the variational iteration method for introducing an approximate solution for it.In order to show the high accuracy of the numerical technique presented in Section 3,we have applied it to solve problem(31).In Table 1,we list the absolute errors atwith ν=0.50,ν=0.90 and different values of M,(M=N).Also,Figs.1-2 show the absolute error functions at α =β =0,N=M=12 with ν =0.50 and ν =0.90,respectively.

Figure 1:Absolute error function at α = β =0 with N=M=12 and ν =0.5 for problem(31).

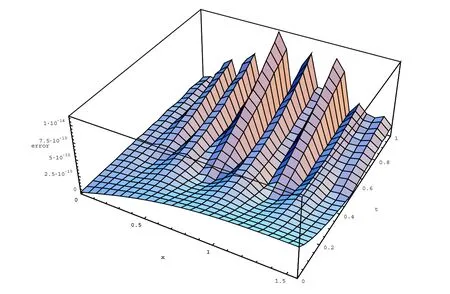
Figure 2:Absolute error function at α = β =0 with N=M=12 and ν =0.9 for problem(31).

Table 1:Absolute errors at with two different choices of ν for problem(31).

Table 1:Absolute errors at with two different choices of ν for problem(31).

6.2 Homogeneous fractional KdV equation

As the second example,we consider the nonlinear homogeneous time-fractional KdV equation[Momani(2005);Odibat and Momani(2009)]

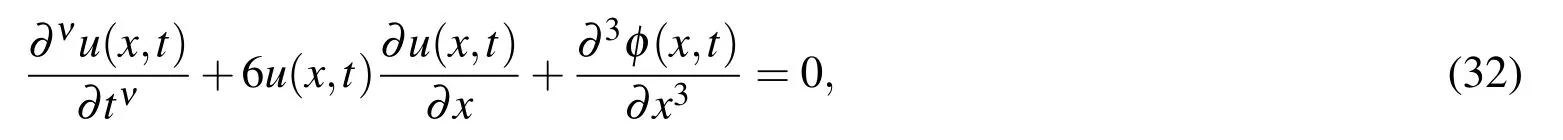
with the initial-boundary conditions

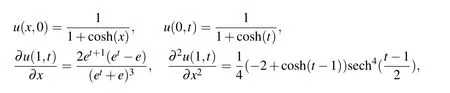
In[Momani(2005)]and[Odibat and Momani(2009)],the Adomian decomposition method and the variational iteration method have been applied respectively to approximate the solution of this problem.In Fig.3,we plot the absolute error function at α = β =0 with N=M=12 and ν =1 for problem(32),while Fig.4 present the approximate values of u(x,1)as function of space at N=10,α=β=1 and various choices of ν,ν =1,0.90,0.70,0.50 and 0.30.

From Fig.3,it is clear that adding few terms of shifted Jacobi polynomials,good approximations of the exact solution were achieved.On the other hand,Fig.4 obtain that as ν approaches to 1,the solution for the integer order system is recovered.

Figure 3:Absolute error function at α = β =0 with N=M=12 and ν =1 for problem(32).

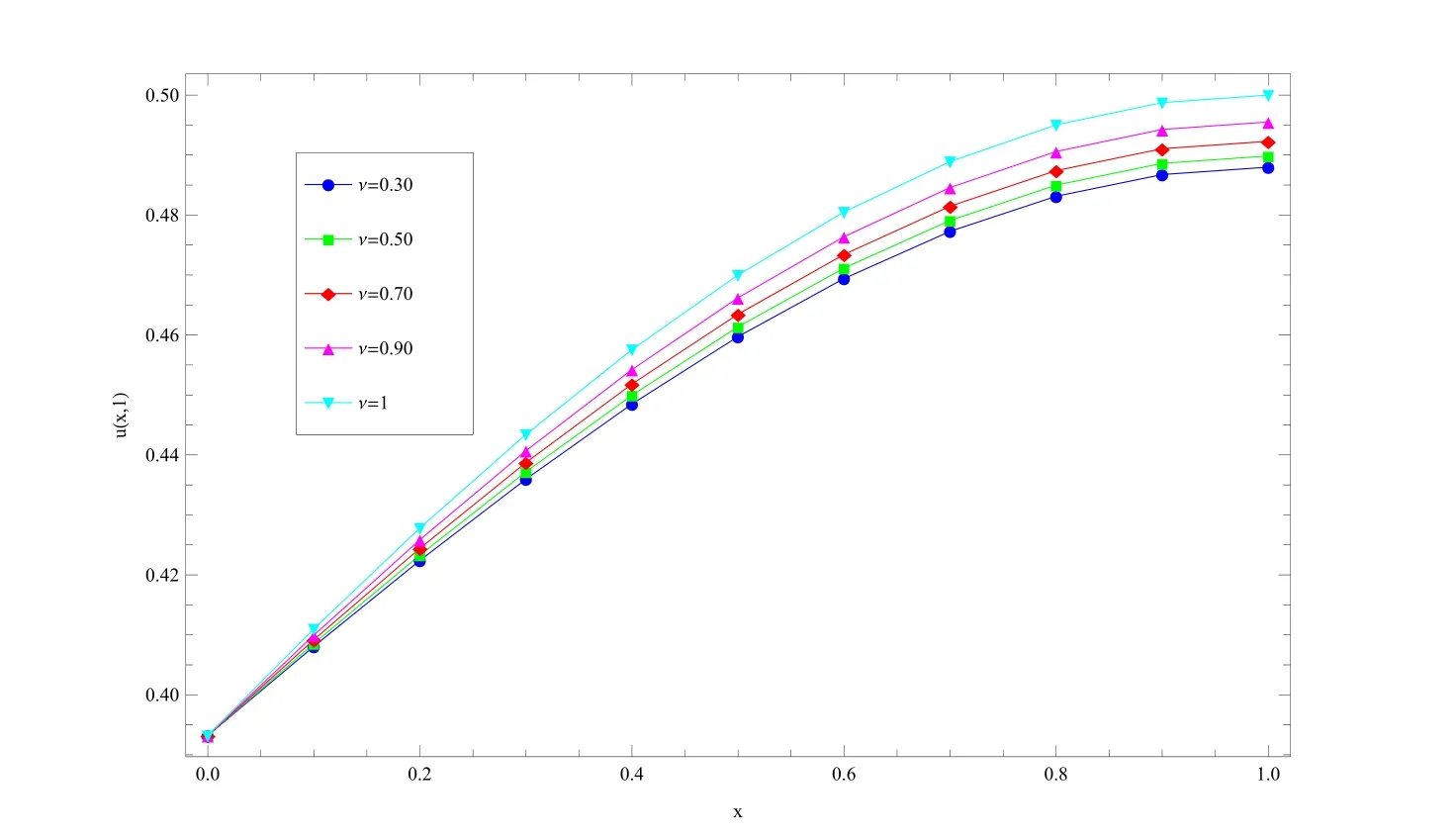
Figure 4:Approximate solution of u(x,1)at α = β =1,N=10 and ν =1,0.90,0.70,0.50 and 0.30 for Example(32).

6.3 Inhomogeneous fractional KdV equation

Consider the following inhomogeneous time-fractional KdV equation

with the initial-boundary conditions

and the exact solution u(x,t)=t3ex.

Table 2 lists the L∞and L2errors at α = β =0 and ν =0.40, ν =0.80 with different values of M,(M=N),while in Table 3,we obtain the absolute errors at α =β =1,t=1 at ν=0.40,ν=0.80 with different values of M,(M=N).Also,in Figs.5-6,we plot the absolute error functions at α =β =1,N=M=12 with ν=0.20 and ν=0.60,respectively.

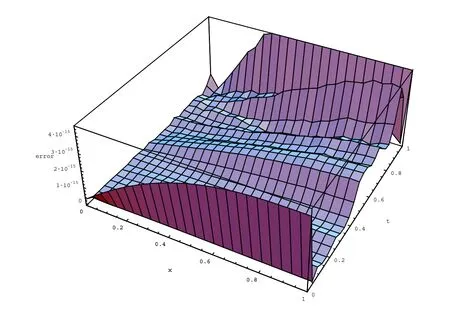
Figure 5:Absolute error function at α = β =1 with N=M=12 and ν =0.2 for problem(33).

Figure 6:Absolute error function at α = β =1 with N=M=12 and ν =0.6 for problem(33).

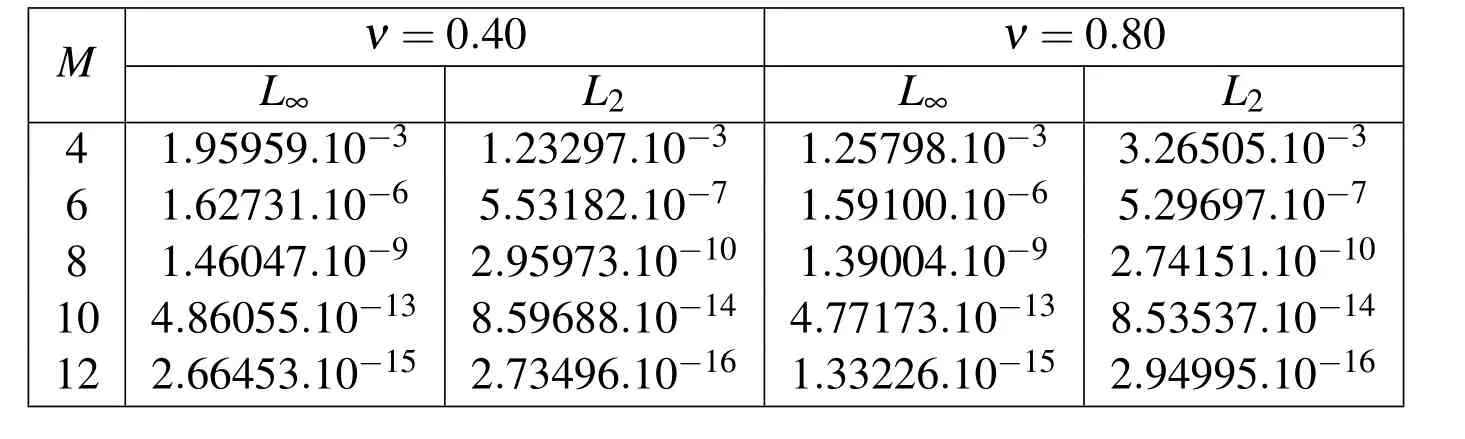
Table 2:L∞ and L2errors at α = β =0 with two different choices of ν for problem(33).

6.4 Fractional modified KdV equation

Here,we consider the fractional modified KdV equation in the form:

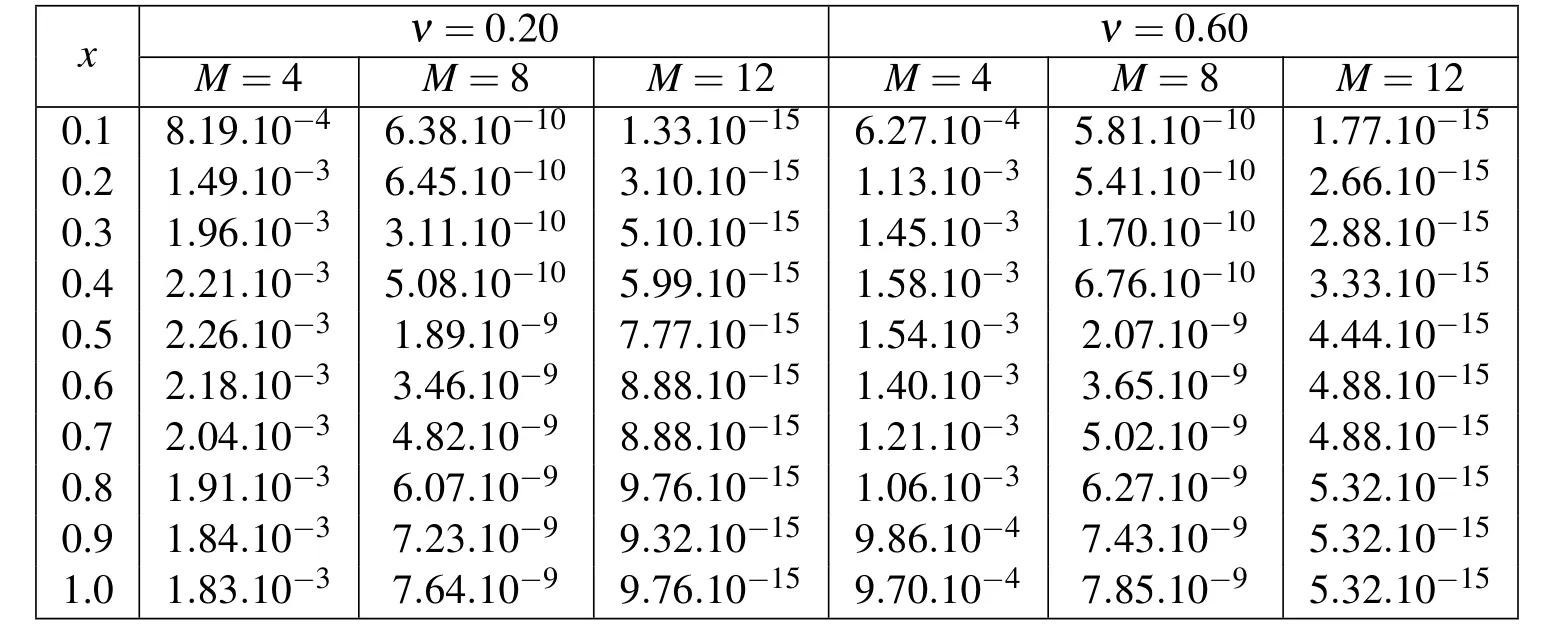
Table 3:Absolute errors at α = β =1,t=1 with two different choices of ν for problem(33).

with the initial-boundary conditions

and the exact solution u(x,t)=t2cos(x).

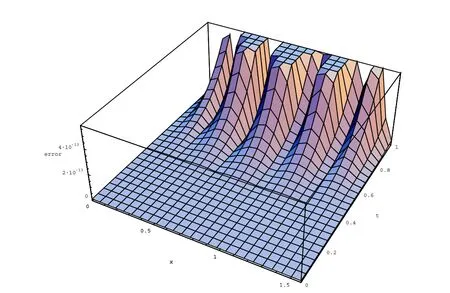
Figure 7:Absolute error function at α = β =0 with N=M=12 and ν =0.8 for problem(34).

Figure 8:Absolute error function at α = β =0 with N=M=12 and ν =0.2 for problem(34).

Figure 9:Log10MAE of u(x,t)at α =β =0 for problem(34).

This problem has been solved by using the technique discussed in Section 5.Table 4 list the maximum absolute errors(MAEs)at α =β =0 with different choices of M,(M=N)and ν .Also,Figs.7-8 plot the absolute error functions at α =β=0,N=M=12 with ν=0.20 and 0.80,respectively.Finally,in Fig.9,we plot the logarithmic graphs of the MAEs(log10Error)at two different choices of ν and various choices of M,(N=M);by using the presented algorithm.From this figures,it is shown that the numerical errors decay rapidly as M increase.

Table 4:MAEs at α = β =0 with different choices of M,(M=N)and ν for problem(34).

7 Conclusions

In the current paper,an accurate numerical technique is constructed and applied to solve the linear and nonlinear time-fractional KdV equations.The operational matrix of fractional derivatives is used together with the collocation spectral method based on the shifted Jacobi polynomials for reducing such problems into a problem consists of solving a system of algebraic equations which simplifying the problem.The fractional derivative is described in the sense of Caputo.In addition,the presented technique is applied also to solve the time-fractional modified KdV equation.The numerical results have been achieved demonstrated the high efficiency and accuracy of our techniques.Moreover,only a small number of shifted Jacobi polynomials is needed to obtain a satisfactory solution.

Abd-Elhameed,W.M.(2014):On solving linear and nonlinear sixth-order two point boundary value problems via an elegant harmonic numbers operational matrix of derivatives.CMES-Comp.Model.Eng.,vol.101,pp.159-185.

Abdelkawy,M.A.;Zaky,M.A.;Bhrawy,A.H.;Baleanu,D.(2015):Numerical simulation of time variable fractional order mobile-immobile advection-dispersion model.Rom.Rep.Phys.,vol.67,no.3.

Abdulaziz,O.;Hashim,I.;Ismail,E.S.(2009):Approximate analytical solution to fractional modified KdV equations.Math.Comput.Model.,vol.49,pp.136-145.

Alcoutlabi,M.;Martinez-Vega,J.J.(1998):Application of fractional calculus to vixcoelastic behavior modelling and to the physical ageing phenomena in glassy amorphous polymers.Polymer,vol.39,pp.6269-6277.

Al-Khaled,K.(2015):Numerical solution of time-fractional partial differential equations using sumudu decomposition method.Rom.J.Phys.,vol.60,pp.99-110.

Avila;R.Ramos;E.;Atluri,S.N.(2009):The Chebyshev tau spectral method for the solution of the linear stability equations for Rayleigh-Benard convection with melting.CMES-Comp.Model.Eng.,vol.51,pp.73-92.

Bhrawy,A.H.;Abdelkawy,M.A.(2015):A fully spectral collocation approximation for multi-dimensional fractional Schrodinger equations.J.Comput.Phys.,vol.294,pp.462-483.

Bhrawy,A.H.;Alghamdi,M.M.;Taha,T.M.(2012):A new modified generalized Laguerre operational matrix of fractional integration for solving fractional differential equations on the half line.Advances in Difference Equations,vol.2012,pp.1-12.

Bhrawy,A.H.;Alo fi,A.S.(2013):The operational matrix of fractional integration for shifted Chebyshev polynomials.Appl.Math.Lett.,vol.26,pp.25-31.

Bhrawy,A.H.;Doha,E.H.;Baleanu,D.;Ezz-Eldien,S.S.;Abdelkawy,M.A.(2015):An accurate numerical technique for solving fractional optimal control problems.Proc.Romanian Acad.A,vol.16,pp.47-54.

Bhrawy,A.H.;Zaky,M.A.(2015a):A method based on the Jacobi tau approximation for solving multi-term time-space fractional partial differential equations.J.Comput.Phys.,vol.281 pp.876-895.

Bhrawy,A.H.;Zaky,M.A.(2015b):Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation.Nonlinear Dynam.,vol.80,pp.101-116.

Biswas,A.;Bhrawy,A.H.;Abdelkawy,M.A.;Alshaery,A.A.;Hilal,E.M.(2014):Symbolic computation of some nonlinear fractional differential equations.Rom.J.Phys.,vol.59,pp.433-442.

Chen,Y.;Han,X.;Liu,L.(2014):Numerical solution for a class of linear system of fractional differential equations by the HaarWavelet method and the convergence analysis.CMES-Comp.Model.Eng.,vol.97,pp.391-405.

Chen,Y.;Liu,L.;Li,X.;Sun,Y.(2014):Numerical solution for the variable order time fractional diffusion equation with Bernstein polynomials.CMES-Comp.Model.Eng.,vol.97 pp.81-100.

Dehghan,M.;Abbaszadeh,M.;Mohebbi,A.(2015a):An implicit RBF meshless approach for solving the time fractional nonlinear sine-Gordon and Klein-Gordon equations.Eng.Anal.Boundary Elem.,vol.50,pp.412-434.

Dehghan,M.;Abbaszadeh,M.;Mohebbi,A.(2015b):Error estimate for the numerical solution of fractional reaction-subdiffusion process based on a meshless method.J.Computa.Appl.Math.,vol.280,pp.14-36.

Doha,E.H.;Abd-Elhameed,W.M.;Bassuony,M.A.(2015):On using third and fourth kinds Chebyshev operational matrices for solving Lane-Emden type equations.Rom.J.Phys.vol.60,no.3-4.

Doha,E.H.;Bhrawy,A.H.;Ezz-Eldien,S.S.(2011):A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order.Comput.Math.Appl.,vol.62,pp.2364-2373.

Doha,E.H.;Bhrawy,A.H.;Ezz-Eldien,S.S.(2012):A new Jacobi operational matrix:An application for solving fractional differential equations.Appl.Math.Model.,vol.36,pp.4931-4943.

Doha,E.H.;Bhrawy,A.H.;Ezz-Eldien,S.S.(2015):An efficient Legendre spectral tau matrix formulation for solving fractional sub-diffusion and reaction sub-diffusion equations.J.Comput.Nonlinear Dyn.,vol.10,pp.021019.

Dou,F.F.;Hon,Y.C.(2014):Numerical computation for backward time-fractional diffusion equation.Eng.Anal.Boundary Elem.,vol.40,pp.138-146.

El-Danaf,T.S.;Hadhoud,A.R.(2012):Parametric spline functions for the solution of the one time fractional Burgers’equation.Appl.Math.Modell.,vol.36,pp.4557-4564.

El-Wakil,S.A.;Abulwafa,E.M.;Zahran,M.A.;Mahmoud,A.A.(2011):Time-fractional KdV equation:formulation and solution using variational methods.Nonlinear Dyn.,vol.65,pp.55-63.

Garrappa,R.(2015):Trapezoidal methods for fractional differential equations:Theoretical and computational aspects.Mathematics and Computers in Simulation,vol.110,pp.96-112.

Garrappa,R.;Popolizio,M.(2011):On accurate product integration rules for linear fractional differential equations.J.Comput.Appl.Math.,vol.235,pp.1085-1097.

Gao,Y.T.;Tian,B.(2001):Ion-acoustic shocks in space and laboratory dusty plasmas:Two-dimensional and non-traveling-wave observable effects.Phys Plasmas,vol.8,pp.3146.

Gulsu,M.;Ozturk,Y.;Anapal,A.(2013):Numerical approach for solving fractional relaxation-oscillation equation.Appl.Math.Modell.,vol.37,pp.5927-5937.

Guo,S.;Mei,L.;Fang,Y.;Qiu,Z.(2012):Compacton and solitary pattern solutions for nonlinear dispersive KdV-type equations involving Jumarie’s fractional derivative.Physics Letters A,vol.376,pp.158-164.

Hwang,C.;Geubelle,P.H.(2000):A spectral scheme to simulate dynamic fracture problems in composites.CMES-Comp.Model.Eng.,vol.4,pp.45-56.

Jiang,Y.L.;Ding,X.L.(2013):Waveform relaxation methods for fractional differential equations with the Caputo derivatives.J.Comput.Appl.Math.,vol.238,pp.51-67.

Karpman,V.I.(1998):Radiation by weakly nonlinear shallow-water solitons due to higher-order dispersion.Phys.Rev.E,vol.58,pp.5070.

Kumar,D.;Singh,J.;Kumar,S.(2015):A fractional model of Navier-Stokes equation arising in unsteady flow of a viscous fluid.Journal of the Association of Arab Universities for Basic and Applied Sciences,vol.17,pp.14-19.

Kumar,D.;Singh,J.;Sushila(2013):Application of homotopy analysis transform method of fractional biological population model.Rom.Rep.Phys.,vol 65,pp.63-75.

Kurulay,M.;Bayram,M.(2010):Approximate analytical solution for the fractional modified KdV by differential transform method.Commun.Nonlinear Sci.Numer.Simulat.,vol.15,pp.1777-1782.

Leblond,H.;Sanchez,F.(2003):Models for optical solitons in the two-cycle regime.Phys.Rev.E,vol.67,pp.013804.

Li,C.;Chen,A.;Ye,J.(2011):Numerical approaches to fractional calculus and fractional ordinary differential equation.J.Comput.Phys.,vol.230,pp.3352-3368.

Li,B.(2014):Numerical solution of fractional Fredholm-Volterra integro-differential equations by means of generalized Hat functions method.CMES-Comp.Model.Eng.,vol.99,pp.105-122.

Lin,Z.;Wang,J.;Wei,W.(2015):Multipoint BVPs for generalized impulsive fractional differential equations.Appl.Math.Comput.,vol.258,pp.608-616.

Liu,Z.Z.;Zhou,X.J.;Liu,X.M.;Luo,J.(2003):Density waves in traffic flow of two kinds of vehicles.Phys.Rev.E,vol.67,pp.017601.

Momani,S.(2005):An explicit and numerical solutions of the fractional KdV equation.Math.Comput.Simul.,vol.70,pp.110-118.

Momani,S.;Odibat,Z.;Alawnah,A.(2008):Variational iteration method for solving the space-and time-fractional KdV equation.Numer.Methods Partial Differ.Equ.,vol.24,pp.261-271.

Odibat,Z.;Momani,S.(2009):The variational iteration method:An efficient scheme for handling fractional partial differential equations in fluid mechanics.Comput.Math.Appl.,vol.58,pp.2199-2208.

Pang,G.;Chen,W.;Sze,K.Y.(2014):Differential quadrature and cubature methods for steady-state space-fractional advection-diffusion equations.CMESComp.Model.Eng.,vol.97,pp.299-322.

Ray,S.S.(2012):On Haar wavelet operational matrix of general order and its application for the numerical solution of fractional Bagley Torvik equation.Appl.Math.Comput.,vol.218,pp.5239-5248.

Saadatmandi,A.;Dehghan,M.(2010):A new operational matrix for solving fractional-order differential equations.Comput.Math.Appl.,vol.59,pp.1326-1336.

Saadatmandi,A.;Dehghan,M.(2011):A tau approach for solution of the space fractional diffusion equation.Comput.Math.Appl.,vol.62,pp.1135-1142.

Sadati,S.J.;Ghaderi,R.;Ranjbar,A.N.(2013):Some fractional comparison results and stability theorem for fractional time delay systems.Rom.Rep.Phys.vol.65,pp.94-102.

Shukla,H.S.;Tamsir,M.;Srivastava,V.K.;Kumar,J.(2014):Approximate analytical solution of time-fractional order Cauchy-reaction diffusion equation.CMES-Comp.Model.Eng.,vol.103,pp.1-17.

Valipour,E.;Yaghoobi,M.A.;Mashinchi,M.(2014):An iterative approach to solve multiobjective linear fractional programming problems.Appl.Math.Modell.,vol.38,pp.38-49.

Wang,Q.(2007):Homotopy perturbation method for fractional KdV equation.Appl.Math.Comput.,vol.190,pp.1795-1802.

Wang,H.;Du,N.(2014):Fast alternating-direction finite difference methods for three-dimensional space-fractional diffusion equations.J.Comput.Phys.,vol.258,pp.305-318.

Wang,Y.;Du,M.;Tan,F.;Li,Z.;Nie,T.(2013):Using reproducing kernel for solving a class of fractional partial differential equation with non-classical conditions.Appl.Math.Comput.,vol.219,pp.5918-5925.

Wang,J.;Liu,L.;Chen,Y.;Liu,L.;Liu,D.(2014):Numerical study for a class of variable order fractional integral-differential equation in terms of Bernstein polynomials.CMES-Comp.Model.Eng.,vol.105,pp.69-85.

Wang,G.W.;Xu,T.Z.(2014a):The improved fractional sub-equation method and its applications to nonlinear fractional partial differential equations.Rom.Rep.Phys.,vol.66,pp.595-602.

Wang,G.W.;Xu,T.Z.(2014b):The modified fractional sub-equation method and its applications to nonlinear fractional partial differential equations.Rom.J.Phys.,vol.66,pp.636-645.

Wei,H.;Chen,W.;Sun,H.(2014):Homotopy method for parameter determination of solute transport with fractional advection-dispersion equation.CMESComp.Model.Eng.,vol.100,pp.85-103.

Wei,M.B.;Zeng,D.Q.(2012):Fractional perturpation technique of fractional differentiable functions.Rom.J.Phys.,vol.57,pp.1278-1284.

Yu,Q.;Liu,F.;Turner,I.;Burrage,K.(2014):Numerical simulation of the fractional Bloch equations.J.Comput.Appl.Math.,vol.255,pp.635-651.

1Department of Mathematics,Faculty of Science,King Abdulaziz University,Jeddah,Saudi Arabia.

2Department of Mathematics,Faculty of Science,Beni-Suef University,Beni-Suef,Egypt.

3Department of Mathematics,Faculty of Science,Cairo University,Giza,Egypt.

4Department of Mathematics,Faculty of Science,Assiut University,New Valley Branch,El-Kharja 72511,Egypt.