表面凹槽形态对Q-P-T钢成形能力预测的影响

龚俊杰，郝庆国，左训伟，郭正洪，陈乃录，戎咏华

（上海交通大学材料科学与工程学院，上海200240）

0 引 言

徐祖耀［1］提出的淬火-分配-回火（Q-P-T）新型热处理工艺不仅可使中碳铁-锰-硅-铌马氏体钢的强塑积达到30 000MPa·%，且远远超过了目前先进高强钢强塑积的极限值（25 000MPa·%），而且还可使低碳 Q-P-T钢的强塑积超过20 000MPa·%［2］。与通常的淬火-回火（调质）工艺相比，经Q-P-T工艺处理的马氏体钢可获得更多的残余奥氏体（体积分数通常大于10%），故呈现出较高的强度和塑性［2］。研究人员对Q-P-T钢的微观组织和力学性能进行了大量研究［2-4］，但对其成形性能的研究还很少。

成形极限图（FLD）是目前应用最为广泛的描述材料成形特征的工具，它描述了板材在成形加工时最大的许可应变。通常，确定FLD的方法有试验和理论计算两种，其中前者不仅工作量大，而且得到的数据往往很分散以至于FLD的准确性受到影响，因此数值计算方法被广泛用于FLD的预测。数值计算方法通常是基于不同的屈服准则和塑性本构关系，然后以不同的拉伸失稳准则作为颈缩和断裂的条件进行解析得到极限应变。

著名的成形极限理论有Swift［5］提出的分散性失稳理论和Hill［6］提出的集中性失稳理论，它们为塑性变形拉伸失稳理论奠定了基础。目前应用最广泛的失稳理论是基于 Marciniak和Kuczynski［7］提出的M-K凹槽理论，其中凹槽的深度表征厚度的不均匀性和缺陷的大小，凹槽与表面的倾斜角度表征凹槽与拉伸轴的位向。近年来，国内外对M-K理论模型进行了大量研究及改进，Zhou和Neale［8］等结合M-K模型和晶体塑性变形理论对退火后面心立方（FCC）板材的成形性进行了预测，但他们的模型中未考虑弹性因素，而且认为凹槽始终与主应力方向垂直；Asaro和Needleman［9］计算了等双轴拉伸下板材的应变极限；Wu［10］等应用Asaro和Needleman［9］的多晶体塑性模型计算出了FCC多晶体板材的成形极限，其中引入了凹槽与拉伸轴的角度随应变增加而逐渐变化的假设。然而，多大的凹槽角度才能与实际情况相符尚未给出结论，因此有必要进一步进行深入研究。此外，前期的理论研究虽然考虑了初始厚度不均度对成形性的影响，但是并未明确给出多大的凹槽深度满足成形性条件。因此作者将采取试验的方法探索凹槽深度和角度对成形性的影响。

虽然M-K理论在不断得到修正和完善，但理论预测值和试验结果仍存在一定差距；而且目前的数值模拟仍存在着诸多不足，最突出的就是缺乏综合考虑各个参数的有效方法。比如，理论预测的FLD对初始厚度不均度等参数比较敏感，容易导致FLD出现偏差；又如数值模拟方法无法完全模拟材料的真实特性，很多内部缺陷或者热处理参数均会影响材料的本构关系，而FLD的理论预测恰恰是本构关系和失稳理论相结合得出的，因此需要尽可能准确地确定本构关系。

基于上述分析，作者以Q-P-T钢为试样，首先通过试验揭示了凹槽与拉伸轴的角度（简称凹槽角度）及凹槽深度比（简称凹槽形态）对其力学性能的影响规律，为正确使用各种理论模型提供借鉴；在此基础上，结合Q-P-T钢的试验参数，预测单轴拉伸条件下的极限应变，并通过各种本构模型计算的应变值与经验曲线比较来确定M-K模型中合理的凹槽角度和凹槽深度比。鉴于FLD的预测通常只需计算三个典型值，即纵坐标上的平面极限应变、纵坐标左侧的单轴拉伸极限应变和右侧的等双轴极限应变；而且三种极限应变的计算方法是相同的，只是描述应变的公式不同。因此，作者选择单轴拉伸条件下的极限应变进行计算。

1 试样制备与试验方法

试验用钢在北京钢铁研究总院50kg中频真空感应炉中熔炼，铸锭热锻成40mm厚的板坯后再经6道热轧得到12.5mm厚的板材。其中热轧的初始温度为1 200℃，终轧温度为850℃。试验所需试样均取自母材心部，并沿轧制方向切割，以保证成分及组织的均匀性，切割得到的试样厚度为2mm。试验钢的化学成分见表1。

表1 试验钢的化学成分 （质量分数）Tab.1 Chemical composition of experimental steel（mass） %

首先根据GB／T 228-2002《金属材料室温拉伸试验方法》［11］加工出如图1所示的拉伸试样，然后对其进行Q-P-T工艺处理［2］：先在950℃奥氏体化300s，然后盐浴淬火至320℃并停留15s，随后在450℃的盐浴炉中等温30s（碳分配和回火处理），最后水淬至室温。热处理完成后，对拉伸试样进行凹槽切割，凹槽形态分为不同凹槽深度比和不同凹槽角度的组合，凹槽形态组合列于表2中，其中凹槽深度比（t为凹槽内厚度；t为凹槽外0厚度，即试样厚度，t0＝1.4mm）；凹槽与拉伸轴之间的角度称为凹槽角度。凹槽处理后的拉伸试样截面如图2所示。使用丙酮溶液清洗试样表面后，在Zwick／Roell型拉伸试验机上进行室温拉伸试验，试样标距为25mm，拉伸速度为0.5mm·min-1。

图1 拉伸试样的尺寸Fig.1 Size of tensile sample

2 试验结果与讨论

2.1 凹槽形态对力学性能的影响

由图3可见，对于同一凹槽深度比的试样，随着凹槽角度减小，试样的塑性逐渐增加，即45°凹槽试样的塑性最佳，60°凹槽的其次，90°凹槽的最差，而且它们均远低于无凹槽试样的塑性。由图4可知，不同凹槽角度下，随着凹槽深度比变小，试样的塑性都会改善，但仍远低于无凹槽试样的塑性。此外，凹槽深度比和凹槽角度对材料的应变硬化指数几乎均无影响。当凹槽角度一定时，随着凹槽深度比增加，材料的强度逐渐降低，而且降低幅度随凹槽深度比增大而增大。值得指出的是，当凹槽深度比较小时，凹槽角度的变化对试样屈服强度基本无影响，但是当凹槽深度比较大时，凹槽角度的变化会对试样屈服强度产生显著影响，其中45°凹槽试样具有最高的强度。上述现象可从式（1）得到解释。设单轴拉伸力为F，凹槽角度为θ，则作用于凹槽处的正应力σ为：

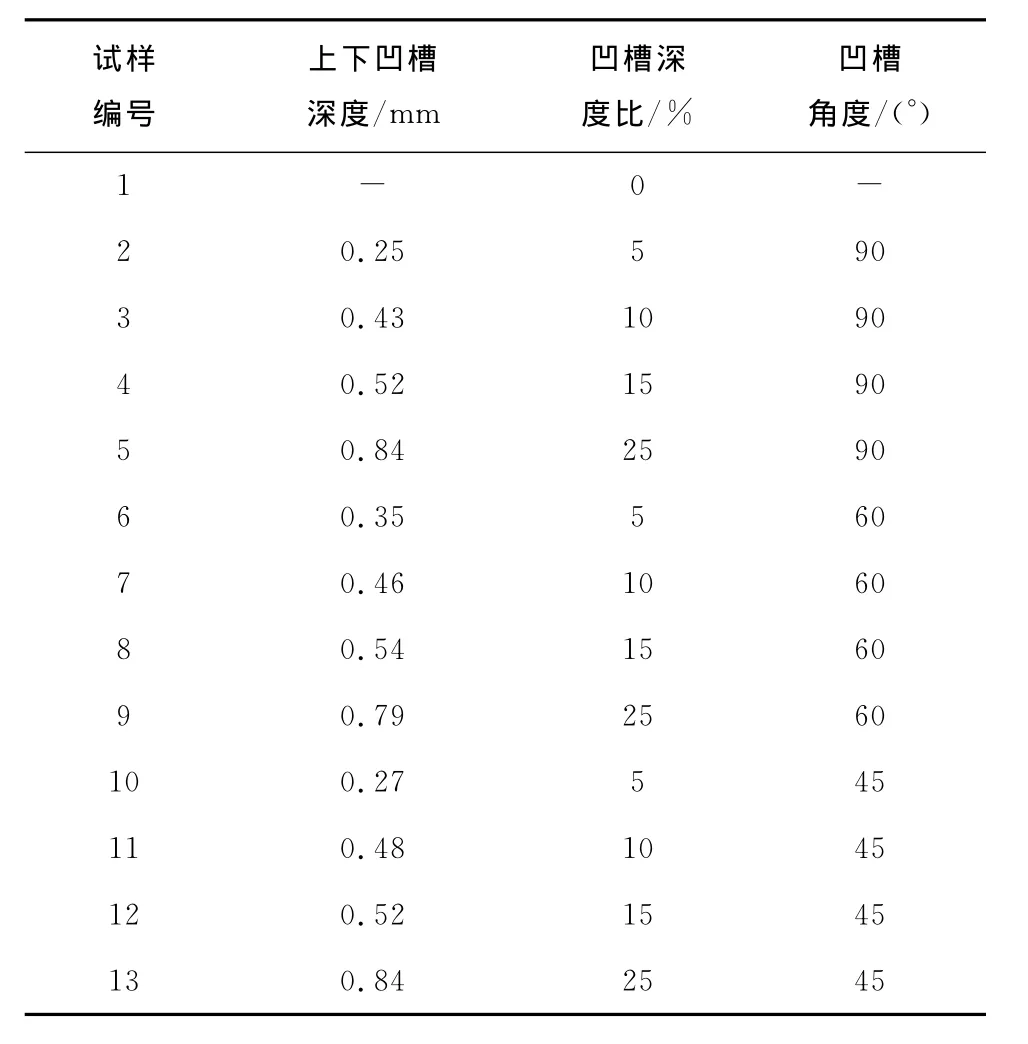
表2 不同凹槽深度比和不同凹槽角度的组合Tab.2 Combinations of different groove depth ratios and different groove angles

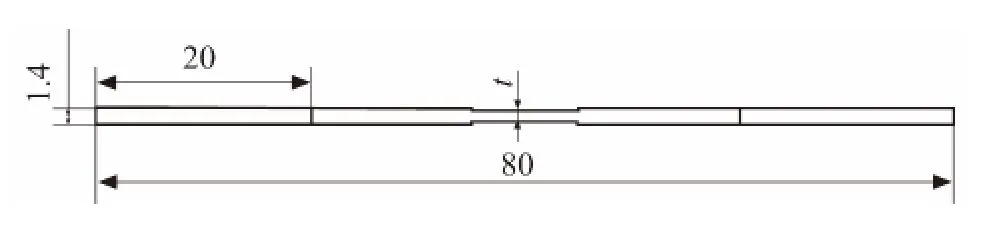
图2 90°凹槽试样侧面的示意Fig.2 Side view of specimen with 90°groove

式中：A为凹槽倾斜截面积。

当θ＝90°时，正应力为F／A，凹槽承受了最大的正应力；当θ＝0°时，正应力为零，即无正应力作用于凹槽缺陷处，因此0°凹槽几乎与无缺陷试样相同。通过式（1）可知，对于具有一定凹槽深度比的试样，随着凹槽角度减小，作用于凹槽处的正应力就越小，故其塑性越大。对于图（4）中的现象可解释为，对于一定角度的凹槽试样，随着凹槽深度比的增加，凹槽处的垂直截面积减小，但拉伸曲线上的应力是拉伸力F除以试样原始垂直截面积A0得到的，A0大于凹槽的实际受力面积，并且随凹槽深度比增大，实际的受力面积减小，故图4中的拉伸应力随凹槽深度比增加而降低。值得说明的是，在图3（d）中，60°凹槽试样的塑性几乎与90°凹槽试样的相等，且后者略高于前者的，该现象违背上述规律，其原因在于凹槽深度比超过临界值后，试样在拉伸过程中会更快地进入失稳伸长以及断裂阶段，数据波动也更为敏感，数据波动产生的误差导致产生了反常规律。

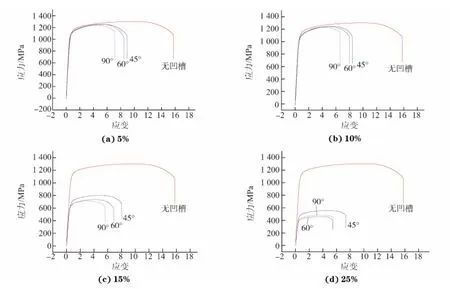
图3 不同凹槽深度比条件下凹槽角度对试验钢拉伸性能的影响Fig.3 Effect of groove angles on tensile properties of experimental steels with different groove depth ratios

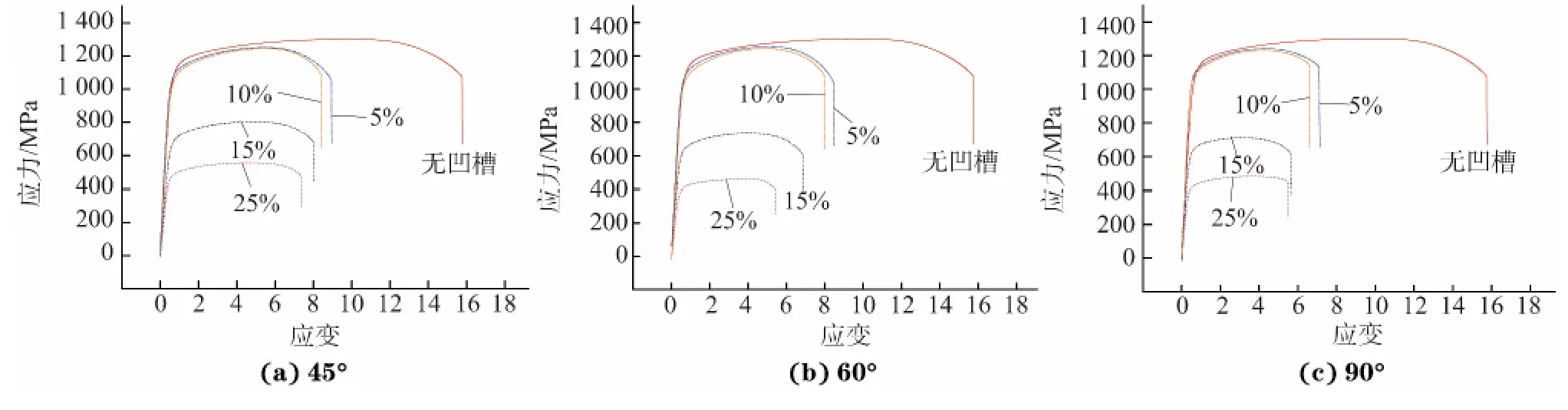
图4 不同凹槽角度条件下凹槽深度比对试验钢拉伸性能的影响Fig.4 Effect of groove depth ratios on tensile properties of experimental steel with different groove angles

2.2 本构关系拟合

作者研究关注材料的均匀塑性变形阶段。目前有很多拟合流变应力曲线的方法，如最常用的幂律Hollomon模型、Swift模型、Ludwik模型和Ghosh模型等［12］。鉴于Ghosh模型是纯数学模拟，没有物理意义，故主要选择在Hollomon模型基础上得到的Ludwik模型以及Hockett-Sherby模型对本构关系进行拟合。

Ludwik模型是非饱和外推模型，直接对屈服之后的均匀塑性变形阶段的曲线进行拟合。虽然在曲线拟合后期会开始发散，但其表现了材料塑性阶段的流变应力曲线特征，其公式为［12］：

式中：A为拟合参数，A＞0；n为应变硬化指数；εp为塑性应变；σy为屈服强度。

Hockett-Sherby（H-S）模型为饱和外推模型，保证了函数的收敛性，也反映了材料塑性变形阶段的流变应力曲线特征，其公式为［13］：

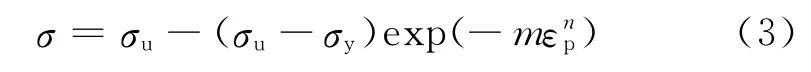
式中：m为拟合参数；σu为抗拉强度。

选取具有45°凹槽试样的数据分别采用Ludwik模型和H-S模型对塑性变形阶段进行拟合分析及对比，这是因为在试验中具有45°凹槽试样的力学性能在所有凹槽试样中是最佳的。从图5可知，采用Ludwik模型进行拟合时，曲线约在颈缩阶段开始发散，但包含了几乎全部的均匀塑性形变特征，而且其物理意义明确，即包含了屈服强度以及应变硬化指数。不同凹槽形态试样的各曲线变化规律相似，采用H-S模型拟合时，曲线最终收敛至极限强度，误差较小，同样也具有明确的物理意义。Ludwik和H-S模型适用于具有不同硬化指数的材料。

2.3 本构关系对FLD的影响

材料的本构关系是计算FLD中极限应变的重要方程，因此本构关系不同必然会导致成形性预测结果的不同。在上述试验的基础上以及对应力-应变曲线进行拟合后，以下将利用Swift-Hill模型理论预测单轴拉伸条件下的极限应变值。在Swift-Hill模型中［5-6］，假设α＝σ2／σ1（σ1为主应力，σ2为次应力），则理论公式为：

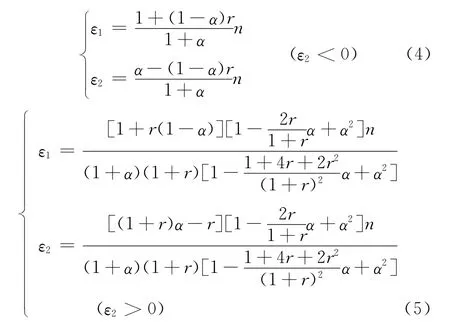
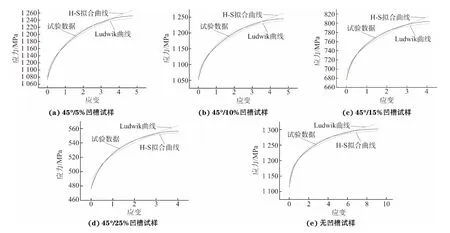
图5 凹槽试样和无凹槽试样的本构关系拟合曲线Fig.5 Constitutive relation fitted curves of specimens with and without groove：（a）specimen with groove angle of 45°and groove depth ratios of 5%；（b）specimen with groove angle of 45°and groove depth ratios of 10%；（c）specimen with groove angle of 45°and groove depth ratios of 15%；（d）specimen with groove angle of 45°and groove depth ratios of 25%and（e）specimen without groove

式中：ε1为主应变；ε2为次应变；r为塑性应变比，它的平均值rm是薄板厚度方向的各向异性度量，rm＝1表示薄板层面内的流变强度与板厚方向上的流变强度相同，rm＞1表示薄板层面内的流变强度低于板厚方向的流变强度，rm＜1表示薄板层面内的流变强度高于板厚方向的流变强度。

为了确定Ludmik模型和H-S模型哪个更适合研究Q-P-T钢，通过两个模型分别计算出45°凹槽试样和无凹槽试样在单轴拉伸条件下的极限应变，并与公认的NADDRG经验模型［14］获得的极限应变值进行比较，如图6所示。在图6的计算中，所用的参数如表3所示。基于试样的厚度波动甚是微小，故凹槽深度比取最小值，即在图6中的计算中取5%。

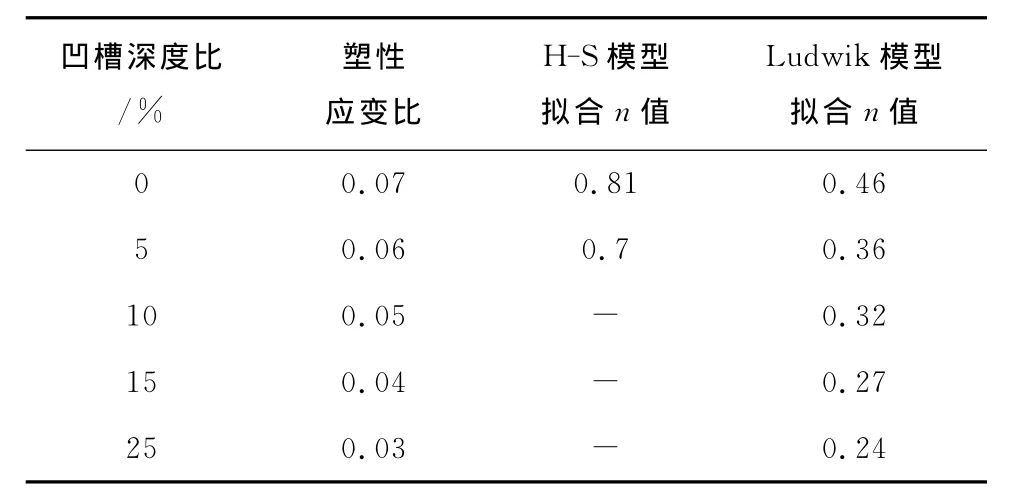
表3 极限应变计算时的相关参数值Tab.3 Parameters used in the stain limit prediction

由图6可以看出，无论是45°凹槽试样还是无凹槽试样，利用Ludwik模型计算得到的其在单轴拉伸条件下的极限应变值均接近NADDRG经验数据，但利用H-S模型计算得到的则远高于NADDRG经验数据，这归因于这两个模型中应变硬化指数的差异。上述比较说明Ludwik模型更适合于Q-P-T钢，因此选择Ludwik模型进一步利用Swift-Hill模型对不同凹槽深度比的试样进行单轴拉伸条件下（ε2＜0）极限应变值的计算，计算所用的参数值在表3中给出，计算结果如图7所示。可见，无凹槽试样和45°凹槽试样的理论预测值均接近NADDRG经验数据，但无凹槽试样的理论预测值高于NADDRG经验数据，即高估了Q-P-T钢的成形能力，在工程使用中是不安全的。此外，45°／5%凹槽试样的理论预测值稍低于NADDRG经验数据，这为其在工程中使用提供了某种程度的安全性。但是，一旦凹槽深度比超过5%，理论计算值将会低估实际的成形极限应变值，而且与FLD测定的要求不符。

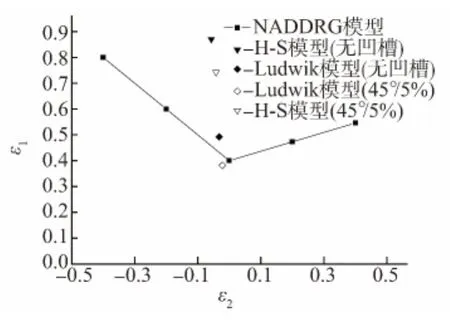
图6 单轴拉伸下Ludmik模型和H-S模型计算得到的极限应变值与NADDRG经验数据的比较Fig.6 Comparison between strain limit values calculated by Ludmik model and H-S model under uniaxial tension and NADDRG empirical data

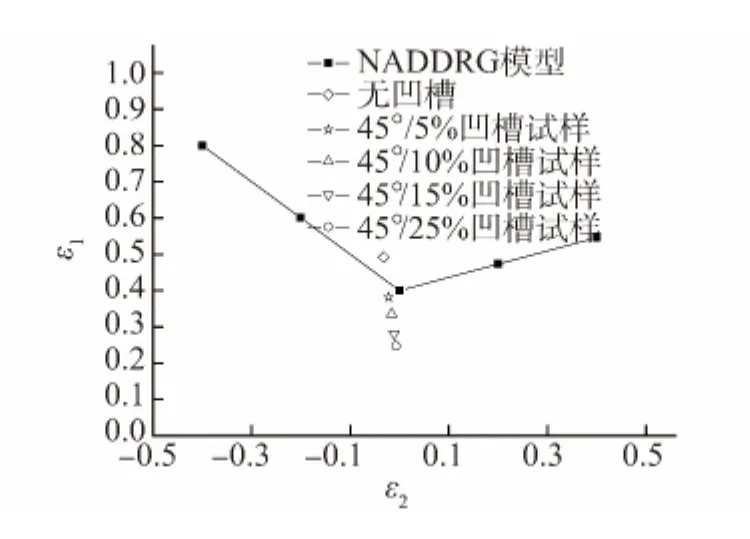
图7 应用Ludwik本构方程计算出的不同凹槽深度比试样的极限应变值与NADDRG经验数据的比较Fig.7 Strain limit values calculated by Ludwik model for samples with different groove depth ratios under uniaxial tension comparing with NADDRG empirical data

总之，材料不可避免地存在缺陷，成形试样厚度总会有微小的波动，因此引入凹槽缺陷对FLD进行理论预测是合理的。5%凹槽深度比可以满足成形性条件，凹槽深度比远大于5%的理论计算值将低估材料的实际成形能力，并且不符合FLD测定的要求。在凹槽深度比约为5%时，大于45°凹槽角的理论计算值也将低估材料的实际成形能力，而且随着凹槽角度增大，低估程度亦增加。因此，合适的FLD理论计算应取凹槽深度比为5%左右，凹槽角度等于或小于45°。上述单轴拉伸条件下极限应变的计算方法也适用于其它加载方式下极限应变的理论预测，例如采用式（5）可以计算出等双轴拉伸下的极限应变，该方法为构成完整FLD的计算奠定了基础。

3 结 论

（1）对于凹槽深度比一定的Q-P-T钢试样，随着凹槽角度减小，试样的塑性和强度均增大；对于凹槽角度一定的Q-P-T钢试样，随凹槽深度比增加，试样的塑性和强度均降低。

（2）与H-S模型相比，Ludwik模型更适合用于研究Q-P-T钢。

（3）利用Swift-Hill模型对单轴拉伸条件下的极限应变值进行计算，并与经验数据比较，确定出合适的FLD理论计算应取凹槽深度比为5%左右，凹槽角度等于或小于45°。

（4）单轴拉伸条件下极限应变的计算方法也适用于其它加载方式下极限应变的计算，该方法为构成完整FLD的计算奠定了基础。

［1］徐祖耀.用于超高强度钢的淬火-碳分配-回火 （沉淀）（QPT）工艺 ［J］.热处理，2008，23（2）：1-5.

［2］RONG Y H.High strength ductility steels treated by novel quenching-partitioning-tempering process［J］.International Heat Treatment ＆ Surface Engineering，2011，5（4）：145-154.

［3］ZHANG K，ZHANG M，GUO Z，et al.A new effect of retained austenite on ductility enhancement in high-strength quenching-partitioning-tempering martensitic steel［J］.Materials Science and Engineering：A，2011，528（29）：8486-8491.

［4］ZHOU S，ZHANG K，WANG Y，et al.The mechanism of high strength-ductility steel produced by a novel quenchingpartitioning-tempering process and the mechanical stability of retained austenite at elevated temperatures［J］.Metallurgical and Materials Transactions：A，2012，43（3）：1026-1034.

［5］SWIFT H W.Plastic instability under plane stress［J］.Journal of the Mechanics and Physics of Solids，1952，1（1）：1-18.

［6］HILL R.On discontinuous plastic states，with special reference to localized necking in thin sheets［J］.Journal of the Mechanics and Physics of Solids，1952，1（1）：19-30.

［7］MARCINIAK Z， KUCZYÑSKI K.Limit strains in the processes of stretch-forming sheet metal［J］.International Journal of Mechanical Sciences，1967，9（9）：609-620.

［8］ZHOU Y，NEALE K W.Predictions of forming limit diagrams using a rate-sensitive crystal plasticity model［J］.International Journal of Mechanical Sciences，1995，37（1）：1-20.

［9］ASARO R J，NEEDLEMAN A.Overview no.42texture development and strain hardening in rate dependent polycrystals［J］.Acta Metallurgica，1985，33（6）：923-953.

［10］WU P D，NEALE K W，VAN DER GIESSEN E.On crystal plasticity FLD analysis［J］.Mathematical，Physical and Engineering Sciences，1997，453：1831-1848.

［11］GB／T 228-2002金属材料室温拉伸试验方法［S］.

［12］KOC P，ŠTOK B.Computer-aided identification of the yield curve of a sheet metal after onset of necking［J］.Computational Materials Science，2004，31（1）：155-168.

［13］DZIALLACH S，BLECK W，BLUMBACH M，et al.Sheet metal testing and flow curve determination under multiaxial conditions［J］.Advanced Engineering Materials，2007，9（11）：987-994.

［14］余海燕，陈关龙，李淑慧.TRIP高强度钢板成形极限的实验研究［J］.中国机械工程，2001，15（23）：2158-2161.