考虑性能约束的卫星设备布局优化策略
2015-12-11张鹏,杨军
张 鹏,杨 军
(中国空间技术研究院,北京 100094)
考虑性能约束的卫星设备布局优化策略
张鹏,杨军
(中国空间技术研究院,北京 100094)
摘要:针对桁架式卫星舱内的设备布局需求,提出了一种新的考虑性能约束的卫星设备布局优化策略。首先,以桁架式卫星舱内设备布局设计为背景,建立了卫星设备布局优化的数学模型;然后,引入整数优化的思想,以待布设备的安装序列为设计变量,并提出逐次布局策略与局部调整策略,按照先左后右-先下后上的布局准则,由已知待布设备的安装序列求解获得各待布设备的安装位置,进而可得出待布设备的总质心位置;由于在逐次布局与局部调整阶段,即每次计算目标函数值过程中,已将散热能力约束与设备干涉约束考虑在内,故卫星设备布局优化问题可转化为无约束优化问题,降低了卫星设备布局优化的难度。最后,将该布局优化策略用于某卫星设备布局实例中,从优化结果上验证了卫星设备布局优化策略的正确性,该策略有效地降低了卫星舱内设备布局的设计难度,为提高桁架式卫星总体设计的效率提供了支持。
关键词:桁架式卫星;整数优化;布局优化;性能约束
随着国民经济和国防建设的快速发展,对大型通信卫星的需求日益增加,经过多年发展,我国通信卫星平台的设计已实现模块化、系列化和通用化,正朝超大型化平台发展。目前国际上主流通信卫星平台主要包括承力筒式、箱板式、桁架式三种构型,其中桁架式卫星平台具有结构简单、承载能力大、设计灵活等优势,成为当前超大型卫星平台设计的热点(如波音公司研发的BSS-702卫星平台)。卫星舱内设备布局既要满足几何空间的约束,同时还要保证舱板面积满足对应位置设备的散热需求,在此前提下还要尽可能降低卫星质心纵向高度和减少横向偏移,是一个非常复杂的优化问题,因此得到越来越多学者的关注[1-3]。
卫星设备布局优化问题是典型的三维布局问题,国内外学者均在该领域展开广泛研究[4-6]。国内学者中,腾弘飞[8-9]等针对卫星设备舱布局优化问题开展较多研究工作,分别采用启发式方法、数学规划法及灵敏度分析等方法进行卫星设备布局优化。冯恩民[10]引入图论思想,建立卫星舱内长方体群布局的优化模型,并研究适用于布局优化的全局优化算法。传统布局优化方法中的设计变量为待布设备安装位置的三维坐标,该类方法需进行大量计算以确定待布设备间的干涉情况,当待布设备数量较多时,设计变量的维度会大幅增高,导致优化效率急剧下降。
针对传统布局优化方法中设计变量维度较高从而导致计算效率低的问题,为满足桁架式卫星平台的实际工程应用需求,本文以待布设备的安装序列为设计变量,并提出逐次布局策略与局部调整策略,进而发展出基于整数优化的卫星设备布局优化策略。该方法的创新性在于引入整数优化思想,降低了布局优化问题设计变量的维度,同时,在逐次布局与局部调整阶段兼顾考虑散热能力约束与几何干涉约束,将原优化问题转为无约束优化问题,降低了优化设计的难度。
1 卫星设备布局优化模型
桁架式卫星平台相对现有的承力筒式在构型布局上存在较大差异,因此开展布局优化设计工作对提高其性能指标具有非常重要的意义,本文以桁架式卫星平台总体设计的实际需求为背景,建立卫星设备布局优化模型。如图 1所示,桁架式卫星平台舱体中四个贮箱并联放置,为提高空间利用率,同时保证平台模块化的总体设计思想,将设备安装在南北侧板一定区域内。

图1 简化桁架式卫星平台示意图
本文相关参考坐标系定义如下。
1)O:坐标系原点在卫星对接面几何中心上;
2)z:卫星平台的中心轴,由底面(对接面)指向顶面为正;
3)x:沿东西方向,其正方向为从原点指向卫星东板;
4)y:沿南北方向,其正方向为从原点指向卫星南板。
该参考坐标系用于计算卫星平台的质心坐标以及确定各待布设备的布局安装位置。对卫星设备布局要求可描述如下:
1) 包含所有待布设备的全舱实际质心位置与期望位置的误差,应尽量小;
2) 待布设备均安装在南北侧板上,且各安装板上所安装设备的热耗之和不超出该板的散热能力;
3) 各待布设备之间不得发生干涉,即互不重叠;待布设备的任何部分不得超出给定的布局空间,即不得与舱体发生干涉。
卫星舱内设备布局优化模型如下所示:
minf(x)=ε1g1(x)+ε2g2(x)+ε3g3(x)

(1)
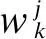
g1(x)=|xc-xe|
g2(x)=|yc-ye|
g3(x)=|zc-ze|
(2)
式中,xe、ye、ze为全部待布设备的期望质心,由设计者指定;xc、yc、zc为其实际的质心,其公式如下:
(3)
式中:n为待布设备的数量;mi为第i个仪器的质量;xi、yi、zi表示待布设备的质心在参考坐标系Oxyz中的坐标。假设待布设备均为立方体,且其质心位于其形心位置。
2 卫星设备布局优化策略
2.1 卫星设备布局优化策略
本文所提出的卫星设备布局优化策略主要包括两部分:
1) 将待布设备的安装序列作为设计变量,采用整数优化方法进行优化。而传统的整数优化方法无法直接对安装序列进行优化,故需要进行编码解码。
2) 根据给定的安装序列,按照本文所提出的逐次布局策略与局部调整策略,确定待布设备的安装位置,并计算其质心位置。
本文所提出的卫星设备布局优化策略流程图如图 2所示。

图2 卫星设备布局优化流程图
卫星设备布局优化策略的具体步骤如下:
(1)确定初始参数,包括待布设备的尺寸、热耗和质量信息,卫星舱体尺寸,散热能力。将待布设备依次编号为1,2,…,n,采用遗传算法进行优化,设计变量X为n维整数的向量,该优化问题的维度等于待布设备的数量,其上下限如下式所示:
(4)
(2)将设计变量X进行解码,将其表示为待布设备的安装序列X*(即不重复的1至n的整数序列)。设R为1至n顺序排列的整数序列,则解码后所得的安装序列X*可由式(5)确定:
(5)
首先将R中的第X(i)个元素赋予X*(i),然后将R中的第X(i)个元素赋空,即R中的元素个数变为n-i个,令i=i+1,逐次进行,直至i=n,则可获得待布设备的安装序列X*;
(3)获得待布设备的安装序列R*,按照逐次布局策略与局部调整策略(详见2.2~2.3节)对待布设备进行布局,获取其安装位置,并计算待布设备的质心位置;
(4)判断是否满足优化准则,若满足,则输出最优解,反之,继续优化。
2.2 逐次布局策略
逐次布局策略主要是根据已确定的待布设备的安装序列,在先左后右-先下后上准则下依次进行布局,其流程图如图 3所示。
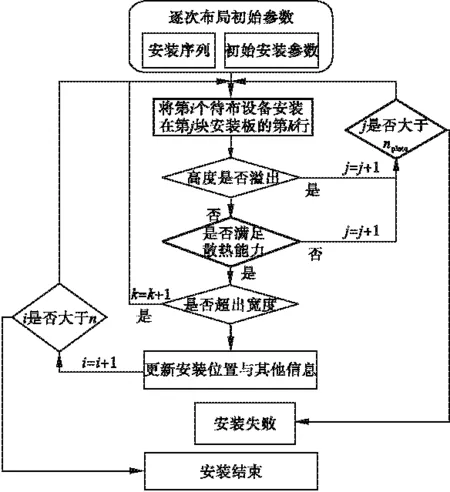
图3 卫星设备逐次布局流程图
先左后右-先下后上准则即首先将待布设备布置在安装板的左侧底部,后续的待布设备紧挨着已布置设备的右侧进行布置,若无法满足布局空间,则上升一层,以本层中已布置设备的最高边界作为更高一层的下边界,继续从左侧开始逐次布置剩余待布设备,如图 4所示。
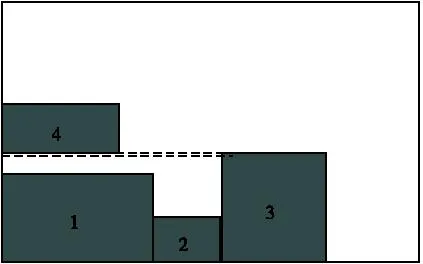
图4 先左后右-先下后上准则示意图
按照先左后右-先下后上准则,首先将待布设备1号从左侧底层开始安装,当进行4号待布设备的安装时,底层的剩余空间已无法满足4号待布设备的尺寸,故需将其布置在更高一层,由图 4可知,待布设备的安装位置偏向左侧,且4号设备可向下移动,故需要进行局部调整,以保证最终布局结果更加满足要求。
卫星设备逐次布局策略的具体步骤如下:
(1)确定初始参数,包括待布设备的尺寸、热耗和质量信息,卫星舱体尺寸,散热能力以及待布设备的安装序列,并i=1,j=1,k=1。
(2)将第i个待布设备布置在第j块安装板的第k行。判断待布设备i的高度是否超出安装板j的高度,若超出,则令j=j+1,转入第(3)步,反之则转入第(4)步。
(3)判断j是否大于nplate(表示安装板的数量),若j> nplate,则说明已无安装板可布置待布设备i,该安装序列下设备布局失败;反之,则转入第(2)步。
(4)判断待布设备i布置在安装板j后,安装板j上已布置的待布设备的总热耗是否超出该安装板的散热能力,若已超出,则令j=j+1,转入第3步,反之,则转入第(5)步。
(5)判断待布设备i布置在安装板j后,其边界是否超出安装板j的宽度,若超出,则令k=k+1,转入第2步,反之转入第(6)步。
(6)更新已确定的安装位置信息,安装板的剩余空间、剩余散热能力,并令i=i+1,转入第(7)步。
(7)判断i是否大于n,若i>n,则终止布局,输出各设备的安装位置信息,反之则令j=1,k=1,转入第(2)步。
通过逐次布局策略可实现待布设备的初步布局,仍需要进行局部调整,最终获得其安装位置。
2.3 局部调整策略
局部调整策略的主要目的是在初始布局后对待布设备的安装位置进行局部调整,以使目标函数更优,即待布设备的质心更接近期望质心位置。局部调整策略首先考虑进行水平方向移动,再考虑竖直方向移动,其流程图如图 5所示。
卫星设备局部调整策略的水平移动的目标是fxc=|xc-xe|越小越好,竖直移动的目标是zc越小越好。卫星设备局部调整策略的具体步骤如下:
(1)确定初始参数,包括待布设备的尺寸、质量信息和初始安装位置,卫星安装板尺寸以及期望质心位置,并i=n;
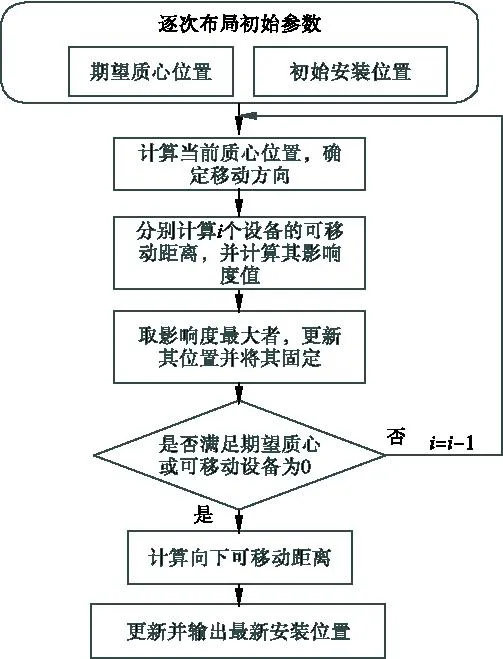
图5 卫星设备局部调整流程图
(2)计算当前全部待布设备的质心位置xc,与期望质心位置xe比较,若xc>xe,则沿x轴负方向移动,反之则沿x轴正方向移动;
(3)针对i个待移动设备,由是否超出安装板布局空间以及是否与其他设备干涉得出最大可移动距离,用步长试探法得出每个仪器的移动距离Δli,试探步长为5mm;
(4)计算各待移动设备的移动影响度值fiti=miΔli,选择fiti最大的设备i进行移动,更新其安装位置,并将其固定,不再进行水平移动;
(5)判断当前设备的质心是否满足期望要求,即fxc<δxe,其中δxe为可接受误差,若满足,则转入第6步,进行竖直方向移动,反之则判断待移动设备的数量是否为0,若不为0,则令i=i-1,转到第3步,反之则转入第(6)步;
(6)进行竖直方向移动,以使待布设备的质心高度最低。针对i个待移动设备,计算其可向下移动距离,计算各待移动设备的移动影响度值fiti=miΔli,选择fiti最大的设备i进行移动,然后将其固定,重复该步骤,直到待移动设备数量为0,转到第(7)步;
(7)输出待布设备的最新安装位置,至此,局部调整结束。
在已知待布设备的安装序列后,可通过逐次布局策略与局部调整策略获得待布设备的安装位置,进而可得出所有待布设备的总质心位置。
3 卫星设备布局优化实例
根据上述优化布局策略,利用Matlab软件编写了计算程序,同时以基于桁架平台的某卫星设备布局为例,进行了优化仿真工作,其中,进行整数优化所采用的优化算法为遗传算法,遗传算法的初始种群数量为100,最大迭代次数为100。该卫星舱体为六面体,尺寸为2500mm×2500mm×1800mm,待布设备均安装在南北侧板,其散热能力均为750W,南板编号为1,北板编号为2。使所有待布设备集合的质心沿Oz方向尽量低,且质心Ox轴和Oy轴坐标尽可能接近零,根据实际工程需求,可接受的误差设定为xc<10mm,yc<10mm。待布设备的质量、热耗及尺寸信息如表1所示。
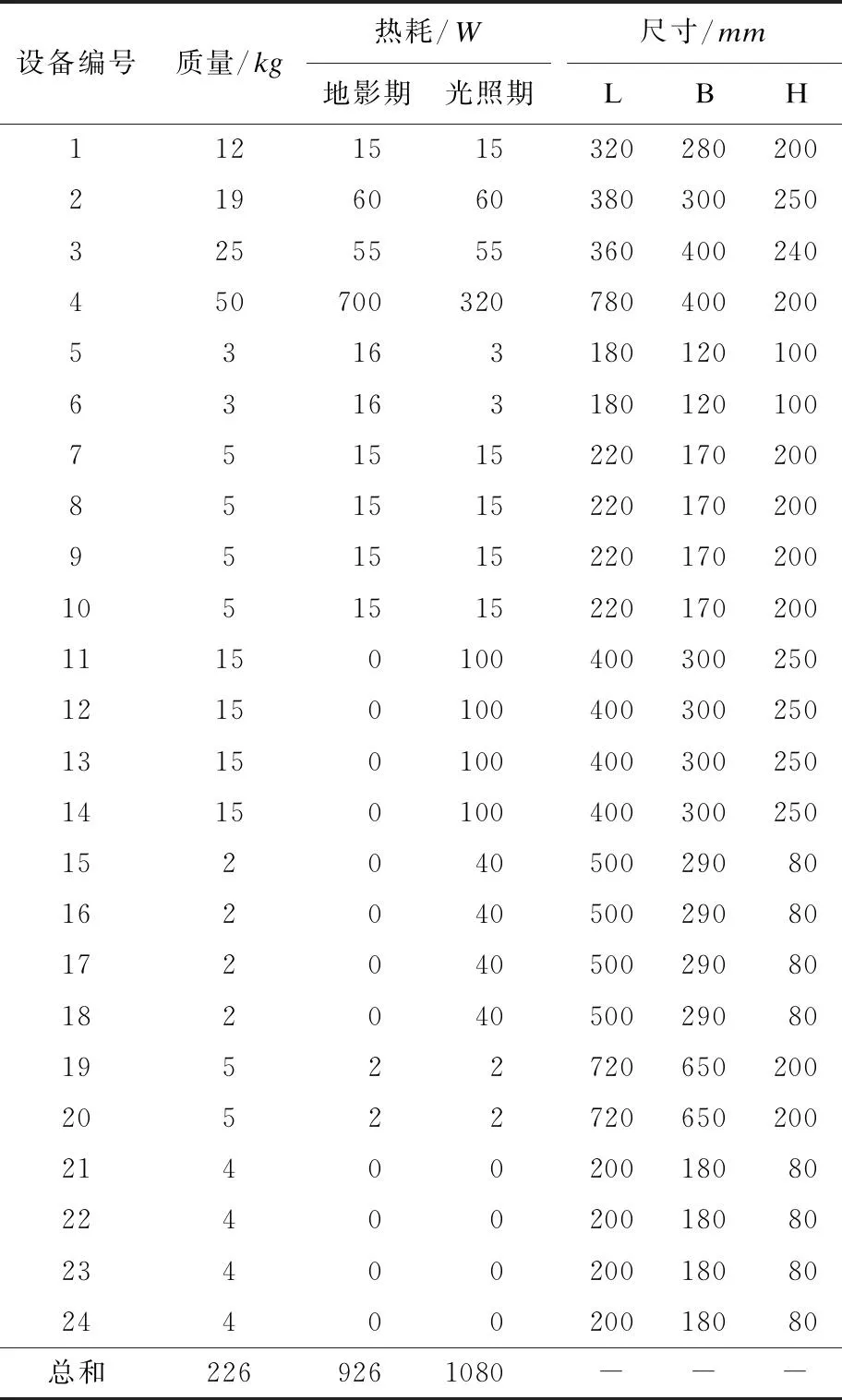
表1 待布设备信息
该实例中待布设备的数量为24,采用本文所提出的考虑性能约束的卫星设备布局优化策略(其设计变量的维度为24)与传统布局优化方法对该实例进行优化,传统布局优化方法即直接采用具有全局搜索能力的遗传算法,设计变量为待布设备的安装位置,其设计变量的维度为72。传统布局优化方法中遗传算法采用Matlab优化工具箱中的ga,初始种群为1000,最大迭代次数为100。其布局优化结果如表 2所示,其安装示意图如图 6至图 8所示。

表2 待布设备安装位置
由表 2可知,基于传统布局优化方法所得卫星设备的质心位置为xc=1.04mm,yc=11.05mm,zc=548.39mm;通过本文布局优化策略可得卫星设备的安装位置,卫星设备集合的质心位置为=xc-2.21,yc=-4.73,zc=199.87mm,其中,xc<10mm与yc<10mm,满足所设定的质心沿Ox轴和Oy轴方向的可接受误差。相比于基于传统布局优化方法所得卫星设备的安装位置,本文布局优化策略所得优化后的质心高度有较大改善。同时,本文布局优化策略所需时间也比传统布局优化方法少,需要指出,在仿真过程中,传统布局优化方法并不能保证每次都能找到满足约束的可行解。如图 7与图 8所示,由于本文所提出逐次布局策略采用先左后右-先下后上的准则,24个设备主要分为两层进行安装,淡蓝色表示上层设备,深蓝色为下层设备。
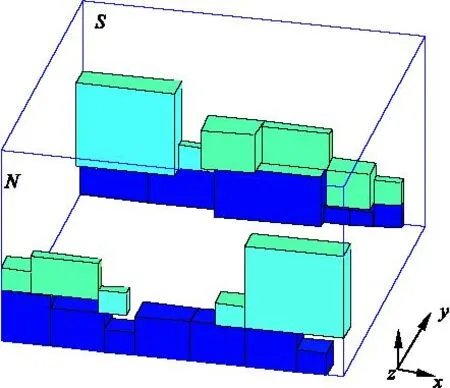
图6 卫星设备布局结果三维示意图

图7 卫星设备布局结果北板示意图

图8 卫星设备布局结果南板示意图
基于本文布局优化策略的优化过程中质心位置与目标函数值的变化如图9所示,虽然质心位置的变化曲线有上下波动,但目标函数值一直保持下降。在优化过程中,经过布局优化可获得设备安装信息,根据局部调整策略,设备的移动信息如表3所示,由于首先进行左右方向的移动(即第1次与第2次移动),第3次至第9次为向下移动,结合图7与图8可知,经过移动,可使设备的安装位置更优。
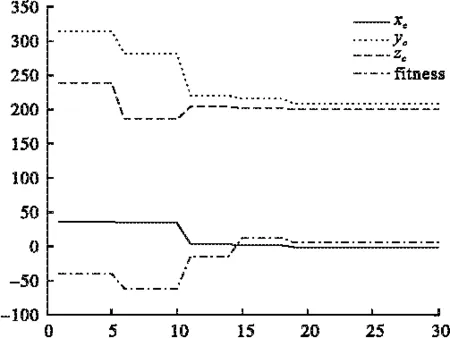
图9 优化过程中质心位置和目标函数值变化曲线图
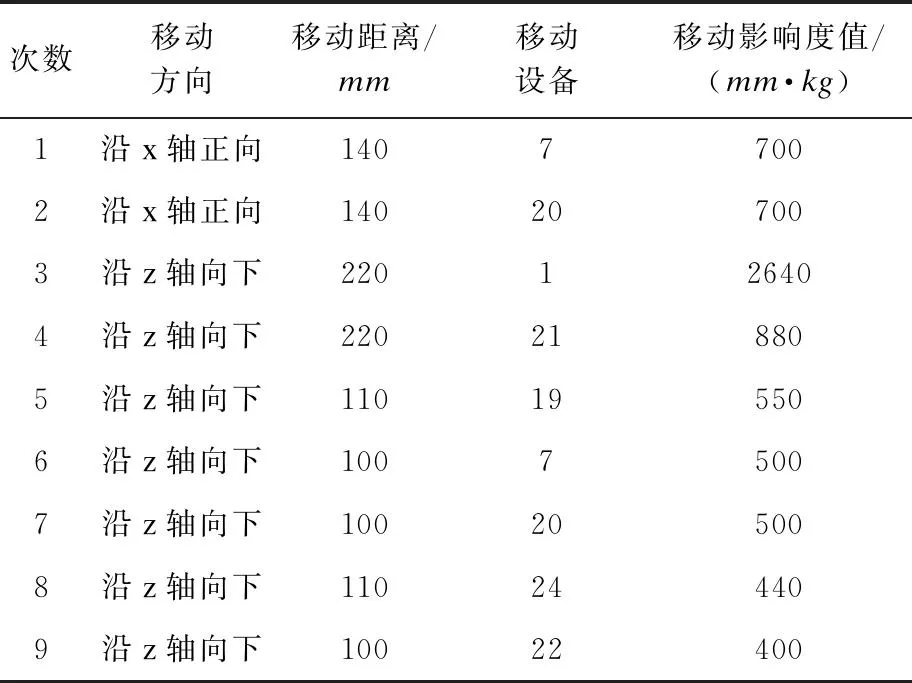
次数移动方向移动距离/mm移动设备移动影响度值/(mm·kg)1沿x轴正向14077002沿x轴正向140207003沿z轴向下220126404沿z轴向下220218805沿z轴向下110195506沿z轴向下10075007沿z轴向下100205008沿z轴向下110244409沿z轴向下10022400
4 结束语
桁架式卫星平台是一种全新的平台,开展设备布局优化工作意义重大。本文针对桁架式卫星平台的特点,建立了卫星设备布局优化模型,以待布设备的安装序列为设计变量,提出了兼顾散热能力约束与几何干涉约束的逐次布局策略与局部调整策略,以此来获得待布设备的安装位置,进而发展出了考虑性能约束的卫星设备布局优化策略,该方法相对于传统的以设备安装坐标为变量的方法可以极大提高计算效率。通过工程实例仿真表明:该优化策略有效地降低了卫星舱内设备布局的设计难度,提高了设计工作效率,可应用于卫星总体设计工作中。
参考文献:
[1]陈余军,周志成,曲广吉.多学科设计优化技术在卫星设计中的应用[J].航天器工程,2013,22(3):16-24.
[2]ZhiguoSun,HongfeiTeng.Optimallayoutdesignofasatellitemodule[J],EngineeringOptimization,2003,35(5):513-529.
[3]BaoZhang,HongfeiTeng,YanjunShi.Layoutoptimiz-ationofsatellitemoduleusingsoftcomputingtechniques[J].AppliedSoftComputing,2008,(8):507-521.
[4]TauraT,NagasakaI.Aadaptivegrowth-type3Drepresentationforconfigurationdesign[J].Arti.Intell.forEng.Des.Anal,1999,13(3):171-184.
[5]KamranD,MazarA,HossenSF.“Faragam”algorithminsatellitelayout[C].ProceedingsofthesixthAsia-PacificConferenceonMultilateralCooperationinSpaceTechnologyanApplications,Beijing,2001:120-127.
[6]VincentY.Blouin1,GeorgesM.Fadel,JoshuaD.Summers.Three-DimensionalPackingbyaHeuristic-basedSequentialGeneticAlgorithm[C].11thAIAA/ISSMOMultidisciplinaryAnalysisandOptimizationConference6-8Sep-tember2006,Portsmouth,Virginia.AIAA2006-6906.
[7]腾弘飞,孙守林,葛文海,等.旋转舱内圆柱体和长方体群布局优化[J].大连理工大学学报,1993,33(3):303-310.
[8]李言照,腾弘飞.旋转舱中长方体群的装填布局优化[J].宇航学报,1993,(1):37-43.
[9]邓四二,腾弘飞,邢玉生,等.一类带性能约束的二维几何布局优化[J].大连理工大学学报,1991,31(2):170-176.
[10]冯恩民,王锡禄.卫星舱内长方体群布局的优化模型及全局优化算法[J].运筹学学报,2001,5(3):71-77.
(责任编辑:马金发)
Layout Optimization Strategy of Satellite Module with Performance Constraints
ZHANG Peng,YANG Jun
(China Academy of Space Technology,Beijing 100094,China)
Abstract:According to the module layout design properties problem of truss satellite,a new layout optimization strategy of satellite module with performance constraints is proposed.Firstly,taking the module layout design of truss satellite as background,the mathematical model of satellite module layout optimization is constructed.Then the layout order of packing modules is regarded as the design variable with introducing the idea of integer optimization.The successive layout strategy and local adjusting strategy are presented and conformed to the layout principle of left-to-right and bottom-to-top.The spatial coordinates of all packing modules and the total mass center of all packing modules could be calculated by the known layout order of packing modules.As in the phase of successive layout and local adjusting,namely,the process of calculating the objective value,the heat dissipation capability constraint and module overlap constraint are taken into account,and then the satellite module layout optimization problem is transformed to non-constraints optimization problem and the difficulty of satellite module layout optimization is reduced.Finally,this layout optimization strategy is applied to an example of satellite module layout design and simulation results demonstrate the correctness of this layout optimization strategy.This strategy can effectively release the difficulty of satellite module layout design and provide much to improve the efficiency of truss satellite overall design.
Key words:truss satellite; integer optimization; layout optimization; performance constraint
中图分类号:V221
文献标志码:A
文章编号:1003-1251(2015)01-0022-07
作者简介:张鹏(1972—),男,高级工程师,研究方向:航天器总体设计.
收稿日期:2014-06-16
