GPS/INS紧组合导航姿态计算方法选取分析

黄运乾，程鹏飞，成英燕

(1.武汉大学测绘学院，湖北武汉430079;2.国家测绘工程中心，北京100039;3.国家测绘产品质量检验测试中心，北京100830;4.中国测绘科学研究院，北京100830)

一、引 言

GPS/INS紧组合导航是一种仅仅依靠GPS原始观测数据(伪距、伪距率)来和INS数据进行组合导航的一种模式。它的优点在于直接提取卫星接机中伪距、伪距率信息作为观测量，降低了量测噪声的相关性，并能在GPS可见卫星数小于4颗的情况下确保一定的导航精度;同时用补偿后的伪距、伪距率信息辅助接收机进行卫星捕获，有助于提高系统的导航精度、鲁棒性及抗干扰性能。

在惯性导航系统(INS)中，通过惯性测量单元陀螺和加速度计分别测得载体的角运动和线运动信息，导航计算机根据这些测量信息解算出载体的航向、姿态、速度和位置等导航参数。其中，姿态矩阵的解算相当于建立起数学平台，姿态矩阵一方面把加速度计的输出从载体坐标系变换到导航坐标系，然后进行导航计算;另一方面利用姿态矩阵的元素可以提取水平姿态角与航向角信息。姿态矩阵的计算，涉及载体姿态的实时解算，也关系到惯性导航平台的即时修正，姿态矩阵实时更新的速度和精度对导航系统的性能有着直接的影响，因此姿态更新算法性能的优劣直接影响捷联惯性导航系统的导航精度，是捷联惯性导航系统算法的核心。

姿态更新算法有方向余弦法、四元数法等，本文将方向余弦算法和四元数算法应用在GPS/INS紧组合仿真数据处理过程中，并对其结果进行比较，从而选择一种更适用于GPS/INS紧组合数据处理的姿态更新算法。

二、方法分析

1.方向余弦法

方向余弦矩阵(direction cosine matrix，DCM)用示，为3×3阶矩阵，矩阵的列表示载体坐标系中单位矢量在参考坐标系中的投影

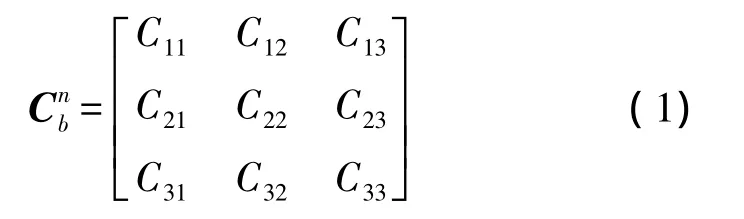
DCM表示矢量变换

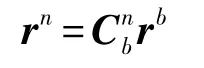
DCM随时间变化率

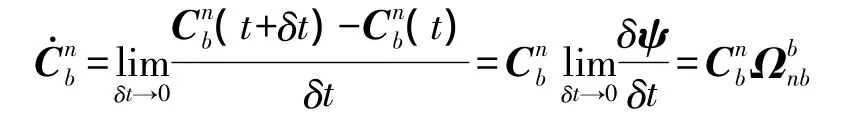
载体系b系相对导航系n系在载体轴系的转动角速度为

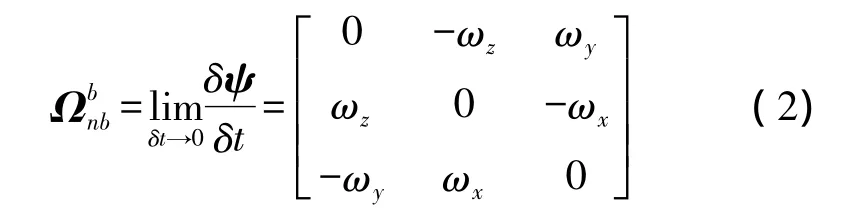
其分量形式为

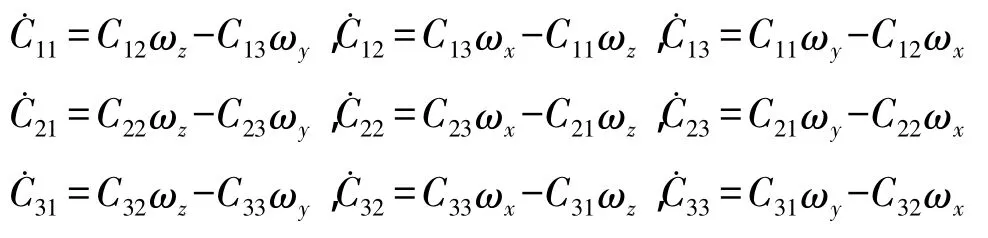
从上式可看出，方向余弦矩阵求解姿态矩阵时规避了欧拉方程退化的现象，未分方程是线性且非常简单的，可以全姿态工作，但同时要求解9个一阶微分方程，计算量大。

2.四元数法

四元数最早由Hamilton于1843年提出，四元数由1个实数和3个虚数组成，它是四维空间中的一个矢量，但其3个虚数又具有三维空间中的矢量性质。因此，任何三维空间中的一个矢量，都可以看作是一个实部为零的四元数，这个四元数是三维空间中的一个矢量在四维空间中的映象。

四元数是由4个元素构成的数

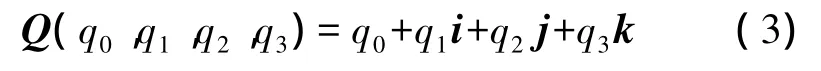
式中，q0、q1、q2、q3为实数;i、j、k 既是相互正交的单位向量，又是虚数单位。

并由它建立的微分方程组为

上述微分方程组中没有奇点，因此可以表述载体的所有姿态，同时其约束方程为

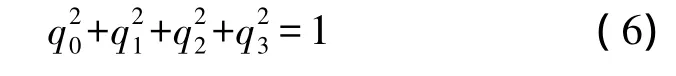
三、GPS/INS紧组合模式下的姿态方法选择

GPS/INS紧组合是一种依靠GPS原始观测数据(即伪距/伪距率)来进行组合导航的模式。它以INS相对GPS卫星的距离、速度与接收机测量获得的伪距、伪距率之差作为观测量，采用Kalman滤波等算法对惯导误差进行估计，并对惯导进行补偿。其算法流程如图1所示。

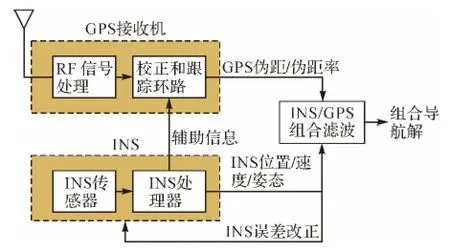
图1 GPS/INS紧组合模式

GPS/INS紧组合导航状态方程为

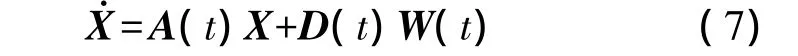
一般取15个状态变量，即

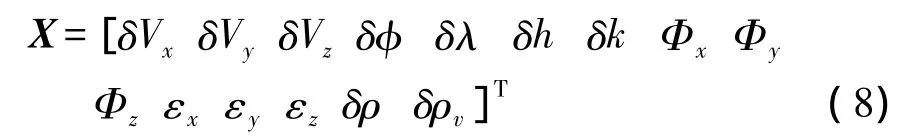
式中，δVx、δVy、δVz为惯导 3 个轴向的速度误差;δφ、δλ、δh分别为捷联惯导纬度、经度和高度误差;δk为游移角误差;Φx、Φy、Φz为平台姿态角误差;εx、εy、εz为陀螺漂移;δρ为接收机钟偏对应的伪距误差;δρv为接收机频漂对应的伪距率误差。

紧组合模式下，INS计算过程最主要的作用是通过计算姿态矩阵来给出载体的姿态和导航参数，以便将误差传递到滤波过程，并使GPS接收机向INS提供精确的位置和速度信息，辅助并帮助克服INS的长时间漂移误差积累;INS同时向GPS接收机提供实时的位置和速度信息，辅助GPS接收机内部的码/载波跟踪回路，提高GPS接收机的抗干扰能力和动态跟踪能力。

为了更好地对两种算法进行评估，应对姿态误差进行量化，并简约到几阶以内，可使结果保持在一个较好的精度水平。

1.方向余弦算法计算姿态矩阵误差

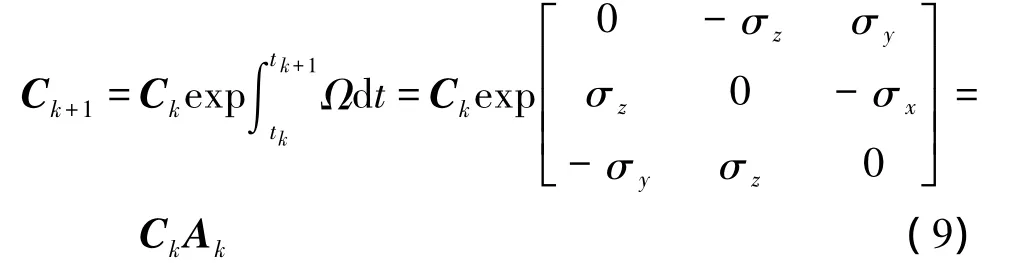
式中，Ck为第k次计算b系相对于n系的方向余弦矩阵;Ak为循环变换间的方向余弦矩阵;σ=为时间间隔内载体的旋转量，取

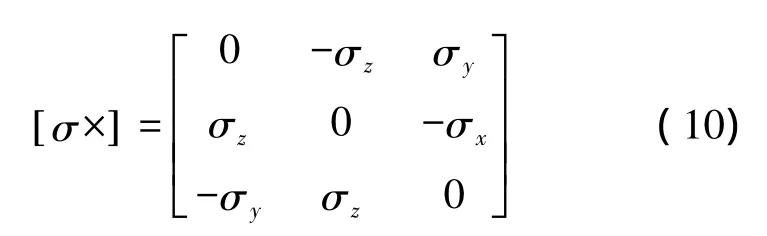
对式(10)进行指数项展开为

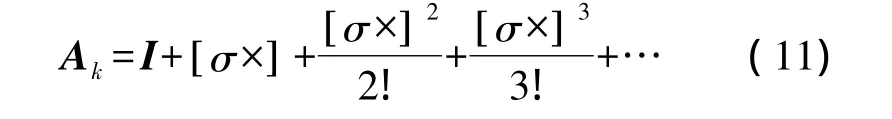
它的精度评估指标定义为Ddc，Ddc/δt可用来度量计算姿态矩阵的漂移。单一轴旋转情况下有

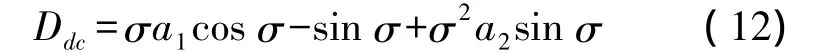
角增量(σ)最大值为0.1 rad 和0.05 rad 的情况下，假定载体最大角速度为10 rad/s，分别计算1、2、3、4阶下的漂移误差，可以得到姿态漂移误差在不同阶次使用方向余弦矩阵算法的大小变化，如图2所示。

图2 不同阶次下方向余弦算法计算的姿态漂移误差

2.四元数法计算姿态矩阵误差

当四元数表示的微分方程建立之后，可以通过在给定条件下用数值法来求解。设漂移误差参数为Dq，其表达式定义为

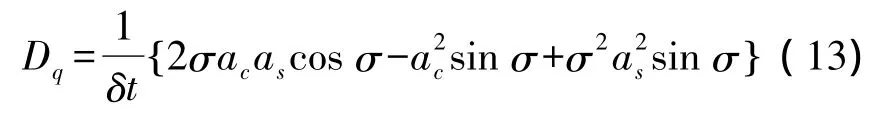
其中

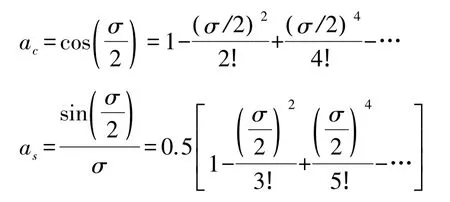
采用第1种算法在相同参数下，计算使用四元数算法的姿态漂移误差，可以得到姿态漂移误差在不同阶次四元数算法的大小变化，如图3所示。

四、结 论

1)通过以上对比分析可以得出，角增量最大值越小，计算的更新间隔越小，得到的精度也越高，这说明减小更新间隔可以得到更好的精度。在考虑轴旋转条件下，相同舍位阶数下四元数方法计算后得到的姿态漂移值要小于方向余弦法得到的结果。比如，同样计算三阶，最大角增量为0.1 rad的情况下，使用四元数算法得到的姿态漂移误差比方向余弦算法少 6.4°/h。

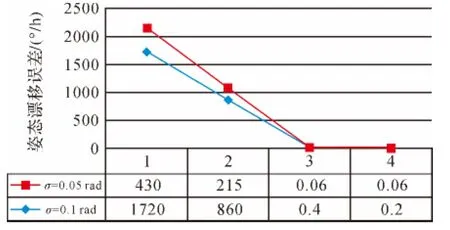
图3 不同阶次下四元数算法计算的姿态漂移误差

2)从算法解算方程可以看出，方向余弦算法需要解求9个参数，参数之间有6个约束方程，同时要解9个一阶微分方程，计算量大。而四元数所用参数为4个，参数之间有1个约束方程，而且四元数不论刚体处于任何状态都不会退化，所得到的方程组线性化程度高。因此，在GPS/INS组合导航过程中，四元数方法在适当环境下要优于方向余弦矩阵算法。

［1］周坤芳，李德武，周湘蓉.干扰环境下GPS/INS组合模式的研究［J］.中国惯性技术学报，2004，12(4):24-27.

［2］郭杭，刘经南.GPS/INS组合系统数据处理方法［J］.测绘通报，2002(2):21-23.

［3］陈哲.捷联惯导系统原理［M］.北京:宇航出版社，1986.

［4］秦永元.惯性导航原理［M］.北京:科学出版社，2006.

［5］李斐，束蝉方，陈武.遥感技术中GPS/INS组合系统的应用［J］.测绘通报，2004(12):1-4.

［6］郑辛，付梦印.SINS/GPS紧耦合组合导航［J］.中国惯性技术学报，2011，19(1):33-37.

［7］张晓亮.GPS/SINS组合导航系统应用研究［D］.南京:南京理工大学，2013.

［8］GREWAL M，WEIL L，ANDREWS P.Global Positioning Systems，Inertial Navigation and Integration［M］.New York:Wiley，2001.

［9］TITTERTON D H，WESTON J L.Strapdown Inertial Navigation Technology［M］.London:Institution of Electrical Engineers，1997.

［10］WANG C.Development of a Low-cost GPS-based Attitude Determination System［D］.Calgavy:University of Calgary，2003.

［11］ROGERS R M.Applied Mathematics in Integrated Navigation Systems［M］.2rd ed.［S.l.］:American Institute of Aeronautics and Astronautics Inc.，2003.