一种公共点坐标系转换中的粗差探测方法及其应用

杨福芹，戴华阳，邹定辉，杨国柱，马旺猛

(中国矿业大学(北京)地球科学与测绘工程学院，北京100083)

一、引 言

相似材料模型试验是矿山开采室内模拟研究的主要方法之一，其传统的观测方法通常是物理测量或机械测量，存在观测装置或传感器安装烦琐、工作量大、采样点有限等缺点［1-2］。近年来近景摄影测量技术用于相似材料模型试验观测模型测点的位移，克服了传统模型测量方法的缺点，具有测量数据准确、快速、信息容量大、可以实时动态监测模型测点的移动情况、自动化程度高的优点。杨化超等提出利用数字近景摄影测量技术量测模型变形，实现了实时或准实时的相似材料模型变形监测过程［3］。汤伏全等提出一种普通数码照相测定模型位移的方法，在测点周围布设独立的控制格网，通过获取控制格网角点和测点标志的图像坐标，从而解算各测点在独立控制格网中的实际坐标［4］。李欣等使用普通数码相机，采用多重交向摄影方式拍摄相似材料模型，得到变形点的坐标，并绘制累计位移矢量图［5］。这些文献都介绍了近景摄影测量用于相似材料模型试验的操作流程，但近景摄影测量坐标转换方面的研究不足。本文利用近景摄影测量用于相似材料模型试验，在对模型拍照过程中，由于外界因素(如人员走动、采动碰撞等)和内在因素(如全局点自身重力等)的影响，都会使控制点发生移动，导致基准的稳定性出现问题。因此，坐标转换过程中，若没有剔除这些存在粗差的控制点，将造成模型扭曲，出现错误的转换结果。为此，本文提出了近景摄影测量相似材料模型试验粗差探测算法。

二、坐标转换的六参数解算方法

如图1所示，设两个空间直角坐标系分别为OXYZ和Sxyz。根据坐标转换的物理过程，可得到

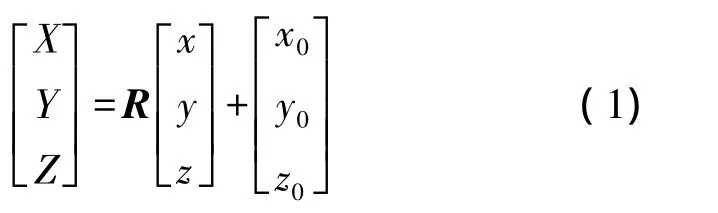
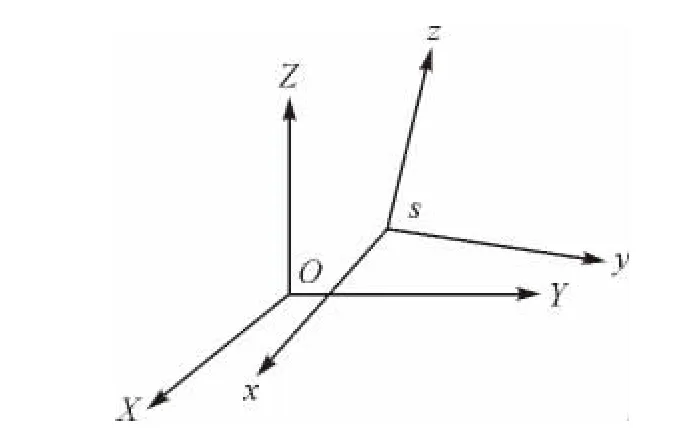
图1 两个不同的空间直角坐标

式中，R 为 3×3旋转矩阵;T=［x0y0z0］T为平移向量。此处假设两个坐标处理为同等长度基准，不考虑尺度因子。

解决摄影测量空间坐标变换，关键是确定旋转矩阵R和平移向量T。旋转矩阵R可由罗德里格矩阵3个独立参数a、b、c表示。引入反对称矩阵S

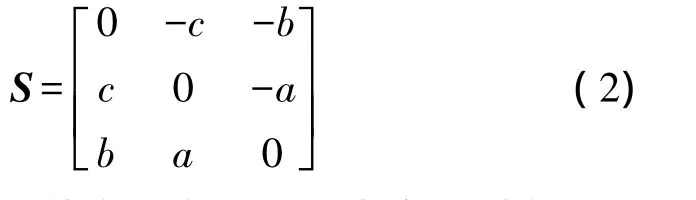
式中，a、b、c是3个独立的参数。R由实反对称矩阵S组成的旋转矩阵构成罗德里格矩阵。

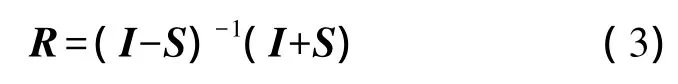
由式(1)可知，每一对公共点可列出3个方程，用第j对公共点的方程减去相应的第i对公共点的方程，可以消去平移参数T，得

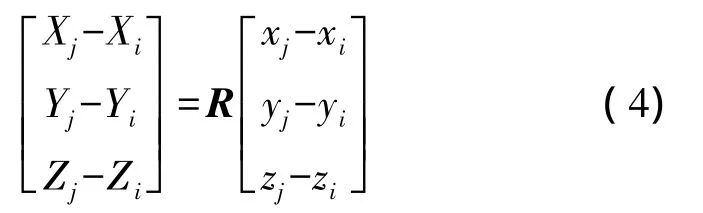
将式(3)代入式(4)可得

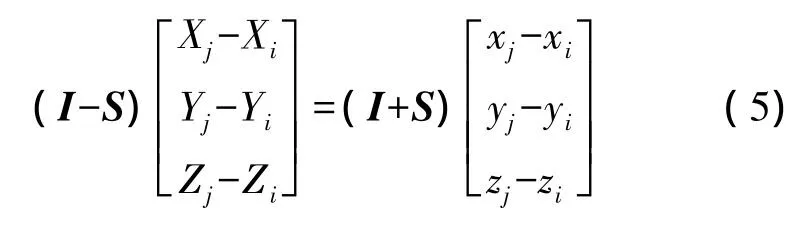
将式(2)代入式(5)，将方程组展开，把 a、b、c提取出来，写成向量的形式。整理可得

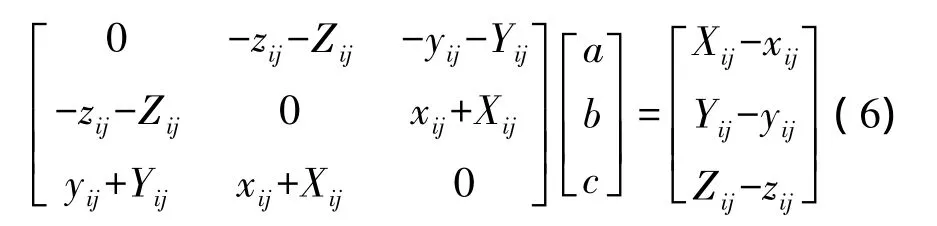
式中，Zij=Zj－Zi;Xij=Xj－Xi;Yij=Yj－Yi;xij=xj－xi;yij=yj－yi;zij=zj－zi。

式(6)左边系数矩阵显然为奇异阵，只有两个独立方程，用2组公共点无法直接求出a、b、c。同样，把点对k和点对i组成式(6)相同的方程。将两方程组联合，得

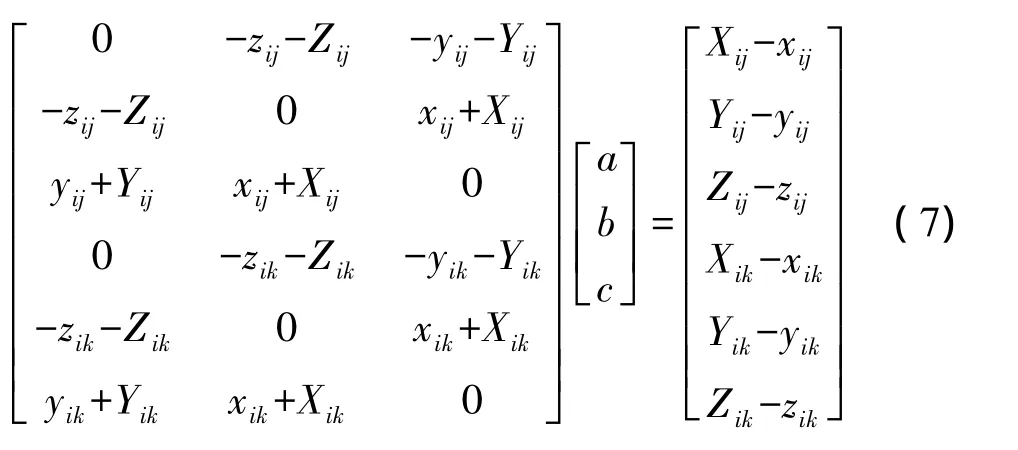
解式(7)方程即可求出 a、b、c 3个参数，根据式(2)、式(3)可求出旋转矩阵初值R，将控制点的一点对和旋转矩阵R代入式(1)可得平移参数初值T。

三、相似材料模型试验粗差探测算法研究

对于含有粗差的数据一般分为两种方法处理:一种是将含有粗差的观测值看作与正常观测值具有相同的方差、不同的期望;另一种是将含有粗差的观测值看作与正常观测值具有相同的期望、不同的方差［6］。本文根据第2种方法，采用三维光学摄影测量系统(digital close range industry photogrammetry，XJTUDP)进行静态变形工程，通过控制点进行不同状态的同名点坐标转换，由于在控制点转换过程中，会根据主观判断删除一些看起来配准误差比较大的点，存在着一定的随意性，而且在删除的过程中，控制点可能会集中在一侧，存在坐标转换误差大、精度严重降低等缺点，因此在进行坐标转换前需要对控制点进行粗差探测。相似材料模型是分析地表和岩层的下沉和水平移动趋势，在粗差探测的过程中，不考虑Z轴变化。

相似材料模型粗差探测算法如下:

1)对全局点进行排序，由坐标转换的六参数解算方法，求出旋转矩阵初值R和平移矩阵的初值T。按全局点顺序(A、B、C、D、E、F)三点组成一组向量，即，根据式(2)、式(3)、式(7)分别求解旋转矩阵R和平移参数T。

2)根据各组向量的旋转矩阵R和平移参数T，将变形状态下的全局点转换到基础状态下(假定基础状态下的坐标为真值)，与基础状态下坐标值作差，其配准误差分别为 ΔX、ΔY、ΔZ，即

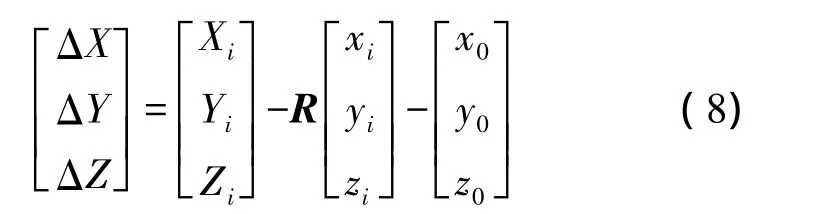
3)根据粗差理论［6］，比较方差大小，顺序排列，如果

说明控制点是可靠的，可以进行最小二乘坐标转换，δ是方差限差。

如果

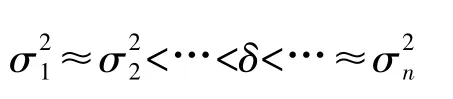
则说明有大于限差的方差，这组向量肯定含有粗差。

4)对含有粗差的向量进行组内判断。

根据最小二乘法原理，式(7)的误差方程为

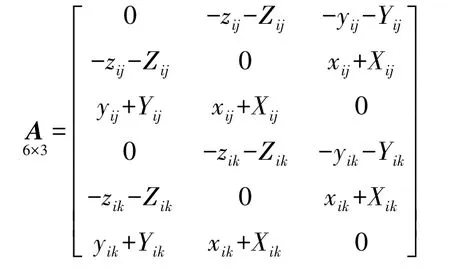
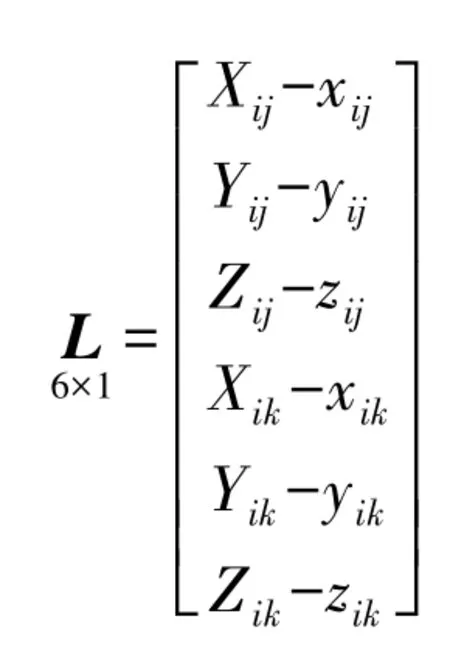
根据最小二乘原理，可得

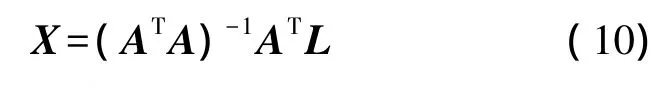
代入式(10)，可得

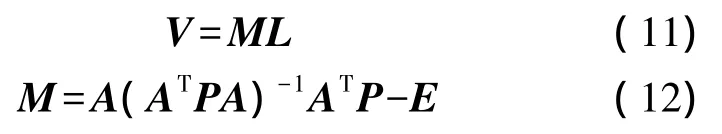
式中，M是可靠性矩阵;P是权阵，由于各点的坐标可以视作是同精度独立观测值，因此P=E，E是单位矩阵。

四、粗差探测算法应用研究

为了验证相似材料模型试验粗差探测算法及其应用的正确性，利用XJTUDP进行相似材料模型试验，如图2所示。本次试验采用数码相机尼康D90，主要参数为:相机分辨率4288像素×2848像素，传感器尺寸23.6 mm×15.8 mm，焦距24 mm。控制点和监测点都粘贴在模型架上，控制点坐标见表1。用XJTUDP进行控制点转换，转换后的方差为0.254 mm，而采用罗德里格矩阵三维坐标转换的方差为 0.099 76 mm。

图2 相似材料模型

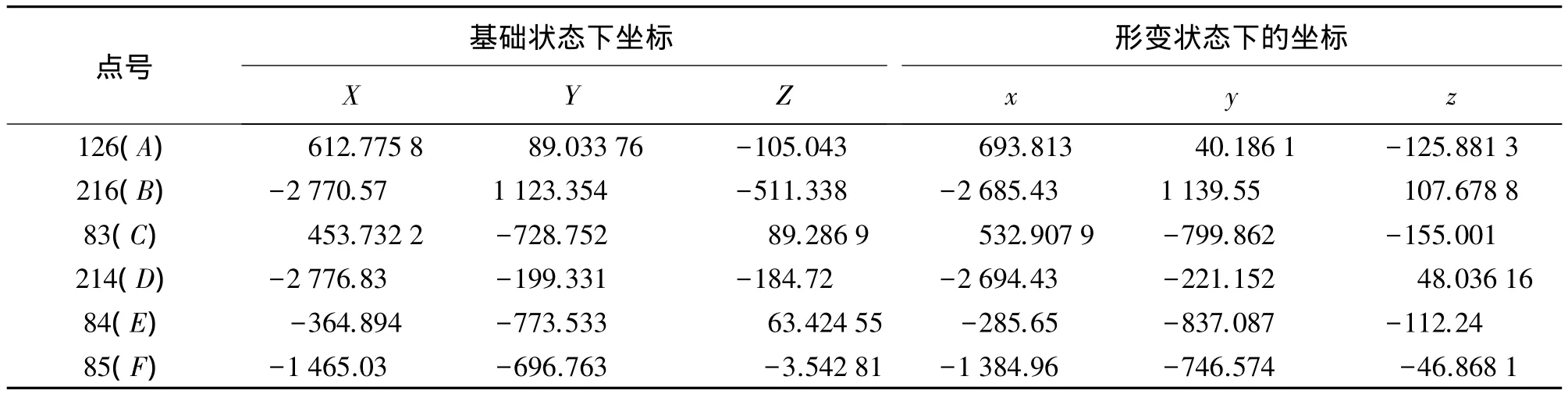
表1 不含粗差的公共点坐标 mm

在126(A)号点(x，y，z)坐标上加入5 mm的误差，加入粗差后的坐标见表2。采用罗德里格矩阵求初值的方法进行粗差探测。表3和表4是126(A)点未加入粗差和加入粗差后的方差。

表2 加入粗差后在形变状态下的坐标 mm

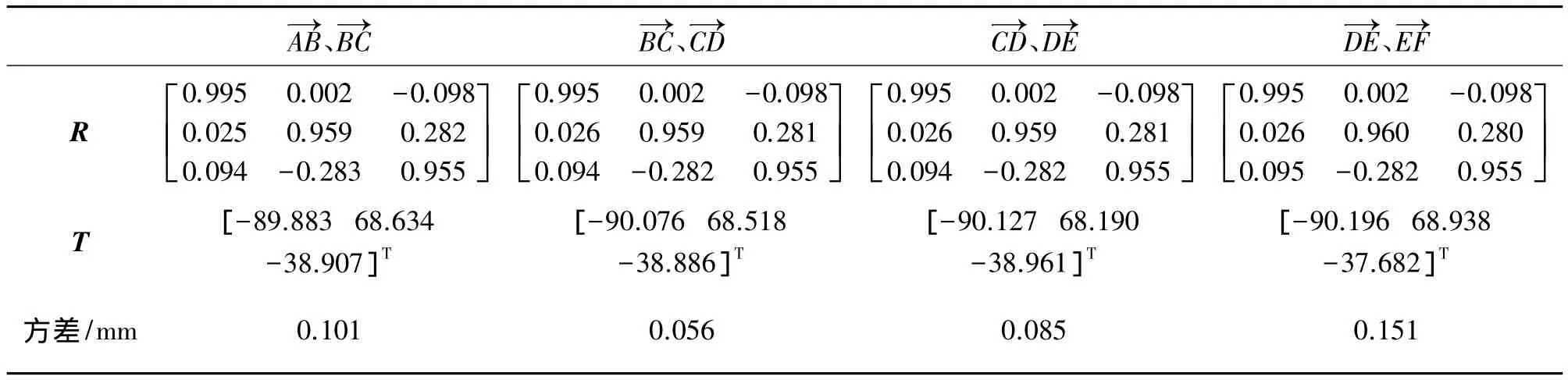
表3 A点未加入粗差的方差值

由表3可知，由各组初值求得的向量方差均在限差之内，认为这些点没有粗差，可以参与罗德里格矩阵最小二乘坐标转换。表4为126(A)点加入5 mm粗差后求得的方差向量，其值远远大于限差及其他方差，说明这组向量存在粗差，需要进一步定位粗差点。

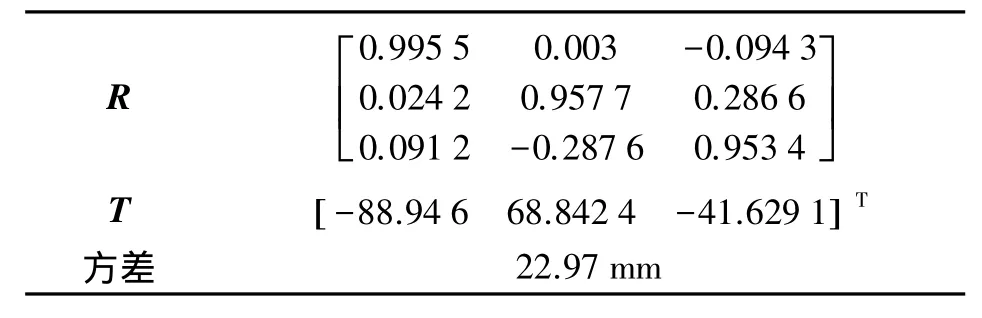
表4 126(A)点加入粗差的方差值

由式(11)得 x=［－0.147 0.047 5 0.005 4］T，把 x代入式(12)可得 V=［－3.904 3 －2.5 0.253 9 1.624 7 2.96 － 0.289 2］T，则11.401 3 mm，定位A点含有粗差。

剔除A点后，按罗德里格矩阵误差方程重新计算的坐标转换参数及方差见表5，此时计算的方差为0.074 3 mm，小于用 XJTUDP软件解算的方差0.248 mm。可见该方法不仅可以剔除粗差，还可以提高坐标转换的精度。

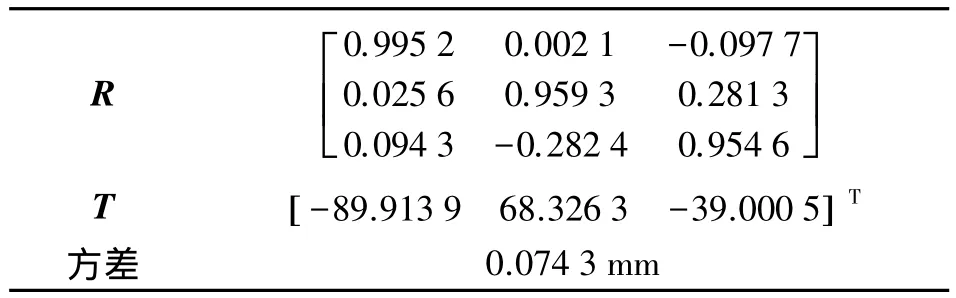
表5 剔除A点后的方差

五、结 论

1)本文针对相似模型试验近景摄影测量中精度要求高的问题，提出了基于罗德里格矩阵的坐标转换参数解算的模式和步骤，有效地解决了控制点数量少、分布不均匀等问题，取得了良好的应用效果。

2)通过近景摄影测量控制点向量组合和选择，提出了基于向量组合方差大小的粗差探测算法，提高了相似材料模型试验观测的可靠性。

3)粗差探测算法的计算量与控制点数量有关，模型试验观测时，可以通过选取分布较均匀的控制点来提高解算速度。

［1］何国清，杨伦，凌庚娣.矿山开采沉陷学［M］.徐州:中国矿业大学出版社，1991.

［2］陈兴华.脆性材料结构模型试验［M］.北京:水利水电出版社，1994.

［3］杨化超，张书毕，杨国东，等.基于非量测CCD相机和SVM的模型视觉检测［J］.吉林大学学报:工学报，2007，37(6):1375-1379.

［4］汤伏全，姚顽强，夏玉成.测定相似材料模型实验数据的数码照相方法［J］.辽宁工程技术大学学报:自然科学版，2008，27(3):333-336.

［5］李欣，陈从新，王兴玲.多重交向摄影用于矿山相似性材料物理模型变形测量［J］.武汉大学学报:信息科学版，2012，37(11):1294-1298.

［6］李德仁，袁修孝.误差处理与可靠性理论［M］.武汉:武汉大学出版社，2002.

［7］姚吉利，韩保民，杨元喜.罗德里格矩阵在三维坐标转换严密解算中的应用［J］.武汉大学学报:信息科学版，2006，12(31):1094-1096.

［8］周江文.经典误差理论与抗差估计［J］.测绘学报，1989，18(2):115-120.

［9］GUI Q，LI X，GONG Y.A Bayesian Unmasking Method for Locating Multiple Gross Errors Based on Posterior Probabilities of Classification Variables ［J］.Journal of Geodesy，2011，85(4):191-203.

［10］王建民，张锦，苏巧梅.观测数据中粗差定位与定值算法［J］.武汉大学学报:信息科学版，2013，38(10):1225-1228.

［11］周光文.地面摄影测量精度估算中的点位误差椭圆［J］.矿山测量，1997(1):34-36.

［12］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2007.

［13］陈西江，花向红，鲁铁定.基于组合罗德里格矩阵的异常特征点探测［J］.测绘科学，2011，38(4):94-96.

［14］吴祖海，罗伟钊，李军.坐标转换中公共点粗差定位与降低粗差点影响方法研究［J］.大地测量与地球动力学，2014，34(1):118-121.

［15］郭建锋，赵俊.粗差探测与识别统计检验量的比较分析［J］.测绘学报，2012，41(1):14-18.

［16］宋力杰，杨元喜.均值漂移模型粗差探测法与LEGE法的比较［J］.测绘学报，1999，28(4):297-329.

［17］张森林.罗德里格矩阵在共线方程严密解法中的应用［J］.武汉测绘科学大学学报，1987，12(1):81-91.