应用随机模拟试验进行概率统计研究性学习一例

杨玲香　姚斌

摘要：本文根据概率统计课程的特点，给出了在课程教学中应用随机模拟试验进行研究性学习的一个案例，既加深了学生对书本知识的理解，也锻炼了学生的应用能力。

关键词：模拟试验；概率统计；研究性学习

中图分类号：G642.41 文献标志码：A 文章编号：1674-9324（2015）07-0167-02

概率论与数理统计是大学生必修的公共数学课之一，它是研究随机现象统计规律性的一门学科，在现实生活中有着广泛的应用。与其他数学学科不同的是，概率论与数理统计基本概念和思想的深入理解占有极大的比重，解题方法和技巧并不多。而作为概率统计主要研究对象的随机现象又特别适合进行统计模拟。因此，笔者通过信息技术开展课程研究性学习，利用计算机及相应的编程软件对随机现象进行模拟，制作模拟试验，让学生亲自动手实践，可以将课程基础知识直观化，增加课程的趣味性，加深学生对基本概念的理解，取得良好的教学效果。

一、应用抛硬币试验讲解概率的频率定义

在讲解随机事件的概率这一节内容时，涉及到频率的稳定性讲解。课堂开始时，首先让学生回忆中学物理上有关频率的定义。同学们很快就异口同声地说出：单位时间内振动的次数。接着，告诉同学们数学上也有关于频率的定义，即在相同的条件下将试验重复进行n次，在n次试验中，事件A发生了fA次，fA称为事件在这n次试验中发生的频数，而比值Rn（A）=fA/n （1） 就称为事件A在这n次试验中发生的频率。

讲解了这个概念以后，可以让学生来观察一个简单的模拟试验——抛硬币试验。在模拟之前，先让学生想一想，如果抛一枚硬币多次，观察正反面出现的次数。那么，正面出现的概率应为多少？学生立马就能通过直觉及中学所学的简单概率知识就能答出：0.5。

接着，请某位同学运用抛硬币试验软件进行模拟，让学生从直观上感受不同试验次数时正面出现的频率。

再接着，我说历史上有很多著名的学者也都做过抛硬币试验。他们做的结果如表1。

显然，这些学者所做的结果也体现了我们所得出的结论。

有了这些试验结果做铺垫，我自然地引出频率稳定性的概念及概率的频率定义：当试验重复次数n很大时，频率会稳定在某一常数附近，我们称这个常数为频率的稳定值，就是我们所求的概率。

频率方法提供了概率的一个可供想象的具体值，并且在试验重复次数较大时，可用于给出频率的一个近似值。这个概念有两个关键部分，一个是试验的重复次数要足够大，另一个是要得出频率的稳定值。

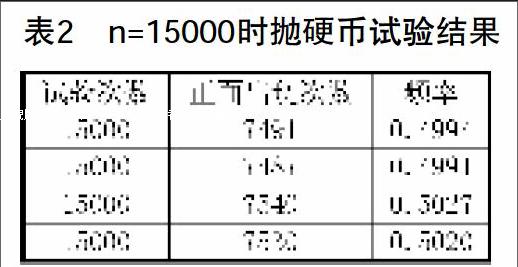
概念里的试验重复次数足够大，这是一个很模糊的字眼，到底多少次是试验次数足够大，15000次算不算足够大呢？如果设抛硬币试验的n=15000，统计正面出现的频率，让学生将这一试验重复4次，记录其结果如表2。

而把概率定义成频率的稳定值，也就是通过频率来估计概率，可即使在相同的条件下重复多次试验，得到的频率值都是不一样的，这是由随机性所决定的，但多次试验时频率具有一定的稳定性。

这个概念看似简单，但背后却隐藏着不少疑点，如果仅仅将概念在课堂上简单一讲便进入到后续内容，学生将会把这些问题遗忘，最终导致课程没学到位。但这些疑点在本次课程中也无法从根本上解决。因此，课程内容讲完后，我便给同学们留了一道家庭作业，就是希望同学们能够通过所学的VB程序设计语言，自己开发验证频率稳定性的抛硬币模拟试验，并在实践中思考概念的疑点。没想到，在第二次上课时，就有两组同学主动告诉我已完成了模拟试验。两组同学的抛硬币试验，虽然基本原理一样，但有一个学生设计的相对比较简单，主要是输入次数，然后显示正面出现的次数及频率。另一位同学的界面就相对丰富一些，既包含了上述这些内容，还包含了柱状图，饼状图等基于统计学的一些表示方法。

一个简单的模拟抛硬币试验在同学们的手中可以变得如此丰富多彩，也让我看到了学生们的求知欲和渴求创新的火花。但是，对于概念的疑点，同学们似乎都没有进行深层次的挖掘。

二、模拟试验引出大数定律，解释其理论依据

在讲到大数定理这一节的时候，我带领同学们重温了概率的频率定义，并请大家思考，这个概念的理论依据是什么？频率与概率到底有什么关系呢？同学们表现的很沉默。

1000，10000，m=50。为了节省时间，我让每组同学只做其中一种情况，最后由学习委员汇总大家的结果，后来，我请同学们观察表中的结果是否有什么规律？很快就有同学说，随着试验次数的增大，在多次试验中，正面出现的频率与概率非常接近。我马上接话：不错，这一现象用数学的语言来描述其实就是著名的伯努利大数定律。

三、中心极限定理给出估计误差

再次上课时，我便问同学们，上节课给大家布置的散点图是否具有规律性？有同学说散点图有点像正态分布的曲线。我接着说，同学们的理解是对的，下面我们就来介绍关于这一现象的棣莫佛—拉普拉斯中心极限定理：

这个关系式给出了用频率估计概率的误差。从这个误差计算公式中可以看出，试验次数n的大小决定着估计的误差大小，随着n的增大，误差会逐渐减小。可用于解决用频率估计概率的计算问题。所以在不同的实际问题中，试验次数n不是固定的，应根据问题对精度的要求来确定n的最小取值。至此，这一概念的疑点才算是彻底解决了。

以往在讲解大数定理和中心极限定理的内容时，我们虽然说这些内容是个概率统计的精华部分，但大多数学生都觉得这些只是些枯燥的定理。在讲解上，由于学时的压缩，只有2～4学时的时间。学生学过后都不知所以然，更不用说去解决课程前面遗留的问题。本文运用现代信息技术强大的计算功能，通过编制简单模拟试验开展研究性学习，把概率论的内容从教师的模拟、疑问，转变为学生自己实践验证，再到后来的讨论，引入新内容，前后联系，课内与课外相结合，既解决了前面内容的疑问，又加深了后续内容理论基础。也为学生学习统计学部分打下了坚实的基础。

参考文献：

[1]王金红.大学数学实施研究性学习的若干途径[J].大学数学，2007，23（4）.

[2]盛骤，谢式千.概率论与数理统计及其应用[M].北京：高等教育出版社，2004.

[3]张丽华，王颖喆.概率论教学的探索与实践[J].数学教育学报，2010，19（3）.

[4]张淑梅，张唯一.初中“用频率估计概率”的教学解析[J].数学通报，2010，49（1）.endprint