基于粒子系统的喷泉模拟实现
2015-12-10张刚靳继红
张刚 靳继红
摘要:喷泉模拟过程是一种非常复杂的对不规则模糊物体的模拟过程。文章采用基于粒子系统的图形生成算法,成功模拟了喷泉这种不规则模糊物体,经过实验,当粒子数目取得合适时,可以满足模拟精确性和实时性的要求。
关键词:喷泉模拟;粒子系统;三维建模; OpenGL
中图分类号:TP391 文献标识码:A 文章编号:1009-3044(2015)26-0210-02
1 引言
近年来,随着计算机技术的快速发展,对不规则模糊物体的运动模拟要求越来越多,也越来越精,尤其在影视广告、游戏开发、虚拟现实等领域,烟、火、云、水、、雨、雪等特效成为不可或缺的元素。几何外形表现不规则,且形态随时在动态地发生变化,这使得要生成这些对象不能用常规的三维建模方法[1]。粒子系统建模方法从1983年被Reeves[2]首次提出以来被认为是模拟不规则模糊物体最为成功的图形生成算法。本文拟采用粒子系统方法生成喷泉的三维模型对其进行模拟。
2 粒子系统
基于粒子系统方法的基本思想[3]是把大量基本粒子放在一块来描述这些不规则物体,基本粒子具有生命周期和属性,绘制出这些基本粒子,即可得到不规则模糊物体。基本粒子的属性不是单一的,包括大小,颜色、位置、速度、透明度和生命周期等一组属性。为模拟需要,赋予每个粒子一定的生命周期:出生、生长、衰老和消亡。所以粒子系统不是静态系统,而是各个基本粒子在时刻变形和运动。在变形运动中不断有新粒子生成并加入系统,旧粒子消亡退出系统。值得注意的是其中粒子每个属性的参数都是个随机数,可以很好地描述不规则模糊物体的随机性和动态性。
3 喷泉系统三维模型及模拟实现
3.1 喷泉模型
建立喷泉模型,首先要构造合适的空间坐标系。假设观察者的视点位于屏幕正前方,原点O在喷泉发射位置中心,三个坐标轴取向为: x轴正向取从左至右的方向,y轴正向取从下至上的方向,z轴正向为从里至外的方向,符合一般取向。
水珠,定义为:
[Rn={Pos,Speed,Size,Direction,Color,Bright,Age,Type}],实际上是一个n维向量,描述的是粒子的空间位置、速度矢量、方向、大小,颜色、亮度、年龄,生命周期、状态等属性。
水线是具有相同初始喷射方向的水珠粒子集合,记为[Fv]。
水线集:由一定数目的水线构成的集合[F],[F=q|q∈Fv] 。
喷泉基本模型:由一定数量水线构成的。假设不计空气阻力水珠在[y]方向只受重力作用,粒子在[y]方向运动轨迹则可描述为:
[y=-1/2*g*T2+H] (1)
其中g是重力加速度,[T]是生存时间,H表示水珠在[y]方向得最高值。
水珠在[x],[z]方向的位置分别由(2)(3)式确定。
[x=x0+vxdt] (2)
[z=z0+vzdt] (3)
其中[x0],[z0]是粒子在[x]和[z]方向的初始位置,[vx]和[vz]是粒子在[x]和[z]方向的速度。
喷泉模拟的实时性受水珠粒子数目的影响,过大过小均影响仿真效果。设屏幕上每单位区域平均出现粒子数为[PerArnum],方差为[Varnum], 水珠大小为[Size],显示区域为[Area],则初始时刻产生的粒子数目[Number]为:
[Number=(PerArnum+rand()×Varnum)×Area/Size]
其中[rand()]是随机函数,值可取在-1~+1之间。
3.2 喷泉系统模型实现
水珠粒子系统运动画面的生成绘制通常课按下面步骤进行[4]:
(1)新的水珠粒子生成,并加入粒子系统中;
(2)赋予每一个新水珠粒子一定的属性;
(3)刷新系统中水珠粒子属性;;
(4)删除已消亡的水珠粒子;
(5)检查粒子的动态属性,根据其变化情况对其进行移动和变换;
(6)将存活粒子绘制形成喷泉图形。
3.2.1 新水珠粒子的生成
模拟中,由坐标原点发射出水珠粒子,因此每个粒子的初始位置为O(0,0,0),粒子的其他各个属性要进行初始化[5](编程在Visual C++语言平台进行):
[v=(float)(rand()%a)/b+c] // 粒子运动初始速度
[d=(float)(rand()%e)/f+g] // 粒子运动初始方向
[xd=cos(π*d/180)*v/k] // 在X方向初始速度
[zd=sin(π*d/180)*v] // 在Z方向初始速度
[Type=True] // 运动状态,为真,则运动
[Alpha=1] // 粒子透明度
[H=100] // 粒子在空中位置高度的最大值
其中[a,b,c,d,e,f,g,k]为常量,其值由多次经验得到,[rand()]是随机数。
3.2.2 水珠粒子的位置更新
随着时间的推移,粒子不停地运动,其位置也在不断移动。设粒子在[tj]时刻经过[Δt]后到达[tj+1]时刻,粒子的位置发生的变化由公式(4)-(6)描述:
[xj+1=xj+vx*Δt] (4)
[yj+1=-1/2*g*t2j+1+H] (5)
[zj+1=zj+vz*Δt] (6)
粒子的高度值y随时间t变化,因为粒子喷出并落下的图形接近于开口向下的抛物线,因此y值先增加到最高然后开始减小。当[t=0]时,y取得最大值H。满足[y>0],则运动类型为真,即[Type=True],否则[Type=False],这个过程中,[Alpha]值淡化,直到为0,认为粒子消亡,删除即可。
3.2.3 粒子的消亡
从上面可以看出,粒子消亡决定因素有两个:运动类型[Type]和[Alpha]值。当粒子经历生成,上升到最高处,然后下落至水面后,运动类型Type值变为False。另外,变量[Alpha]表示粒子的透明度,再使用变量[ΔAlpha]来控制粒子到达水面后消融的速度[3]:
[Alpha=Alpha-ΔAlpha] (7)
粒子初始化时,其[Alpha]值为1,此时粒子完全不透明,能被完全看到,且显示颜色为本身的颜色。随着运动的不断进行,此值一直在减少,最终达到0值时,表明粒子消亡要从粒子系统中删掉。
3.2.4 粒子的绘制
我们要绘制的是所有在系统中活跃的喷泉粒子,当求出这些粒子的位置后开始绘制的工作了。实际中喷泉包含的粒子数量巨大,为简化绘制过程,本文采用了OpenGL标准图形库中提供的四边形为基本绘制单位,结合纹理映射功能及色彩融合技术生成各个水珠粒子。
绘制过程主要调用OpenGL函数。调用[glColor4f()]设置水珠粒子的颜色,调用设置当前纹理坐标,调用[glTexCoord2f()]设置纹理坐标,调用[glVertex3f()]进行纹理映射,调用[glEnable()]和[glDisable()]进行粒子融合。
4 实验结果
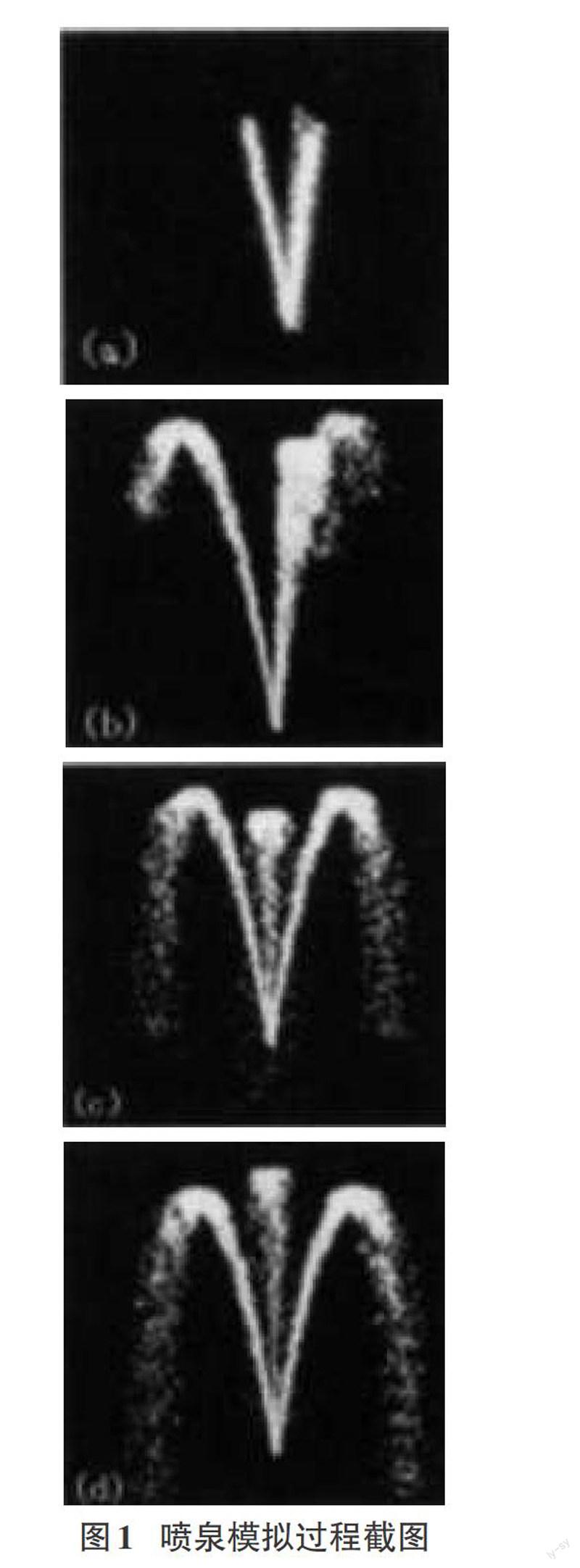
按照以上所述方法,喷泉的模拟主要使用OpenGL技术,运用VC++ 6.0语言为开发平台编程实现,效果如图1所示,(a)(b)(c)(d)所示为喷泉系统模型形成过程的截图。实验中,通过调整粒子数量来测试绘制速度,结果表明在粒子数量小于10000的情况下绘制速率较好,能满足实时性的要求。
5 结束语
本文使用OpenGL技术,以VC++6.0为开发平台实现了基于粒子系统的喷泉模拟过程,模拟效果真实自然,在将来更细致的研究工作中,还可以进一步考虑水珠落回水面后溅出水花效果。
参考文献:
[1] 任庆东,袁旭公,刘贤梅.基于GPU的喷泉模拟[J].科学技术与工程,2010,10 (36):9110-9114.
[2] Reeves W T,Lucasfilm.Particle Systems-A Technique for Modeling a Class of Fuzzy Objects[J].ACM Transactions on Graphics,1983,2 (2):213-217.
[3] 肖何,何明耘,白忠建.OpenGL中基于粒子系统的喷泉模拟实现[J].计算机仿真,2007,24(12):201-204.
[4] 蒋恒恒,汤宝平.基于OpenGL与粒子系统实现三维喷泉模拟[J].计算机测量与控制,2009,17(9):1717-1719.
[5] 汪继文,郑锋.基于OpenGL与粒子系统的喷泉模拟实现[J].计算机技术与发展,2011,21(8):161-164.
