差分进化算法在传热反问题求解中的应用

付剑波

摘 要：本文耦合差分进化算法和数值传热学求解方法，发展了一种新的传热学反问题求解方法。以二维对流换热反问题为例，高精度的反演了热流密度，证明了该算法的正确性和鲁棒性。考察了测量点数目对反问题求解的影响，计算表明存在一个最少测量点数，并给出了确定最少测量点数的方法。研究了测量误差对算法的影响。结果表明该算法具有很强的抗噪能力，证明该算法具有很强的稳定性和实用性。

关键词：差分进化算法；传热反问题；测量误差

引言：传热反问题在数学上常常是的不适定性， 其求解比正问题要复杂和困难得多。传热反问题具有以下特点：

（1）传热反问题的解具有不唯一性和不稳定性的特点；（2）目标函数与优化变量之间没有解析的函数关系式，目标函数的可微性难于保证，求解目标函数的梯度非常复杂；（3）目标函数具有多峰值、非凸函数的特点。本文采用新近发展并得到广泛应用的差分进化算法，耦合传热学数值求解方法，发展了一种新的反问题求解方法，并以高温超导实验中平行平板管道壁面热流密度的测量问题为例，验证了该方法的正确性和实用性。

一、差分进化算法简介

进化算法（Evolutionary algorithms）具有以下特点：1）寻优过程中仅利用函数本身的信息，对目标函数及约束条件的可微性、凸性没有要求，且对各类优化问题的处理流程基本一致，具有很强的通用性；2）具有较强的全局寻优能力和优秀的鲁棒性，能以较大概率收敛到全局最优解；3）采用随机优化算子而不是严格的确定性运算，可直接逼近多目标优化问题；4）采用群体搜索而不是单点搜索，对初始解没有要求。

由Storn和Price于1996年提出的差分进化算法（Differen

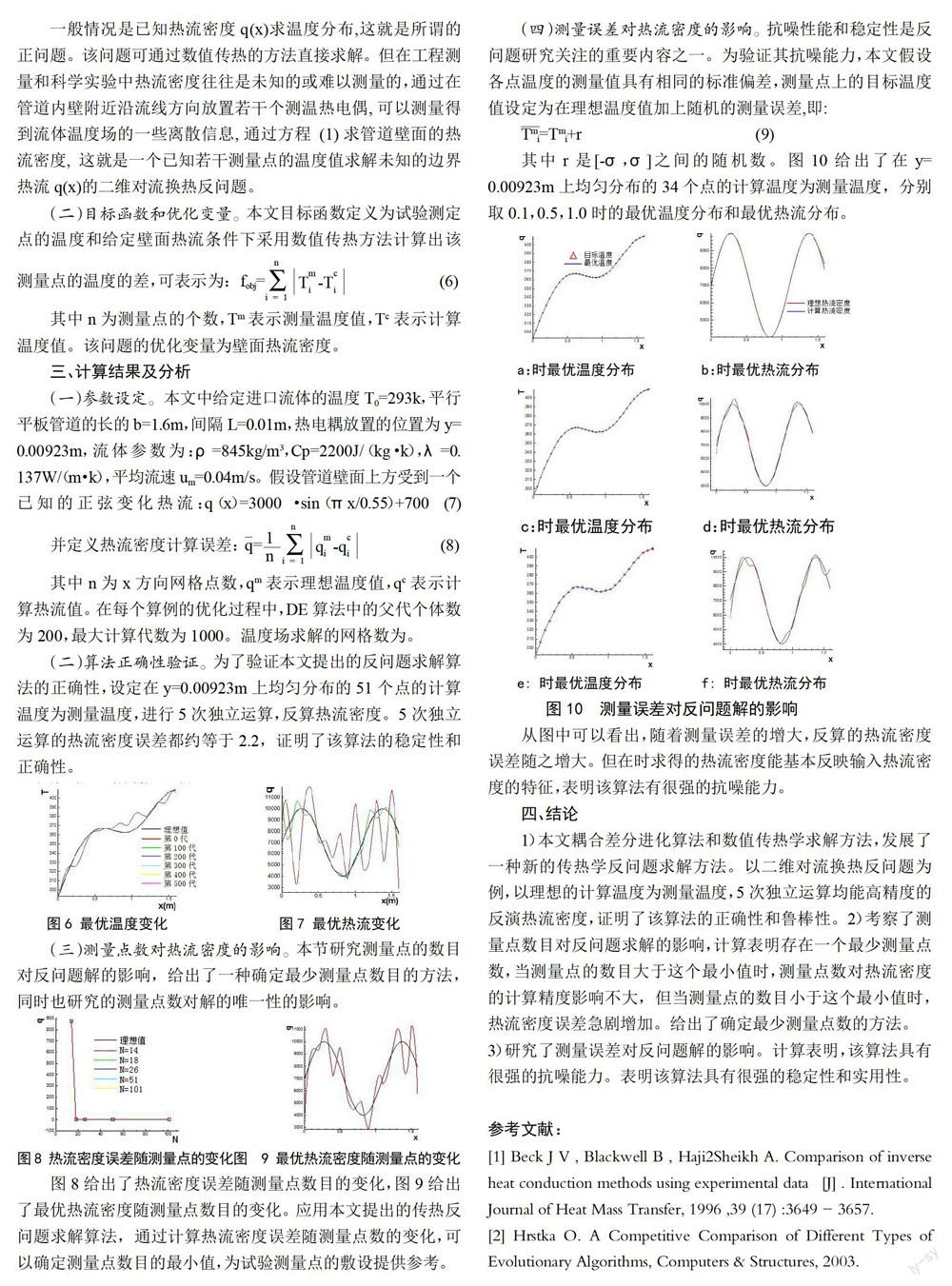
tial evolution，简称DE），是进化算法的一个重大改进，获得了广泛的关注。图1是DE算法的操作流程图。

DE算法通常采用实数编码，与传统的进化算法有两点区别：1）采用差分算子代替了传统进化算法中的交叉和变异算子；2）采用一对一选择策略生成新的种群。设第t代中第i个染色体表示为：CHti=（chti，1，chti，2，chti，j，chti，n） （1）

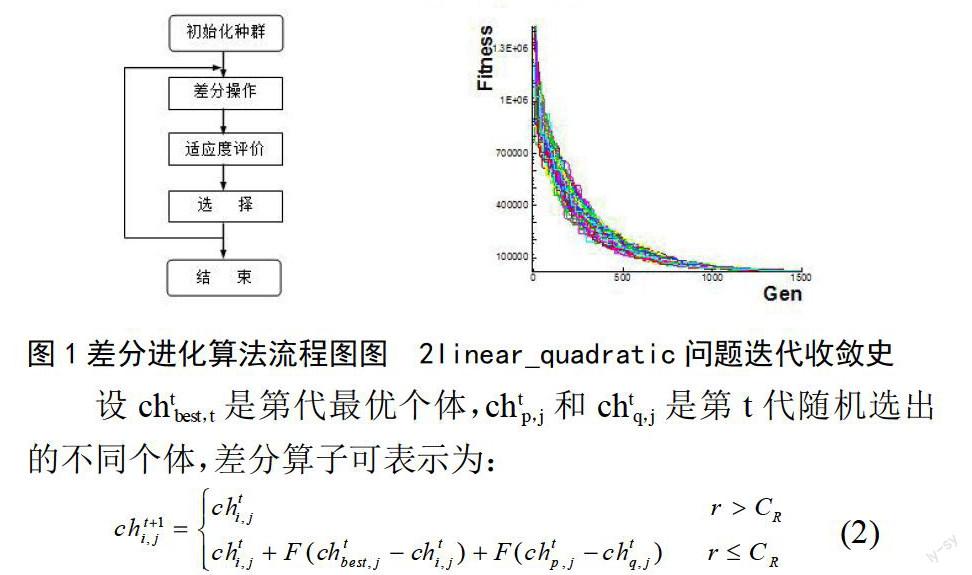
图1差分进化算法流程图图 2linear_quadratic问题迭代收敛史

设chtbest，t是第代最优个体，chtp，j和chtq，j是第t代随机选出的不同个体，差分算子可表示为：

（2）

其中r是[0，1.0]之间的随机数。DE算法操作十分简单，在寻优过程中只需要两个参数：定标因子F和阙值因子CR。其中F∈[0，1.0]，文中取0.85，CR∈[0，1.0]，文中取1.0。从式（2）可以看出，差分算子利用种群中多个个体的信息，正是这一特点使得

DE算法较传统的进化算法具有更优秀的鲁棒性和全局寻优能力。本文选择linear_quadratic问题，验证DE算法在处理多峰值、高维问题时的鲁棒性和全局寻优能力。linear_quadratic问题定义为：

（3）

其中ui∈[-200，200]， i﹦1，2，…，45。该函数具有参数相互关联的特点，优化难度相当大。对该函数，本文采用DE算法进行100次随机试验，图2给出了函数优化过程的迭代收敛史。

二、传热反问题求解方法及应用

本文以差分进化算法为核心，耦合数值传热学求解技术，发展了一种适用于求解传热反问题全局自动求解算法。图3是该算法的执行流程图。

图3 传热反问题求解算法流程图

（一）数学模型。本文考虑一个平行平板的层流受迫对流的情况。其中管道的一个壁面绝热， 而另一壁面受到随空间变化的热流。流体进入管道的流体温度为T0 ，如图4所示。

图4 二维对流换热问题示意图 图5 迭代收敛史

该问题的数学模型可表示为：

以um 表示流体的平均速度，u（y）可表示为：

一般情况是已知热流密度q（x）求温度分布，这就是所谓的正问题。该问题可通过数值传热的方法直接求解。但在工程测量和科学实验中热流密度往往是未知的或难以测量的，通过在管道内壁附近沿流线方向放置若干个测温热电偶， 可以测量得到流体温度场的一些离散信息， 通过方程（1） 求管道壁面的热流密度，这就是一个已知若干测量点的温度值求解未知的边界热流q（x）的二维对流换热反问题。

（二）目标函数和优化变量。本文目标函数定义为试验测定点的温度和给定壁面热流条件下采用数值传热方法计算出该测量点的温度的差，可表示为： fobj=■T■■-T■■ （6）

其中n为测量点的个数，Tm表示测量温度值，Tc表示计算温度值。该问题的優化变量为壁面热流密度。

三、计算结果及分析

（一）参数设定。本文中给定进口流体的温度T0=293k，平行平板管道的长的b=1.6m，间隔L=0.01m，热电耦放置的位置为y=

0.00923m，流体参数为：ρ=845kg/m3，Cp=2200J/（kg·k），λ=0.

137W/（m·k），平均流速um=0.04m/s。假设管道壁面上方受到一个已知的正弦变化热流：q（x）=3000 ·sin（πx/0.55）+700 （7）

并定义热流密度计算误差： q=■■q■■-q■■ （8）

其中n为x方向网格点数，qm表示理想温度值，qc表示计算热流值。在每个算例的优化过程中，DE算法中的父代个体数为200，最大计算代数为1000。温度场求解的网格数为。

（二）算法正确性验证。为了验证本文提出的反问题求解算法的正确性，设定在y=0.00923m上均匀分布的51个点的计算温度为测量温度，进行5次独立运算，反算热流密度。5次独立运算的热流密度误差都约等于2.2，证明了该算法的稳定性和正确性。

图6 最优温度变化 图7 最优热流变化

（三）测量点数对热流密度的影响。本节研究测量点的数目对反问题解的影响，给出了一种确定最少测量点数目的方法，同时也研究的测量点数对解的唯一性的影响。

图8 热流密度误差随测量点的变化图 9 最优热流密度随测量点的变化

图8给出了热流密度误差随测量点数目的变化，图9给出了最优热流密度随测量点数目的变化。應用本文提出的传热反问题求解算法，通过计算热流密度误差随测量点数的变化，可以确定测量点数目的最小值，为试验测量点的敷设提供参考。

（四）测量误差对热流密度的影响。抗噪性能和稳定性是反问题研究关注的重要内容之一。为验证其抗噪能力，本文假设各点温度的测量值具有相同的标准偏差，测量点上的目标温度值设定为在理想温度值加上随机的测量误差，即：

Tmi=Tmi+r （9）

其中r是[-σ，σ]之间的随机数。图10给出了在y=

0.00923m上均匀分布的34个点的计算温度为测量温度，分别取0.1，0.5，1.0时的最优温度分布和最优热流分布。

从图中可以看出，随着测量误差的增大，反算的热流密度误差随之增大。但在时求得的热流密度能基本反映输入热流密度的特征，表明该算法有很强的抗噪能力。

四、结论

1）本文耦合差分进化算法和数值传热学求解方法，发展了一种新的传热学反问题求解方法。以二维对流换热反问题为例，以理想的计算温度为测量温度，5次独立运算均能高精度的反演热流密度，证明了该算法的正确性和鲁棒性。2）考察了测量点数目对反问题求解的影响，计算表明存在一个最少测量点数，当测量点的数目大于这个最小值时，测量点数对热流密度的计算精度影响不大，但当测量点的数目小于这个最小值时，热流密度误差急剧增加。给出了确定最少测量点数的方法。

3）研究了测量误差对反问题解的影响。计算表明，该算法具有很强的抗噪能力。表明该算法具有很强的稳定性和实用性。

参考文献：

[1] Beck J V ， Blackwell B ， Haji2Sheikh A. Comparison of inverse heat conduction methods using experimental data [J] . International Journal of Heat Mass Transfer， 1996 ，39 （17） ：3649 - 3657.

[2] Hrstka O. A Competitive Comparison of Different Types of Evolutionary Algorithms， Computers & Structures， 2003.