具有有界干扰的耦合谐振子网络的一致性

范龙云，朱善华，徐承杰，文 平，文 伟

（1. 湖南工业大学 理学院， 湖南 株洲 412007；2. 湖南工业大学 冶金工程学院，湖南 株洲 412007）

具有有界干扰的耦合谐振子网络的一致性

范龙云1，朱善华1，徐承杰1，文 平2，文 伟1

（1. 湖南工业大学 理学院， 湖南 株洲 412007；2. 湖南工业大学 冶金工程学院，湖南 株洲 412007）

为了研究具有有界外部干扰的耦合谐振子网络的一致性，先利用变结构控制方法提出具有有界外部干扰的耦合谐振子网络的一致性协议；再运用Lyapunov稳定性理论、代数图论和矩阵理论，得到谐振子网络实现一致的充分条件；最后利用数值模拟验证提出协议的有效性。

外部干扰；耦合谐振子；一致性

0 引言

随着科学技术的发展，控制系统的结构和对象越来越复杂，网络和系统的协调控制得到了人们的高度关注。如：无人机飞行的编队控制，多智能体系统群集运动，分布式传感器网络控制，多机器人编队控制，人造卫星群位姿控制[1-5]等。

在多智能体系统的协调控制中，一致性（或同步）是重要的研究内容。由于耦合谐振子网络可以描述许多真实的自然现象，使得越来越多的学者对其一致性问题展开了讨论。

Kuramoto模型是一种比较典型的耦合谐振子模型。在文献[6]中，Y. Kuramoto提出实现网络一致性的基本条件是整个网络中的节点是全局连通的。在文献[7]中，Ren Wei研究了在网络连通受限的条件下，线性二阶耦合谐振子网络实现同步的问题，通过运用代数图论、矩阵理论等，得到网络实现同步的条件。文献[8]重点分析了在节点与邻居节点连通动态变化的网络中，耦合谐振子实现同步。文献[9]研究了非线性耦合谐振子的同步问题，运用一个非线性方程式描述节点之间的耦合关系。文献[10]在文献[9]研究成果的基础上进一步分析，从节点与邻居节点瞬时连通的角度，利用分布式控制协议，研究了耦合谐振子实现同步的问题。在文献[11]中，Zhang Hua等考虑了数据丢失的情况，研究了耦合谐振子网络同步问题。文献[12]提出了包含控制协议和基于采样数据的包含控制协议，研究了在有向拓扑下耦合谐振子网络的包含控制一致性问题。

许多学者从多个方面研究了耦合谐振网络的一致性问题，但他们没有考虑在有外部干扰的情况下，耦合谐振子网络如何实现一致性的问题。近年来，多智能体系统的理论研究发展迅速，节点与节点之间。节点与环境之间都会有密切联系和大量信息交换，如何抑制干扰让系统达到一致性，已经成为一个非常重要的现实问题。因此，本文研究具有有界干扰的耦合谐振子网络的一致性，并运用代数图论、矩阵理论以及Lyapunov稳定性理论，得到网络实现一致性的充分条件。

文中用到的符号有：Rn表示n维欧式空间；,和分别表示一个矢量的1-范数、2-范数和∞-范数；表示张量积；In是n阶单位矩阵。

1 预备知识和模型

2 具有有界干扰的耦合谐振子网络的一致性

3 数值仿真

为了说明前文所提出控制协议的有效性，本章考虑一个由8个谐振子组成的网络，对该网络进行数值仿真，此谐振子网络的拓扑结构见图1。

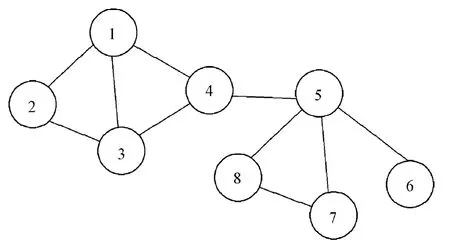
图1 谐振子网络的拓扑图Fig.1 The topology of harmonic oscillators network

该谐振子网络的拓扑图对应的邻接矩阵A=[aij]和拉普拉斯矩阵L=[lij]分别为：

本文选取谐振子的频率 =3，设定虚拟领导者的位置和速度为p0(0)=0.4，q0(0)=1。网络中的所有谐振子的速度和位置的初始状态都是随机的，其中8个谐振子中只有1, 5, 6谐振子可以收到虚拟领导者发出的信号，得到的网络速度轨迹和位置轨迹的仿真结果见图2～3。

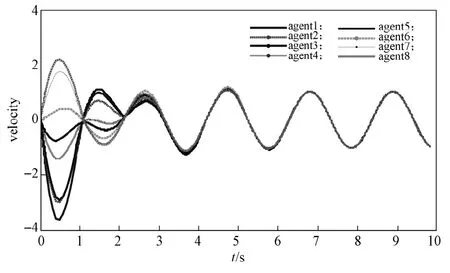
图2 仿真网络速度轨迹Fig.2 The velocity trajectory of simulated network

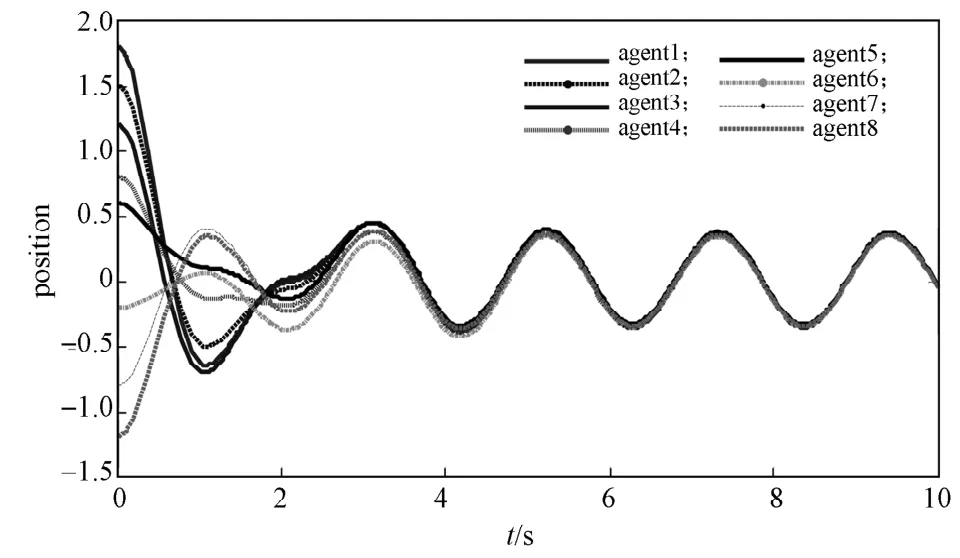
图3 仿真网络位置轨迹Fig.3 The position trajectory of simulated network

由仿真图可知，网络中所有谐振子在受到控制协议式（2）的控制下，可以跟踪到虚拟领导者的速度和位置，最终实现谐振子网络的一致性。

4 结语

本文研究了具有有界干扰的谐振子网络的一致性问题。提出了谐振子网络实现一致性的控制协议，并运用Lyapunov稳定性理论、代数图论和矩阵理论，得到了网络实现一致性的充分条件。最后通过数值仿真验证了所提出的一致性协议的有效性。

参考文献：

[1]Jadbabaie A，Lin J，Morse A S. Coordination of Groups of Mobile Autonomous Agents Using Nearest Neighbor Rules[J]. IEEE Transactions on Automatic Control，2003，48(6)，988-1001.

[2]郭 雷，许晓鸣.复杂网络[M].上海：上海科技教育出版社， 2006：247-248. Guo Lei，Xu Xiaoming. Complex Networks[M]. Shanghai：Shanghai Scientific & Technological Education Publishing House， 2006：247-248.

[3]Fax J A，Murray R M. Information Flow and Cooperative Control of Vehicle Formations[J]. IEEE Transactions on Automatic Control， 2004，49(9)：1465-1476.

[4]Kawasaki H，Ueki S，Ito S. Decentralized Adaptive Coordinated Control of Multiple Robot Arms Without Using a Force Sensor[J]. Automatica，2006，42(3)：481-488.

[5]Lu Xiaoqing，Francis Austin，Chen Shihua. Cluster Consensus of Second-Order Multi-Agent Systems via Pinning Control[J]. Chinese Physics B，2010，19(12)：120506.

[6]Kuramoto Y. Chemical Oscillations, Waves and Turbulence [M]. Berlin：Springer Verlag，1984：99-103.

[7]Ren Wei. Synchronization of Coupled Harmonic Oscillators with Local Interaction[J]. Automatica，2008，44(12)：3195-3200.

[8]Su Housheng，Wang Xiaofan，Lin Zongli. Synchronization of Coupled Harmonic Oscillators in A Dynamic Proximity Network[J]. Automatica，2009，45(10)：2286-2291.

[9]Cai Chaohong，Tuna S E. Synchronization of Nonlinearly Coupled Harmonic Oscillators[C]//American Control Conference. Baltimore：IEEE， 2010：1767-1771.

[10]Zhou Jin，Zhang Hua，Xiang Lan， et al. Synchronization of Coupled Harmonic Oscillators with Local Instantaneous Interaction[J]. Automatica， 2012，48(8)：1715-1721.

[11]Zhang Hua，Zhou Jin. Synchronization of Sampled-Data Coupled Harmonic Oscillators with Control Inputs Missing [J]. System & Control Letters，2012，61(12)：1277-1285.

[12]Xu Chengjie，Zheng Ying，Su Housheng，et al. Containment Control for Coupled Harmonic Oscillators with Multiple Leaders Under Directed Topology[J]. International Journal of Control，2015，88(2)：doi:10.1080/00207179.2014. 944873.

[13]Horn R A，Johnson C R. Matrix Analysis[M]. Cambridge：Cambridge University Press，1985：286-332.

[14]Su Housheng，Rong Zhihai，Chen M Z Q，et al. Decentralized Adaptive Pinning Control for Cluster Synchronization of Complex Dynamical Networks[J]. IEEE Transactions on Cybernetic，2013，43(1)：394-399.

[15]Slotine J J E，Li Weiping. Applied Nonlinear Control[M]. Beijing： China Machine Press，2006：51-62.

（责任编辑：邓光辉）

The Consistency of Coupled Harmonic Oscillator Network with Bounded Disturbance

Fan Longyun1，Zhu Shanhua1，Xu Chengjie1，Wen Ping2，Wen Wei1

（1. School of Science，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. School of Metallurgical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

For investigating the consistency of coupled harmonic oscillator network with bounded external disturbances，firstly proposed the consensus protocol by using the variable structure control method; Secondly based on Lyapunov stability theory, algebraic graph theory and matrix theory, obtained sufficient conditions for realizing the network consistency. Finally, used numerical simulation to verify the validity of the proposed protocol.

consensus；coupled harmonic oscillators；external disturbances

TP13；O322

A

1673-9833(2015)05-0102-05

10.3969/j.issn.1673-9833.2015.05.021

2015-07-09

湖南省普通高等学校教学改革基金资助项目（湘教通[2014]322），湖南工业大学自然科学研究基金资助项目（2014HZX23）

范龙云（1990-），女，河北高碑店人，湖南工业大学硕士生，主要研究方向为网络化系统控制，E-mail：fanlongyun125@126.com