FRP-混凝土粘结系统界面强度模型评估及其改进

童谷生

（华东交通大学土木建筑学院，江西 南昌330013）

FRP-混凝土粘结系统界面强度模型评估及其改进

童谷生

（华东交通大学土木建筑学院，江西 南昌330013）

采用文献中的FRP-混凝土粘结单剪试验的232组试验数据对5个界面粘结强度模型及相应的界面断裂能进行了简化的统计评估；对其中的Dai模型界面断裂能及粘结强度模型进行了修正和重新评估，修正后的模型可以用来较准确地估算界面断裂能及界面粘结强度。6个模型预测界面粘结强度模型计算分析表明：理论与试验值都有较好的线性相关性，但也有一定的分散性；基于非线性断裂力学的界面断裂能可以作为评估粘结强度模型是否合理的一个辅助手段。

FRP,混凝土；界面；粘结强度；断裂能

在FRP-混凝土外粘贴加固中，中部裂缝（IC）引起的界面剥离是受弯构件加固中的一种常见脱粘破坏模式。普遍认为，这类脱粘问题可以理想化为FRP与混凝土搭接接头来试验模拟[1-2]：即单剪、双剪和弯曲试验式的接头可以近似于二型界面断裂。尽管目前标准没有统一，但单剪实验易于实施，因此较多研究倾向于用单剪实验来模拟IC脱粘，其原理如图1所示。单剪试验是将FRP粘贴于混凝土柱体的一侧表面，在约束柱体位移的情况下使纤维板（布）受拉伸；测试内容包括FRP与混凝土界面的相对滑移，测试脱粘极限荷载(粘结强度)，通过试验分析与脱粘失效有关的控制变量尤其是强度模型。但由于材料与几何的不均匀与不连续性，这些强度模型一般在试验基础上通过拟合一些经验参数得到；因此可靠性需要大量数据来检验。

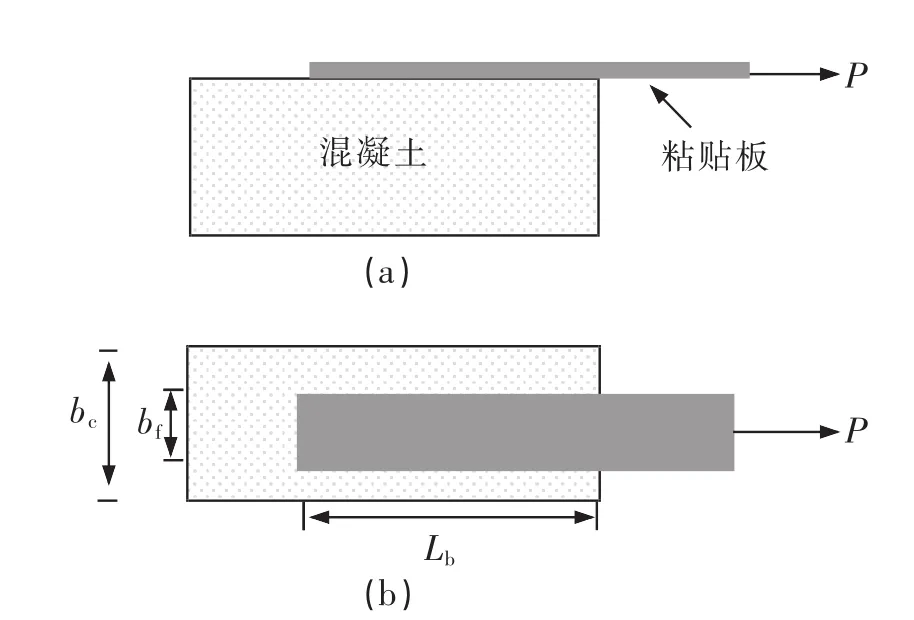
图1 单面搭剪试验试样(a)侧视图(b)俯视图Fig.1 Single-lap shear test specimen(a)side view(b)top view

通过试验研究，可以分析脱粘机理并定量研究影响粘结强度的几何与物理变量[3-6]，也通过界面相对滑移的测试来建立粘结滑移本构关系[7-8]，为加固结构计算和设计奠定基础。利用断裂力学进行分析，可以确定界面断裂能等关键的失效控制参数[4]。国外，有少量的研究对已有的模型进行评估[9-10]，通过评估可以了解各模型的接近程度和误差。但国内这方面工作未见报道，另外就是对界面强度或有效粘接长度进行评估,没有对断裂能进行评估，因此模型的可靠性论证不够充分。

本文对现有的5个较受认可的粘结强度模型利用文献中的232组单剪试验结果进行评估；在此基础上对其中原考虑柔性胶层特性的Dai模型进行修正，对修正后的模型进行重新评估，并验证其准确性。利用界面断裂能的概念对5个模型的界面断裂能的理论值与试验值的比进行评估，分析各种试验值与估算值在统计意义上的差异，供加固设计的研究参考。

1 现有的部分FRP-混凝土粘结强度分析模型

现有的粘结强度模型有不下20个，其中有些模型考虑了有效粘结长度的影响，有些模型则没有考虑这一长度。本文下面的评估分析中主要考虑了Fib[11]，Cheng-Teng[12]，Wu[13],Seracino[14]及Dai[15]模型对整理出的文献中的实验结果进行评估。基于完整性考虑、下面给出相应的强度模型及简单分析相关的理论依据。

1)Fib模型

Fib模型[11]采用的是如下界面粘接强度估算表达式

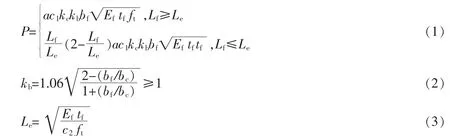
这里，P，Lf及Le分别是脱粘荷载、FRP粘结长度和有效粘结长度；bf，tf及Ef分别是FRP的宽度、厚度与弹性模量；ft是混凝土的柱体拉伸强度；α是考虑裂缝倾斜的缩减因子，近似取0.9，kc是考虑混凝土密实状态的因子，一般可以取1；kb是由方程(1b)给出的考虑FRP与混凝土相对宽度影响的几何因子；c1和c2是由实验核定的系数，对CFRP建议取0.64和2.0。

2）Cheng-Teng模型

Cheng-Teng[12]模型也是建立在有效粘接长度的基础上，脱粘荷载（粘接强度）以及FRP有效粘接长度可以由下式给出

3)Wu等人模型

Wu等[13]给出了层板结构基础上的基于断裂力学理论的脱粘荷载模型，该模型不涉及有效粘结长度。给出的理论结果为

其中：βw与式（5）相同，而，Gcf取0.17 N·mm-1

4)Seracino等人模型

Seracino等人[14]模型给出的脱粘荷载与FRP有效粘结长度由下式给出

这里，Af是FRP横截面面积；df是垂直于混凝土表面的失效平面的厚度，对外贴（EB）情况，取1mm；LPer是失效平面的长度，对外贴情况取2 df+bf，τf与δf是峰值应力和相应的滑移的估算式。

5)Dai等人模型

Dai等人[15]模型由下式给出脱粘荷载，以下表达式隐含了假定FRP足够长，后来尽管他们给出了有效粘结长度的表达式，但文献中仍较少采用，因此可认为与有效粘结长度无关的强度模型。

6)本文修正的Dai模型

通过计算发现（具体结果后面给出），Dai模型与其它4个模型不同，用该模型估算的粘结强度平均值约大33%，即界面断裂能偏大，因此本文对其进行了修正，修正后的模型只要对界面断裂能的系数修正为0.25，且不必在强度模型前加经验系数7.4便可以进行很好地预测，即修正后的界面断裂能和粘接强度模型如下

式（15）即为众所周知的Taljsten[23]得到的基于非线性断裂力学的粘接强度计算结果。后续的很多理论模型都是在此基础上的修正。

7）界面断裂能

界面断裂能可以通过界面粘接剪应力与FRP-混凝土之间的粘接滑移关系曲线下的面积来定义，直接利用这种定义来计算界面断裂能需要精确测试计算得到精确的粘接-滑移关系或至少得到其重要的影响参数[4-5]。但正如文献[4]所指出，很多模型通过试验或计算[8]得到界面断裂能都最后拟合成了表层混凝土或粘结胶层的特性，因此计算出的界面断裂能相差1-5倍以上[4]，在工程应用中要选择其中的某一个粘结强度就要反过来先确定用哪一个断裂能模型，因此很难说哪一个是准确的。本文利用Taljsten[23]给出的式（14）（15）来反算界面断裂能，则界面断裂能可以表示成下式：

下面的评估分析中，要利用的只是文献中材料性能数据以及试验荷载与各模型计算的荷载来评估各模型界面断裂能的总体差异,即各模型的真正意义上的断裂能应正比于荷载的平方。

2 实验数据来源

在本文中收集到的试验数据来自参考文献[7]及[16-22],文献[7]中应用的是原文作者Ko等的实验得出17组数据以及文献Carlo等人的14组数据。参考文献[16]整理了共有150组数据，由于篇幅所限没有将原数据出处一一列出。其它51组数据来自文献[16-22]。

3 强度模型及界面断裂能的评估方法

每一个强度模型的精确性依赖于模型估算值与实验值的比较。为了描述整体的精确程度，这里借助于数学中随机变量的描述方法，将单个实验值与对应的理论预测值用变量xi来表示：

其中：Pexp,i与Pth,i分别表示粘结强度的试验值与理论值；变量xi表示它们的比值。简化分析中可认为它是一随机变量，当它的均值接近于1，标准差与变异系数越小，表示该模型的准确程度越高；当均值大于1表示实验值总体小于理论值，是保守的估算，而当均值小于1表示实验值整体上要小于理论值，因此估算值偏于不安全。另外，还进行了实验值与理论值的相关性评估，相关系数越大表明总体趋势上物理变量之间线性关系也好，理论预测与实验结果相关性越强。

对界面断裂能的评估则由式（16）入手，则计算界面断裂能的试验值与理论计算值之比可以反映能量的统计结果：

能量值比的均值接近于1表示从能量考虑，两者更接近，而大于1表示愈保守。

4 结果和讨论

1）粘结强度预测与统计

利用前面所列的粘结强度评估算法，利用matlab编程可以计算232组数据的试验值与各个模型的预测结果及统计分析结果。粘结强度的实验与理论统计结果见表1，这里安全次数指理论值与试验值不小于1的次数。几个模型的理论值与试验值的对比还可以见图2，其中的相关系数也在图中标出。各模型界面断裂能的平均值及相关系数列于表2。

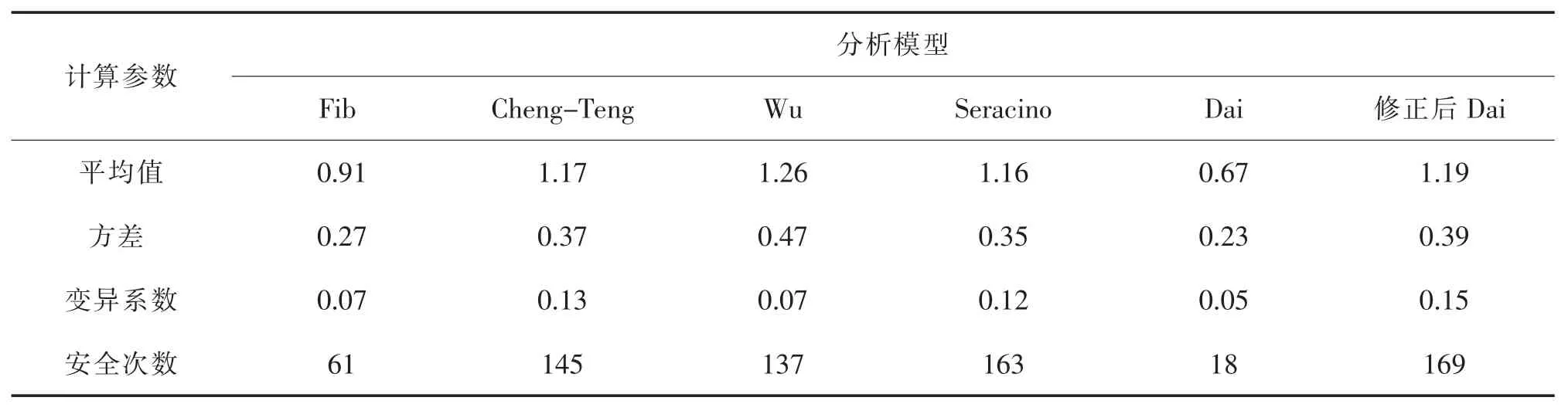
表1 粘结强度实验值与估算值计算统计结果Tab.1 Results of the statistical analysis in terms of coefficient variation and average value

从图2及表2可见对于粘结强度而言，每一个粘结强度模型都有较强相关性，但同时也较为分散，本文尽管不是真正进行的概率意义上的统计分析，但仍可以看出，用几个模型估算出的结果与试验值仍有偏差，尤其像Dai模型尽管已经属于偏危险的非保守模型，用该模型估算的粘结强度大多数要高于试验值，但仍有18个样本的估算值低于试验值。Dai等人的模型主要是考虑工程中应用不多的软胶，因此认为不太适合用于估算界面特性，另外考虑胶层厚度等特性，而工程中胶层厚度是一个很难控制的参数，有些分析中不把它作为一个强度估算模型[8]。但从本文修正后的模型的计算结果看，Dai模型中的界面断裂能反应了界面层胶的某些特性对断裂能的影响，只是较高地估算了常用结构胶粘结后的界面断裂能。从表2可见，用Fib模型比Dai模型总体上是偏于不安全的。

图2 粘结强度试验值与不同模型理论值的比较Fig.2 Comparison between experiment and different analytical values

表2 断裂能试验值与理论值比的均值及相关系数Tab.2 Results of the statistical analysis in terms of fracture energy ratio and coefficient

从界面断裂能的角度考虑，用Chen-Teng及Seracino模型和本文修正后的模型断裂能的理论值与试验值的比都和1较接近或大于1。容易验算修正后的模型中的界面断裂能（14)与陆新征[8]用精细有限元计算的大15%左右,且与文献[4]实测的结果更加接近。 当然，从工程方面考虑，从强度模型到设计模型只要在强度表达式前乘以1个小于1的系数就可以根据所需要的安全系数进一步修正，如Cheng-Teng模型建议将系数0.427改为0.375，则更改后的设计模型的粘接强度均值比改为1.34，能量比的均值变为1.66，样本中大于粘结强度试验值大于理论值的统计次数为198，但相关系数不变。另外，从表1与表2可见在粘接强度均值接近的情况下（表明有相同的安全储备），只要采用由本文使用的基于断裂力学的断裂能得表达式（16），断裂能就不会像文献[4]指出的5～6倍的差别。产生这种差别的原因是因为不同研究者采用的是不同的界面本构关系，而其中的材料不均匀和滑移测量采用的是不同精确度的方法所至。

6 结论

本文利用文献中的实验数据对现有的FRP/混凝土界面几个粘结强度的5个模型进行了评估，同时采用界面断裂能的概念对界面断裂能进行了评估，另外还对原来只适用于软胶层粘贴的界面断裂能及粘结强度模型进行了修正，得到了以下结论：

1）各模型都是根据自己的试验结果与前期的一些试验结果分析主要相关变量得出的近似结果，数据都有一定的分散性，且有些便于不安全，因此有些模型要用于设计需要在粘结强度除以较大的安全系数，因此仍需要更精确的模型来揭示其机理。

2）修正后的界面断裂能与陆新征的模型非常接近。

3）修正后的Dai等人的粘结强度模型与其它强度模型一样可以用来预测普通结构胶粘结后的粘结强度。

4）各种界面断裂能计算产生的差别可以通过非线性断裂力学得到的能量计算来复核，而不是通过粘结-滑移关系积分得到，这可以和粘结强度统计评估结合以确定模型的合理性。

[1]黄培彦，张术宽，等.FRP片材在土建修复加固工程中应用的力学问题[J].固体力学学报，2010，31（5）：440-450.

[2]腾锦光，陈建飞.FRP加固混凝土结构[M].中国建筑工业出版社，2004：11-26.

[3]HOSSEINI A,MOSTOFINEJAD D.Effective bond length of FRP-to-concrete adhesively-bonded joints:Experimental evaluation of existing models[J].International Journal of Adhesion Adhesives，2014（48）：150-158.

[4]彭晖，高勇.FRP-混凝土界面粘结行为的参数影响研究[J].实验力学，2014，29（4）：489-498.

[5]ObAIDAT Y T，HEYDEN S ET AL.Evaluation of parameters of bond action between FRP and concrete[J].Journal of Composites for Construction，2013，17（5）：626-635.

[6]TONG G S，CHEN S S.Prediction bond strength between FRP and concrete interface by LEFM method [J].Advanced Materials Research，2014（988）：195-200.

[7]KO H，MATTHYS S ET AL.Development of simplified bond stress-slip model for bonded FRP-concrete interfaces[J].Construction and Building Materials，2014（68）：142-157.

[8]LU，X Z，TENG J G，ET AL.Bond-slip models for FRP sheets/plates bonded to concrete[J].Engineering Structures，2005（27）：920-937.

[9]D’ANTINO T，PELLEGRINO C.Bond between FRP composites and concrete:Assessment of design procedures and analytical models[J].Composites:Part B，2014（60）：440-456.

[10]TOUTANJI H，SAXENA P ET AL.Prediction of interfacial bond failure of FRP-concrete surface[J].Journal of Composites for construction，2007（11）：427-436.

[11]FIB BULLETIN 14.Externally bonded FRP reinforcement for RC structures[M].Lausanne，Switzerland，2001.

[12]CHEN J F，TENG J G.Anchorage strength models for FRP and steel plates bonded to concrete[J].Journal of Structural Engineering，2001，127（7）：784-791.

[13]WU Y F，ZHOU Z Q，ET AL.On shear bond strength of FRP-concrete structures[J].Engineering Structures，2010，32：897-905.

[14]SERACINO R，RAIZAL S MR，ET AL.Generic debonding resistance of EB and NSM plate-to-concrete joints[J].Journal of Composites for Construction，2007，11（1）：62-70.

[15]DAI J，UEDA T ET AL.Development of nonlinear bond stress-slip model of fiber reinforced plastics sheet-concrete interface with a simple method[J].Journal of Composites for Construction，2005，9（1）：52-62.

[16]MASHREI M A，SERACINO R ET AL.Application of artificial network to predict the bond strength of FRP-to-concrete joints [J].Construction and Building Materials，2013（40）：812-821.

[17]BIZINDAVYI L，NEALE K W.Transfer lengths and bond strengths for composites bonded to concrete[J].Journal of Composites for Construction，1999，3（4）：153-160.

[18]SUBRAMANIAM K V ET AL.Width effect in the interface fracture during shear debonding of FRP sheets from concrete[J]. Engineering Fracture Mechanics，2007（74）：578-594.

[19]SUBRAMANIAM K V ET AL.An understanding of the width effect in FRP-concrete debongding[J].Strain，2011（47）：127-137.

[20]CARLONI C ET AL.Experimental determination of FRP-concrete cohesive interface properties under fatigue loading[J].Composite Structures，2012（94）：1288-1296.

[21]CARLONI C ET AL.Investigation of sub-critical fatigue crack growth in FRP/concrete cohesive interface using digital image analysis[J].Composites:Part B，2013（51）：35-43.

[22]PELLEGRINO C TINAZZI D ET AL.Experimental study on bond behavior between concrete and FRP reinforcement[J].Journal of Composite for Construction，2008（12）：180-189.

[23]TALJSTEN B.Strengthening of concrete prisms using the plate bonding technique[J].International Journal of Fracture，1996，82（3）:253-266.

Evaluation and Improvement on Interface Bond Strength Model of FRP-concrete Bond System

Tong Gusheng
（School of Civil Engineering and Architecture，East Ching Jiaotong University，Nanchang 330013，China）

Two hundred and thirty two groups of experimental results from published single-lap shear test specimens were used to evaluate the interface fracture energy and bond strength of FRP/concrete bond system. The five existing analytical models were evaluated by means of simplified statistical analysis.The model proposed by Dai was modified and reevaluated,which can predict the interface fracture energy and bond strength accurately.Analysis and calculation show that the six analytical bond strength values have good linear correlation with the experimental data but with different accuracy and dispersion.The evaluation of interface fracture energy based on nonlinear fracture mechanics can be used as an auxiliary means of rationality assessment.

FRP;concrete;interface;bond strength;fracture energy

TU313

A

1005-0523（2015）06-0054-07

（责任编辑 王建华）

2015－09-25

国家自然科学基金项目(11242006,11462005)

童谷生（1962—），男，教授，博士，研究方向为结构强度与加固设计。