双边带调幅方式时域波形相位突变的研究
2015-12-07郑贵金
郑贵金
(绥化学院电气工程学院 黑龙江绥化 152061)
双边带调幅方式时域波形相位突变的研究
郑贵金
(绥化学院电气工程学院 黑龙江绥化 152061)
文章针对双边带调幅方式时域波形相位突变问题进行了深入研究和详细解释,得出了相应结论:双边带调幅信号时域波形产生180°相位突变,但波形偶对称;双边带调幅信号时域波形产生180°突变,但波形奇对称;双边带调幅信号时域波形产生180°突变,但波形非对称。并通过Matlab仿真进行了验证。
双边带调幅;相位突变;Matlab仿真
通信电子电路、高频电子电路、非线性电子电路等课程是高等学校通信工程、电子工程等电子信息类专业重要的专业基础课,当前在此类教材中,关于双边带调幅方式中波形相位突变的问题大都粗略讲解,缺乏关于其深入全面的分析,本文将对双边带调幅方式波形相位突变给出细致分析。
假设高频振荡的载波电压为一余弦波,调制信号为一个单频率的余弦电压信号,分别表示如下
其中Vcm为载波振幅,Fo为载波频率,φ为初始相位,VΩm为调制信号幅度,fΩ为调制信号频率。
经过抑制载频的双边带调制之后,已调波的数学表达式为
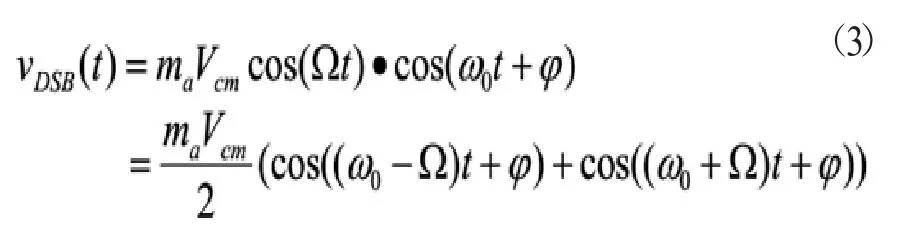
已知载波频率f0远远大于调制信号频率fΩ,调制信号vΩ(t)一个周期内包含多个载波信号周期。双边带调幅信号是调制信号与载波信号相乘的结果,其波形幅度仍随调制信号变化,但它的包络不再反应调制信号的形状,而是在过零点相位产生突变。在调制信号的正半周,双边带调幅信号与载波信号同相位;在调制信号的负半周,双边带调幅信号与载波信号反相位。而载波信号波形始终是相位连续的,所以在低频的调制信号时域波形的过零点处(从正到负,或从负到正),双边带调幅信号波形会产生180°相位突变。双边带调幅波信号相位突变现象导致的波形变化会因参数设置不同而不同,主要取决于f0与fΩ之间的比例关系以及初始相位的值。
双边带调幅波信号波形相位突变现象大致分为以下三类情形:
一、双边带调幅信号时域波形产生180°相位突变但波形偶对称
(一)初始相位φ=0或π时,令f0=kfΩ,k是非负数。当k为奇数,即(k=1,3,5,7,9,11,13,15,...)时,双边带调幅信号波形始终在过零点存在180°相位突变,如图1和图2所示。因为此时调制信号VΩ(t)一个周期内恰好包含奇数个载波信号Vc(t)周期,调制信号VΩ(t)的过零点与载波信号Vc(t)的过零点总是重合。且在调制信号的过零点处,调制信号关于过零点是奇对称的,而载波信号关于此点也是奇对称的,所以由调制信号与载波信号相乘得到的双边带信号关于此点是偶对称的。图1表示φ=0,图2表示φ=π。
(三)初始相位时φ≠0,令f0=kfΩ,k是非负数。当k>1且非整数时,设k的整数位的值为m,小数位的值为n,即k=m+0.n。在调制信号的过零点处,载波相位为,此时,若m为奇数,且,……)或者若m为偶数,且(n=0,1,2,3,……),从而归纳为上述两种情况,调制信号的过零点与载波信号的Vc=(t)过零点总是重合且波形偶对称。
举例验证:用Matlab仿真工具验证上述结论。
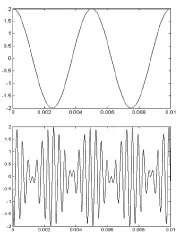
图1
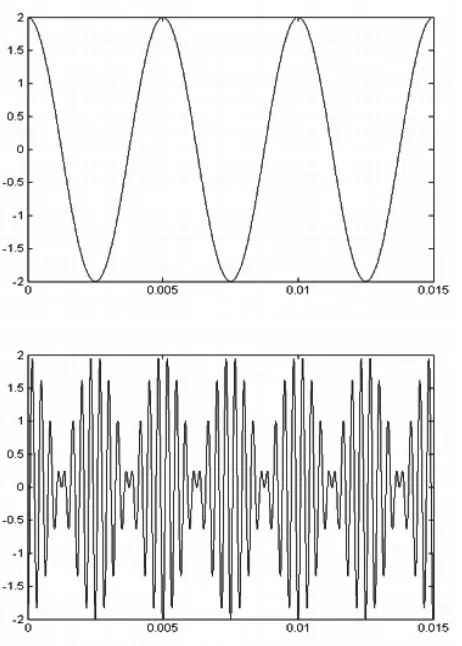
图2
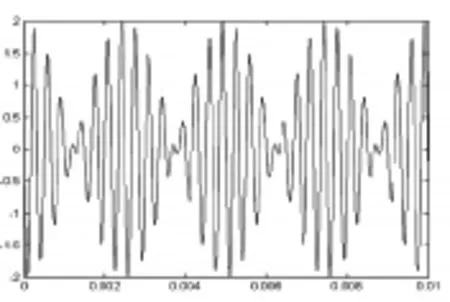
图3
二、双边带调幅信号时域波形产生180°突变但波形奇对称
(一)初始相位φ=0或π时,令f0=kfΩ,k是非负数。当k>1且k为正偶数即(k=2,4,6,8,10,12,14,...)时,双边带调幅信号波形始终在过零点存在180°相位突变,如图4所示。此时尽管调制信号VΩ(t)一个周期内包含偶数个载波信号Vc(t)周期,但调制信号VΩ(t)的过零点与载波信号Vc(t)的过零点不重合。且在调制信号的过零点处,调制信号关于此点奇对称,而载波信号在此点到达波峰(或波谷),关于此点是偶对称的,所以由调制信号与载波信号相乘得到的双边带信号关于此点是奇对称的。
(三)初始相位时φ≠0,令f0=kfΩ,k为非负数。当k>1且非整数时,设k的整数位的值为m,小数位的值为n,即k=m+0.n。在调制信号的过零点处,载波相位为,此时若m为偶数,且或者若m为奇数且(N=0,1,2,3,……),从而归结为上述两种情况,在调制信号VΩ(t)的过零点处,载波信号Vc(t)波形到达波峰(或波谷)从而双边带调制信号奇对称。
举例验证:用Matlab仿真工具验证上述结论。
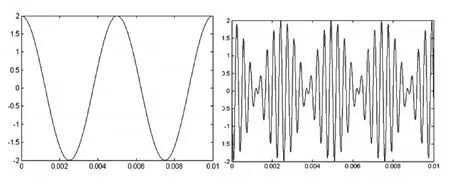
图4
三、双边带调幅信号时域波形产生180°突变但波形非对称
初始相位为φ,令f0=kfΩ,k为非负数。
把k写成k=m+0.n的表达式(m为k的整数位的值,n 为k的小数位的值;k为整数时,k=m,n=0),在调制信号的过零点处,载波相位为φ+Φ=φ+0.n×(Ωt)。此时无论m为正奇数或正偶数,若φ+Φ≠Nπ且,双边带信号存在180°相位突变,但是在调制信号的过零点处,载波信号并非处于波形的零点,波峰或波谷中的任一点,所以双边带调制信号波形非对称(如图6所示)。
例 6 设 Ω=200rda/s,ω0=14.4Ω,φ=0.011π,vDSB(t)=2cos (400πt)·cos(14.4×400πt+0.011π),波形对应图6.
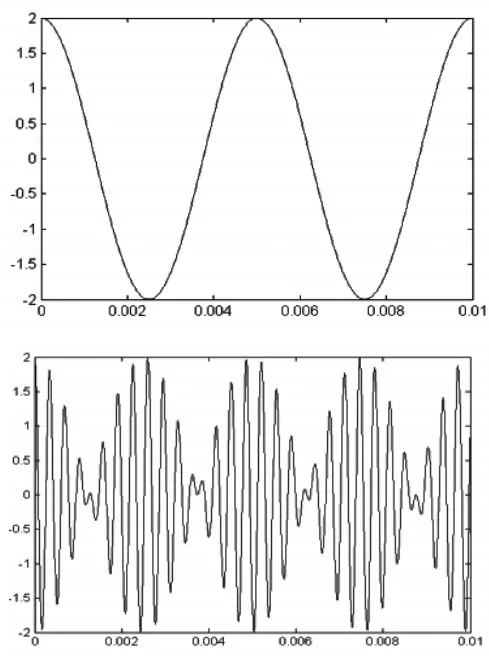
图5

图6
四、结束语
本文通过使用Matlab仿真软件,验证了文中关于双边带调幅方式时域波形相位突变问题的分析结论,并证明其正确性,这将有助于学生更深入透彻地理解振幅调制中双边带调制部分的内容,掌握双边带调幅方式时域波形相位突变的分析方法。对后续课程、频率调制和相位调制内容的学习也有很大帮助。
[1]张肃文.高频电子线路[M].北京:高等教育出版社,2009.
[2]刘彩霞,刘波粒.高频电子线路[M].北京:科学出版社,2008.
[3]樊昌信,曹丽娜.通信原理[M].北京:国防工业出版社,2009.
[4]黄智伟.调制解调器电路设计[M].西安:西安电子科技大学出版社,2009.
[责任编辑 郑丽娟]
TN 274
A
2095-0438(2015)12-0152-03
2015-08-27
郑贵金(1962-),男,黑龙江绥化人,绥化学院电气工程学院高级实验师,研究方向:电子技术。
黑龙江省高等学校教改工程项目(JG2014011118)。
