复杂工况单向固结理论分析及可视化

袁 颖,尹 超,周爱红

(石家庄经济学院勘查技术与工程学院,河北石家庄 050031)



复杂工况单向固结理论分析及可视化

袁 颖,尹 超,周爱红

(石家庄经济学院勘查技术与工程学院,河北石家庄 050031)

以Terzaghi单向固结理论为基础，对均质土层、分层土层、土层荷载增加、土层厚度变化情况下的孔隙水压力进行了理论分析。建立了以孔隙水压力为未知量的差分形式的控制方程，并通过泰勒级数展开，推导建立了具有二阶精度的边界方程；同时采用MATLAB软件编制相应的通用程序，得到Terzaghi单向固结理论孔隙水压力的数值解。此外，基于按作用消散的平均孔隙水压力的定义通过已经得到的孔隙水压力的数值解计算得到各不同复杂工况下的平均固结度，并且利用MATLAB软件强大的数值计算能力和图形处理功能，实现可视化，对于实际工程中的平均固结度的求解及通过平均固结度来推断地面沉降量有一定的指导和参考价值。

单向固结 复杂工况 MATLAB可视化 平均固结度

Yuan Ying, Yin Chao, Zhou Ai-hong. Analysis of complex conditions of one-dimensional consolidation theory and visualization[J]. Geology and Exploration, 2015, 51(5):0999-1006.

1 前言

Terzaghi(1925)建立了饱和土体单向固结微分方程，并获得均质土层、荷载瞬时施加条件下的初始条件和边界条件的数学解。但是，在实际的工况条件下，地基通常由多层土组成，各土层渗透系数、压缩系数各不相同，固结系数也不同，孔隙水压力的分布变化规律无法通过解析解计算得到，只能通过数值解的方法获得；此外，考虑到实际工程施工中建筑物的搭建是一个缓慢的过程，即外荷载是一个随时间逐渐增大的过程，与Terzaghi假设的荷载一次瞬时施加并不完全相同。因此，Terzaghi假定的情况在很多情况下难以满足。对此，早在上世纪90年代国内的一些学者曾做过大量的研究工作，不仅给出了层状地基一维和多维固结计算方法，同时也给出荷载随时间任意变化及起始孔隙水压力沿深度任意分布情况下双层地基一维固结解答(谢康和，1994；罗嗣海，1997)。进入21世纪以来，在岩土工程学科突飞猛进的发展下，国内岩土工程学者针对太沙基方程存在的各种局限性提出严格满足条件的修正方程，不仅得到连续排水面条件下精确解析解，同时还验证固结系数不是唯一决定固结性状的土性参数(江雯等，2003；梅国雄等，2008，2011；郑健龙等，2012)。此外，其他研究者使用ABAQUS有限元软件制作并开发连续排水边界Terzaghi一维固结解析解，表明有限元软件在地基固结方面的应用是十分可行的(蔡烽等，2012，2013)。但是在涉及区域问题计算时，比较有效的方法是直接对一维偏微分方程进行数值计算，此时，采用有限差分法会比较方便快捷(牛文杰等，2009；刘日成等，2012；段伟强等，2014；谢云跃等，2015)。使用有限差分法对外荷载变化情况和土层厚度变化情况进行求解时，每个微小时刻的初始条件和边界条件是变化的(介玉新等，2012；吴立松，2014)。

MATLAB软件作为新一代的数学软件和编程语言，在数据分析、数值计算及程序编制和可视化等方面拥有强大的优势，在边坡工程及采矿工程领域内，得到了广泛应用(王巧花等，2005；赵亚红等，2012；唐高朋等，2013)。本文针对均质土层、分层土、外荷载变化和土层厚度变化四种工况条件，采用有限差分法，基于MATLAB软件中的GUI模块开发了各工况的计算程序并实现了计算过程和数据处理的可视化，不仅得到各种工况条件下的孔隙水压力分布规律，同时还可以计算得到不同固结时间下的平均固结度，对实际工程施工中沉降的计算有一定指导意义。

2 Terzaghi单向固结理论及有限差分方程的建立

2.1 均质土层单向固结理论微分方程的建立

假设土体为粘土层，且底部不透水，仅顶面可排水，地面作用有均布荷载p，分布很广，故附加应力沿深度不变，其值为σ=p。

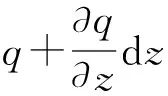
(1)

由于在固结过程中外荷载保持不变，因而在z深度处的附加应力σz=p也为常量(殷宗泽，2007)，则有效应力的增加等于孔隙水应力的减小，即

(2)

根据达西定律即可得到单向固结微分控制方程

(3)

其中,

(4)

(4)式中，Cv是土的固结系数，m2·d-1，它是反映超静孔隙水压力消散快慢的一个参数，Cv值高，单位时间内超静孔隙水压力的改变量变大。以下为了方便叙述，超静孔隙水压力简称为孔隙水压力。

网格剖分，建立待求差分模型，如图1所示。

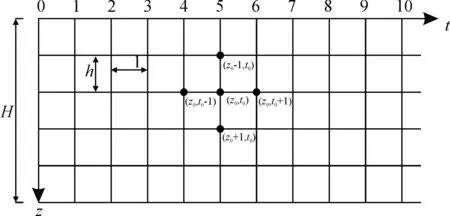
图1 土层网格剖分Fig.1 Grid subdivision of soil layer

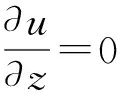
按照显示差分格式，可将(3)式表示如下：

(5)

由(5)式知，若已知前一时刻的孔隙水压力，则后一时刻的孔隙水压力均可由(6)式得到。

(6)

并注意到当Cvl/h2≤1/2时，(14)、(16)、(17)式才是数值稳定的。

根据上述显示差分公式，在计算边界上一内节点孔隙水压力时需要用到边界上孔隙水压力值。为计算边界处孔隙水压力值，将其临近2个内节点和1个关于边界对称的虚节点的孔隙水压力在边界点上进行泰勒级数展开，假定土层分为z层：

(7)

(8)

(9)

(10)

(11)

边界上孔隙水压力具有二阶精度。

2.2 成层地基单向固结理论微分方程的建立

土层成层分布，对于每一个分层都近似认为是均质的，同样可以按照(6)式来计算孔隙水压力。不同的是，在层面间应该满足连续条件，不同的层内应采用不同的分格尺寸或者不同的计算时段。

在分界面上的j0点，地下水渗流应符合连续条件，即进入界面的流速(李广信,2004)应当等于离开界面的流速，即

(12)

写成差分形式，则有

(13)

各分层内采用相同的分格尺寸，则Δz1=Δz2，可以将(13)式简化，如果再令k1=mk2，则(13)式可以写为

(14)

以上是在分层界面处的计算公式，过渡到第二层后，依然按照(6)式来进行计算。

2.3 外荷载逐渐增加单向固结理论微分方程的建立

地基土层为均质土层和分层土的情况下，外荷载都是一次瞬时施加在基础上，而建筑物在兴建过程中总会有一个过程。显然，这样的一个施工期内，孔隙水压力的产生和消散与荷载一次施加是有区别的，因此考虑荷载缓慢施加是很有必要的。

当荷载缓慢施加时，附加应力随时间变化，σz≠p，同时有

(15)

进而可以得到单向固结微分方程为

(16)

图2为外荷载随时间增加的情况。假设外部施加的荷载p为线性增加。将时间t划分为很多很小的时间间隔Δt，每个Δt的时间内外荷载线性增加量等价为阶梯增加量Δp，使之符合太沙基一维固结理论假设条件。结合(16)式单向固结微分方程、图1和图2，假设t时刻总应力为p(t)，则t+1时刻总应力为p(t+Δt)，每个时刻孔隙水压力消散的计算仍按照固结微分方程(16)式得到。

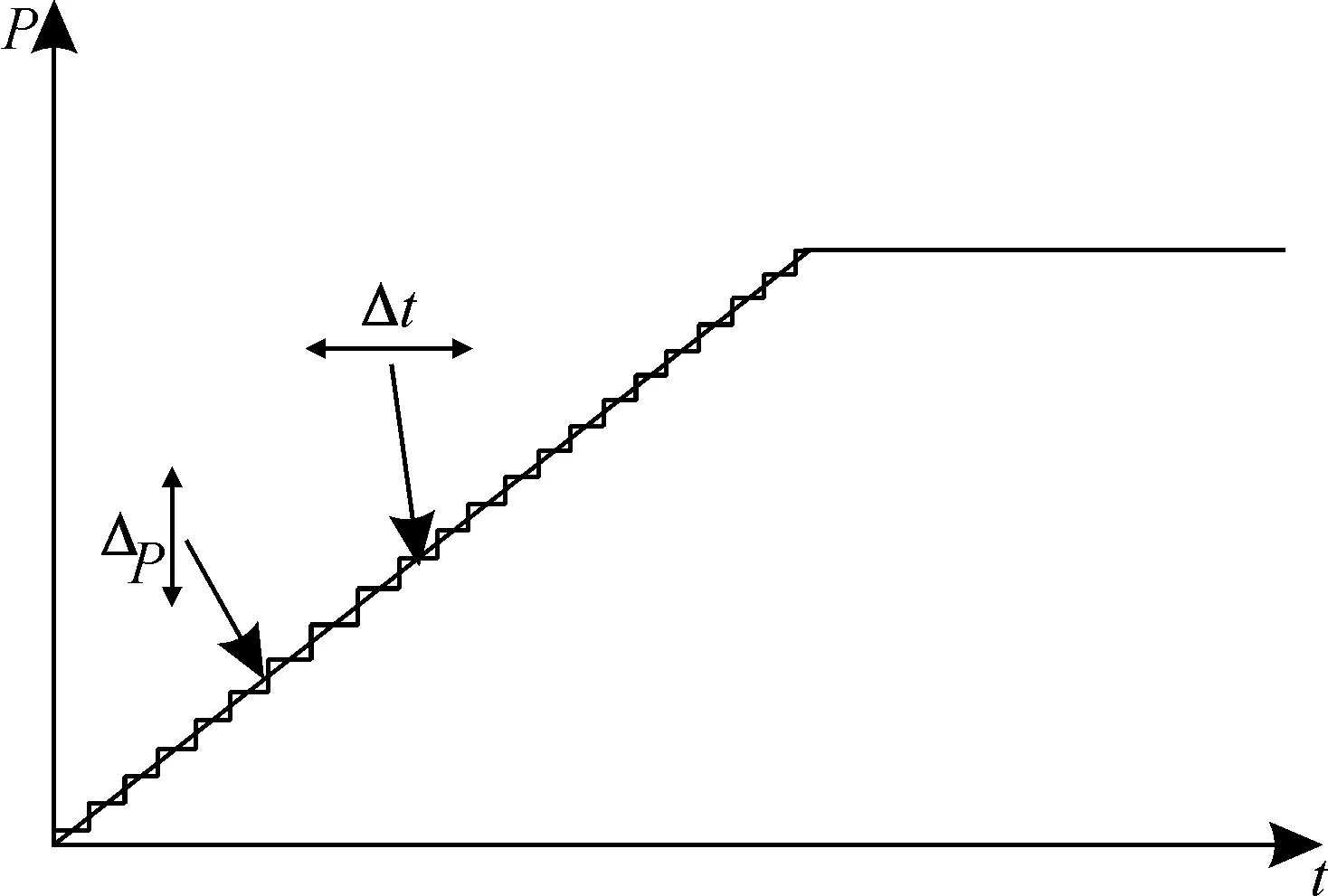
图2 外荷载随时间变化示意图Fig.2 Schematic diagram of external load varying with time

2.4 土层厚度逐渐增加单向固结理论微分方程的建立

在实际施工过程中针对路基填筑和堤坝填筑的情况，地基的土层厚度是随时间逐渐增加的，因此考虑土层厚度的变化是很有必要的。

由于外荷重增量Δσ=0，设渗透系数k=常量，土层厚度的增长规律是H=f(t)，建立土层厚度逐渐增加的单向固结微分方程

(17)

写成下面的差分形式

(18)

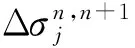
3 程序的设计与可视化

以程序的易用性为出发点，采取面向对象的编程方法，基于MATLAB可视化界面编辑器编程实现参数的可视化输入、计算结果与图像的可视化输出，可以给工程应用提供便利。

3.1 程序的设计

首先在网格剖分参数输入面板和常规参数输入面板内对应输入参数，确定设计参数是否满足约束条件(显示差分稳定条件为Cvl/h2≤1/2)，系统会对输入参数进行合理化判断(若满足则进行下一步，反之则提示输入正确的数值)，输入数据后系统自动运行程序，得到图像后可通过菜单栏的设置选项改变曲线并通过界面的控键来实现数据的输出和图形的存储，最后通过固结时间计算得到平均固结度，孔隙水压力变化及平均固结度的绘制程序设计的流程图如图3所示。

图3 程序流程图Fig.3 Program flow chart

3.2 程序的可视化

本程序界面主要有两个部分组成，引导界面和主界面。引导界面就是欢迎界面；主界面是指用户可在上面进行各种操作的界面。

运行程序，出现如图4所示的引导界面。

图4 程序引导界面Fig.4 Guidance interface of program

在引导界面上分别有四个按钮，根据实际情况判断属于哪种工况条件，点击进入相应的主界面上，如图5所示，以简单土层按钮为例，图中给出了差分解与理论解的对比，可以看出差分解的精度很高。

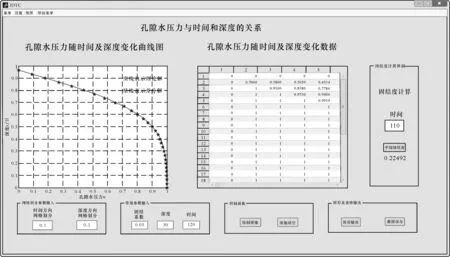
图5 程序主界面Fig.5 Main interface of program

本课题研究的是单向固结孔隙水压力与时间和深度间的关系。菜单栏处有四个选项分别为菜单、设置、视图和帮助。菜单选项可以保存图像和退出程序；设置选项下设有三个子菜单，分别为改变线颜色、改变线型和改变线宽。通过这些设置可以改变生成的图像的样式，以区分不同条件的曲线(例图6)；视图选项包括对图型移动、放大和缩小的操作；在本程序计算求解过程中，有任何的问题均可以点击帮助菜单来查询帮助，包括参数的选取、按钮的效果、图形的变化等。

通过在网格剖分参数输入面板内输入时间方向和深度方向的步长及在常规参数输入面板内输入的固结系数来判断是否满足显式差分格式的稳定条件，如果满足要求则可以绘制图像，否则应重新剖分网格。界面左侧的图型窗口可以得到满足稳定条件的图像，图形输出按钮可以将图像存储为图片格式。界面右侧的表格所对应的是每次生成不同曲线的数据，数据保存按钮可以将这些数据存储为excel文件。

为满足实际的工程中关于沉降计算的需要，求解平均固结度是非常有必要。本程序通过在固结度计算界面中输入不同的固结时间，可以得到对应时刻下的平均固结度。

4 计算结果与分析

各不同复杂工况的主界面均与图5类似，为清楚表达孔隙水压力分布和消散情况，设土层深度方向网格剖分为0.1m，时间方向网格剖分为0.1d，固结系数为0.03m2/d，土层厚度为10m；固结时间分别从0逐渐增加到60d、100d、140d和180d，无限均布荷载一次瞬时施加1kPa。另外，对于图6(b)，上层土渗透系数与均质土层一样，下层土为上层土渗透系数的1/4；对于图6(c)，荷载在0到180d内从0线性增大到1kPa；对于图6(d)，土层重量从0逐渐增大到1kPa。得到各工况不同时刻下的计算结果如图6所示。

图6给出了四种工况下孔隙水压力随时间和深度的变化曲线，随着时间增加，孔隙水压力逐渐消散，随着深度增加，孔隙水压力增大。由图6(b)可见，在0.6m处，即土层分层界面处，孔隙水压力产生明显的突变，曲线形状向内侧凹陷表明上层土层固结系数比下层土层的大，得到的结论符合假设条件。由图6(c)可见，同样的均质土层，当外荷载缓慢增加时，对比一次瞬时施加的荷载如图6(a)，孔隙水压力的消散要慢。图6(d)曲线形状与图6(a)曲线形状相似，但孔隙水压力消散的要快些。

图6 各种工况下孔隙水压力变化示意图Fig.6 Schematic diagrams of pore water pressure changes under various conditions(a)-均质土层；(b)-分层土层；(c)-土层上荷载变化； (d)-土层厚度变化(a)-homogeneous soil；(b)-layered soil；(c)-load increase on soil surface；(d)-change in soil thickness

图7 各工况下平均固结度的计算Fig.7 Calculation of average consolidation degrees under various conditions(a)-均质土层；(b)-分层土层；(c)-土层上荷载变化；(d)-土层厚度变化(a)-homogeneous soil；(b)-layered soil；(c)-load increase on soil surface；(d)-change in soil thickness

图7为各个工况相同固结时间下得到的平均固结度，反应孔隙水压力的消散程度。对比图7(b)和图7(a)可知，由于分层土下土层固结系数较小而上土层固结系数与均质土层一样，因此相同固结时间下的平均固结度较小，得到的结论也符合假设条件；图7(c)外荷载逐渐增加与图(a)荷载一次瞬时施加相比，相同固结时间的平均固结度较小，与定性分析的结论一样；对比图7(d)与图7(a)可知，随着土层厚度和重度的增加，相同固结时间下平均固结度较大，固结效果更快。

5 结论

(1) 基于太沙基单向固结理论，推导建立了以孔隙水压力为未知量的差分形式的控制方程和具有二阶精度的边界控制方程，采用有限差分法解决了复杂工况下难以求得解析解的情况，实现了对多种复杂工况下单向固结问题的数值计算。同时运用MATLAB软件开发了一款面向对象的单向固结软件，实现了孔隙水压力随深度变化的可视化。

(2) 建筑物或构筑物在施工和使用期间，常需了解沉降与时间的关系，即固结度，以便设计预留结构有关部分之间的净空、连接方法、施工顺序等。另外，当时间t趋于无穷，孔隙水压力完全消散，固结度趋于1时，计算得到的固结沉降即为最终沉降，可为地基基础设计提供依据。

(3) 对于很多工程实际，地基的固结问题严格意义上说属于二维甚至三维固结问题，孔隙水压力不仅与时间有关还与位移有关，采用比奥固结理论进行分析计算更为合理。但由于计算的复杂性，同时计算结果的合理与精确性很大程度上取决于计算参数的取值，因此限制了比奥固结理论在工程中的应用。太沙基固结理论在一维情况下是精确的，很多实际工程也可近似简化为一维固结问题进行分析，比如堤坝工程中在轴线上的固结、软土地基加固方法中的砂井预压法等。我国现行规范的主固结沉降也是采用太沙基一维固结理论。作者结合工程实际，进行了复杂工况固结理论及可视化方面的研究，同时，为了更好的指导工程实践，作者结合基金项目，目前正在进行单层土和多层土的固结物理模型试验，有望通过物理模型试验结果与本文程序的计算结果进行对比分析，比较计算结果与实际计算结果的误差，分析其原因并提出相应的改进方法。这也是作者下一步工作的内容。

Cai Feng, He Li-jun, Zhou Xiao-peng, Mei Guo-xiong. 2013. Finite element analysis of one-dimensional consolidation problem with continuous drainage boundaries in layered ground[J]. Journal of Central South University (Science and Technology), 44(1):315-323(in Chinese with English abstract)

Cai Feng, He Li-jun, Zhou Xiao-peng, Xu Mei-juan, Mei Guo-xiong. 2012. Finite element analysis of one-dimensional consolidation of undrained symmetry plane under continuous drainage boundary[J]. Chinese Journal of Geotechnical Engineering, 34(11):187-193(in Chinese with English abstract)

Duan Wei-qiang, Cui Shi-xin, 2014, Methodology of the safety evaluation for tailings dams[J]. Geology and Exploration, 50(4):783-788(in Chinese with English abstract)

Jiang Wen, Xie Kang-he, Xia Jian-zhong. 2003. The one-dimensional consolidation theory of heterogeneity foundation[A]. The Academic Conference Proceedings of 9th Conference on soil mechanics and Geotechnical Engineering, Chinese Civil Engineering Society[C] (Volume One). Beijing: Chinese Civil Engineering Society: 288-292(in Chinese)

Jie Yu-xin, Jia Zhi-jie, Chen Jie, Sun Tie, Li Xiao-ru. 2012. Difference method for analysis of consolidation in saturated foundation soil[A]. The Academic Conference Proceedings of 9th National Conferences on Engineering Geology, Engineering Geology Professional Committee of Chinese Geological Society[C]. Beijing:Engineering Geology Professional Committee of Chinese Geological Society: 223-227(in Chinese with English abstract)

Li Guang-xin. 2004. Advanced soil mechanics[M]. Beijing: Tsinghua University Press:275-287(in Chinese)

Liu Ri-cheng, Xu Bang-shu, Zhang Qin, Gong Ming. 2012. Finite difference numerical simulation of a foundation pit supported by double-row piles[J]. Geology and Exploration, 48(2):366-373(in Chinese with English abstract)

Luo Si-hai. 1997. Calculation and characteristics of layered ground[J]. Earth Science-Journal of China University of Geosciences, 22(2):91-95(in Chinese with English abstract)

Mei Guo-xiong, Xia Jun, Zhao Wei-bing, Zai Jin-min. 2008. Study on some problems about Terzaghi one-dimensional consolidation equation [A]. Port Engineering Chapter in Society of Chinese Civil Engineering, Seminar Proceedings of the 7th National Engineering Drainage and Reinforcement Technology[C]. Beijing: Port Engineering Chapter in Society of Chinese Civil Engineering: 62-69(in Chinese)

Mei Guo-xiong, Xia Jun, Mei Ling. 2011.Terzaghi’s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary[J]. Chinese Journal of Geotechnical Engineering, 33(1):28-31(in Chinese with English abstract)

Niu Wen-jie, Ye Wei-min, Huang Yu, Chen Bao. 2009. Analysis of drainage boundary effect on the consolidation rate from finite difference resolution for Terzaghi equation [A]. Society of Rock Mechanics in Jiangsu Province, Proceedings of the 6th Rock Mechanics and Engineering in Jiangsu Province[C]. Suzhou: Society of Rock Mechanics in Jiangsu Province: 92-96(in Chinese with English abstract)

Tang Gao-peng, Zhao Lian-heng, Li Liang, Gao Lian-sheng, Tan Han-hua. 2013. Program development for slope stability using MATLAB software and upper bound limit analysis[J]. Rock and Soil Mechanics, 34(7):273-280(in Chinese with English abstract)

Wang Qiao-hua, Ye Ping, Huang Min. 2005. Design of GUI based on MATLAB[J]. Coal Mine Machinery, 25(3):60-62 (in Chinese with English abstract)

Wu Li-song. 2014. Unidirectional consolidation to resolve complex situations under continuous boundary conditions[D]. Nanchang: Nanchang Hangkong University: 1-40(in Chinese with English abstract)

Xie Kang-he. 1994. Theory of one dimensional consolidation of double-layered ground and its applications[J]. Chinese Journal of Geotechnical Engineering, 16(5):24-35(in Chinese with English abstract)

Xie Yun-yue, Xiao Hong-tian, Yan Qiang-gang. 2015. Two-dimensional numerical simulation of macro-mechanical parameters for fractured rock masses[J]. Geology and Exploration, 51(2): 376-382(in Chinese with English abstract)

Yin Zong-ze. 2007. Soil Theory[M]. Beijing: China Water Conservancy and Hydropower Press: 315-316(in Chinese)

Zhao Ya-hong, Hao Yan-mian, Zhang Li-hua. 2012. Mining subsidence prediction and visualization based on MATLAB[J]. Coal Mining Technology, 17(1):93-95(in Chinese with English abstract)

Zheng Jian-long, Zhou Chi-qing, Zhang Jun-hui. 2012. Summary of 1-D consolidation characteristics of double-layered ground[J]. Journal of Changsha University of Science & Technology (Natural Sciences), 9(1):1-11(in Chinese with English abstract)

[附中文参考文献]

蔡 烽，何利军，周小鹏，梅国雄. 2013. 连续排水边界下成层地基一维固结问题的有限元分析[J]. 中南大学学报(自然科学版), 44(1):315-323

蔡 烽，何利军，周小鹏，徐美娟，梅国雄. 2012. 连续排水边界下一维固结不排水对称面的有限元分析[J]. 岩土工程学报, 34(11):187-193

段伟强，崔世新. 2014. 某上游式尾矿坝安全性评价方法分析研究[J]. 地质与勘探, 50(4):783-788

江 雯，谢康和，夏建中. 2003. 非均质地基一维固结理论[A].中国土木工程学会第九届土力学及岩土工程学术会议论文集[C](上册). 北京:中国土木工程学会:303-307

介玉新，贾志杰，陈 杰，孙 铁，李晓茹. 2012. 饱和土地基固结问题的差分法计算[A].中国地质学会工程地质专业委员会第九届全国工程地质大会论文集[C]. 北京:中国地质学会工程地质专业委员会:223-227

李广信. 2004.高等土力学[M]. 北京：清华大学出版社:275-287

刘日成，徐帮树，张 芹，公 铭. 2012. 深基坑双排桩结构支护效果有限差分数值模拟[J]. 地质与勘探, 48(2):366-373

罗嗣海. 1997.层状地基的固结计算与固结特性[J]. 地球科学-中国地质大学学报, 22(2): 91-95

梅国雄，夏 君，赵维炳，宰金珉. 2008. 关于太沙基一维固结方程若干问题的探讨[A].中国土木工程学会港口工程分会,第七届全国工程排水与加固技术研讨会论文集[C]. 北京:中国土木工程学会港口工程分会:62-69

梅国雄，夏 君，梅 岭. 2011. 基于不对称连续排水边界的太沙基一维固结方程及其解答[J]. 岩土工程学报, 33(1): 28-31

牛文杰，叶为民，黄 雨，陈 宝. 2009. 太沙基固结方程有限差分解分析排水边界对固结速率的影响[A].江苏省岩石力学学会,第六届江苏省岩土力学与工程学术大会论文集[C]. 苏州:江苏省岩石力学学会:92-96

唐高朋，赵炼恒，李 亮，高连生，谭悍华. 2013. 基于MATLAB的边坡稳定性极限上限分析程序开发[J]. 岩土力学, 34(7):273-280

王巧花，叶 平，黄 民. 2005. 基于MATLAB的图形用户界面(GUI)设计[J]. 煤矿机械, 25(3):60-62

吴立松. 2014. 单向固结的复杂情况在连续边界条件下的解析[D]. 南昌航空大学:1-40

谢康和. 1994. 双层地基一维固结理论与应用[J]. 岩土工程学报, 16(5):24-35

谢云跃，肖洪天，闫强刚. 2015. 裂隙岩体宏观力学参数的二维数值模拟[J]. 地质与勘探, 51(2):376-382

殷宗泽. 2007. 土工原理[M]. 北京:中国水利水电出版社:315-316

赵亚红，郝延锦，张丽华. 2012. 基于MATLAB的开采沉陷预计及可视化研究[J]. 煤矿开采, 17(1):93-95

郑健龙，周驰晴，张军辉. 2012. 双层地基一维固结特性研究综述[J]. 长沙理工大学学报(自然科学版), 9(1):1-11

Analysis of Complex Conditions of One-Dimensional Consolidation Theory and Visualization

YUAN Ying, YIN Chao, ZHOU Ai-hong

(SchoolofProspectingTechnology&Engineering,ShijiazhuangUniversityofEconomics,Shijiazhuang,Hebei050031)

Based on the Terzaghi one-dimensional consolidation theory, this paper analyses the pore water pressure in different cases including homogeneous soil, layered soil, load increase on the soil surface and variable soil thicknesses, The difference forms of governing equation in which the unknown quantity is pore water pressure have been established, Meanwhile, the boundary equations which have second-order accuracy are deduced through Taylor series expansion, Furthermore, the general program is developed using MATLAB software and the numerical solution of pore water pressure which is based on the Terzaghi one dimensional consolidation theory is obtained, In addition, the average consolidation degrees under different complex conditions are calculated through the numerical solution of pore water pressure based on the definition of average pore water pressure dissipated by different effects, Moreover, the visualization is implemented in terms of MATLAB software which has powerful functions of numerical calculation and graphic processing, These results have guiding significance and a reference value for solving average consolidation degrees and then evaluating land subsidence in practical engineering,

one-dimensional consolidation, complex conditions, MATLAB visualization, average consolidation degree

2015-03-15；

2015-08-10；[责任编辑]陈伟军。

国家自然科学基金(编号：41301015)、河北省教育厅自然重点项目资助(编号：ZD2015073)、石家庄经济学院国家自然科学基金预研基金(编号：syy201308)、石家庄经济学院学生科技基金(编号：KAY201508)联合资助。

袁 颖(1976年-)，男，2006年毕业于大连理工大学，获博士学位，教授，硕士生导师，主要从事工程地质方面研究工作。E-mail:yuanyingson@163.com。

TU431;TP319

A

0495-5331(2015)01-0999-08