无单元Galerkin法大地电磁三维正演模拟

李俊杰，严家斌，皇祥宇

(1.浙江省水利水电勘测设计院，浙江杭州 310002； 2.中南大学 地球科学与信息物理学院有色资源与地质灾害探查湖南省重点实验室，湖南长沙 410083)



无单元Galerkin法大地电磁三维正演模拟

李俊杰1，严家斌2，皇祥宇2

(1.浙江省水利水电勘测设计院，浙江杭州 310002； 2.中南大学 地球科学与信息物理学院有色资源与地质灾害探查湖南省重点实验室，湖南长沙 410083)

无单元Galerkin法(EFGM)作为一种相对成熟的无网格方法，避免了网格剖分，其精度高，适用于复杂电导率分布和复杂边界形状的计算。本文将EFGM用于大地电磁三维正演，详述了三维EFGM形函数的构造过程，从大地电磁三维变分问题出发，利用Galerkin法结合高斯积分公式推导了相应的系统矩阵离散表达式，简述了边界条件的加载技术，研究了支持域尺寸对EFGM三维正演计算精度的影响，最后通过数值计算验证了EFGM三维算法的正确性。

无网格法 无单元Galerkin法 大地电磁 支持域尺寸

Li Jun-jie, Yan Jia-bin, Huang Xiang-yu. Three-dimensional forward modeling of magnetotellurics using the element-free Galerkin method[J]. Geology and Exploration, 2015, 51(5):0946-0952.

作为网格法数值计算的重要补充和发展，无网格法是近十多年来兴起的一类数值计算新方法(Garbonetal.,2002；徐凯军等,2006；沈金松，2003；陈辉等，2011；刘长生等, 2010；Tongetal.,2009；Yangetal.,2013；Sunetal.,2014)，其形函数的构造避免了网格的生成过程, 物性加载在只与坐标位置有关的高斯点上，因此节点规则分布下也能计算复杂模型,现已成为力学领域的研究热点。无单元Galerkin法(Element-Free Galerkin Method，EFGM)是一种较成熟的拟合型无网格方法，其形函数的构造过程不存在奇异性问题,且能通过权函数的适当选取实现不同阶次的函数近似。p型自适应过程实现便利，不但广泛应用于有限元法所触及的领域，且成功解决了某些网格方法难以处理的问题(Belytschkoetal., 1994；Lietal., 2012；Liuetal., 2009),在地震波场(贾晓峰等,2006)、雷达波场(冯德山等,2013)、大地电磁场(李俊杰等, 2014a,2014b, 2014c, 2015；严家斌等，2014；Wittkeetal.,2014)及直流电法(李俊杰等,2015)二维响应的计算上也取得了成功。EFGM具有精度高、处理复杂模型便利等优势,然而有关EFGM在大地电磁三维正演中的应用还未见报导。

本文尝试将EFGM应用于MT三维正演，介绍了三维移动最小二乘(MLS)近似原理，推导了MT三维变分问题的EFGM总体矩阵表达式，简述了含背景网格的三维高斯积分技术，最后通过数值计算验证了EFGM算法的正确性。

1 大地电磁三维变分问题

当地下电性结构为三维时，取向东为x轴，x轴与y轴垂直，z轴垂直向下,求解域V为六面体区域，上下表面的4个顶点分别以A、B、C、D与E、F、G、H顺时针编号(图1)。

大地电磁三维正演满足式(1)的变分问题(Tongetal., 2009)：

(1)

图1 大地电磁三维模型Fig. 1 Three-dimensional MT model

2 大地电磁三维变分问题的无网格解法

2.1 支持域

EFGM利用位于高斯点支持域内的场节点构造形函数，支持域为高斯点附近人为划定的一个区域，其概念相当于FEM的单元,常用的支持域形状有球体与长方体两种。对于任一高斯点XQ，其支持域尺寸d由式(2)确定：

d=αdc

(2)

式中：α为支持域的无量纲尺寸，是对无网格法计算精度与效率影响很大的重要参数；dc为位于高斯点XQ附近的平均结点间距，可由式(3)确定：

(3)

式中：B为预估的支持域体积；n为包含在B中的节点数。对于节点均匀分布的情况，dc为节点间距。本文采用六面体支持域，故有三个方向的支持域尺寸，即式(4)：

(4)

式中：dcx、dcy与dcz分别为直角坐标系三个方的的节点间距；αx、αy与αz为对应的支持域无量纲尺寸。为便于程序设计，研究中常取αx=αy=αz=α，本文中取α=1.0,即支持域的大小与FEM单元相等。

2.2 移动最小二乘近似(moving least-square，MLS)

求解域Ω中任意一点X处的场变量u(X)的MLS近似表达式为：

(5)

式中：p(X)为三维空间坐标XT=[x,y,z]的基函数，可用Pascal三角形确定(赵熙强等, 2015)，其线性基函数为pT(X)={1xyz}；m为单项式的个数；a(X)是与高斯点位置相关的系数向量。MLS近似中的节点数通常大于基函数个数(n>m),系数向量a(X)需通过如式(6)的加权残差法求得：

(6)

式中W(X-Xi)为权函数，常用无网格权函数有三次样条函数、四次样条函数及指数函数(Belytschkoetal., 1994)。本文选择四次样条函数为权函数，表达式如式(7)：

(7)

式中：Ri=di/rω；di=|X-Xi|。di为节点Xi与高斯点X之间的距离，rω为权函数支持域尺寸。通过式(6)的运算将产生如式(8)的线性关系：

A(X)a(X)=B(X)Us

(8)

式中：Us={u1u2…un}T为支持域内所有节点的节点场函数向量，A(X)与B(X)表达式如下：

(9)

B(X)=[W1(X)p(X1)W2(X)p(X2)…Wn(X)p(Xn)]

(10)

式(9)中Wi(X)=W(X-Xi),求解式(8)可得：

a(X)=A-1(X)B(X)Us

(11)

将上式代入式(5)得：

φiui=ΦT(X)Us

(12)

ΦT(X)即为计算点X在支持域内的MLS形函数，其表达式为：

2.3 无网格离散系统方程的构造

将计算点处E的三分量Ex、Ey、Ez表示为形函数与场节点之积的形式，有：

(14)

式中：Φ为MLS近似构造的形函数矩阵；n为支持域内的节点数；Ex、Ey与Ez为支持域内n个节点的场向量。将式(14)代入式(1)有：

(15)

利用式(15)将式(1)最终表示为式(16)的形式：

δEKE=δE(K1+K2+K3)E=0

(16)

式(16)即为EFGM三维系统方程。

K的表达式中包含对求解域V与求解域边界面Γ的积分，为计算这些积分，一般将求解域离散成一组背景网格，以K1与K2矩阵左上角的元素为例,其积分可表示成单元积分之和的形式，有

(17)

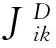
求解线性方程组KE=0还需加载边界条件。EFGM边界条件可用罚函数法加载，将刚度矩阵中相应的对角元素KII变为αKII，α为罚系数，其值可取104～1010,然后将边界上的E值取代方程组右端的零向量即可。

3 数值计算

为了验证EFGM算法的正确性，本文计算了若干数值模型：模型一为ρ1=1000Ω·m的均匀介质模型,用于支持域无量纲尺寸最优参数值的试验, 采用(11×11×66)个场节点，(10×10×65)个背影网格，节点间距为100m,空气层厚度为500m。模型二(图2)为二层介质模型，第一层电阻率ρ1=1000Ω·m，层厚h1=3km；第二层电阻率ρ2=10Ω·m，层厚h2=3km,空气层厚度及节点分布情况与模型一相同；模型三(图3)为六面体低阻模型，背景电阻率为1000Ω·m,异常体电阻率为10Ω·m,长宽高均为600m, 埋深800m，异常体中轴线的投影对应于求解域的原点，采用(41×41×46)个场节点，节点间距为200m。空气层厚度为1000m。

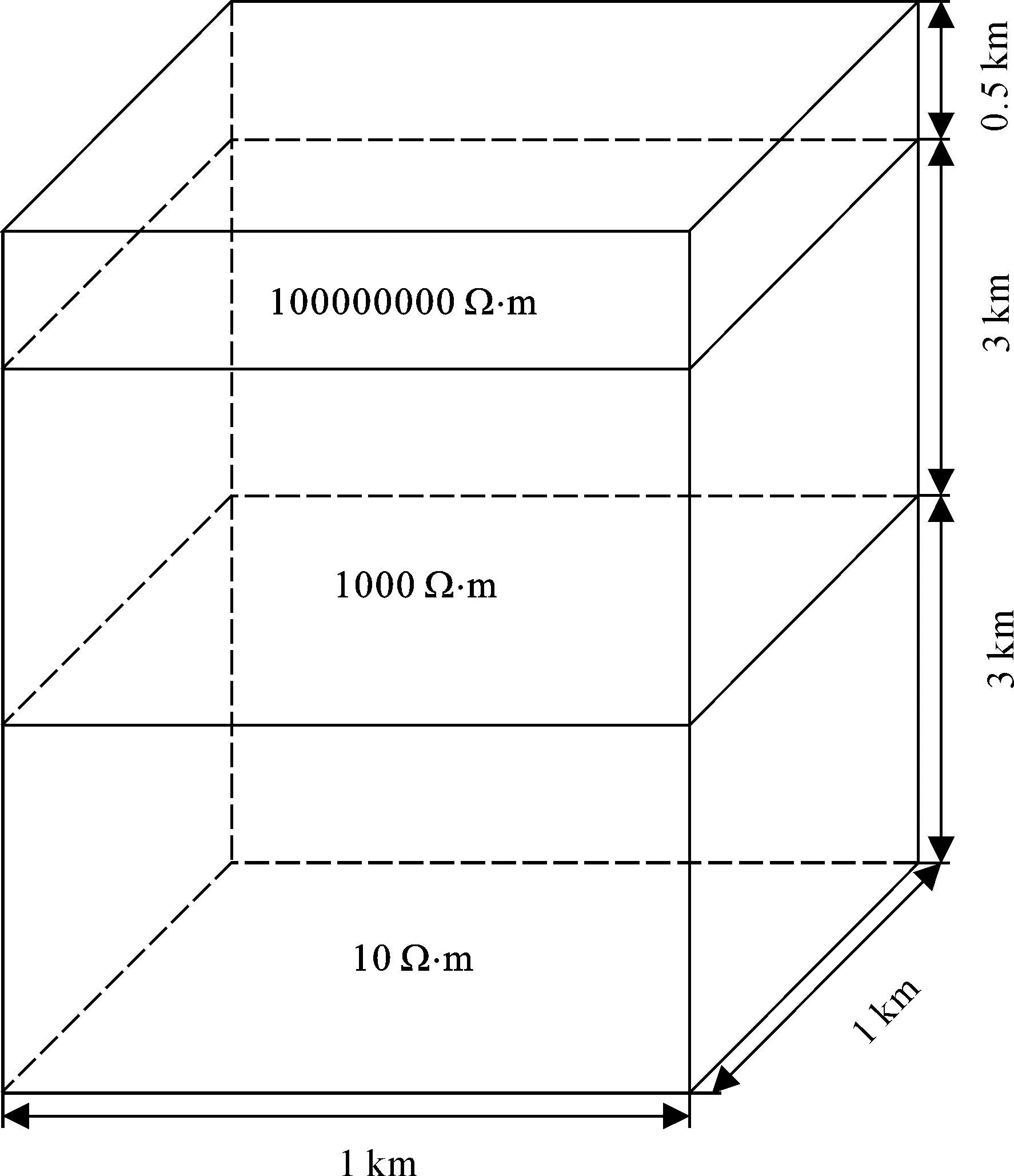
图2 模型二Fig. 2 model

图3 模型三Fig. 3 model 3

图4为不同支持域无量纲尺寸下模型一的EFGM计算结果。如图4所示,当支持域无量纲尺寸α=1～1.2时，计算结果与解析解基本一致,随着α的增大数值解开始偏离解析解，且α越大计算精度越低。数值试验过程中还发现当α>1.2时求解系统方程组的迭代次数会随着频率的增高而增大，当α>1.7时相同参数设置下计算结果开始发散。α增大的同时伴随着计算效率的降低，因此本文数值计算取α=1。

图5为二层介质模型的EFGM数值计算结果。如图5所示，EFGM计算结果与解析解基本一致, 验证了算法的正确性。图6 为频率f=10Hz时三维低阻模型的数值计算结果，视电阻率与阻抗相位断面图在中部区域呈现极小值，极小值的两侧附近呈现极大值,异常形态呈直立的椭圆形,背景区域的视电阻率接近1000Ω·m，阻抗相位接近45°(图6)，较好地反映出了地下异常体的存在，进一步凸显了EFGM在大地电磁三维正演中的有效性。

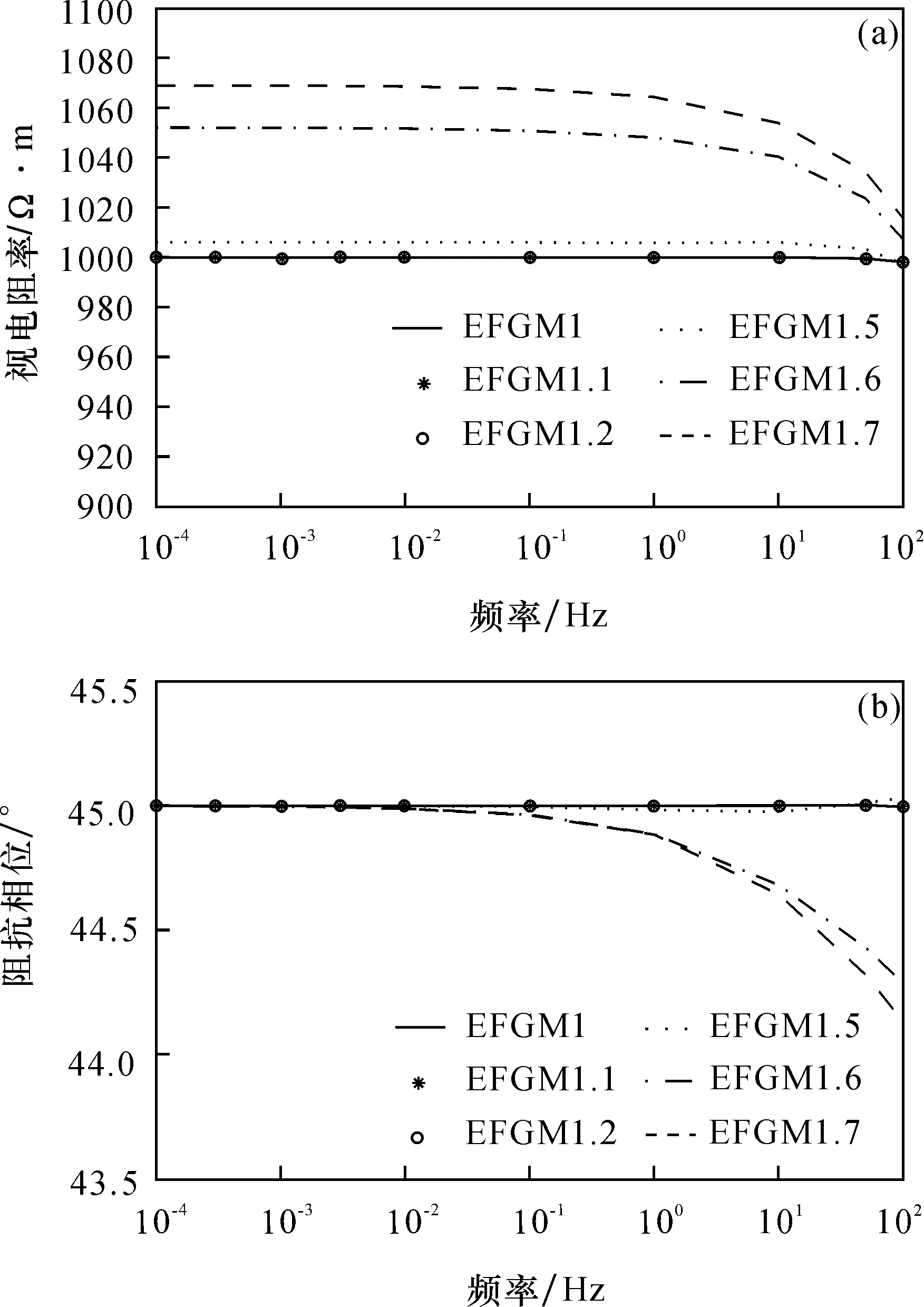
图4 不同支持域无量纲尺寸模型一的EFGM数值计算结果Fig. 4 Calculation results of EFGM for model 1 with different support domain dimensionless sizesa-视电阻率; b-阻抗相位a-apparent resistivity; b-impedance phase

图5 二层介质模型的EFGM数值计算结果Fig. 5 Calculation results of EFGM for two-layer medium modela-阻抗相位;b-视电阻率a-impedance phase;b-apparent resistivity

然而,EFGM模拟三维电磁场响应计算效率较低,模型三采用的剖面方式在64位PC电脑Matlab平台上运行耗时约2h,内存占用约450MB，计算耗时主要来源于形函数构造过程中高斯点支持域内节点的搜索及含背景网格的高斯积分,因此研究高效的积分方法是EFGM三维模拟进入实用的重要手段。

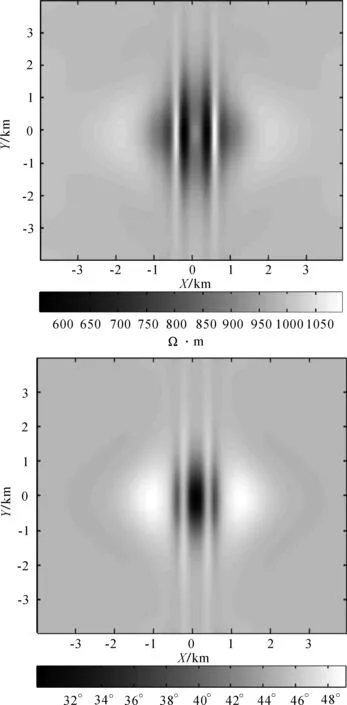
图6 频率为10Hz时模型三EFGM数值计算结果Fig. 6 Calculation results of model 3 by EFGM when frequency is 10Hz

4 结论

本文详述了三维移动最小二乘(MLS)近似原理，推导了MT三维变分问题的无网格离散系统方程，简述了三维背景网格高斯积分与边界条件的罚函数法加载技术。

EFGM求解MT三维变分问题支持域无量纲尺寸最优区间为α=1～1.2,计算精度随α的增大而降低，α的增大同时增加了计算耗时，建议MT正演中取α=1.0。

层状介质模型视电阻率与阻抗相位计算结果均与解析解一致，10Hz频点地表电磁响应特征也较好地反映出了三维异常体的存在，验证了算法的正确性。

Belytschko T, Lu Y Y , Gu L. 1994. Fracture and crack growth by element-free Galerkin methods[J]. Modelling and Simulation in Materials Science and Engineering, 2(3): 519-534

Chen Hui, Deng Ju-zhi, Tan Han-dong. 2011. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 54(6): 1649-1659(in Chinese with English abstract)

Feng De-shan, Wang Hong-hua, Dai Qian-wei. 2013. Forward simulation of Ground Penetrating Radar based on the element-free Galerkin method[J]. Chinese Journal of Geophysics, 56(1): 298-308(in Chinese with English abstract)

Garbon H, Zhdanov M S. 2002. Comtraction intergral equation method in three-dimensional electromagnetic modeling[J]. Radio Science, 37(6): 1089-1101

Jia Xiao-feng , Hu Tian-yue, Wang Run-qiu. 2006 . A mesh-free algorithm of seismic wave simulation in complex medium[J]. Oil Geophysical Prospecting, 41(1): 43-48(in Chinese with English abstract)

Li Dong-ming, Bai Fu-nong, Cheng Yu-min. 2012. A novel complex variable element-free Galerkin method for two-dimensional large deformation problems[J]. Computer Methods in Applied Mechanics and Engineering, 233-236(1): 1-10.

Li Jun-jie, Yan Jia-bin. 2014. Developments of meshless method and applications in geophysics[J]. Progress in Geophysics, 29(1): 452-461(in Chinese with English abstract)

Li Jun-jie, Yan Jia-bin. 2014. Magnetotelluric two-dimensional forward numerical modeling by meshfree point interpolation method[J]. Geophysical Prospecting for Petroleum, 53(5): 617-626(in Chinese with English abstract)

Li Jun-jie, Yan Jia-bin. 2014. Magnetotelluric two-dimensional forward modeling using meshless local Petrov-Galerkin method[J]. Coal Geology & Exploration, 42(6): 101-104(in Chinese with English abstract)

Li Jun-jie, Yan Jia-bin. 2015. A mesh-free method for the variational problem of the point source two-dimensional electric field[J]. Geophysical and Geochemical Exploration, 39(3): 606-609(in Chinese with English abstract)

Li Jun-jie, Yan Jia-bin. 2015. Magnetotelluric two-dimensional forward by finite element-radial point interpolation method[J]. The Chinese Journal of Nonferrous Metals, 25(5): 1314-1324(in Chinese with English abstract)

Liu Chang-sheng, Tang Jing-tian, Ren Zheng-yong. 2010. Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes[J]. Journal of Central South University (Science and Technology), 41(5): 1855-1859(in Chinese with English abstract)

Liu Lei-chao, Dong Xiang-huai, Li Cong-xin. 2009. Adaptive finite element-element-free Galerkin coupling method for bulk metal forming processes[J]. Journal of Zhejiang University-Science A, 10(3): 353-360

Shen Jin-son. 2003. Modeling of 3D electromagnetic responses in frequency domain by using staggered grid finite difference method[J]. Chinese Journal of Geophysics, 46(2): 281-288(in Chinese with English abstract)

Sun Wei-feng, Song Yan, Gong Yan-jie, Gui Li-li. 2014. Characteristics and distribution prediction of structural fissures in the Lower Cretaceous Xiagou Formation in the Qingxi oilfield[J]. Geology and Exploration, 50(6): 1181-1189(in Chinese with English abstract)

Tong Xiao-zhong, Liu Jian-xin, Xie Wei. 2009. Three-dimensional forward modeling for magnetotelluric sounding by finite element method[J]. Journal of Central South University of Technology, 16(1): 136-142

Wittke J, Tezkan B. 2014. Meshfree magnetotelluric modeling[J]. Geophysical Journal International, 198(2): 1255-1268.

Xu Kai-jun, Li Tong-lin, Zhang Hui. 2006. Three-dimensional magnetotelluric forward modeling using integral equation[J]. Northwestern Seismological Journal, 28(2): 104-107(in Chinese with English abstract)

Yan Jia-bin, Li Jun-jie. 2014. Magnetotelluric forward calculation by meshless method[J]. Journal of Central South University (Science and Technology), 45(10): 3513-3520(in Chinese with English abstract)

Yang Li-gong, Liu Ji-shun, Yin Li-jun, Liu Wei-ming, Liu Wen-heng, Guo Jun. 2013. Application of the dual-frequency IP method to rapid prospecting of mineral resources in the Lizi area of Gansu Province[J]. Geology and Exploration, 49(2): 330-336(in Chinese with English abstract)

Zhao Xi-qiang, Li Lin. 2015. Further generalization of Pascal functional matrix and application[J]. Periodical of Ocean University of China, 45(3): 136-140(in Chinese with English abstract)

[附中文参考文献]

陈 辉, 邓居智, 谭捍东. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究[J]. 地球物理学报, 54(6): 1649-1659

冯德山,王洪华,戴前伟. 2013. 基于无单元Galerkin法探地雷达正演模拟[J].地球物理学报, 56(1): 298-308

贾晓峰, 胡天跃, 王润秋. 2006 . 复杂介质中地震波模拟的无单元法[J]. 石油地球物理勘探, 41(1): 43-48

李俊杰, 严家斌. 2014. 无网格法进展及其在地球物理学中的应用[J]. 地球物理学进展, 29(1): 452-461

李俊杰, 严家斌. 2014.无网格点插值法大地电磁二维正演数值模拟[J].石油物探, 53(5): 617-626

李俊杰, 严家斌. 2015. 大地电磁二维正演中的有限元-径向基点插值法[J]. 中国有色金属学报, 25(5): 1314-1324

李俊杰, 严家斌. 2015. 点源二维电场变分问题的无网格解法[J]. 物探与化探, 39(3): 606-609

李俊杰,严家斌. 2014. 无网格局部Petrov-Galerkin法大地电磁二维正演[J]. 煤田地质与勘探， 42(6)：101-104

刘长生, 汤井田, 任政勇. 2010. 基于非结构化网格的三维大地电磁自适应矢量有限元模拟[J]. 中南大学学报(自然科学版), 41(5): 1855-1859

沈金松. 2003. 用交错网格有限差分法计算三维频率域电磁响应[J]. 地球物理学报, 46(2): 281-288

孙维凤, 宋 岩, 公言杰, 桂丽黎. 2014. 青西油田下沟组构造裂缝发育特征与分布预测[J]. 地质与勘探, 50(6): 1181-1189

徐凯军, 李桐林, 张 辉, 2006. 利用积分方程法的大地电磁三维正演[J]. 西北地震学报, 28(2): 104-107

严家斌, 李俊杰. 2014. 无网格法在大地电磁正演计算中的应用[J]. 中南大学学报(自然科学版), 45(10): 3513-3520

杨立功, 刘继顺, 尹利君, 刘卫明, 刘文恒, 郭 军. 2013. 双频激电偶极在甘肃李子地区快速找矿中的应用[J]. 地质与勘探, 49(2): 330-336

赵熙强, 李 琳. 2015. Pascal函数矩阵的进一步推广及应用[J]. 中国海洋大学学报, 45(3): 136-140

Three-Dimensional Forward Modeling of Magnetotellurics Using the Element-Free Galerkin Method

LI Jun-jie1, YAN Jia-bin2, HUANG Xiang-yu2

(1.ZhejiangDesignInstituteofWaterConservancyandHydroelectricPower,Hangzhou,Zhejiang310002; 2.KeyLaboratoryofNon-ferrousResourcesandGeologicalHazardDetection,SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha,Hunan410083)

The element-free Galerkin method (EFGM) is a relatively mature high-precision mesh-free method which avoids the mesh generation and has the advantages in dealing with complex conductivity distribution and geometrical boundaries. This work applies EFGM to three-dimensional forward modeling of magnetotellurism (MT). We introduce the shape function constructing process of three-dimensional EFGM and then deduce the discrete system matrix expression corresponding to the three-dimensional variational problem of MT by combining the Galerkin method and the Gauss integral formula. Then, the approach of assigning boundary conditions is briefly described. Finally, the effect of support domain size on the solution accuracy is studied and the correctness of three-dimensional EFGM is verified by numerical calculations of several models.

mesh-free method, element-free Galerkin method, magnetotelluric, support domain size

2015-01-13；

2015-06-16；[责任编辑]郝情情。

国家自然基金项目(40874055)和湖南省自然基金资助项目(14JJ2012)联合资助。

李俊杰(1989年-)，男，2014年毕业于中南大学，获硕士学位，助理工程师，从事大地电磁无网格化正演研究。E-mail：lijunjiecsu@163.com。

[文献标识码]A [文章编号]0495-5331(2015)05-0946-07