基于贝叶斯压缩感知的正交频分复用信道估计改进
2015-12-07邱尚明李冬睿罗拥华
邱尚明,李冬睿,罗拥华
(广东农工商职业技术学院 计算机系,广东 广州510507)
基于贝叶斯压缩感知的正交频分复用信道估计改进
邱尚明,李冬睿,罗拥华
(广东农工商职业技术学院 计算机系,广东 广州510507)
为了获得理想的正交频分复用信道估计结果,针对传统算法没有充分利用无线信道时域的固有稀疏性,导致估计精度不高且频谱利用率低等难题,提出了改进贝叶斯算法感知的正交频分复用信道估计算法。首先在详细介绍本文算法的原理和步骤基础上,与传统信道估计算法进行仿真对比实验。仿真结果表明,相对于其它信道估计算法,本算法可获得更高的信道估计精度,在使用较少导频的条件下获得很好的信道估计性能。
信道估计;压缩感知;改进贝叶斯;正交频分复用
0 引言
随着无线移动通信技术的发展,对快速移动中的高数据率通信提出了越来越高的要求,正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)采用空时编码,频率占用率低,同时具有抗频率选择性衰落的能力,从而显著提高移动通信系统数据传输率和频谱效,得到了广泛应用[1]。在无线通信系统中,信道估计是OFDM通信系统中最为关键的一环,是进行相干检测、解调和均衡的基础,信道估计的效果直接影响整个通信系统的质量,因此OFDM通信系统的信道估计成为当前研究的重点领域[2]。
针对OFDM系统的信道估计问题,国内外学者进行了大量、深入的研究,取得了一些研究结果,提出许多信道估计方法[3]。信道估计方法分为三类:基于导频估计、半盲估计和盲估计,其中基于导频的估计方法因其低复杂度得到了广泛应用[4]。基于导频的信道估计方法分为频域估计方法和时域估计方法,大量观测数据表明,实际信道在宽带通信的情况下,往往只有少量径的幅度比较大,且多径的数目远小于信道时延扩展内的采样数量,即无线信道在时延域或多普勒-时延域通常会表现出一定的稀疏特性[5,6]。传统的信道估计方法没有充分利用传输信道内在稀疏的这一先验知识,信道估计的准确性和有效性不够高[7]。压缩感知(Compressed Sensing,CS)技术可以从稀疏信号中高效重构原始信号,在包括图像处理、数据压缩和雷达等领域得到广泛应用,为稀疏信道估计提供了一种新的有效途径[8]。文献[9]提出一种基于匹配追踪(Matching Pursuit,MP)算法的稀疏信道估计方法,但是MP算法不是很稳定。文献[10]提出了正交匹配追踪(Orthogonal Matching Pursuit,OMP)的稀疏信道估计算法,然而计算复杂度比较大。
为了提高OFDM的系统质量,针对当前信道估计方法存在的不足,提出一种改进贝叶斯压缩感知的正交频分复用信道估计方法,并通过仿真实验与其他常用信道估计算法性能进行对比。仿真结果表明,本文信道估计方法的频谱利用率以及估计性能更优。
1 OFDM信道模型
若发送端的导频信号为 X=[X1,X2,…,Xm],导频数目为 M,则导频位置接收信号矢量表示为[11]:

式中,ΦM为随机提取矩阵,Z为噪声。
Yp为已知接收信号,则导频位置的信道响应估计为=Yp./X,则有

式中,Z*为服从均值为0,方差为σ2的高斯白噪声,H= Fh为信道响应。代入式(2)得:

2 改进贝叶斯压缩感知的信道估计
稀疏贝叶斯学习方法由贝叶斯学习理论推导而来,信号稀疏表示为


假设稀疏向量h中的每一个元素均服从0均值高斯先验分布,为每个权重系数 hi引入一个超参数 αi,这样稀疏向量h先验分布可表示为:

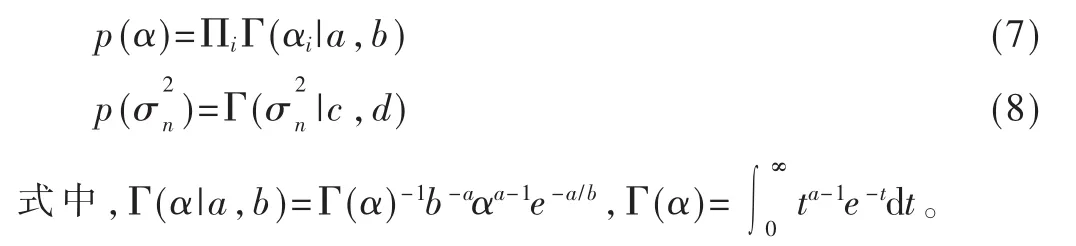
给定h的高斯似然分布,
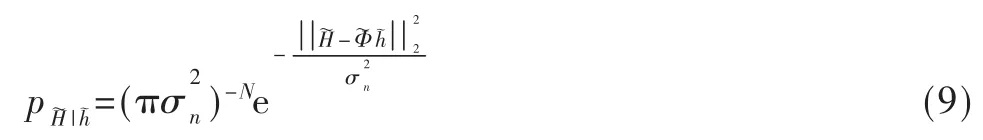
则根据贝叶斯公式,h的后验概率分布函数为

其中,均值和协方差为

式中,A=diag(α1,α2,…,αN),参数 α=(α1,α2,…,αN)T和 α0=要进行估计。
对稀疏信号h的估计问题转化为对参变量α、α0的估计,通常采用最大似然估计。在最大似然法估计超参数过程中,计算复杂度比较大,不利于无线通信系统实时性信道估计。
为了解决该难题,采用改进贝叶斯学习算法对超参数进行估计。具体步骤如下:
(1)选择 α0=合适的初值;
(3)根据式(11)和(12)计算 μ和 Σ,并计算所有的 si和 qi,选择候选的,根据式(13)更新超参数 αi;
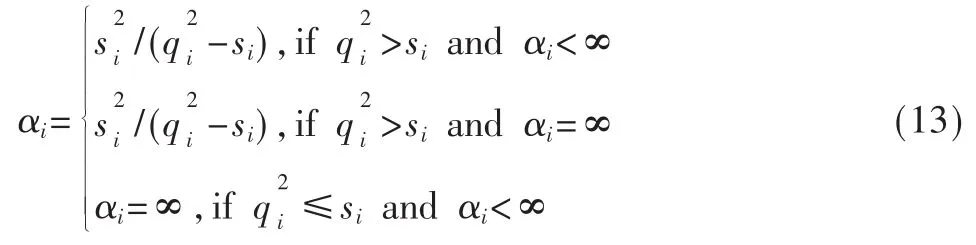
(4)如果收敛,算法结束,h˜=μi;否则,返回步骤(3)继续执行。
3 仿真实验
3.1仿真环境
为了测试本文信道估计方法的性能,在双核CPU 2.85 GHz,内存为4 GB,操作系统为Windows XP计算机上,采用Matlab 2012进行仿真实验。设无线通信系统带宽为20 MHz,多普勒频移为 50 Hz,信道长度 L=256,采用主要路径数为10,即稀疏度K=10,并且假设信道在一个数据符号内是不变的。
3.2对比算法及评价标准
选择LS算法、压缩感知的MP重构算法(MP)和OMP重构算法(OMP)进行对比实验。采用归一化均方误差(Mean Square Error,MSE)和误码率(Bit Error Rate,BER)对信道估计结果优劣进行评价。归一化MSE定义如下
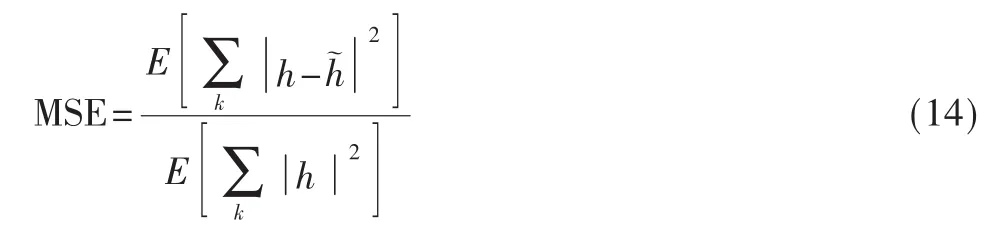
3.3结果与分析
3.3.1信道估计误差比较
信噪比(Signal to Noise Ratio,SNR)为 0~50 dB情况下,LS算法、MP算法、OMP算法和本文算法的归一化均方误差和误码率分别如图1和2所示。对图1和2的结果进行仔细分析,可以得到如下结论:
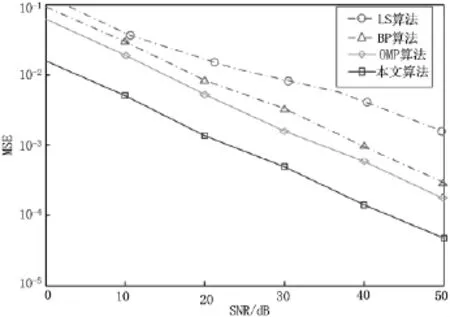
图1 不同算法的MSE与SNR变化关系

图2 不同算法的BER与SNR的变化关系
(1)随着 SNR值不断的增大,所有算法的信道估计误差逐渐减小,即SNR越大,信道估计的精度越高。
(2)在相同的SNR下,对于相同数目的导频符号,MP算法、OMP算法的信道估计性能较LS算法有所提高,主要是由于LS算法没有利用信道的频域和时域的相关特性,并且忽略了噪声的影响,造成信道估计结果对噪声比较敏感,基于压缩感知信道估计算法用更少的导频符号能达到与传统算法相比拟的信道估计性能。
(3)在所有信道估计算法中,本文算法的归一化MSE和BER最小,提高了信道估计精确度和频谱利用率,这主要是由于贝叶斯类算法在进行信道估计时,把噪声考虑进去,并加上合理的噪声分布,导频开销更小,抗噪性更好。
3.3.2信道估计值的误差线范围
信道估计值的误差线范围是衡量信道估计算法的重要标准之一,如果信道估计值的误差线范围比较大,即可以是信道估计误差线范围内的任意值,那么表示信道估计算法的估计结果更加可靠和准确,本文算法的信道估计值的误差线范围如图4所示。从图4可知,本文算法即信道估计值可以是范围内的任意值。而对比算法LS算法、MMSE算法、MP算法、OMP算法只有一个唯一的估计值,无法准确描述信道估计值误差,估计结果更加可信。

图3 信道估计误差
4 结论
针对传统正交频分复用信道估计算法没有充分利用无线信道时域的固有稀疏性,导致估计精度不高且频谱利用率低等难题,压缩感知重构算法和贝叶斯算法,提出一种改进贝叶斯压缩感知的OFDM系统信道估计方法。仿真实验结果表明,相对于传统OFDM系统信道估计方法,本文所提出信道估计算法在较少导频的条件下获得很好的信道估计性能,从而可以提高系统频谱有效性。
[1]LI H,CHIN K H,BERGMANS J W M,et al.Pilot-aided angledomain channel estimation techniques for MIMO-OFDM systems[J].IEEE Transactions on Vehicular Technology,2008,57(2):906-920.
[2]GAO J,LIU H.Low-complexity map channel estimation for mobile MIMO-OFDM systems[J].IEEE Transactions on Wireless Communications,2008,7(3):774-780.
[3]OZDEMIR M K,ARSLAN H.Channel estimation for wireless OFDM systems[J].IEEE Communications Survey&Tutorials. 2007,9(2):14-18.
[4]TUAN H D,KHA H H.Optimized training sequences for spatially correlated MIMO-OFDM[J].IEEE Transactions on Wireless Communications,2010,9(9):2768-2778.
[5]SADOUGH S M S,ICHIR M M,DUHAMEL P,et al. Wavelet-based semi-blind channel estimation for ultra wide and OFDM systems[J].IEEE Trans Veh Technol,2009,58 (3):1302-1314.
[6]BLUMENSATH T,DAVIES M E.Iterative hard threshold for compressed sensing[J].Applied and Computational Harmonic Analysis,2009,27(3):265-274.
[7]BOUZEGZI A,CIBLAT P,JALLON P.New algorithms for blind recognition of OFDM based systems[J].Signal Processing,2010,90(3):900-913.
[8]武林俊.基于叠加训练序列的MIMO-OFDM信道估计[J].电子技术应用,2013,39(3):112-115.
[9]李世平,李鑫,郑文彬.基于压缩感知的正交频分复用信道估计方法[J].电子技术应用,2012,38(8):106-109.
[10]NEEDELL D,VERSHYNIN D.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J].Foundations of Computational Mathematics,2009,9(3):317-334.
[11]TROPP J,GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2012,3(12):4655-4666.
[12]MINN H,BHARGAVA V K,LETAIEF K B.A robust timing and frequency synchronization for OFDM systems[J]. IEEE Transactions on Wireless Communications,2013,2(4):822-839.
OFDM channel estimation algorithm based on improved Bayesian compressive sensing
Qiu Shangming,Li Dongrui,Luo Yonghua
(Department of Computer,Guangdong AIB Polytechnic College,Guangzhou 510507,China)
In order to obtain good channel estimation results of orthogonal frequency division multiplexing,and the traditional channel estimation methods did not make full use of the channel sparsity which leads to low precision estimation and low frequency spectrum utilization,a novel channel estimation algorithm of orthogonal frequency division multiplexing is proposed based on improved Bayesian compressive sensing.Firstly,the principle and steps of the proposed algorithm are introduced in detail,and then the simulation experiments are carried out in order to test the performance of the algorithm.The results show that compared with other channel estimation algorithm,the proposed algorithm can improve the channel estimation precision and has good performance but with less pilots.
channel estimation;compressive sensing;improved Bayesian;orthogonal frequency division multiplexing
TP391.9
A
0258-7998(2015)02-0109-03
10.16157/j.issn.0258-7998.2015.02.026
2014-07-23)
邱尚明(1980-),男,硕士,讲师,主要研究方向:图形图像处理、模式识别、嵌入式控制、地理信息系统。
李冬睿(1983-),男,硕士,讲师,主要研究方向:图形图像处理、模式识别、嵌入式控制。
罗拥华(1978-),男,硕士,讲师,主要研究方向:图形图像处理、模式识别、嵌入式控制、计算机网络应用。
