一种无线传感器网络的盲源分离算法

耿云志，徐慧芳，沈海斌

(1.浙江大学超大规模集成电路设计研究所，浙江杭州310027;2.西湖电子集团有限公司，浙江杭州310012)

0 引言

当前，无线传感器网络在信号传输上依托网络通信协议封装成信息包，信息包中除目标信息外还包含大量的校验纠错码，如奇偶、循环冗余、超时重发等，加重了通信负担，信息包中协议码大于目标码的现象十分常见。盲源分离(blind source separation，BSS)技术不需要任何先验知识就可以直接从接收到的信号中重构出源信号［1］，避开了繁重的纠错校验码，大大减少了通信的带宽负担，成为无线传感器网络领域的研究热点。然而，利用盲源分离技术部署无线传感器网络通常有以下难点:1)传感器、Modem最优个数难以确定;2)量化编码时，难以确定最优量化比特位数;3)部署时难免遇到噪声环境复杂的情况;4)无线传感器网络实时性要求高。因此，对用于无线传感器网络的盲源分离算法要求十分苛刻。

本文主要研究无线传感器网中Modem个数、量化比特位及信噪比(SNR)对平方根容积卡尔曼滤波(SRCKF)分离算法的影响，在传感器网络部署前期，通过SRCKF分离算法可以有效度量出最优量化比特位和Modem个数。最后，在同等最优条件下，将SRCKF算法与基于无先导卡尔曼滤波(UKF)的同类算法进行算法效率度量:SRCKF计算量更少，运行效率更高。

1 无线传感器网络的盲源分离模型

无线传感器网络的拓扑结构有两种［2～4］:一种是节点信号先发到簇头节点，通过簇头节点发给融合中心;另外一种是节点信号直接发到融合中心，如图1所示。

图1 无线传感器网络拓扑结构Fig 1 Topology structure of wireless sensor networks

本文算法基于无簇型传感器网络模型(节点直接发给融合中心)，在融合中心进行盲源分离，进一步得到无簇型无线传感器网络的盲源分离模型，如图2所示。

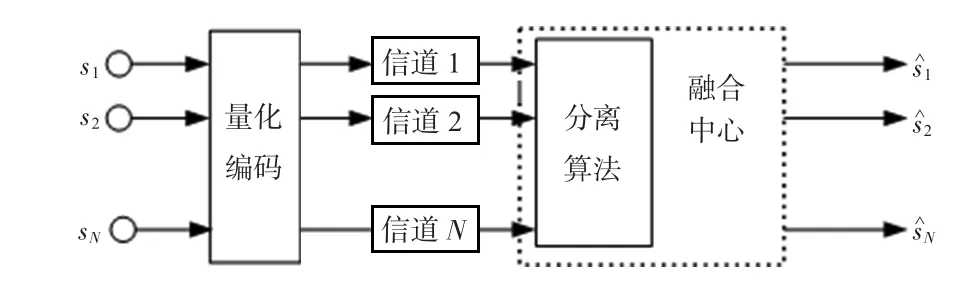
图2 无簇型无线传感器网络的盲源分离模型Fig 2 Blind source separation model for non cluster wireless sensor networks

上述模型中，对融合中心收到的观测信号建立数学模型［5］

式中 sj(k)为第j个源信号，aij为混合矩阵的元素，νi(k)为第i个节点的观测噪声，qi(k)是量化过程引入的量化噪声，N 为传感器网络节点数，i∈1，2，…，M，j∈1，2，…，N。

为顺利对融合中心的接收信号盲源分离，对无线传感器网络作如下假设:

1)融合中心的能量和通信带宽没有限制。

2)信道之间无冲突和信号衰减。

3)传感器的节点个数N不大于Modem个数M，即N≤M。

2 盲源分离算法

将方程(1)改写成对应的矩阵向量形式

式中 A为元素aij组成的M×N混合矩阵，s为元素sj(k)组成的源信号向量，u为νi(k)-qi(k)元素组成的混叠噪声向量。

盲源分离的本质在于求解源信号对应的解混矩阵W，用观测向量和混合信号的乘积实现源信号的提取

利用概率论知识，当迭代产生的W，满足‖s-^s‖≤ε，ε是一个非常小的正数，表示分离矩阵W求解完成。

分离出来的信号^s是源信号s的估计，满足信号的迭代方程

根据主成分分析原理，定义目标函数如下

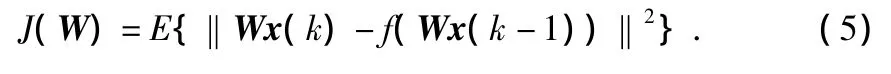
由于混合矩阵A是常量矩阵［6］，所以，分离向量W是线性时不变的，根据这一特性得到状态空间方程

将式(3)代入式(5)中，且根据表达式(6)的关系，得分离测量方程如下

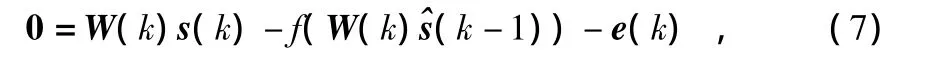
式中 e(k)为误差向量，k为采样节点数。

根据状态空间方程(6)和分离测量方程(7)，利用SRCKF［7］，可以设计盲源分离算法如下:

1)参数初始化

式中 E［·］为求数学期望，sprt{.}为求平方根操作，wj，0为初始状态向量，其协方差矩阵的平方根矩阵为sj，0。

2)计算求容积分点、估计预测值并更新误差协方差矩阵的平方根矩阵

其中，Qk为状态转移误差的协方差，sQ，k为Qk的平方根矩阵，qr{·}为矩阵的QR分解。χik|k-1是一个nw×2nw维的带权值和去均值矩阵，sk|k-1为方差的平方根，维度是nw×nw。

3)计算卡尔曼增益、更新状态矩阵

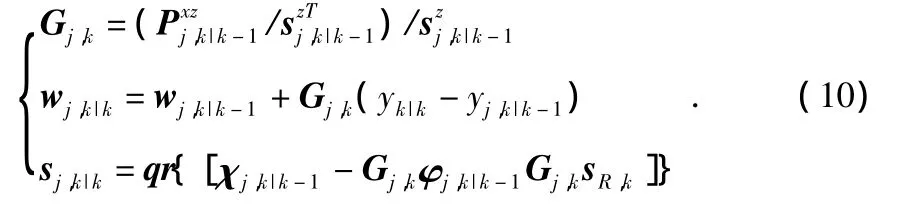
3 仿真与分析

混沌信号具有非周期、有界、不收敛、类随机的特点，广泛用于无线传感器网络的信号调制研究中，实验选取两个节点，分别由 Logistic 映射［8］和 Chebyshev 映射［9］产生，表达式如下

式中 s1(k)≤1，s2(k)≤1，α，β 是混沌参数，当 α≤2，β≥2时系统处于混沌状态，本文采用源信号和分离信号的均方误差评估算法性能，均方误差(MSE)值为 MSES1(k)，MSES2(k)的均值，MSE数学定义

图3显示了SRCKF算法中，量化比特数、Modem个数对MSE的影响，MSE以增益形式显示。仿真结果:其它条件最优时，MSE随Modem数、量化比特位数的增加而改善，量化比特位M=4时，MSE=0.012(增益 -38.41dB);当Modem个数N=2(满足节点数不大于Modem数)，MSE=0.0025(增益 -52 dB)。

图3表明:过多的Modem数和量化比特位对SRCKF算法的分离效果并没有帮助，且量化比特位数的增加会增加无线通信的负担。在传感器网络部署前期，可借助SRCKF算法通过MSE指标的预估值，反向求解最佳Modem数和量化比特位数，减小不必要的Modem损失和无线传输负担。

图3 MSE与Modem数、量化比特的关系Fig 3 Relationship between MSE and number of Modem and quantization bits

图3确定了最佳量化比特数和Modem数后，下面的实验里，令最优Modem数N=2，最优量化比特位数M=4，在此条件下讨论MSE与SNR的关系如图4所示。

图4 MSE与SNR的关系Fig 4 Relationship between MSE and SNR

图4仿真结果显示:MSE指标随着SNR的增加有所改善，但当SNR增加到一定程度(本实验为35 dB)时，MSE指标的优化效果就不明显了，后面的效率度量实验中令SNR=35 dB。

文献［10］提出了一种UKF的盲源分离算法，与本文SRCKF算法属于同类别，图5是对SRCKF和UKF算法在同一条件下的运行时间对比度量。混沌参数α=2，β=2，节点数N=2，量化比特M=4，SNR=35 dB，混合矩阵A随机产生，进行100次分离实验。UKF算法运行一次平均需要0.7904ms，SRCKF算法运行一次平均需要0.5821ms，占UKF算法运行时间的的73.646%，运算效率是UKF算法的1.3578倍。

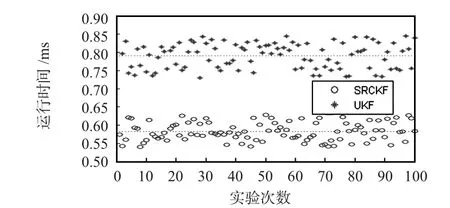
图5 基于SRCKF盲源分离算法效率Fig 5 Efficiency of blind source separation algorithm based on SRCKF

4 结论

本文针对无线传感器网络的问题，提出一种SRCKF盲源分离算法，算法利用解混矩阵W的时不变性生成状态空间方程，并采用主分量分析法生成分离测量方程。

实验表明:在无线传感器网络部署前期，可借助SRCKF分离算法反向求解最佳Modem数和量化比特位数，减小不必要的Modem损失和无线传输负担。在同等最优Modem数和量化比特位下，SRCKF算法相比于同类UKF算法效率更高。

［1］Lee T W.Independent component analysis［M］.New York:Springer，1998.

［2］Banani SA，Vaughan R G.Blind channel estimation for equalisation in dispersive fading channel［J］.IET Communications，2011，5(11):1577-1586.

［3］于海斌，梁 炜，曾 鹏.智能无线传感器网络系统［M］.北京:科学出版社，2013.

［4］Li Y，Amari SI，Cichocki A，et al.Underdetermined blind source separation based on sparse representation［J］.IEEE Transactions on Signal Processing，2006，54(2):423-437.

［5］Belouchrani A，Abed-Meraim K，Cardoso J F，et al.A blind source separation technique using second-order statistics［J］.IEEE Transactions on Signal Processing，1997，45(2):434-444.

［6］Hyvärinen A，Karhunen J，Oja E.Independent component analysis［M］.Hoboken:John Wiley ＆ Sons，2004.

［7］黄锦旺.传感器网络中的信号分离与重构［D］.广州:华南理工大学，2014.

［8］凌 聪，孙松庚.Logistic映射扩频序列的相关分布［J］.电子学报，1999，27(1):140-141.

［9］雷利华，马冠一，蔡晓静，等.基于 Chebyshev映射的混沌序列研究［J］.计算机工程，2009，35(24):4-6.

［10］盛 堰，周 飞，李鉴鸿，等.一种水下无线传感器网络数据的盲分离算法［J］.传感器与微系统，2013，32(10):106-109.