不确定采样系统的鲁棒镇定控制器设计

王 炜，周维龙

（1. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2. 湖南铁道职业技术学院，湖南 株洲 412001）

不确定采样系统的鲁棒镇定控制器设计

王 炜1,2，周维龙1

（1. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2. 湖南铁道职业技术学院，湖南 株洲 412001）

讨论不确定采样控制系统的鲁棒稳定和镇定问题。通过将采样控制系统变换为具有分段连续时滞的线性模型，基于Lyapunov-Krasovskii泛函方法，获得了系统的鲁棒稳定性条件，给出了状态反馈镇定控制器的设计方法。最后，数值例子表明了本方法的有效性；且相比于文献[6]中所提方法得到的结果，本方法更优越。

采样控制系统；Lyapunov-Krasovskii泛函；稳定和镇定

0 引言

采样是数字控制系统中不可缺少的环节，因此采样控制系统受到了广大学者的关注[1-2]。文献[3]利用提升技术方法将原系统等价地变换为有限维离散系统，然后应用离散系统的方法设计镇定控制器，但当采样时间和系统矩阵参数具有不确定性时，该方法将不再适用。文献[4]利用混合离散/连续模型方法给出了保证系统稳定的充要条件，这个充要条件是求解一组具有跳跃的微分不等式，但是求解微分不等式组较困难。文献[5]通过引入分段连续Lyapunov函数，在等时间间隔采样条件下，得到基于矩阵不等式的稳定条件，给出了基于迭代算法的控制器设计方法，然而，对于充分小的采样周期，这些不等式近乎无解。文献[6]将输入控制信号表示为具有分段连续时变时滞的控制模型，然后利用Lyapunov-Krasovskii泛函方法获得基于线性矩阵不等式的稳定性条件，然而，这些条件没有考虑时滞导数信息，导致结果具有较大的保守性。

因此，本文讨论不确定采样系统的鲁棒镇定控制器设计问题。首先，将控制输入表示为具有时变分段连续时滞的连续时间控制模型，然后构造新的Lyapunov-Krasovskii泛函，充分利用时滞导数信息，获得了基于LMI的稳定性条件，并给出了相应的控制器设计算法。最后，通过一个数值实例来验证所提方法的有效性。

1 问题描述

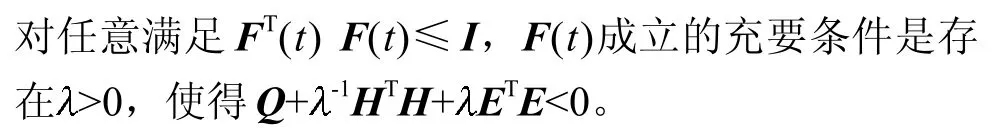
2 主要结果

本文首先应用引理1建立闭环系统（5）的渐近稳定条件，然后给出控制器的设计方法，最后将结论推广到具有时变参数不确定性的系统。

3 数值例子

下面本文通过一个数值例子来说明本方法的有效性。

例1 考虑系统（1）具有如下参数：

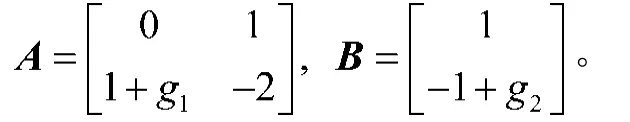
式中：|g1|≤0.1；|g2|≤0.3。

首先，将系统矩阵A, B分别表示为：

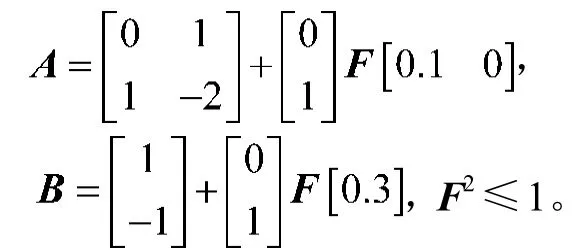
文献[6]给出的保证系统鲁棒稳定的最大采样时间间隔为h=0.805，相应的控制器增益矩阵K=[-1.714 6 -0.426 3]。而采用本文定理4，取 =0.12时，求解式（13）和式（20），得到的最大采样时间间隔为h=0.822，相应的控制器增益矩阵K=[-1.724 4 -0.415 7]。显然，本方法得到的结果具有更小的保守性。

4 结语

本文讨论了采样控制系统的镇定问题。基于Lyapunov-Krasovskii泛函方法，获得了保证系统稳定的充分判据，并给出了镇定控制器的设计方法。数值例子表明了所提方法的可行性，与文献[6]所提方法相比，更具优越性。

[1] Banieh B，Pearson J B，Francis B A，et al. A Lifting Technique for Linear Period Systems with Applications to Sampled-Data Control[J]. Systems & Control Letters，1991，17(2)：79-88.

[2] Dullerud G，Glover K. Robust Stabilization of Sampled-Data Systems to Structured LMI Perturbations[J]. IEEE Transactions on Automatica Control，1993，38：1497-1508.

[3] Oishi Y. A Bound of Conservativeness in Sampled-Data Robust Stabilization and Its Dependence on Sampling Periods[J]. Systems & Control Letters，1997，32(1)：11-19.

[4] Sivashankar N，Khargonekar P. Characterization of the L2-Induced Norm for Linear Systems with Jumps with Applications to Sampled-Data Systems[J]. SIAM Journal of Control and Optimization，1994，32：1128-1150.

[5] Hu L，Cao Y，Shao H. Contrained Robust Sampled-Data Control for Nonlinear Uncertain Systems[J]. International Journal of Robust and Nonlinear Control，2002，12：447-464.

[6] 王 炜，曾红兵. 不确定线性采样系统鲁棒稳定性[J].湖南工业大学学报，2010，24(4)：79-81. Wang Wei，Zeng Hongbing. Robust Stability of Uncertain Linear Sampling Systems[J]. Journal of Hunan University of Technology，2010，24(4)：79-81.

[7] Park P，Ko J W，Jeong C. Reciprocally Convex Approach to Stability of Systems with Time-Varying Delays[J]. Automatica，2011，47(1)：235-238.

[8] Petersen I R，Hollot C V. A Riccati Equation Approach to the Stabilization of Uncertain Linear Systems[J]. Automatica，1986，22(4)：397-411.

[9] Boyd S，El Ghaoui L，Feron E，et al. Linear Matrix Inequality in Systems and Control Theory[M]. Philadelphia：Society for Industrial and Applied Mathematics，1994：56-60.

[10]于显利. 线性不确定系统鲁捧耗散控制研究[D]. 大庆：东北石油大学，2006. Yu Xianli. Robust Dissipation Control for Uncertain Linear Systems[D]. Daqing：Northeast Petroleum University，2006.

[11]刘善伍. 不确定采样系统鲁棒稳定性分析与鲁棒控制[D].哈尔滨：哈尔滨理工大学，2006. Liu Shanwu. Robust Stability Analysis and Robust Control of Uncertain Sampled-Data Systems[D]. Harbin：Harbin University of Science and Technology，2006.

[12]廖晓昕. 漫谈Lyapunov稳定性的理论、方法和应用[J]. 南京信息工程大学学报：自然科学版，2009，1(1)：1-15. Liao Xiaoxin. Talking on the Theory, Methods and Application of Lyapunov Stability[J]. Journal of Nanjing University of Information Science & Technology：Natural Science Edition，2009，1(1)：1-15.

[13]高 莲，包曙红. 关于Lyapunov稳定性若干定理的推广[J]. 内蒙古师范大学学报：自然科学汉文版，2006，35(4)：407-412. Gao Lian，Bao Shuhong. The Generalization of Theorems About Lyapunov Stability Theory[J]. Journal of Inner Mongolia Normal University：Natural Science Edition，2006，35(4)：407-412.

（责任编辑：邓 彬）

Design of Robust Stabilization Controller for Uncertain Sampled-Data Systems

Wang Wei1,2，Zhou Weilong1
（1. School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. Hunan Railway Professional Technology College，Zhuzhou Hunan 412001，China）

Discusses the robust stabilization of uncertain sampled-data control system. By transforming sampleddata control system into a linear model of segment continuous time delay and based on Lyapunov-Krasovskii functional method, obtains the system robust stabilization conditions and presents the design method of state feedback stabilization controller. The numerical instance demonstrates the effectiveness of the proposed method, and comparing to the result from Reference [6], the method is super.

sampled-data system；Lyapunov-Krasovskii functional；stability and stabilization

TP13

A

1673-9833(2015)02-0050-04

10.3969/j.issn.1673-9833.2015.02.009

2015-01-12

国家自然科学基金资助项目（61304064），湖南省自然科学基金资助项目（2015JJ3064）

王 炜（1979-），女， 天津人，湖南铁道职业技术学院高级讲师，主要研究方向为电气自动化，E-mail：wangwei9804@163.com