单调荷载下开洞短肢剪力墙力学性能的有限元分析

刘 星，杨晓华，陈端云，鲁 楠

（湖南工业大学 土木工程学院，湖南 株洲 412007）

单调荷载下开洞短肢剪力墙力学性能的有限元分析

刘 星，杨晓华，陈端云，鲁 楠

（湖南工业大学 土木工程学院，湖南 株洲 412007）

为了研究开洞口对L形截面短肢剪力墙力学性能的影响，在短肢剪力墙的截面尺寸和配筋率保持不变的情况下，运用ANSYS有限元软件，对不同开洞率的短肢剪力墙的力学性能进行研究，分析短肢剪力墙的承载力和屈服位移。模拟结果表明，短肢剪力墙的承载能力随着短肢剪力墙开洞率的增加而降低，短肢剪力墙腹板底部以及开洞处是试件最薄弱的部位，开洞会降低短肢剪力墙的单调荷载下的力学性能，短肢剪力墙开洞直径不宜过大。

短肢剪力墙；开洞率；力学性能

0 引言

短肢剪力墙结构是在融合了框架结构和剪力墙结构的双重优点的基础上发展起来的一种新型的建筑结构形式。与普通剪力墙相比，短肢剪力墙更合理，抗侧力更大，从而使短肢剪力墙结构在实际工程尤其是在多高层建筑中得到了广泛应用。

短肢剪力墙在实际工程中有良好的建筑功能，国内外有学者对短肢剪力墙结构体系进行了较多的实验和理论研究。容柏生最先提出短肢剪力墙结构体系，并将这一结构体系运用到我国实际工程中[1]。根据相关文献[2]的规定，如果在短肢剪力墙上进行开洞处理，开洞面积一般小于整个剪力墙墙面面积的15%，而且相邻洞口间距以及洞口至墙边的距离大于孔洞长边尺寸时，可以忽略孔洞的影响。当孔洞的面积相对较大时，必须考虑孔洞的位置、大小对短肢剪力墙抗震性能的影响[3]。一般情况下，如果剪力墙开洞面积超过规范所规定的要求，且洞口的位置或形状不规范时，通常都是通过运用ANSYS等有限元分析软件进行分析[4]。王激扬等[5]通过4个不同剪力墙试件的拟静力试验后认为，不同的开洞位置使剪力墙极限承载力在不同受力方向上存在一定差异，在开洞位置相同的情况下，剪力墙承载力和抗侧刚度的大小随开洞率（洞口面积与剪力墙墙面面积的比值）的增大而减小。付善春等[6]在他人研究的基础上进一步研究了不同开洞率、孔洞位置对剪力墙刚度及侧向位移的影响，分析得出在开洞位置相同的情况下，开洞率的加大使得剪力墙的刚度大幅下降，侧向位移大幅增加。

本文在开洞位置保持不变的情况下，以不同开洞率的剪力墙为研究对象，运用ANSYS有限元分析软件计算得出等效侧移刚度，以及在相同轴压比下水平均布荷载作用在剪力墙定点的位移。通过比较分析找出开洞对短肢剪力墙力学性能影响的规律。

1 非线性有限元分析

1.1 钢筋混凝土有限元模型

通过ANSYS有限元分析软件建立模型有3种方式，即分离式模型、整体式模型、组合式模型。本文选用分离式模型来建立混凝土有限元模型。分离式模型是把混凝土与钢筋用2种不同的单元来进行处理，混凝土主要采用Solid单元；钢筋是一种细长的材料，通常不考虑其横向抗剪强度，可以将它作为线单元处理，主要采用Link单元。一般情况下，由于各种环境因素的影响，钢筋混凝土会开裂，导致钢筋和混凝土之间协调性降低，产生粘结失效和滑移。相对于整体式模型，分离式模型的应用较广泛。

1.2 剪力墙的尺寸

模型的实际结构为L型开洞短肢剪力墙现浇混凝土结构，为计算方便，建立了1/2缩尺比例的有限元计算模型，试件的相似关系如表1所示。

表1 剪力墙的相似关系Table 1 Similar relationship for shear walls

剪力墙尺寸为1500 mm×700mm，厚度为100 mm；剪力墙配筋采用双层双向配筋，纵筋为126，箍筋为4@200；钢筋保护层厚度为20 mm；混凝土强度等级采用C30。剪力墙截面配筋如图1所示。

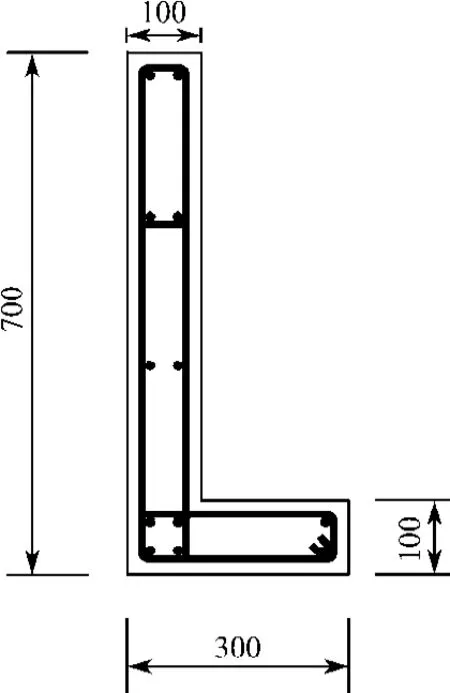
图1 剪力墙配筋图Fig.1 Shear wall reinforcement diagram

在L型短肢剪力墙结构有限元计算模型中，现浇混凝土部分采用Solid 65[7]单元进行划分，钢筋部分选用Link 8[8]单元进行划分。分析中假定钢筋与混凝土之间不存在缝隙，不会产生相对滑移。

本文设计6个L型开洞短肢剪力墙，剪力墙的各参数如表2所示。

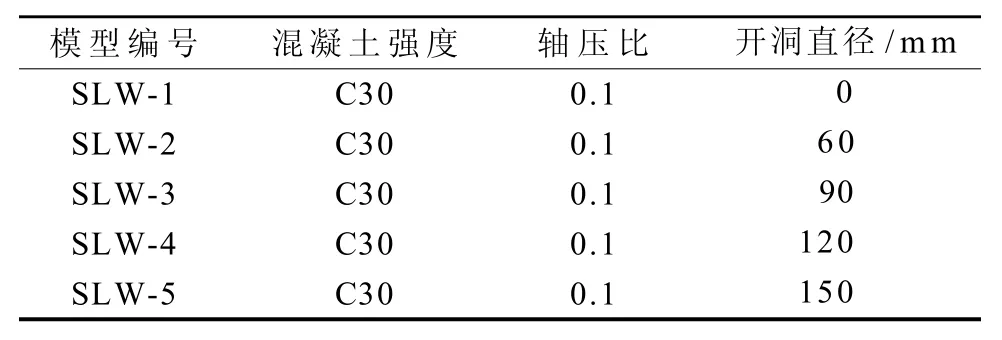
表2 剪力墙参数Table 2 Parameters of the shear walls

1.3 材料参数

在Solid 65单元中，混凝土材料破坏准则选用WW五参数破坏准则，用于判定混凝土材料的开裂和压碎状态；混凝土材料选用多线性随动强化模型。混凝土单轴应力-应变关系，上升段根据相关规范[9]规定的公式求出，下降段则采用Hongnestad的处理方法求出，并有如下公式：

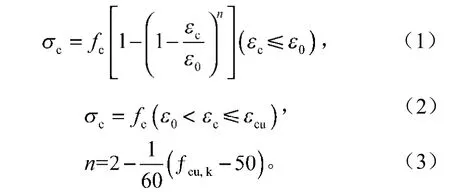
fc为混凝土轴心抗压强度；

n为系数，当其计算值大于2.0时，取值2.0；

fcu,k为混凝土立方抗压强度标准值。

混凝土的应力-应变关系如图2所示。

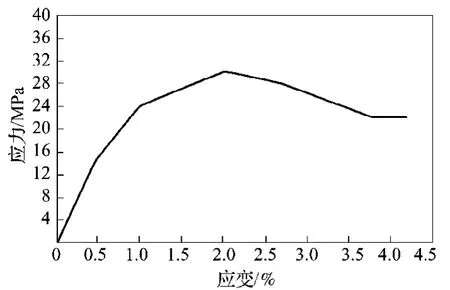
图2 混凝土的应力-应变曲线Fig.2 The stress-strain curve of concrete

钢筋采用HRB335屈服强度标准335 MPa。在ANSYS有限元分析中，一般情况下钢筋看作理想弹塑性材料，钢筋的本构关系选用典型的双线性模型，用斜直线来代替塑性阶段及强化阶段，斜直线斜率为弹性模量的1%，以此模拟钢材的弹塑性阶段双线性随动强化模型。屈服准则遵守Von Mises屈服准则及相应流动法则。其应力应变关系为线性关系，并有如下公式：

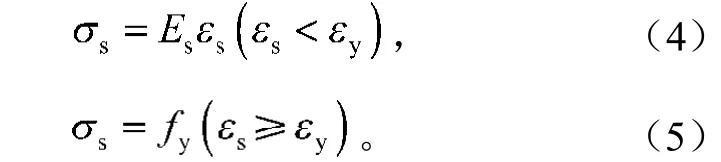
fy为材料的屈服强度。

钢筋的应力-应变关系如图3所示。

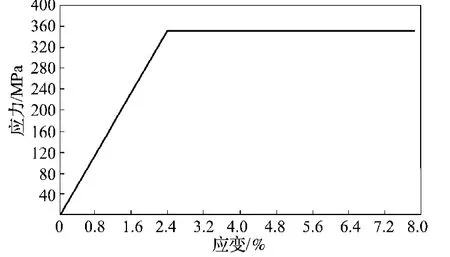
图3 钢筋的应力-应变曲线Fig.3 The stress-strain curve of steel bar

1.4 模型边界条件和加载

在有限元分析中，假定剪力墙的底部（图4中的A面）固定不动，即在剪力墙底部限制其6个方向上的自由度，剪力墙的顶部可以自由移动。在剪力墙顶部（图4中的C面）按照设计轴压比（轴压比为0.1），一次性均匀施加竖向荷载N，而后在剪力墙顶部（图4中的B面）x方向施加一个正向的水平荷载。其中竖向荷载的计算公式为

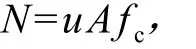
式中：u为轴压比，非抗震地区，u=0.9；

A为截面面积；

fc为混凝土抗压强度设计值。

模型边界条件及网格的划分如图4～5所示。

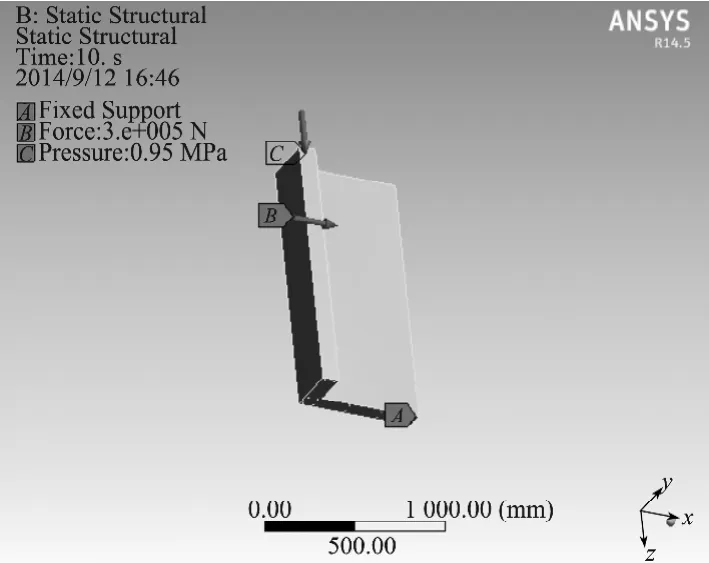
图4 边界条件示意图Fig.4 Schematics of the boundary condition

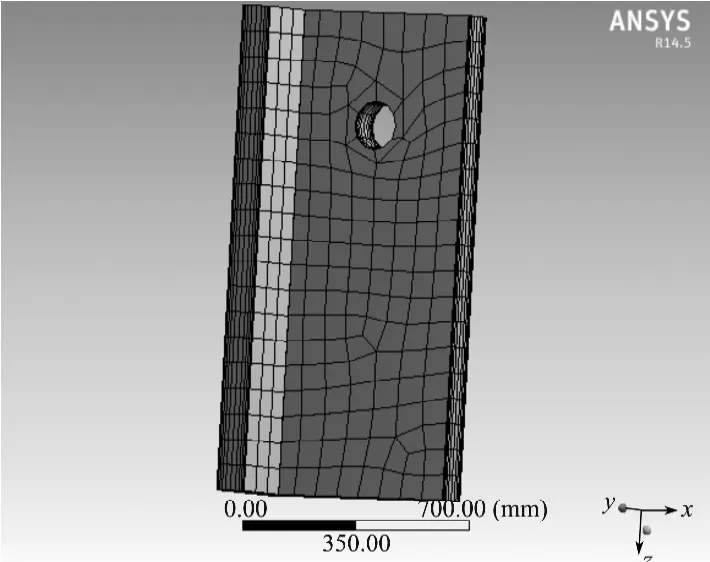
图5 网格划分示意图Fig.5 Schematics of the mesh

2 试验结果及分析

有限元计算模型建立后，分别对SLW-1， SLW-2， SLW-3， SLW-4， SLW-5 五块剪力墙试件的有限元计算模型顶部 轴正向施加均布荷载，荷载达到一定数值后保持不变。当试件稳定后，在剪力墙顶部x轴正向施加均布荷载，荷载采用单调加载方式，按事先设计好的荷载步不断增加剪力墙面均布荷载直至剪力墙破坏。5块剪力墙计算模型的每级荷载步荷载的增量完全相同，每级荷载增量为10 kN。有限元分析模型应力计算结果采用云图方式表达，它能清晰地反映剪力墙在全过程应力分布的变化情况。

2.1 未开洞短肢剪力墙的破坏过程

根据试件在某一时刻荷载所得到的位移，未开洞的短肢剪力墙（SLW-1）的荷载-位移曲线图如图6所示。

图6 SLW-1 荷载-位移曲线Fig.6 Load-displacement curve of SLW-1

由图6可知，未开洞的短肢剪力墙在54.32 kN时达到屈服，此时受压侧混凝土底部还未达到其抗压强度，而受拉侧的混凝土角部刚刚达到其抗拉强度，钢筋受拉侧纵筋和受压侧纵筋都有部分屈服，在达到屈服点之前的荷载位移曲线近似于直线。继续施加荷载，剪力墙位移变化急剧增大，当加至极限荷载107.43 kN时，剪力墙发生破坏，受拉侧的混凝土破坏面增大，受压侧混凝土角部开始破坏，受拉侧纵筋屈服区域明显扩大，从屈服点到极限荷载阶段，剪力墙所表现出来的荷载-位移曲线是一段弧线。继续施加荷载，混凝土破坏面积进一步增大，纵筋受拉侧的屈服区域进一步扩大。

试件在整个过程中的应力云图如图7所示。

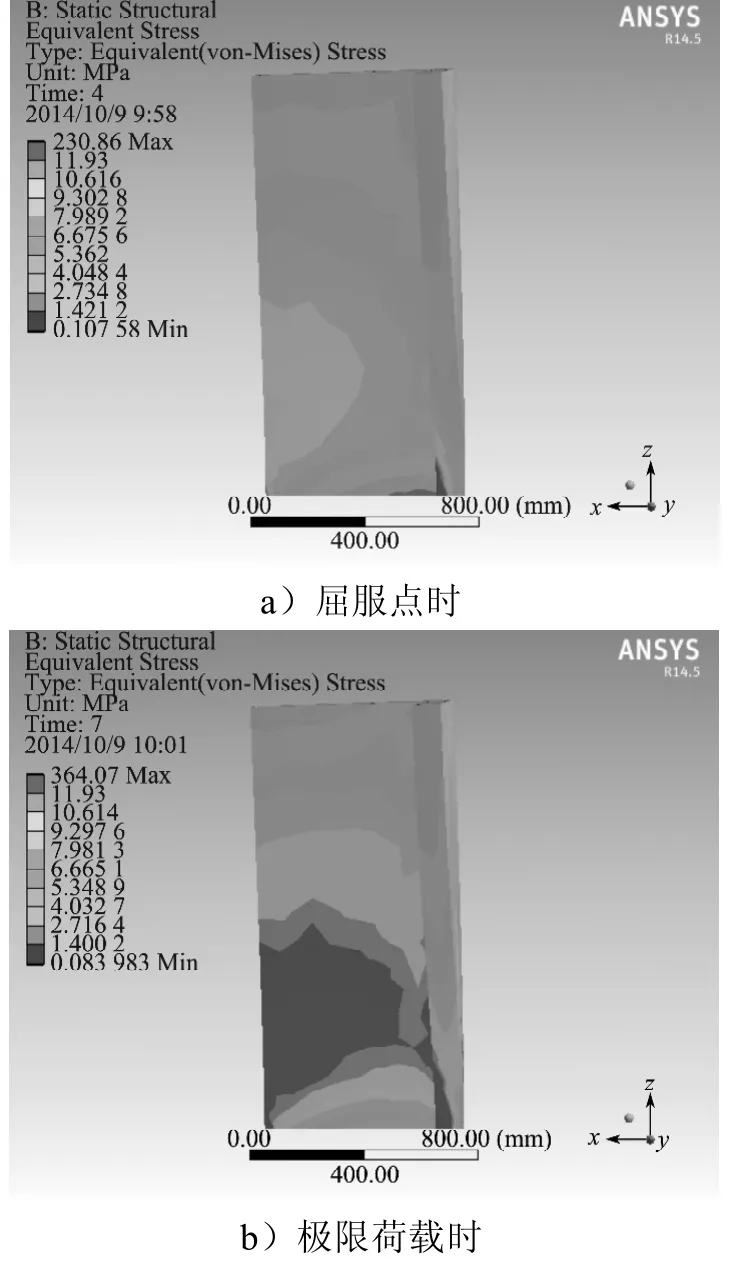
图7 剪力墙SLW-1受力过程应力图Fig.7 The stress nephogram of SLW-1

从受力角度来看，此剪力墙是典型的压弯构件，且此剪力墙属于高剪力墙。由于剪力墙底部的弯矩比较集中，所以剪力墙底部的应力最大，剪力墙破坏先从底部开始，呈弯曲破坏。

2.2 开洞对短肢剪力墙力学性能的影响

根据我国现行的规范[2]中规定，在剪力墙墙体上开洞的位置和大小会从根本上影响剪力墙的受力状态和变形特点。为了研究开洞大小对剪力墙力学性能的影响，本文设计4块开洞位置不变，开洞直径分别为60, 90, 120, 150 mm的剪力墙（SLW-2, SLW-3, SLW-4, SLW-5），并与1块未开洞的剪力墙（SLW-1）作对比试验。开洞短肢剪力墙混凝土达到屈服点时，孔洞点附近的应力云图如图8所示；剪力墙屈服后到达极限荷载发生弯曲破坏时的应力云图如图9所示。

由图8可知，不同开洞直径的剪力墙在达到屈服点的应力云图相差不大。其都是剪力墙底部的应力最大，此时受压一侧的混凝土底部还未达到其抗压强度，而受拉侧的混凝土角部刚刚达到其抗拉强度，钢筋受拉侧纵筋和受压侧纵筋都有部分屈服，在孔洞处还没有产生较大的应力集中。

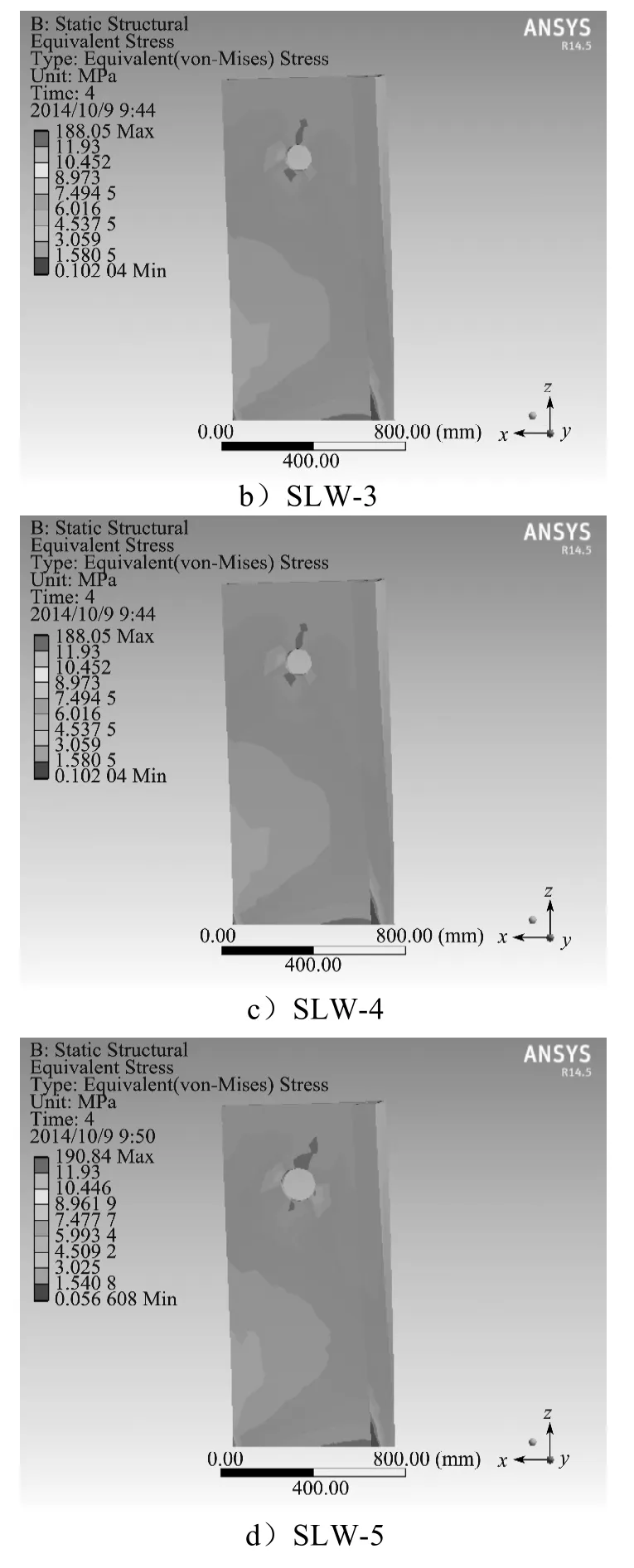
图8 剪力墙屈服时的应力云图Fig.8 The stress nephogram of shear wall yield

由图9可知，在达到极限荷载时，在剪力墙SLW-5孔洞处已经产生较大的应力；随着荷载继续增加，各剪力墙底部破坏面积增大，孔洞处的应力持续增加；当荷载增至94.82 kN时，SLW-5已经完全破坏。

剪力墙SLW-5完全破坏时的应力云图如图10所示，SLW-5完全破坏时其它剪力墙的应力云图如图11所示。

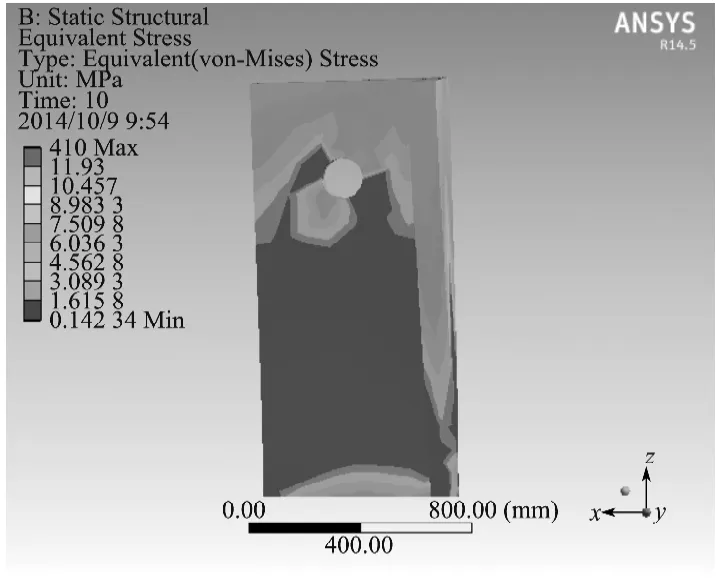
图10 SLW-5破坏时的应力云图Fig.10 The stress nephogram of SLW-5 damage

图11 SLW-5完全破坏时其它剪力墙的应力云图Fig.11 The stress nephogram of other shear walls when SLW-5 damaged

2.3 不同试件力学性能对比分析

5块试件的荷载-挠度曲线如图12所示，其力学性能指标如表3所示。

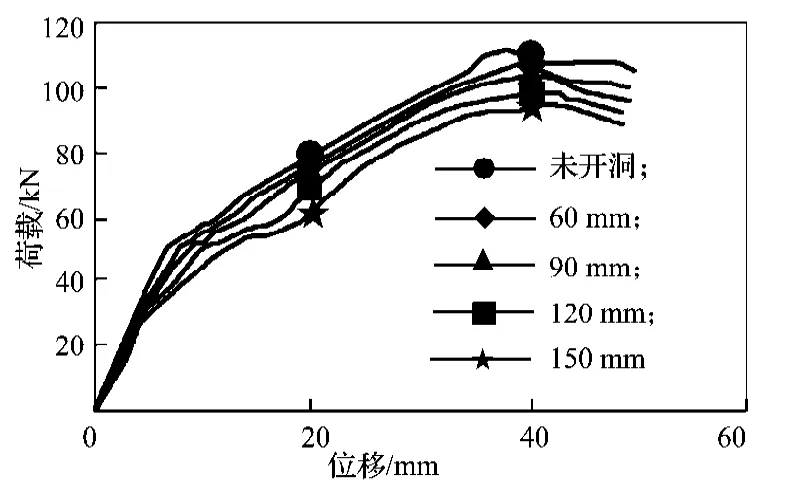
图12 荷载-挠度曲线Fig.12 The load - deflection curve

从5块不同剪力墙试件在屈服点、极限荷载、以及SLW-5完全破坏时的应力云图可以看出，当5块剪力墙未达到屈服点时，底部的应力均最大，在孔洞处还未产生较大的应力。随着荷载继续增加，孔洞处的应力急剧增大，且开洞直径越大，应力越大，剪力墙底部也开始破坏，破坏从底部逐步向顶部发展。继续施加荷载，当荷载增至94.82 kN时，SLW-5最先完全破坏，其他剪力墙也都发生不同程度的破坏，直至荷载施加到107.43 kN时，未开洞的剪力墙才完全破坏。随着开洞直径的增大，剪力墙的承载性能相对减弱。

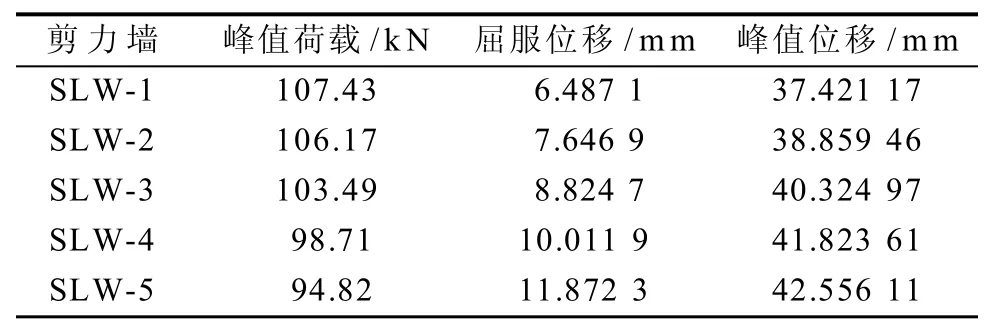
表3 力学性能指标Table 3 The mechanical property index

由荷载-挠度曲线（图12）和力学性能指标（表3）可以看出，开孔洞降低了剪力墙抗弯曲刚度和破坏时的延性，这对结构非常不利。同时，开孔洞使孔洞处的钢筋屈服速度加快，由此降低了剪力墙的极限荷载，随着开洞直径的增加，剪力墙的极限荷载随之降低。

3 结语

运用ANSYS进行钢筋混凝土的有限元分析时，采用分离式模型可较好地模拟混凝土和钢筋的力学性能，同时也能较好地模拟剪力墙孔洞处的破坏形态，计算结果收敛性也较好。

通过比较不同开洞直径的短肢剪力墙模拟结果可知，在剪力墙上开洞降低了墙体的刚度，墙体承载性能降低。如果必须要在剪力墙上开洞，不宜开大洞。

[1] 容柏生. 高层住宅建筑中的短肢剪力墙结构体系[J]. 建筑结构学报，1997，18(6)：14-19. Rong Baisheng. Short-Leg Shear Wall Structural System Used in Tall Residential Buildings[J]. Journal of Building Structures，1997，18(6)：14-19.

[2] 中华人民共和国住房和城乡建设部. JGJ3—2010高层建筑混凝土结构技术规程[S]. 北京：中国建筑工业出版社，2010：79.Ministry of Housing and Urban-Rural Development of the People's Republic of China. JGJ3—2010 Technical Specification for Concrete Structures of Tall Buildings[S]. Beijing：China Architecture & Building Press，2010：79.

[3] Taylor C P，Cote P A，Wallanee J W. Design of Slender Reinforced Concrete Walls with Openings[J]. ACI Structural Journal，1998，95(4)：420-433.

[4] 汪梦甫，周锡元，黄立忠.钢筋混凝土开洞剪力墙结构抗震非线性有限元分析[J]. 地震工程与工程振动，2005，25(3)：47-54. Wang Mengfu，Zhou Xiyuan，Huang Lizhong. Nonlinear Seismic Response Analysis Method of Reinforced Concrete Shear Walls with Opening[J]. Earthquake Engineering and Engineering Vibration，2005，25(3)：47-54.

[5] 王激扬，楼文娟，田中仁史.开洞形式对混凝土剪力墙抗震性能的影响[J].建筑结构学报，2009，30(增刊2)：41-46. Wang Jiyang，Lou Wenjuan，Tanaka Hitosh. Influence of Opening Type on Seismic Behavior of Reinforced Concrete Structural Walls[J]. Journal of Building Structures，2009，30(S2)：41-46.

[6] 付善春，孙春蕾，渠 强.开洞对剪力墙刚度及侧移的影响[J].洛阳理工学院学报：自然科学版，2013，23(3)：35-40. Fu Shanchun，Sun Chunlei，Qu Qiang. Influence of Openings on Stiffness and Lateral Displacement of Shear Wall[J]. Journal of Luoyang Institute of Science and Technology：Natural Science Edition，2013，23(3)：35-40.

[7] 陆新征，江见鲸.利用ANSYS Solid 65单元分析复杂应力条件下的混凝土结构[J].建筑结构，2003，33(6)：22-24. Lu Xinzheng，Jiang Jianjing. Analysis for Concrete Structure Under Complex Stress Condition with Solid 65 FEA Element of ANSYS[J]. Building Structure，2003，33 (6)：22-24.

[8]徐 巍，周 喆.对ANSYS的Link 8杆单元的几何非线性性能的评述[J].中国农业大学学报，2005，10(3)：111-114. Xu Wei，Zhou Zhe. Review on Geometric Non-Linear Performance of ANSYS’ Link 8 Element[J]. Journal of China Agricultural University，2005，10(3)：111-114.

[9] 中华人民共和国住房和城乡建设部.GB 50010—2010混凝土结构设计规范[S].北京：中国建筑工业出版社，2010：35. Ministry of Housing and Urban-Rural Development of the People's Republic of China. GB 50010—2010 Code for Concrete Structure Design[S].Beijing：China Architecture & Building Press，2010：35.

（责任编辑：邓光辉）

Finite Element Analysis on Mechanical Properties of Short Pier Shear Wall with Openings Under Monotonic Loading

Liu Xing，Yang Xiaohua，Chen Duanyun，Lu Nan
（Schools of Civil Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

In order to study the effect of the opening hole on mechanical properties of L shaped short pier shear wall, applies ANSYS finite element software to investigate the mechanical properties of short pier shear wall of different opening rates under the unchanged cross-sectional dimensions and reinforcement rates of the wall, and analyzes the bearing capacity and yield displacement. The simulated results show that the bearing capacity decreases with the openings rate increment and the bottom of the web as well as the opening position of the short pier shear wall are the weakest. Opening holes will reduce the mechanical properties of short pier shear walls under monotonic loading, and the opening diameter on short pier shear walls should not be too large.

short pier shear wall；openings rate；mechanical properties

TU312+.1

A

1673-9833(2015)02-0014-07

10.3969/j.issn.1673-9833.2015.02.003

2015-01-14

湖南省科技厅计划基金资助项目（2001TP4004-2），湖南工业大学研究生科研创新基金资助项目（CX1310）

刘 星（1991-）男，湖南长沙人，湖南工业大学硕士生，主要研究方向为混凝土结构及结构计算方法，E-mail：416107079@qq.com