基于主成分分析的ACA－BEM水下声辐射快速预报研究

刘金实

(江苏科技大学 船舶与海洋工程学院，江苏 镇江212003)

0 引 言

边界元法是水下结构振动声辐射预报的重要方法，与完全匹配层、无限单元法［1－3］相比，它具有直接求解开放声场、不需要在结构外部添加额外网格的优势，然而由于其系统矩阵为密集矩阵，随着问题规模的增加，其计算耗时和内存占用都迅速增长，因此如何降低边界元法的计算复杂度成了过去20年中学者研究的焦点，成果主要可分为两大类:以提高矩阵－向量乘积运算速度为目标的算法和矩阵压缩算法。前者以快速多极子边界元法［4］为代表，后者更接近于纯代数方法，以层级矩阵技术和自适应交叉近似算法为代表。由于快速多极子算法的程序实现受单元阶次的影响较大，多极子树的构建依赖于模型的几何特征，在工程应用中难以推广。

层级矩阵的核心思想是对密集矩阵进行层层分割，将子块的位置、大小等信息按树状的数据结构加以保存，对于其中秩较低的子块进行奇异值分解(SVD)，保留其余分块的密集格式。在之后的数年中，该方法被应用于声场、电磁场问题的计算中。在层级矩阵的基础上，Bebendorf［5］于2004年提出了自适应交叉近似(ACA)算法，该算法主要从2个方面完善并改进了层级矩阵法，首先是利用交叉近似方法对矩阵中的低秩子块进行逼近，替代了SVD算法，从而降低了对矩阵进行压缩的计算复杂度，其次是通过考察积分核的退化特性使算法具备了自适应的能力。Grasedyck［6］在交叉逼近的过程中引入了参考行和参考列以改进ACA 算法的逼近策略，避免了原有算法在少数情况下崩溃的风险，也使得ACA 算法的收敛速度有了轻微提高，同时首次将ACA 算法应用于边界元的快速计算，形成了ACA－BEM 方法。郑昌军等［7］将ACA－BEM 应用于声灵敏度的计算中，实现了声场问题最优化的快速计算。

1 理论基础

1.1 低秩近似理论

假设一个秩为k的矩阵M∈Cm×n，M的R(k)矩阵低秩近似可用因式分解的形式表示为:

其中U∈Cm×k;V∈Cn×k。式(1)也可更方便地表示为:

经过式(1)的分解，存储M 所需的内存空间由O(m × n)变为O(k × (m + n))，设有任意向量t∈Cn×1，则利用式(2)计算M × t，所需的浮点数乘法操作次数也由O(m × n)变为O(k × (m + n))。如图1所示，当M的秩远小于其维数时，利用式(1)可以显著降低其存储空间，并提高M × t的运算效率。

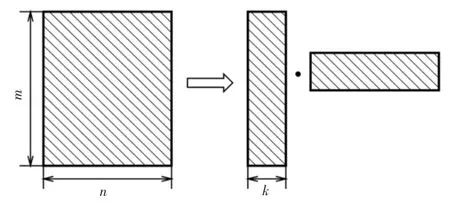
图1 矩阵分解示意图Fig.1 Diagrammatic sketch of matrix decomposition

然而在实际应用中，精确求出M的秩需要较大的计算量，会使得近似失去意义，为此须引入ε－秩及最佳近似概念:

其中M的最佳近似矩阵N∈Cm×n;rank(N)=k;‖…‖代表矩阵的范数。

1.2 自适应交叉近似算法

现有非零矩阵M∈Cm×n，且其所有元素的值均为已知。全选主元交叉近似算法首先利用以下步骤找出矩阵M的秩为1的近似矩阵M1:

1)确定M 中模值最大的元素所在行、列，记为i1和j1，并设δ=Miljl;

2)取出矩阵M 中第i1行和第j1列的向量，存储矩阵U*的第一列u1=M，j1，矩阵V*的第一行v1=Mi1，/δ。

则矩阵M1=U*V*。设整数p:1 ≤p ≤k，设第p步逼近完成后的余项为Rp，则将Rp作为第p+1步逼近的目标，从而形成如式(4)所示的关系。

在每一步逼近结束时，都可利用式(5)考察误差阈值是否已得到满足。

1.3 自适应交叉近似算法

准备阶段:输入矩阵M∈Cm×n，记‖M‖2= τ，设定收敛误差阈值ε，定义近似矩阵的Frobenius 范数为F0，随机生成整数il，满足1≤il≤m，设已使用的行坐标集合D={i1};

1)设定迭代计数p = 1，计算矩阵M的第i1行向量Mi1，*，确定Mi1，*中模值最大的列坐标j1，即j1=argmax(Mi1，*)，以及该元素的值δ=Mi1，j1;

2)计算出M的第j1列，记为M*，j1，根据式(6)得到逼近向量u1和v1:

3)利用式(7)更新逼近矩阵的Frobenius 范数:

4)利用式(8)判别逼近是否已经满足误差阈值的要求，若满足则跳转至步骤8)，否则继续执行步骤5)。

5)D=D ∪{ip}，根据列向量up从{1，…，m}/D 中选取行坐标ip+1，即ip+1=argmax(up)，计算Mip+1，*，利用式(9)计算余项矩阵第ip+1行作为逼近向量vp+1。

6)令jp+1=argmax(vi+1)，根据式(10)计算R*，jp+1，取出交叉点的余项值δ=Rip+1，jp+1，若δ 则终止循环，跳转至8)，否则利用式(11)计算逼近向量up+1。

7)利用式(12)更新逼近矩阵的Frobenius 范数并跳转至步骤4)。

8)利用式(13)给出矩阵U*∈Cm×p和V*∈Cp×n，算法终止。

图2 交叉近似示意图Fig.2 Diagrammatic sketch of cross approximation

1.4 基于主成分分析(PCA)的求解域分割

由于边界元矩阵中的行、列坐标都对应了网格中的各个节点，而矩阵的子块则代表着2个节点子集之间的相互作用，因此要将ACA 算法应用于对边界元矩阵的压缩，首先应根据几何相容性条件对求解域进行分割，得到若干节点集，通过将节点集之间的相互作用映射为边界元矩阵中的分块，利用几何相容性条件即可对子块的低秩特性进行预判。

文献［8－9］中较为常用的笛卡尔坐标系分割法，其思路较为简单，即首先找到包围求解域的最小长方体，长方体的各个面均与笛卡尔坐标系的坐标轴垂直，然后沿着3个坐标轴对长方体进行多级等分，直到所得到的子区域足够小或者满足几何相容条件。当求解域为二维空间中的一个圆时，分割结果如图3所示。

图3 圆形求解域分割示意图Fig.3 Schematic diagram of splitting circular solving domain

根据积分核退化理论［5］，设几何相容参数η=，则由图3 可看出，当包围求解域的长方体接近于正方体时，利用笛卡尔坐标系分割法得到的子块之间几乎都满足几何相容条件。然而当求解域为一个长宽比为4的长方形时，笛卡尔坐标系分割结果如图4(a)所示，其中a与c、b与d 之间均不满足几何相容条件，但如果只沿长方形的长边进行分割，如图4(b)所示，则任意2个不同子块之间都满足几何相容条件。由此可见，对求解域的分割方式影响着ACA 算法的压缩效果，进而可能影响到ACA 边界元法整体的计算效率。

实际分析中考察的模型既可能是如图3和图4 一样的形状规则，更多情况下也可能是各种不规则的形状，因此必须通过找到一种适应不同形状的求解域分割算法来提高子块间满足几何相容条件的概率。主 成 分 分 析［10］(Principle Component Analysis，PCA)又被称为主分量分析。利用主成分分析对数据进行处理，可以从影响问题的多个变量中选出影响较大的少数变量，这种思想在图像分析甚至经济学等领域有着广泛的应用。为了说明PCA 在分割边界元求解域中的应用，首先考虑一个二维空间中点集z，包含的节点数为n，节点分布如图5所示，其中节点i∈［1，n］的坐标记为zi，z的几何中心坐标为Cz，则z的主方向w的定义由下式给出:

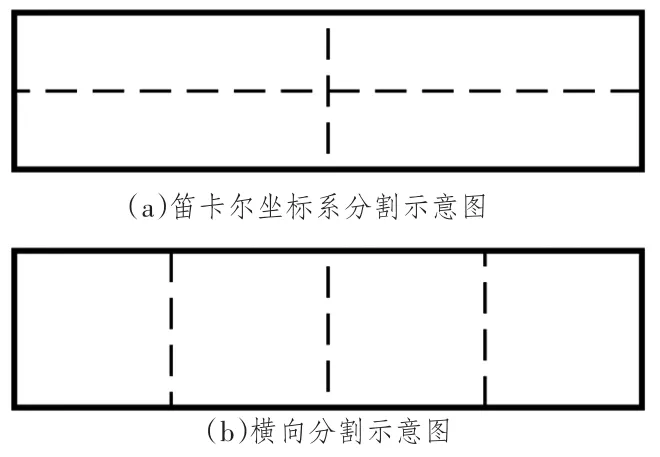
图4 横向分割示意图和笛卡尔坐标系分割示意图Fig.4 Subdivision of horizontal splitting and subdivision of cartesian splitting

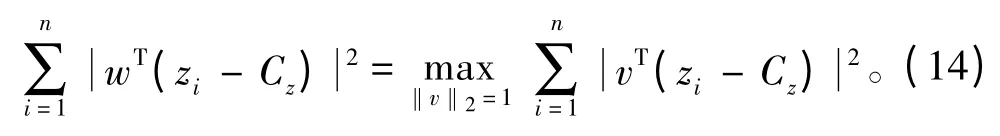
其中v为任意单位向量。在实际计算中可通过计算ZTZ最大特征值所对应的特征向量得到主方向向量w，即:

图5 笛卡尔坐标系分割和主成分分析法分割Fig.5 Subdivision of cartesian splitting and subdivision of PCA splitting

将w 作为坐标轴，得到z 中各点的坐标，在坐标值的最大、最小值的中心处取与w 垂直的分割面d，将z 分割为两部分，如图5(b)所示。

在对网格进行逐级分割的过程中，需要重复计算ZTZ 及其特征值、特征向量，相对于传统方法引入了额外的计算量，但由于在同一模型的各个分析工况间并不需要重复运算，因此不会对边界元分析的整体计算复杂度造成影响。

2 数值仿真

2.1 算法验证

为了验证ACA 边界元法的有效性，分析算法各参数设置对计算精度与效率的影响以及迭代求解器的收敛性能，本节采用圆柱壳作为验证模型，其中球壳半径为1 m，圆柱壳长为2 m，半径0.3 m，模型外部介质声速为1 500 m/s，密度为1 000 kg/m3。模型的形心坐标为(0，0，0)，且圆柱壳的轴向与z轴平行。统一设定求解域分割的最小子块含节点数不低于100，误差参数ε=10－6。

利用映射网格划分方法，将模型划分为746 节点、744个四边形单元的网格，设定所有节点沿外法线方向的振速为1，在(10，0，0)出设置一个声压观测点。分别利用传统边界元法和ACA 边界元法计算声压观测点处的辐射声压级，结果的误差曲线如图6所示。

图6 圆柱壳模型辐射声压级对比图Fig.6 Comparison of radiate sound pressure level for cylindrical shell

由图6 可看出，当误差控制参数设定为ε=10－6时，ACA－BEM与传统边界元法的预报结果具有很好的一致性。

2.2 计算效率分析

除了2.1 节中的圆柱壳模型，本节还考虑一个半径为1 m、厚度为0.003 m的水下球壳模型，将2个模型分别划分8 组不同密度的网格，如表1所示。令模型表面所有节点的振速为1 m/s，求解器内存占用和计算耗时曲线如图7和图8所示。

表1 网格规模表Tab.1 Table of mesh sizes

图7 内存占用量对比图Fig.7 Comparison of BEM matrices memory cost

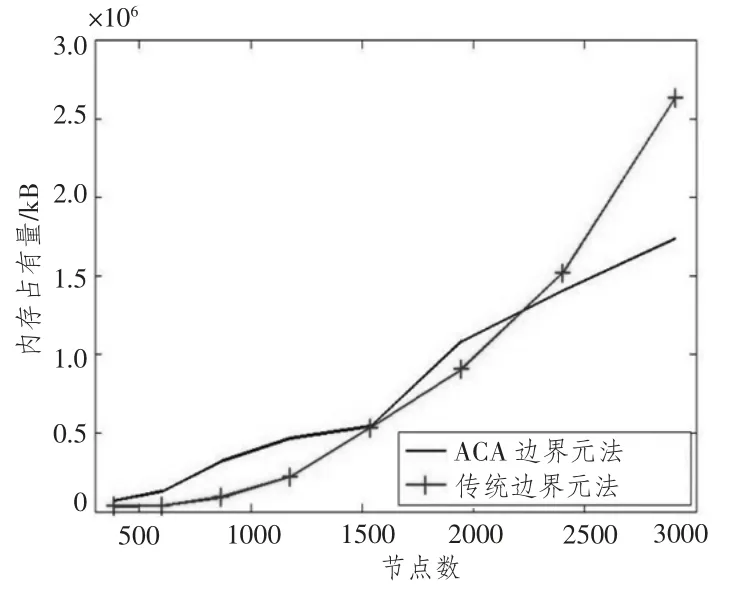
图8 求解耗时对比图Fig.8 Comparison of solving time cost

由图7和图8 可看出，由于采用了迭代求解器，ACA 边界元法的求解器只需要额外存储预条件矩阵的稀疏LU 分解因子，而对密集矩阵的LU 分解，分解因子和原矩阵本身的规模基本一致，因此在求解器的内存占用量上，ACA 边界元法具有较大的优势;从增长趋势来看，ACA 边界元法的求解运算耗时随节点数的增长速度显著缓于传统边界元法，但在网格节点数小于2 000 时并未显现出优势，主要原因是传统边界元法的求解过程中计算量最大的LU分解采用了LAPACK 标准函数，运行时的调度优化水平很高，而迭代求解器中矩阵与向量的乘法操作被替代为大量小型矩阵与向量相乘，虽然每次小矩阵与向量相乘都采用了优化程度较高的BLAS 标准子程序，能够调动CPU 所有计算核心并行运算，但每个线程的运行时间都非常短，频繁的线程切换浪费了大量的时间，据笔者观察，在计算程序运行过程中，CPU的峰值占用量不足35%。因此，通过改进计算程序的并行方式，充分利用机器资源，还可以较大幅度的提高计算程序的效率。

3 结 语

1)采用ACA－BEM 算法替代传统边界元法，并利用主成分分析法分割求解域，建立圆柱壳体模型，利用均匀脉动壳体问题验证了方法的有效性和准确性。

2)对比了ACA－BEM和传统边界元法在不同模型尺寸比、不同网格规模条件下的计算效率和内存占用量。ACA－BEM的计算效率受结构长宽比的影响较小，当节点数不足2000 时，ACA－BEM的计算效率与传统边界元相比不具备优势，但随着节点数的继续增多，ACA－BEM 在计算效率和内存占用量两方面都显现出明显的优势。

［1］JEAN P B.A perfectly matched layer for the absorption of electromagnetic waves ［J］.Journal of Computational Physics，1994，114(2):185－200.

［2］LUC C，FYFE K R，COYETTE J P.A variable order infinite acoustic wave envelope element［J］.Journal of Sound and Vibration，1994，171(4):483－508.

［3］BURNETT D S.A three-dimensional acoustic infinite element based on a prolate spheroidal multipole expansion［J］.Journal of Acoustic Society of America，1996，96:2798－2816.

［4］MICHAEL－A E，DEMBART B.Multipole translation theory for the three-dimensional laplace and helmholtz equations［J］.SIAM Journal on Scientific Computing，1995，16(4):865－897.

［5］MARIO B，RJASANOW S.Adaptive low-rank approximation of collocation matrices［J］.Computing，2003，70(1):1－24.

［6］LARS G.Adaptive recompression of－matrices for BEM［J］.Computing，2005，74(3):205－223.

［7］郑昌军，陈磊磊，陈海波.基于自适应交叉近似边界元法的快速声学灵敏度分析［J］.计算力学学报，2014(4):413－418.

［8］吴君辉，曹祥玉，袁浩波，等.自适应交叉近似算法在矩量法中的应用［J］.空军工程大学学报(自然科学版)，2013(5):76－79.

［9］杨剑.半空间环境中的自适应交叉近似方法研究［D］.西安:西安电子科技大学，2013.

［10］Ian Jolliffe.Principal component analysis［M］.Wiley Online Library，2005.