一种改进的纯方位目标运动分析方法研究

舒象兰，孙荣光，马 鑫

(海军潜艇学院，山东 青岛266042)

0 引 言

纯方位目标运动分析是指利用观测器获取的一系列目标方位测量信息估计目标运动参数的方法，它通常被广泛地用于海洋、航空和航天等领域中，特别是对于水下潜艇而言，纯方位目标运动分析是潜艇隐蔽攻击最基本的目标运动参数估计方法，其重要性不言而喻，然而，纯方位目标运动分析又是公认的世界性难题，代表着跟踪算法研究最具挑战性的领域［1－2］。影响纯方位目标运动分析方法跟踪性能的因素很多，其中观测方位的准确度对估计性能的影响至关重要，因为观测器测量的目标方位是纯方位目标运动分析唯一可利用的信息，往往随着观测器测量方位误差的增加，纯方位目标运动分析性能急速下降，这方面已经引起了广泛关注［3－4］。

事实上，在观测器测量的目标方位序列当中，不同时刻的方位测量准确度对纯方位目标运动分析跟踪性能的影响不同。其中，初始时刻的观测方位对于整个目标运动参数估计的影响显得极为突出，这是因为初始时刻的目标方位不仅会影响到目标的初始距离、航向、速度等运动参数的估计，而且作为目标航迹推算的起点，它对整个跟踪性能产生极其重要的影响，因此，目标初始时刻的方位是一个需要准确估计的参数，而不能直接将观测器的观测值作为目标的初始方位。

本文分析了观测器观测目标初始方位的准确度对纯方位目标运动分析跟踪性能的重要影响。在此基础之上，基于匹配场处理思想提出一种改进的纯方位目标运动分析方法，该方法将目标的初始方位作为待估计量，在目标初始方位可能的空间内进行搜索，构成多个滤波器估计出不同目标初始方位下对应的目标运动参数，并分别推算出目标方位序列作为预测场，根据推算的目标方位序列与实际观测的目标方位序列的匹配性确定目标的实际初始方位，从而实现对目标速度、航向、初始距离、初始方位四要素的完整估计。

1 初方位准确度对纯方位TMA 性能影响

假定目标作等速直航，且与观测器处于同一平面内，在此设x 轴指向正东，y 轴指向正北，目标初始时刻的状态为:X0=［vmx，vmy，D0］，由于假设目标匀速直航，因此，由初始状态便可唯一确定目标的运动轨迹。纯方位目标运动分析的任务就是依据观测器观测到的目标方位序列:B=［β0，β1，β2，…，βN］估计目标的初始状态，从而保持对目标的实时跟踪。设观测器的速度为vw(t)，航向为cw(t)且已知，定义vwx=vwsincw，vwy=vwcoscw，则在相对坐标系中，目标方位与定义参数之间的关系为:

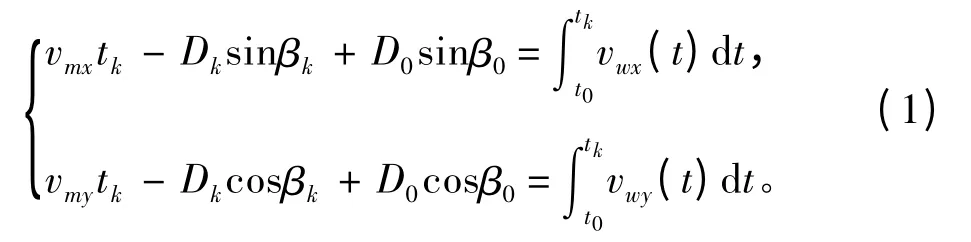
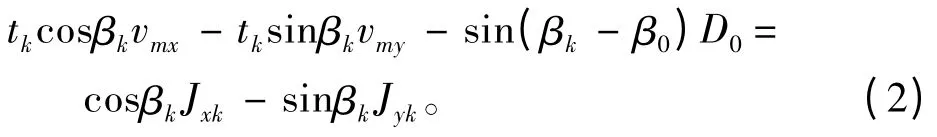
由于观测器方位观测误差的存在，对于该问题，可采用最小二乘方法估计得到:

其中，

式中:Sk=cosβk·Jxk－sinβk·Jyk，从而可得到参数vmx，vmy，D0的估计。

以上是传统意义上采用最小二乘估计解决纯方位目标运动分析问题的基本原理，在该方法中，直接将观测器在时刻t0观测到的方位作为目标的初始方位。从式(3)可看出，参数β0在矩阵A 中是一个极为重要的参数，它会影响到目标参数的估计。另外，β0作为目标航迹推算的起点，会影响到目标运动轨迹的推算，进而影响目标的跟踪。

仿真分析目标初始方位对纯方位目标运动分析性能具有重要影响。仿真条件为:假设目标作匀速直线运动，且速度为12 kn，航向为160°，与观测平台初始距离为20 km，相对于观测平台的实际初方位为20°;观测平台作匀速运动，在时间段(0，300)s 内，航向为20°，在时间段(300，1 000)s内，航向为320°，在时间段(1 000，1 800)s 内，航向为120°;目标保持匀速直线运动，速度为12 kn，航向为160°;观测平台对目标方位观测误差服从零均值、方差为0.5°的高斯分布，此处的3个仿真结果假设目标初方位分别为20°，21°，22°，其他时刻的方位都一样。图1 给出了纯方位目标运动分析的跟踪结果，其中，初方位20°时的距离估计相对误差为5.2%，初方位21°时的距离估计相对误差为34.7%，初方位20°时的距离估计相对误差为53.6%。

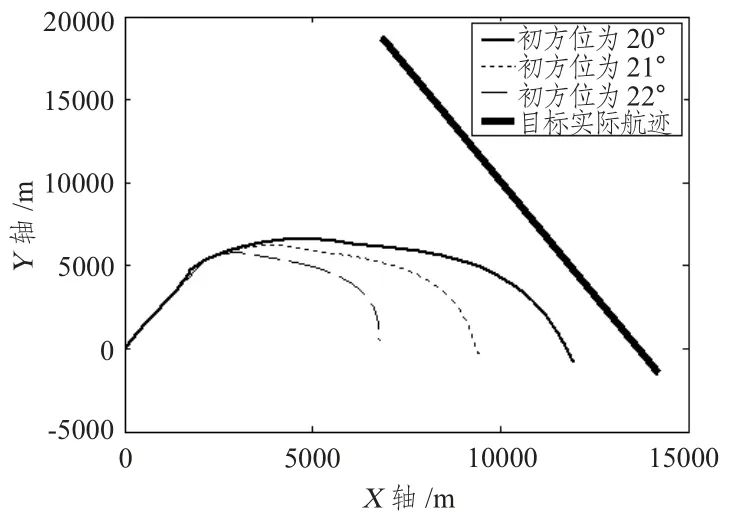
图1 初方位误差对纯方位目标运动分析性能的影响Fig.1 The bearing estimation error caused by multipath effect

从仿真结果可以看出，目标初始方位的准确度对纯方位目标运动分析跟踪性能影响极其显著。然而，观测器测量目标方位时的误差客观存在，假设观测器的方位观测误差服从零均值、方差为δ2的高斯分布，那么目标的实际初始方位可能会在范围［β0－3δ2，β0+3δ2］内，在此范围之内将会对跟踪性能产生极大影响，因此，直接将观测到的目标方位作为推算的初始方位不合理，它是一个需要准确估计的重要参量。

2 改进的纯方位TMA 方法原理

本文初始方位匹配的基本思想是:在目标初始方位可能的空间内进行搜索，构成多个纯方位滤波器估计出不同目标初始方位下对应的目标运动参数，根据估计出的目标运动参数可分别推算出相应的目标方位序列，并以此作为预测场，根据观测到的目标方位序列(观测场)与预测场的匹配性确定最优的目标初始方位，则该初始方位对应的目标运动参数就是最优的估计，从而实现目标速度、航向、初始距离、初始方位四要素的完整估计。图2为初方位匹配方法的原理图。

设观测到的目标方位序列为:Bm=［βm0，βm1，βm2，…，βmN］，假设观测器的方位观测误差服从零均值、方差为δ2的高斯分布，那么观测到的目标初始方位βm(0)可能会在范围［β0(0)－3δ2，β0(0)+3δ2］内，采用穷举法进行搜索，即在目标初方位可能的范围内，每隔一定的间隔Δ 抽样一次构成一滤波器，由于本方法只在一维空间内搜索，且搜索的空间较小，因此，采用穷举法也不会产生过大的计算量。

设根据第i个滤波器估计的目标运动参数推算的目标方位序列表示为:

将匹配函数定义为理论推算的目标方位序列与实际观测目标方位序列的“距离”，即:

则J(i)的最小化就意味着观测场与预测场的“距离”最近，从而便可得到i的最优解:

根据匹配函数(8)的最小值确定最优的目标初始方位，从而实现对目标速度、航向、初始距离、初始方位的完整估计。

3 仿真分析

首先仿真分析本文方法与传统纯方位目标运动分析在跟踪精度上的差别。仿真条件为:假设目标保持匀速直线运动，初始距离为20 km，速度为12 kn，航向为160°，速度为12 kn，相对于观测平台的实际初方位为20°;观测平台作匀速运动，在时间段(0，300)s 内，航 向20°，在时间段(300，1 000)s 内，航向320°，在时间段(1 000，1 800)s内，航向120°;观测平台对目标方位观测误差服从零均值、方差为0.5°的高斯分布;则采用传统的纯方位目标运动分析和本文方法得到的跟踪结果如图3所示。仿真结果显示，采用本文方法估计出目标的初始方位为19.9°，在稳定跟踪时的距离估计误差为，而传统纯方位方法在稳定跟踪时的距离估计误差为。可见，当观测初始方位误差较大时，本文方法仍能较准确估计出目标的真实初方位，从而使得跟踪的精度较高。

图2 多途效应导致方位估计误差示意图Fig.2 The bearing estimation error caused by multipath effect

跟踪的稳定性是考察跟踪算法性能的重要指标之一，在此，仿真比较本文方法与传统纯方位目标运动分析在跟踪稳定性上的差别。仿真条件与前面一致，仿真次数为500 次。传统纯方位目标运动分析方法直接将t0时刻观测到的方位作为初方位进行目标运动参数的估计，这就使得该方法的跟踪性能会随着初始时刻方位观测误差发生较大变化，跟踪的稳定性较差，如图4所示，在500 次仿真计算中，跟踪误差的起伏较大，其均方根差为1679.4。本文方法由于对目标初方位进行估计，将初方位误差对跟踪性能的影响降到最小，跟踪的稳定性较好，500 次仿真试验的估计方差为105.4。

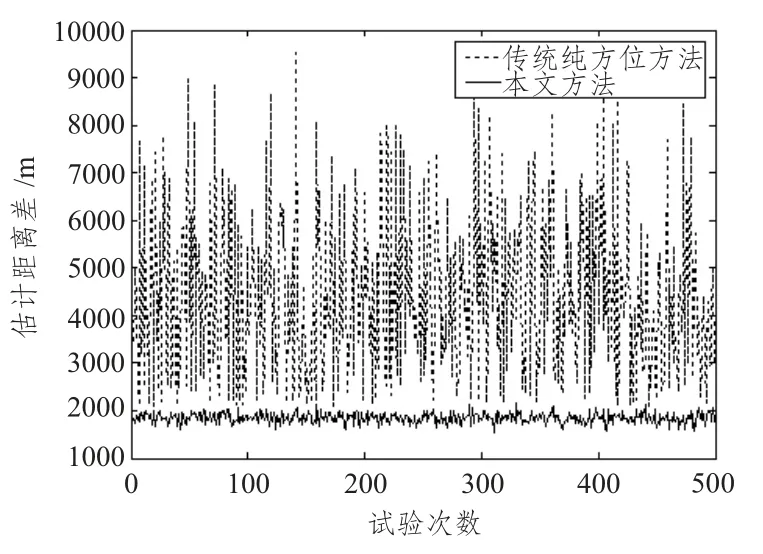
图3 本文方法与传统纯方位TMA 跟踪稳定性的差异Fig.3 The relation between bearing estimation error and angle of incidence

4 结 语

本文分析了观测器观测目标初始方位的准确度对纯方位目标运动分析跟踪性能的重要影响，并基于匹配场处理的思想提出了一种改进的纯方位目标运动分析方法，该方法将目标的初始方位作为待估计量，在目标初始方位可能的空间内进行搜索，构成多个滤波器估计出不同目标初始方位下对应的目标运动参数，并分别推算出目标方位序列作为预测场，根据推算的目标方位序列与实际观测的目标方位序列的匹配性确定目标的实际初始方位，从而实现对目标速度、航向、初始距离、初始方位四要素的完整估计。仿真结果表明，本文方法能够有效提高纯方位目标运动分析方法跟踪的精度以及稳定性。本文所研究方法的计算量较小，一般的PC 机就能完成相应的计算量，在无需明显增大计算量的情况下改善纯方位目标运动分析的性能，可工程化性较好，具有一定的应用前景。

［1］潘志坚，阎福旺，刘孟庵，等.纯方位水下目标运动分析方法研究［J］.声学学报，1997，22(1):87－92.PAN Zhi-jian，YAN Fu-wang，LIU Meng-an，et al.Method for bearings-only underwater target motion analysis［J］.Acta Acustica，1997，22(1):87－92.

［2］何友，关欣，衣晓.纯方位二维运动目标的不可观测性问题研究［J］.系统工程与电子技术，2003，25(1):12－14.HE You，GUAN Xin，YI Xiao.Research on the unobservability problem for two dimensional tracking based on bearings only measurments［J］.Systems Engineering and Electronics，2003，25(1):12－14.

［3］SHAR P，GONG X F.A practical approach to observability of bearing-only target tracking［J］.SPIE Proc，on Signal and Data Processing of Small Target，Denver，1999，7.

［4］夏佩伦.纯方位目标跟踪系统的可观测程度［J］.火力与指挥控制，1992，17(2):25－31.

［5］STOICA P，BESSON O，BESSON O.Direction of arrival estimation of an amplitude-distorted wavefront［C］//IEEE Transactions on Signal Processing，2001，49(2).

［6］BISHOP A N，ANDERSON B D O，FIDAN B，et al.Bearing-only localization using geometrically constrained optimization［J］.IEEE Transactioins otl Aerospace and Electronic systems，2009，45(1):308－320.

［7］ZHONG Zhi-tong，YANG Xiu-ting.The applications of nonlinear Kalman filters in passive tracking with bearing-only measurements［J］.Technical Acoustics，2008，27(6):912－916.

［8］DOGANCAY K.Bias compensation for the bearings-only pseudo linear target track estimator［J］.IEEE Transactioins on Signal Processing，2006，54(1):59－68.

［9］BAVENCOFF F，VANPEPERSTRAETE J M.Constrained bearings-only target motion analysis via markov chain monte carlo methods［J］.IEEE AES，2006，42(4):1240－1263.