基于LZW优化算法的雷达数据压缩技术

刘 林

(中国人民解放军91202 部队，辽宁 葫芦岛125004)

0 引 言

雷达在工作过程中，需要将前端雷达探测到的各种信号数据传输到后端进行处理，并且由于雷达探测数据的敏感性，一般要求将其探测的全部数据传输到后端，这就对雷达数据传输的信道带宽提出了较高要求，然而由于雷达实际工作过程中的各种限制，导致雷达数据传输信道容量有限，比如建设在某些高山、海岛等地的远程无人值守雷达，其数据传输到后端可能要经过多重无线、有线信道，由于这些信道带宽都受到限制，不能保证雷达数据传输的完整性和实时性。针对这种情况，要保证雷达数据传输的完整性和实时性，除了提高信道带宽以外，还可以采用数据压缩技术，对雷达数据在传输之前进行无损压缩，使之满足传输信道的要求，同时也能保证其完整性和实时性。

目前应用较为广泛的数据无损压缩技术有LZW编码、霍夫曼编码、算术编码和游程编码。其中LZW 编码是一种字典压缩算法，其在编、解码过程中动态形成字典，适用于各种不同类型的数据压缩领域［1］，因此其得到了广泛应用。在对该算法的实际编程过程中发现，该算法运行过程中的大量时间花费在对字典的检索过程。而对于雷达数据传输来说，数据传输要具备尽可能高的实时性，基于这点考虑，文中提出一种利用哈希表来优化LZW 编码的数据结构，从而有效减少LZW 算法字典检索时间的新方法，提升压缩效率，以尽可能提高雷达数据传输的实时性。最后，通过雷达数据压缩试验来验证该优化算法的有效性。

1 LZW 算法及改进

1.1 算法概况

1984年，TA Welch 对LZ 编码中的LZ78 算法改进而成为LZW 压缩算法。与费诺编码和霍夫曼编码相比，LZW 算法在使用过程中不需要对信源进行概率统计，与游程编码相比，其能够实现对不同但重复出现字符串的编码，并且LZW 算法还具有编码速度快和数据压缩效果更好的优点，因此其在实际中应用非常广泛。

LZW 算法通过使用一个串表将输入字符串映射成一个固定长度的码字输出来实现数据的压缩。在编程时，码字长度一般为12 位，也可以设置为15 位或者18 位。在压缩过程中，串表具有“前缀性”，即假若一个字符串由两部分构成，前部分为字符串S，后部分为字符C，若该字符串SC 存在串表中，那么C 就为S的扩展，S为C的前缀。在编码前首先通过初始化使串表包含所有的单字符串，然后进行压缩，压缩过程中串表不断产生压缩信息的新字符串，同时必须保存新字符串SC的前缀S 相对应的码字。当进行数据解压缩时，解码器可以根据编码字恢复出同样的字符串表，从而实现编码数据流的解码过程［2－5］。

1.2 算法流程

依据上述对LZW 算法的描述，在实现LZW 算法编程时，按照图1 进行。

1.3 算法应用

下边通过分析一个简单的数据压缩实例来说明LZW 算法的具体实施过程。现有一个字母表a，b，c，d和一个输入字符流:“abacaba”，下面给出该字符流压缩的实施步骤。

步骤1:对串表进行初始化，有0 = a，1 = b，2 = c，3 = d，前缀S = 空。

步骤2:读当前字符，有C = a，则SC = a，因为字符串a 包含在串表中，则S = a。

图1 LZW 算法流程图Fig.1 LZW algorithm float chart

步骤3:读取第2个字符，有C = b，则SC =ab，该字符串不包含在串表中，则添加SC 到串表中，有4 = ab，且同时输出S(也就是a)的索引0 到编码流，然后修改S = b;

步骤4:读下一个字符，有C = a，则SC = ba，该字符串不包含在串表中，则添加到串表中，有5 = ba，输出S的索引1 到编码流，修改S = a;

步骤5:读下一个字符，有C = c，则SC = ac，该字符串不包含在串表中，则添加到串表中，有6 = ac，输出S的索引0 到编码流，修改S = c;

步骤6:读下一个字符，有C = a，则SC = ca，该字符串不包含在串表中，则添加到串表中，有7 = ca，输出S的索引2 到编码流，修改S = a;

步骤7:读下一个字符，有C = b，则SC = ab，该字符串包含在串表中，且4 = ab，则修改S = ab;

步骤8:读下一个字符，有C = a，则SC = aba，该字符串不包含在串表中，则添加到串表中，有8 = aba，输出S的索引4 到编码流，修改S = a;

步骤9:再一次读取字符时发现字符读取完毕，即没有需要压缩的数据，则输出S的值a的索引0到编码流，

步骤10:编码结束，输出结果:010240。

表1 中记录了上述各步骤变量的属性图。表中加粗行的项为在串表中找到了相关表项后的操作。

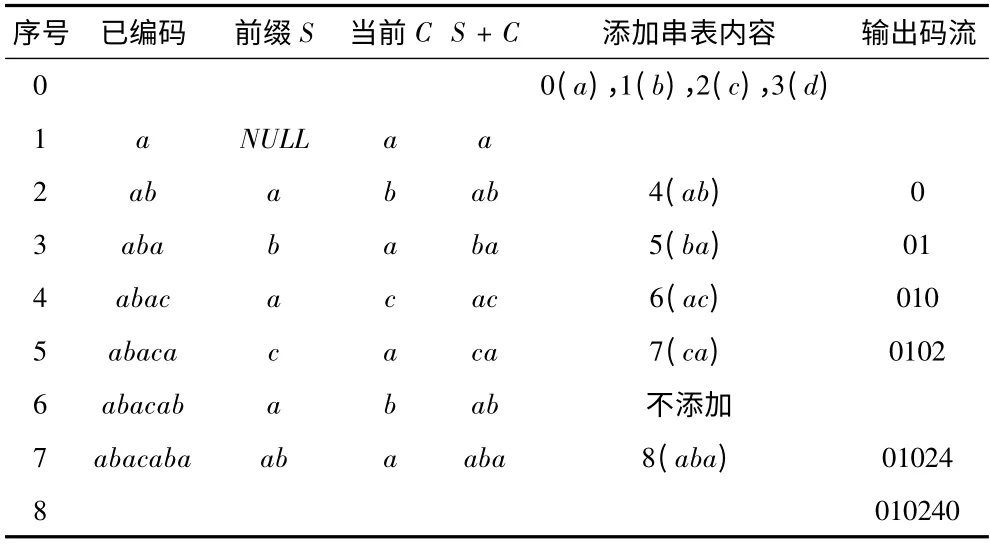
表1 LZW 编码实例属性图Tab.1 LZW encoding instance attributes

1.4 算法改进

如果设置码长为12 位，那么串表个数为:212=4 096。而在对每一个字节进行编码时，都需要对整个串表进行搜索和字符对比，因此LZW 算法的大部分时间用于对串表进行搜索，造成了LZW 算法实时性不强，难以应用于高实时性数据压缩场合。而雷达数据压缩就是一个高实时性要求的应用场合，为了能够将LZW 算法用于雷达数据压缩领域，就必须对该算法进行改进，提高其实时性，以满足雷达数据压缩的要求。LZW 算法的大部分时间用于串表的遍历，因此可以考虑提高其遍历效率来提高实时性。在软件设计过程中，采用树型数据结构相对串表可以大幅提高遍历效率，但是树型结构同样需要遍历，并且算法复杂度和稳定性不够好。提高遍历效率最好的方式就是不进行遍历，能够直接通过位置关键字进行查找，这是最为理想的方式，从这个角度出发，可以采取将记录存储的位置和关键字进行对应，从而通过查找关键字来直接寻址到存储的数据。

在软件编程领域，哈希表就可以实现上述想法。哈希表其实就是一个特殊二维数组，这里记编码字符值范围为0～255，则12 位码长编码的哈希表可以记为M［4096］［256］，且矩阵M［i］［j］中行号i表示前缀在串表中的索引号，列号j 表示当前字符，则M［i］［j］的值为前缀和当前字符组合在串表中的索引，如果串表中不包含该项，则M［i］［j］=－1。该设计方法具有如下优点:

1)通过使用串表中的索引来实现前缀而不再需要另外建立一个数组。

下面使用3 种不同类型的文件数据来进行LZW算法压缩试验，文件数据类型分别为64 kB图像文件、30 MB 雷达数据文件和800 kB 文本文件，3 种文件均采用原始LZW 算法和改进LZW 算法分别进行10 次试验，然后求消耗时间平均值。将其数据记录于表2。从表中记录数据可以看出，LZW 算法在经过使用哈希表优化后，其编码效率提升80%以上，效果很明显。因此该算法具有很高的实用性，能够大幅提高压缩效率，节约大量时间，满足某些高实时性要求场合的数据压缩需求。

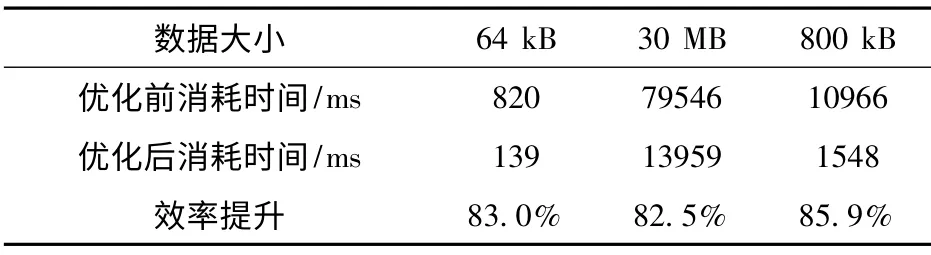
表2 LZW 算法优化前后效率对比Tab.2 Efficiency comparison of LZW algorithm

2 雷达数据压缩试验

下面采用实际雷达数据对该算法进行测试。这里选取3 种不同的雷达数据:1 类为杂波较多的256灰度级雷达数据;2 类为杂波较少的256 灰度级雷达数据;3 类为二值雷达数据。为了更好地检验算法提升效率，实测时选取不同长度的编码单位进行编码，并且将其结果和游程编码进行对比。LZW 算法测试数据记录于表3，游程编码测试数据记录于表4。为了更加直观的观察算法的提升效率，将两表中数据采用压缩比计算公式:

压缩比=压缩前数据大小/压缩后数据大小换算成压缩比数值，然后将该数值绘制于同一张坐标图中，如图2所示。

表4 游程编码3 种类型雷达数据压缩效果Tab.4 Radar data compression effect of RLC algorithm for three types data

图2 三种数据类型不同压缩单元LZW和游程压缩比变化曲线Fig.2 Compression ratio of LZW and RLC for three kinds of different data

分析表3和表4 中的数据以及图2 中2 种编码方式对照图，可以得出如下结论:

1)LZW 算法的压缩比对编码单元长度大小十分敏感，其压缩比大小随编码单元长度增加而增加，符合前边的理论推导，理论上，当编码单元长度无穷大时，LZW 算法可趋于最优的编码效率。而游程编码对编码单元长度不敏感，其压缩比稳定在一个范围内。

2)当数据类型不同时，其压缩比随之变动较大，由表中数据可得出，1 类型数据的压缩比为2左右，而2 类型数据和3 类型数据的压缩比可达到几十倍左右，并且LZW 算法在具有较大长度编码单元时具有明显优势。

综述以上结论，LZW 算法在使用过程中有以下注重点:

1)LZW 算法在编码单元较小时不具有优势，而当具有较大的编码单元时，LZW 算法的压缩效率提升非常迅速。

2)在LZW 算法中，串表的个数将直接影响算法的编码效率，因此，为了获得更好的编码效果，可以通过改变串表个数来协调编码效率和系统内存及时间的消耗。如何通过选择串表个数来达到编码效率和系统消耗之间的平衡，这将需要更进一步的研究和总结。

3 结 语

LZW 算法是一种性能优异的数据无损压缩算法，广泛应用于各种数据压缩领域。本文将该算法用于压缩雷达信号数据，针对雷达数据量庞大以及该算法实时性难以满足要求的问题，通过分析发现该算法的大部分时间用于串表搜索过程，据此，提出利用哈希表数据结构来简化其搜索过程，提高算法编码速度，从而满足雷达数据压缩的实时性需求。最后通过雷达数据压缩对比试验，验证对该算法改进的有效性和提出实际运用该改进算法的几点参考意见。

［1］柳楠，赵秀梅，张志军.基于LZW 压缩的图像信息隐藏方法［J］.计算机应用与软件，2007，24(8):193－195.

［2］郭晓岩，郝永胜.LZW 无损压缩算法在计算机取证中的应用研究［J］.测控技术，2006，25(11):64－67.

［3］张凤林，刘思峰.一个改进的LZW 数据压缩算法［J］.小型微型计算机系统，2006，27(10):1897－1999.

［4］蓝波，林小竹，籍俊伟.一种改进的LZW 算法在图像编码中的应用［J］.计算机工程与科学，2006，28(6):55－57.

［5］林小竹，籍俊伟.一种改进的LZW 压缩算法［J］.计算机工程，2005，31(14):199－201.

［6］王泉，齐春，罗新民，梁嵩.LZW 压缩算法的改进及其参数优化分析［J］.重庆邮电学院学报(自然科学版)，2005，17(3):351－371.

［7］崔业勤，刘玉贵.基于LZW的多模式自适应的无损压缩算法［J］.微电子学与计算机，2005，22(3):99－105.

［8］王平.LZW 无损压缩算法的实现与研究［J］.计算机工程，2002，28(7):98－150.