系列舵翼潜艇水动力系数数值计算及试验研究

王庆云，庞永杰，李伟坡，廖欢欢

(哈尔滨工程大学水下机器人技术重点实验室，黑龙江 哈尔滨150001)

0 引 言

潜艇是世界各海洋大国特别重视的武器装备，也是衡量一个国家海军强大与否的标志之一，潜艇作战时，操纵性能的良好也是战争取胜的关键因素之一，在潜艇初步设计阶段，需要对其操纵性能进行评估和预报，以便完成潜艇在水下的运动控制仿真和调试工作，精确获得构成潜艇六自由度操纵运动方程的水动力系数是基础工作。

当前潜艇水动力系数的获得主要有2 种方式:一是通过平面运动机构(PMM)拘束模型试验获得。美国国防等研究计划署提出的SUBOFF［1］项目，在泰勒水池对所提出的3 套不同舵翼同一主艇体SUBOFF 进行研究，并形成了详细的水动力试验报告［1］，为潜艇数值模拟研究提供参考。二是通过CFD 软件求解稳态雷诺时均方程(RANS)和基于无界流面元法2 种方法获得［2］。学者们主要基于美国高等研究计划署提出的SUBOFF 项目进行数值模拟［3-5］，来验证自己对模拟方法选择的准确性。虽然在一定程度上取得了较好精度，但也只能完成常规运动的简单模拟。然而在潜艇设计中，主艇体确定以后，操纵面的布局及舵几何尺寸的选择对潜艇操纵性能起着至关重要的作用，很少有学者从舵面布局及尺寸方面进行模拟，所以对舵角试验开展也显得非常有工程价值。

本文基于STARCCM + 软件，对系列舵翼SUBOFF 潜艇完成了阻力性能模拟;利用基于三角网格的面元法计算程序完成系列舵翼潜艇附加质量的求解，得到3个潜艇的惯性类水动力导数，作为试验对比验证。此外，对系列舵翼SUBOFF 潜艇模型(λ =2∶1)展开斜航、纯升沉、纯俯仰、纯首摇、纯横荡试验，获取相应的水动力导数，同时系列改变流速，研究其舵角水动力导数随Re的变化趋势［6-7］以及各舵翼之间舵角水动力导数的变化规律，并详细分析了试验误差来源。本实验水动力系数的获取为潜艇操纵预报和运动控制仿真提供数据支持和工程参考，并为CFD 技术进行操纵性预报提供验证参考。

1 系列舵翼SUBOFF 潜艇阻力数值计算

1.1 计算对象

所选计算模型总长4 356 mm，附体包括围壳和十字形舵翼，主艇体最大直径508 mm，3个舵翼布局及面积如图1所示。

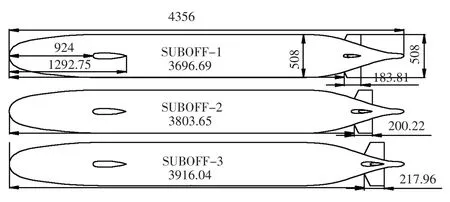
图1 系列舵翼SUBOFF模型几何尺寸(单位:mm)Fig.1 Geometry of SUBOFF model of a series of rudder and wing(unit:mm)

1.2 基本理论和数值方法

1.2.1 控制方程

雷诺时均Navier-Stokes 方程如下:

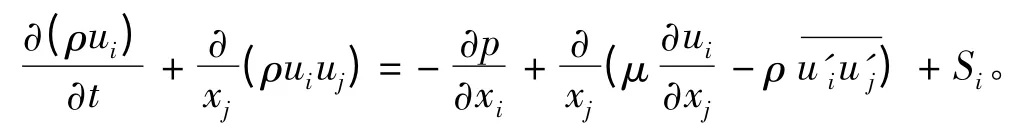
式中:i和j 取值范围是(1，2，3);ui为时均速度;u′为脉动速度;为雷应力。

采用SST k-ω 湍流模型封闭雷诺时均方程［4］，近壁面流体采用壁面函数法，STARCCM + 建议20＜y+＜100，使用SIMPLE 算法对压力速度耦合方程组进行求解，离散方程中粘性项采用二阶中心差分格式，对流项采用二阶迎风格式。

1.2.2 计算域设置和网格划分

船首、四周为1 倍艇长，船尾为3 倍艇长，边界条件来流方向和四周设置为速度入口，去流方向设置为压力出口。利用STARCCM +软件自动网格生成，采用切割体六面体网格自动完成SUBOFF潜艇网格的划分，逐步渐进的对船体周围网格进行加密，并在围壳及其尾十字舵周围进行网格加密，保证非加密与附近加密区网格尺寸相当，有利于计算插值和物理量的交换，加快收敛速度，网格总数160 万。图2 给出2个不同截面艇体周围网格示意图。

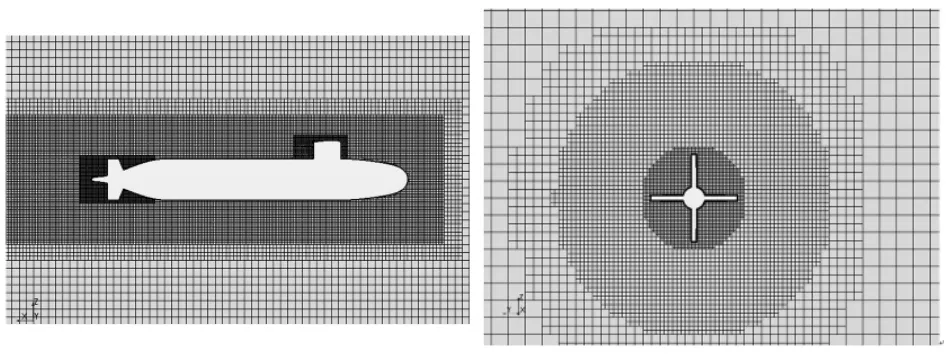
图2 SUBOFF模型周围计算域网格Fig.2 The grid of SUBOFF model around the field

1.3 结果与分析

非定常数值模拟中，时间步长满足Δt ≤u/Δl，其中u为航速，Δl为最小网格尺寸，每一时间步的最大迭代次数为5 次，近壁面y+≈50，边界层设置为5 层，增长比例1.2。计算结果如表1所示，SUBOFF-2与文献［1］值符合良好，平均误差为3.06%，Cf与8thITTC 推荐的标准式估算值相比［4］，平均误差为-1.55%，由此表明本文计算网格和方法的准确性。以此方法为准计算得到SUBOFF -1，SUBOFF-2 阻力值，如表2所示。

由表2 可以看出，随着舵翼的后移，舵翼面积增加，摩擦阻力SUBOFF-1，SUBOFF-2 摩擦阻力值相差较小，SUBOFF-3 摩擦阻力值最大，但摩擦阻力系数3个艇型接近相等，约为2.58E -03;压力与压力系数均表现为SUBOFF-2 最大，SUBOFF-3最小。就总阻力而言，依次增加，但SUBOFF -2，SUBOFF-3 总阻力相差较小，最大仅相差4.58 N，而SUBOFF-1，SUBOFF-2 总阻力最大相差为18.48 N，SUBOFF-1，SUBOFF-3 总阻力值最大相差23.06 N。可见，SUBFF-2，SUBOFF-3 阻力性能相当。

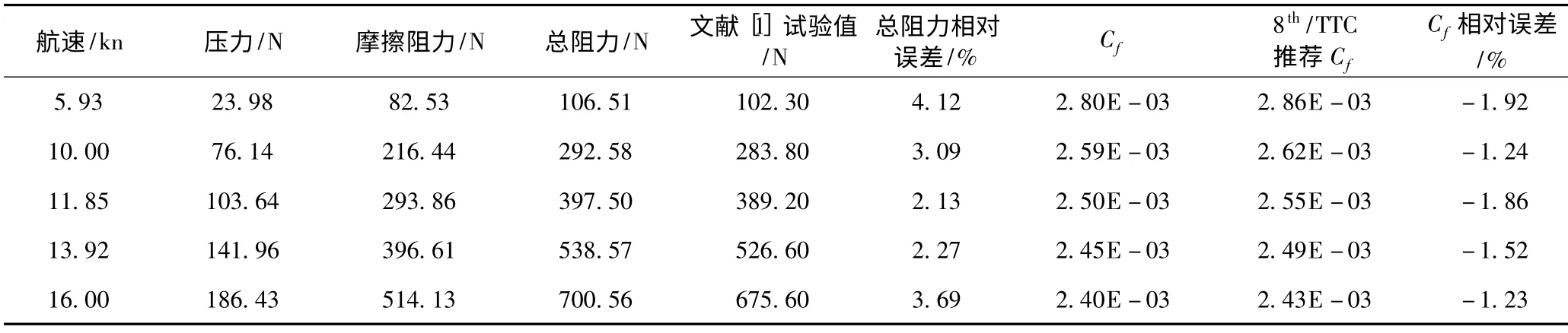
表1 SUBOFF-2 阻力计算结果Tab.1 The resistance calculation results of SUBOFF-2

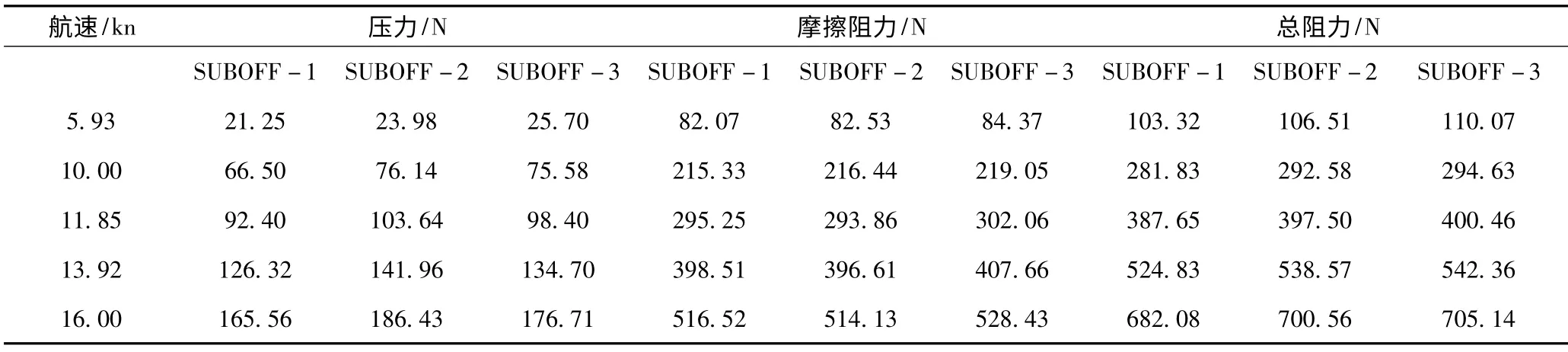
表2 系列舵翼SUBOFF 阻力计算结果Tab.2 The resistance calculation results of SUBOFF of a series of rudder and wing

2 系列舵翼SUBOFF 水动力试验及计算

2.1 基于面元法计算惯性类水动力导数

基于势流理论基本理论［2］，无界流中，在物面分布源汇，利用Hess-smith 方法求解关于源汇强度的积分方程，本文把物面Sh分成N 块三角面元:

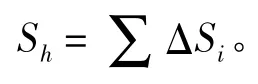
用平面三角形近似代替小曲面，面元中心点坐标为三角形点坐标的算术平均值。面元上的分布源密度在局部坐标系下表示为:

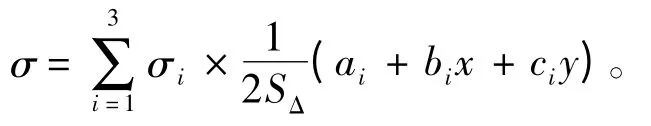
其中系数用三角形点坐标:

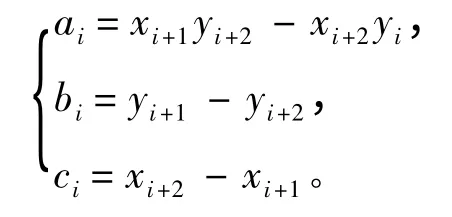
面元划分在Gambit 软件中进行，主艇体表面网格尺寸稍大，围壳和舵翼表面网格稍细，以便近似完全表真潜艇的几何形状，从而增加计算的精度，减少计算时间，本例总面元网格为5 500 左右，如图3所示。网格划分完成以后，从Gambit中导出* .neu 文件，导入面元法程序完成附加质量计算，计算得到作用在物体上的惯性类水动力导数，如表4所示。

图3 SUBOFF模型表面三角形网格Fig.3 The triangular grid surface on the hull of SUBOFF model

图4 SUBOFF模型安装于循环水槽中Fig.4 SUBOFF model installed in circulating water channel

2.2 系列舵翼潜艇模型水动力试验测量

本实验在哈尔滨工程大学水下机器人技术重点实验室循环水槽中进行，考虑到水槽尺寸的限制，采用缩比模型进行试验，缩尺比λ = 2，本模型最大长度为2 178 mm。考虑到非定常运动空模型内流对测力的精确性，就此在艇体内部填充足够的材料，同时保证潜艇入水良好的浮态(0 浮力，稳性高为0)。图4为SUBOFF 潜艇安装于水槽示意图，除舵角试验流速为系列流速平均值以外，其余试验流速均为1.035 m/s，水动力测试结果如表3所示。

1)从表3 中可以看出SUBOFF -2 水动力系数试验值与文献［1］值符合良好，粘性类水动力系数中Z′q相比文献［1］值较大，但仍然保持在10-3量级，正负号与文献［1］相反，其余水动力导数值与文献［1］相比，误差相对较小，均为同量级，符合良好;惯性类水动力导数本文面元法计算值与试验值中Z′q相差较大，表现为同一个量级，其余水动导数值符合较好，其中和接近文献［1］试验值的2 倍，所有惯性类水动力导数与文献［1］值为同量级;不同流速下获得的无因次舵角水动力导数平均值与文献［1］值偏小，Z′δs误差较大，为-24.6%，其余符合良好，误差来源主要有:①尺度效应，即模型缩比2∶1导致舵面积相对文献［1］小了一半，且文献［1］采用拖航试验拖航速度为3.344 m/s，而本实验在循环水槽中进行，试验最大流速1.456 m/s，测得的舵力相对较小;②本实验PMM 运动机构两支杆产生的尾流场导致艇体尾部流场与真实流场不符，导致无因次水动力导数值偏大;③试验仪器以及数据处理方面可能带来误差。

2)从表3 中所有水动力数值来看，本文试验数值、面元法计算值与文献［1］除个别水动力导数相差较大以外，总体符合良好，由此表明本文试验方法和基于三角网格面元法2 种方法得到的水动力导数基本能够满足工程应用，具有一定工程实用价值，有待进一步改善。对比SUBOFF -1，SUBOFF -2，SUBOFF-3的水动力导数可以看出，3个艇体惯性类水动力导数相差最大不超过10%;而3个艇体粘性水动力导数，除相差较大以外，其余粘性水动力导数SUBOFF - 2，SUBOFF - 3 接近相等，与SUBOFF -1 相差较大;而就舵角水动力系数而言，虽表现为同一个量级，以Z′δs相差最大，SUBOFF-1为SUBOFF -3的2.24 倍;且从SUBOFF1 -3，Y′δr成减小趋势，其余3个舵角水动力导数成增加趋势。

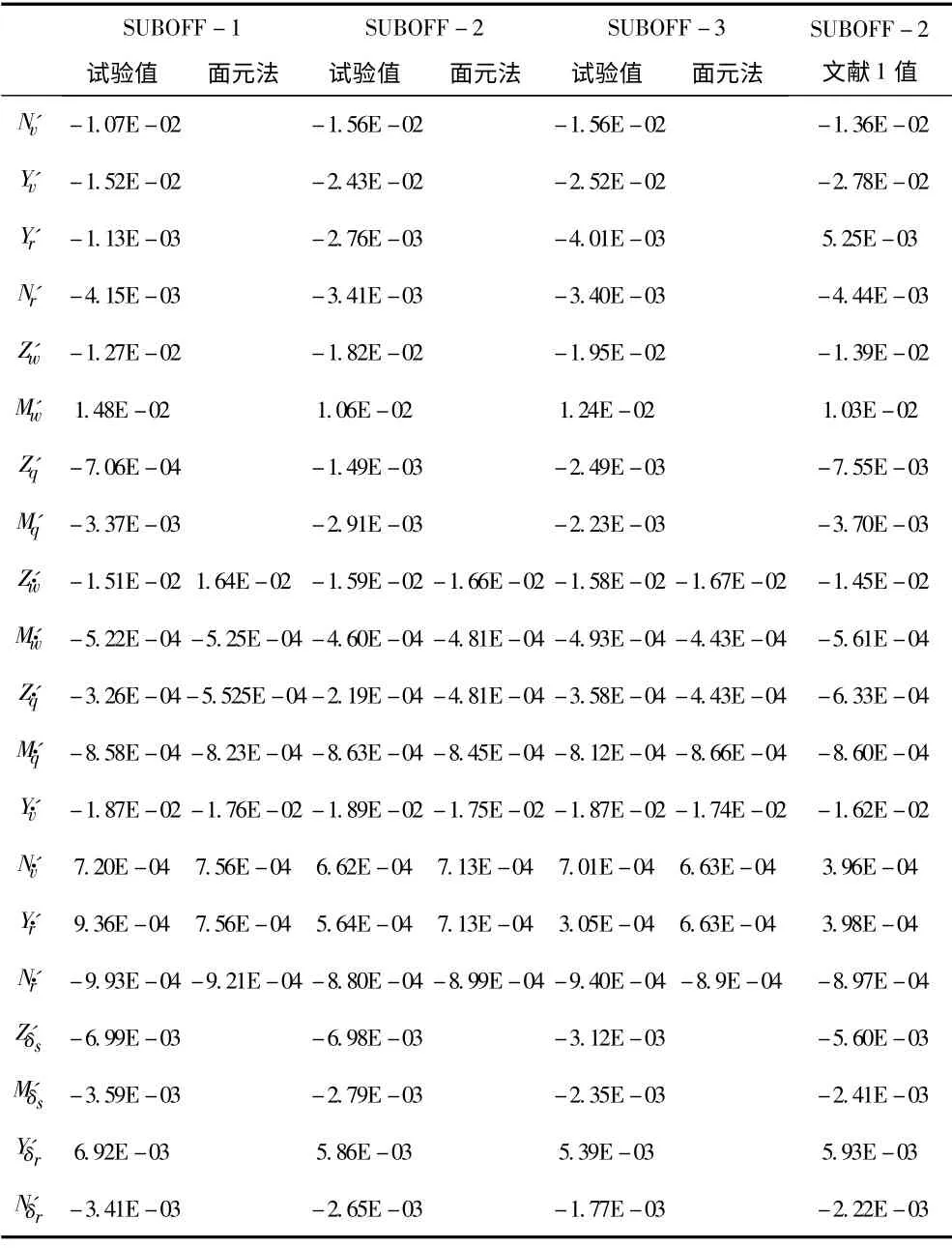
表3 系列舵翼SUBOFF模型水动力系数Tab.3 Hydrodynamic coefficients of SUBOFF model of a series of rudder and wing

2.3 雷诺数对舵角水动力导数的影响研究

舵角试验是潜艇在漂角和冲角为0的情况下，借助舵机操舵，系列改变循环水槽流速来获得作用在艇体上的力(力矩)［8］，求得相应的无因次舵角水动力导数，图5和图6 给出系列舵翼方向舵、升降舵舵角导数Y′δr，N′δr，Z′δs，M′δs随Re的变化情况。

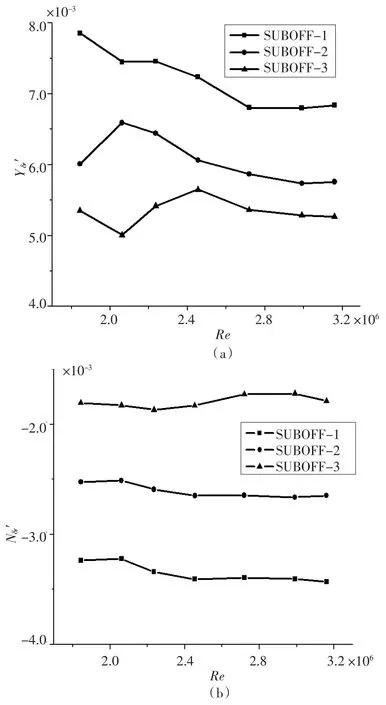
图5 水动力导数Y′δr，N′δr 随Re的变化趋势Fig.5 Variation tendency of the hydrodynamic coefficients Y′δr，N′δr as a function of Reynolds number

1)从图5和图6 中可以看出，随着Re 增加，Z′δs和Y′δr值较N′δr和M′δs不稳定，且Y′δr稳定性比Z′δs差，表明随着流速的增加，测力天平两支杆的尾流场对Z′δs和Y′δr为影响大于N′δr和M′δs，然而对Y′δr影响最大，故在以后试验过程中，建议在垂直安装模型时选择对升降舵舵力的测量，在水平面安装模型时选择对方向舵舵力的测量，以此减少支杆的影响;从1 号舵翼到3 号舵翼，舵位置后移，面积增加，同一Re 下，无因次舵角导数Y′δr逐渐减小，差距逐渐缩小;无因次舵角导数N′δr反而逐渐增加，差距变化不大;无因次舵角导数M′δs也成增加趋势，差距逐渐缩小;无因次舵角导数Z′δs也基本表现为增加趋势，差距逐渐增大。

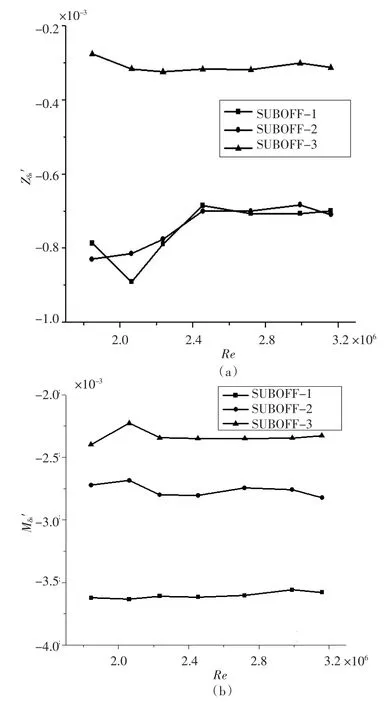
图6 水动力导数Z′δs，M′δs 随Re的变化Fig.6 Variation tendency of the hydrodynamic coefficients Z′δs，M′δs as a function of Reynolds number

2)从图5和图6 中可以看出，当Re 在2.4 ×106之前，即对应流速为1.1 m/s 之前时，舵角水动力导数变化相对较大，之后趋于稳定，但当Re为3.2 ×106，对应流速为1.5 m/s 时，舵角水动力导数又表现出不稳定的情况，故可初步判定在此循环水槽中进行水动力系数测定时，流速应该保持在1.1 m/s～1.5 m/s 之间较为合适。从此判定可以推断前文选择流速为1.035 m/s 进行水动力试验并不是最佳状态，为此验证了前文水动力系数误差偏大的原因之一，这也为今后利用此循环水槽进行水动力系数测试的试验提供了依据。同时验证了在超过临界雷诺数下，当流速保持在一定范围时，舵角水动力导数趋于稳定，也为水下航行器舵翼的设计和CFD 数值模拟提供了参考依据。

3 结 语

本文以文献中的SUBOFF模型为研究对象，对不同舵翼同一主艇体、围壳的3个标准潜艇完成阻力数值模拟;利用基于势流理论的三角形网格面元法和试验的方法获取潜艇水动力导数;并在超过临界Re 数的情况下，研究了舵角水动力导数随Re 变化情况。与文献［1］对比，结果符合良好。结论如下:

1)基于切割六面体网格具有易生成性和自适应性，验证了STARCCM+软件对潜艇阻力性能模拟的可靠性，为后续潜体水动力CFD 数值模拟奠定了一定基础;系列舵翼潜艇中，SUBOFF-2，SUBOFF-3阻力性能表现基本一致。

2)三角形网格的面元法对潜艇惯性类水动力导数求解可靠，相比四边形面元网格，计算简单方便，且对于复杂几何模型三角面元网格较四边形面元网格较易生成;通过对水动力导数的获取，对比验证了本实验的可靠性，但还有待进一步改善。

3)系列舵翼潜艇舵角水动力系数相差较大，其余水动力系数除个别以外，SUBOFF-2，SUBOFF-3相差较小，表现基本一致;验证了循环水槽试验中，Re 在2.4 ×106后，舵角水动力导数趋于稳定，并且随着舵翼后移面积增加，除Y′δr减小以外，其余舵角水动力系数成增加趋势。为潜体舵翼的设计和布局提供了参考依据。

［1］RODDY R F.Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF Model［C］//Departmental Report.Ship Hydromechanics Department.David Taylor Research Center.Maryland，1990，9.

［2］张赫，庞永杰，李晔.潜水器水动力系数计算方法研究［J］.武汉理工大学学报，2011，33(1):15 -18.ZHANG He，PANG Yong-jie，LI Ye.Study of AUV′ s hydrodynamic coefficients calculation methods［J］.Journal of Wuhan University of Technology，2011，35(1):15 -18.

［3］RIDGES D H，BLANTON J N，BERWER W H，et al.Experimental investigation of the flow past a submarine at angle of draft［J］.AIAA Paper Journal，2003，41(1).

［4］PAN Yu-chun，ZHANG Huai-xin.Numerical prediction of submarine hydrodynamic coefficients using CFD simulation［J］.Journal of Hydrodynamic，2012，24(6):840 -847.

［5］杨琼芳，王永生，张志宏.全附体潜艇粘性流场的RANS模拟及场量和涡量的校验分析［J］.计算力学学报，2012，29(4):567 -572.YANG Qiong-fang，WANG Yong-sheng，ZHANG Zhi-hong.RANS simulation and check of vorticity and fields of viscous flow field of all possess submarine［J］.Journal of Computational Mechanics，2012，29(4):567 -572.

［6］柏铁朝，梁中刚，周轶美，等.数值计算有漂角时潜艇表面压力与水动力特性［C］//第五届中国CAE 工程分析技术年会论文集.

［7］孙铭泽，王永生，杨琼芳.潜艇操纵性数值模拟中雷诺数的影响分析［J］.哈尔滨工程大学学报，2012，33(11):1334 -1340.SUN Ming-ze，WANG Yong-sheng，YANG Qiong-fang.The effects of reynolds number analysis of submarine manoeuvrability numerical simulation［J］.Journal of Harbin Engineering University，2012，33(11):1334 -1340.

［8］丁正良，胡瑞芝，孙百超，等.水平型循环水槽的水动力性能［J］.船工科技，1983(4):1 -16.