土地收储项目风险评估的模糊综合评价模型

刘元志，朱家明

(1. 安徽财经大学经济学院，安徽，蚌埠 233030；2.安徽财经大学统计与应用数学学院，安徽，蚌埠 233030)

土地收储项目风险的评估[1]，用来评估项目可能带来的风险损失程度。其涉及财务风险、市场风险、运营风险和社会风险等多个维度，通过有效控制这些风险指标，可以完善土地收储制度，降低土地收储运营风险，实现土地收储可持续发展。国内研究还主要停留在理论层面，并未具体针对土地储备项目进行风险的综合评估。陈晓军[2]通过对西安某市土地储备项目的研究，利用不可修复可靠性串联模型与休哈特控制图建立预警控制界限，建立时间序列回归判别模型，得出多土地储备项目风险的波动与土地储备机构决策者的决策心理趋势。陈平[3]运用层次分析法和模糊综合评价法对某县土地储备中心的财务状况进行了评价，得出该储备机构的财务风险程度为中等水平。本文针对 74个土地储备项目，提取适当风险指标，构建土地收储项目风险评估的模糊综合评价模型，对项目进行风险评估（详见 2014年第七届“认证杯”数学建模网络挑战赛C题[4]）。

1 风险指标的选取及其权重的确定

1.1 风险指标的选取及解释

通过对土地储备项目可研报告中提取的数据进行分析，首先定义4个新的风险指标[5]：财务净现值率、动态回收周期、融资成功比率、人口密度相对数，分别用来替代财务风险、市场风险、经营风险和社会风险。其中财务净现值率=财务净现值/项目投资总额估算；动态回收周期：通过土地出让，收回收储成本所需的时间，一般以年计算；融资成功比率=银行批复额度/项目投资总额估算；人口密度相对数=涉及拆迁人口数/收购储备面积。

1.2 运用正态分布检验进行数据预处理

令X为上述4个指标在一个随机实验中被检测的结果，且这个结果取大量偶然因素的总和，淡化个别因素单独作用的影响，则X的分布就近似于正态分布[6]，其密度函数为：

特别 μ = 0 、 σ2=1为标准正态分布，记作 N ( 0,1)。取Z为标准正态变量，用z为其取值，则它的概率密度函数式为：

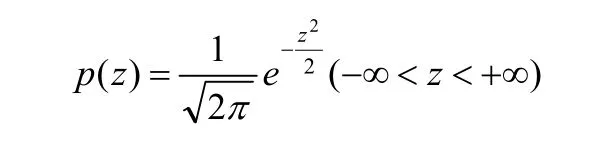
其中z∈[-5,5]的概率几乎为1。也就是说，z不属于[-5,5]的事件几乎不可能发生。

我们提取的 4个风险指标数据均服从正态分布，故可利用正态分布的性质对其进行检验。下面把随机变量的标准化，得：

运用Excel软件进行计算，可获取4个指标的标准化后的取值结果，见表1。

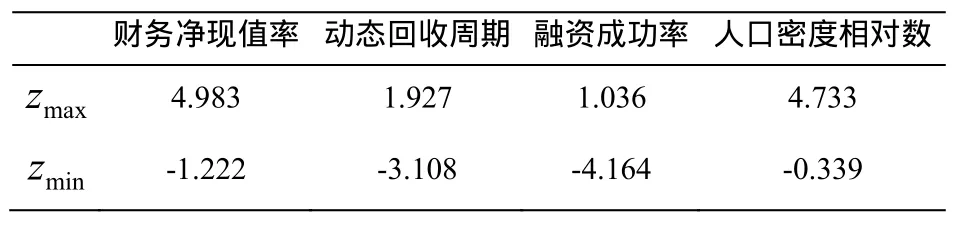
表1 四个指标对应的z值表Table 1 The four indicators of the corresponding Z value

由表1可发现，所有的z值均在 ]5,5[- 内，故正态分布检验没有发现数据异常。

1.3 风险指标权重的确定——层次分析法

1）研究思路

我们设定一种“等距分级，等比附值”的新模糊标度方法。首先采取Fuzzy AHP方法和新模糊标度进行求解。为了使定量的相对重要度a正确反映定性评判的结果，必须使判断尺度给出的相对重要性大小与定性分析的结果基本相符，这就要求判断尺度本身要符合一定的规则。现假设判断尺度符合“等距跃进”，则有：

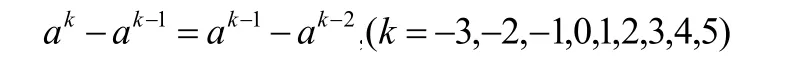
对上式进行计算得到 1=a ，显然这与判断尺度不符合，再假设判断尺度符合“阶梯跃进”，则有：

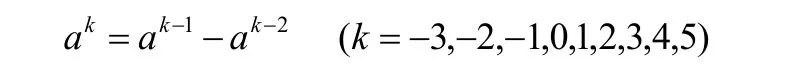
对上式进行计算得到 618.1=a ，这与合理性准则基本一致，这时有新的模糊标度，见表2。

表2 新模糊标度及其含义表Table 2 New fuzzy scale its meaning

2）模糊层次分析模型[7]的建立与求解

①风险评估中，针对风险度这一目标来说，可以分为三个层次，分别为目标层、准则层和项目层，详见图1。

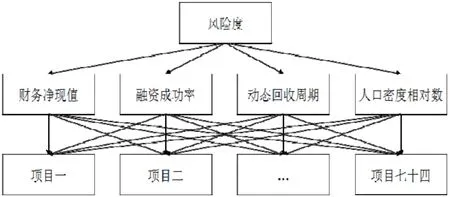
图1 层次分析的递阶层次结构图Fig.1 Hierarchy structure chart of hierarchical analysis

②在判断各个准则的重要性时，结合实际社会经验和调查的可研究报告，做出各个准则对项目重要性和影响力的合理判断。认为本题中的财务风险和经营风险是项目所承受的主要风险，故财务净现值率和融资成功率是重要程度较高的准则，故对起伏较大的权重，模糊判断矩阵如下：

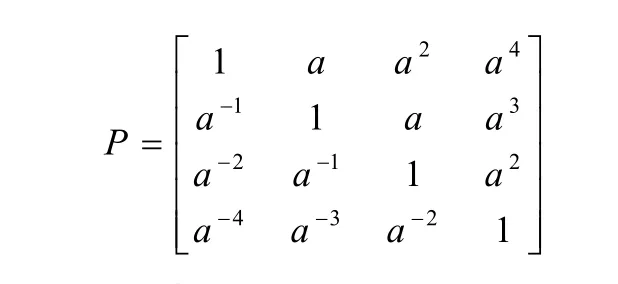
其次，利用特征向量法寻找出4个因素的权重向量。具体做法是：首先求出四个评价指标的相关系数矩阵R，然后求出各指标标准差所组成的对角矩阵 S，最后求出矩阵 RS的最大特征值所对应的特征向量，就得到各指标的权重向量。模糊判断矩阵P的最大特征值所组成的对角矩阵：

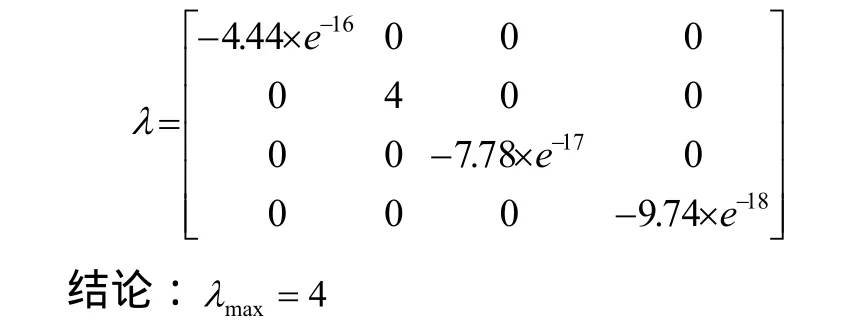
③由于客观事物的复杂性，可能会使我们的判断带有一定程度的主观片面性，所以需要进行一致性检验：

表3 一致性检验表Table 3 The consistency test table

当 n = 4时，查表可得 RI = 0.89，求得：CR = 0≤0.1。表明此模糊判别矩阵通过一致性检验。

④确定各指标权重

通过一致性检验，认为其比较矩阵的不一致程度在容许范围之内，故可用来计算权重。则每个准则的权重为：

表4 四个风险指标的权重Table 4 The four risk weight index

2 基于模糊综合评价法的项目风险分析

2.1 项目风险评估分析

在对项目进行评估时，其评估因素会有很多，不能仅依据一个指标的好坏就作出判断，应依据多种因素进行综合评价。对此我们分别采取模糊综合评价法[8]进行分析。首先，依据项目评价指标值建立模糊矩阵；再次，对模糊矩阵中数据进行加权求和；最后，将项目按其风险度大小进行排序。如果按降序排序，则项目越靠前，项目实施的风险越大，反之越小。

2.2 模型的建立与求解

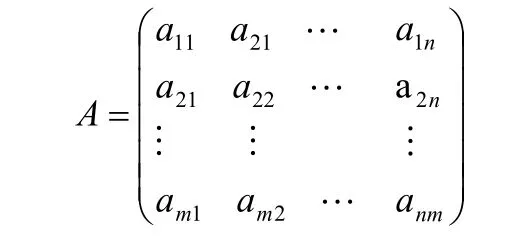
其中ija表示第j个项目关于第i项评价因素的指标值。

①建立理想项目：

③建立评价指标的权数 wij(i =1,2,…,n)

④建立综合评价模型：

2）利用EXCEL软件将数据进行处理后，得到了相对偏差模糊矩阵如下所示：

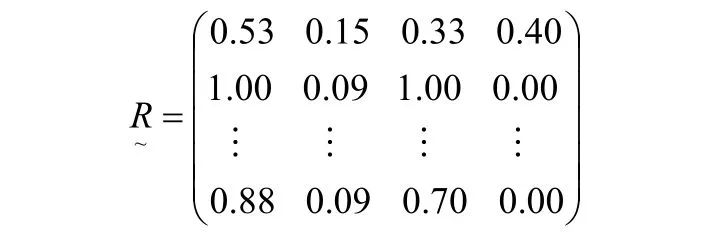
之后通过数据加权求和得到风险度，结论如表5所示。

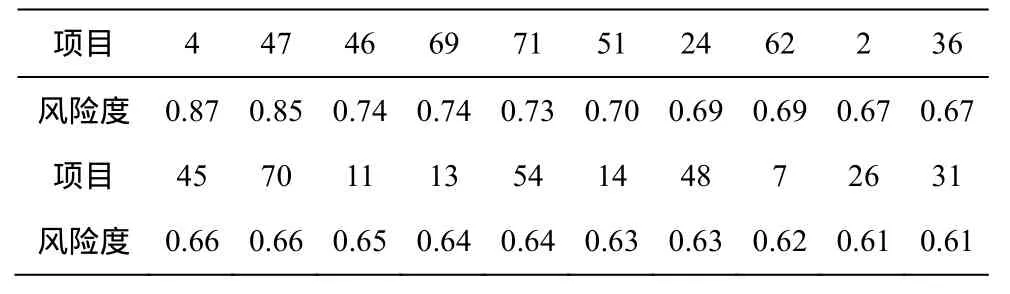
表5 项目风险排序表（取前20个项目）Table 5 The project risk ranking(taking the frist twenty items)

由表5可知，综合考虑财务风险、市场风险、运营风险和社会风险，项目总表中风险度最大的20个项目分别是：4，47，46，69，71，51，24，62，2，36，45，70，11，13，54，14，48，7，26，31。

3 运用残差分析处理异常项目

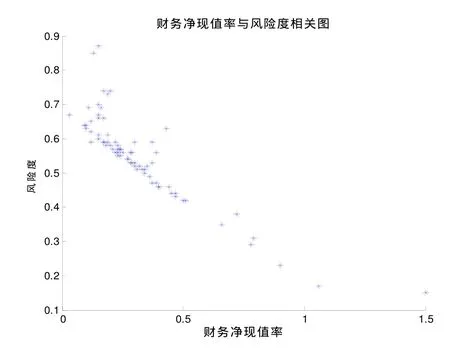
图2 财务净现值率与风险度的相关图Fig.2 Correlation diagram financial net present value rate and risk degree

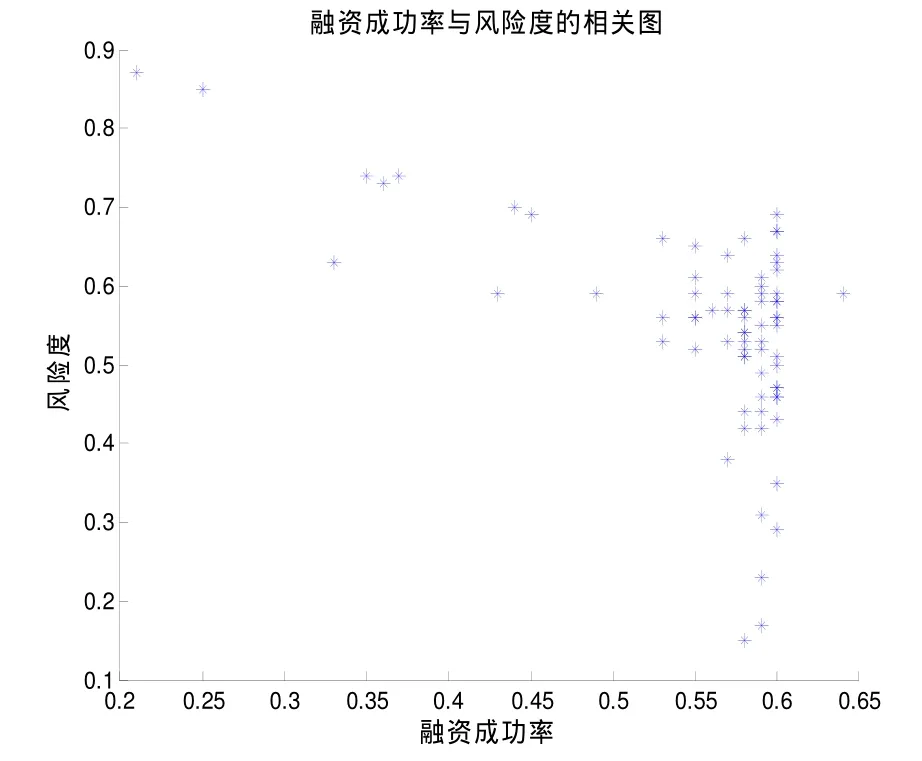
图4 融资成功率与风险度的相关图Fig.4 Financing success rate and correlation diagram of risk degree

3.1 研究思路

在数据预处理时，我们已经运用正态分布检验对单指标列数据进行了检验，没有发现异常数据。在综合考虑各个风险指标后，通过模糊综合评价模型给出了风险评估方法，即计算每个项目的风险度。此时，可以利用残差分析[9]，对各风险指标数据进一步进行检验，即对在残差分布表中置信带以外的数据进行分析。通过采用 Eviews软件，对前面求得的各个风险指标，作出与风险度之间的相关图，然后选择适当函数进行曲线拟合，并分析其残差分布表，进而分析分散在置信带以外的数据。

3.2 研究方法

1)作出各个指标和风险度的相关图，分析两变量间的关系。

图3 动态回收周期与风险度的相关图Fig.3 Correlation diagrams of dynamic recovery period and the degree of risk

图5 人口密度相对数与风险度的相关图Fig.5 The population density of relative number and related diagram of risk degree

2)分析以上相关图可知，融资成功率与风险度的相关图，和人口密度相对数与风险度的相关图落点比较分散，所以无法用函数有效地拟合出这些曲线，所以舍弃这两个指标不做分析。下面函数是对财务净现值率和动态回收周期两个指标进行拟合的结果。

财务净现值率与风险度拟合函数：

3)分析财务净现值率与风险度拟合函数残差分析表可知，需要剔除的数据所对应的项目序号为：4,46,47,48,49,57,69,71。

分析动态回收周期与风险度拟合函数残差分析表可知，需要剔除的数据所对应的项目序号为：4, 38,46,47,48,56,57,69,71。

综合两个指标可知，异常项目归类见表6：

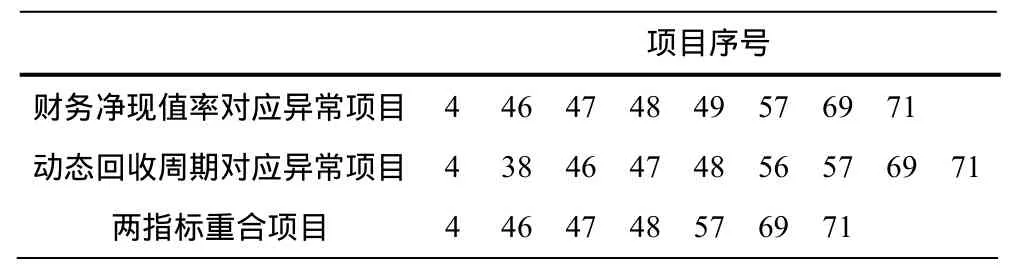
表6 相关指标离异值对应项目表Table 6 Correlation index value of the corresponding project divorced

4 总结

本文从正态分布检验、层次分析、残差分析、模糊数学等多个角度入手，运用了多种统计分析方法，并且也通过了各种检验尺度，得出了综合考虑财务风险、市场风险、运营风险和社会风险等风险因素的土地收储项目的风险评估方法。与其它方法相比，本文针对具体土地收储项目，结合实践所建立的模糊综合评价模型，更具有实用性和可操作性，通过具体指标综合分析并得出土地收储项目的风险程度。

[1] 吴虹,辛波. 基于因子分析的土地金融风险度量[J].井冈山大学学报:社会科学版,2014,35(1):69-73,98.

[2] 陈晓军,盛淑凯,张建利,等.土地储备项目风险预警控制模型[J].中国土地科学,2009,23(1):38-42.

[3] 陈平.土地储备的财务风险评价研究[D].成都:四川农业大学,2011.

[4] 2014年第七届“认证杯”数学中国数学建模网络挑战赛C题[EB/OL].http://www.doc88.com/p-0179378431658.html.2015-02-08.

[5] 朱家明,钟梅,张月茹,等.葡萄酒质量评价的定量分析[J],宜春学院学报,2013.35(3):8-12.

[6] 曾五一,肖红叶.统计学导论[M].北京:科学出版社，2013.

[7] 杨桂元,黄己立.数学建模 [M].合肥:中国科学技术大学出版社,2008.

[8] 李柏年,吴礼斌.度MATLAB数据分析法[M].北京:机械工业出版社,2012.

[9] 庞浩.计量经济学[M].北京:科学出版社,2010.