基于Simulink的水轮机调节系统仿真中水轮机模型研究
2015-12-06张成立秦正飞
高 磊,张成立,秦正飞,汪 健
(昆明理工大学冶金与能源工程学院,云南省昆明市 650093)
基于Simulink的水轮机调节系统仿真中水轮机模型研究
高 磊,张成立,秦正飞,汪 健
(昆明理工大学冶金与能源工程学院,云南省昆明市 650093)
基于Matlab/Simulink仿真工具建立的水轮机调节系统,有助于了解水轮机调节系统在实际运行过程中的调节过程。水轮机调节系统分为四部分,包括水轮机调速器、压力引水系统、水轮机以及发电机。本文介绍了各模型的一般形式,并主要就现有的几种水轮机模型进行总结和分析。
Simulink;仿真;水轮机调节系统;水轮机模型;非线性模型
1 概述
水轮机调节系统是由调速器、压力引水系统、水轮机、发电机及其所在电网四部分所组成的闭环控制系统,这是一个包含了水、机、电的综合控制系统。随着水电站仿真技术的不断发展,对水电机组建立数学模型进行仿真,可以经济、直观、迅速地研究其静态和动态特性,从而提高了研究效率。但是,水轮机调节系统是一个复杂的非线性系统,在建模过程中忽略一些次要因素从而得到简化模型。要想通过仿真来完全、准确地反映水轮机调节系统的实际过程并得到定量的结论是十分困难的,因此只能为实际工作提供定性的分析及决策支持[1-2]。由于水电站的不同特性以及复杂的工况,全面建立水轮机的各种状况下的动态模型并研究其使用范围具有重要意义,因此要了解模型的局限性和适用范围,可以在实际工程应用中选择正确的模型。
在现阶段中使用计算机数值解法建立的水轮机数学模型可以分为三大类:第一类是基于水轮机内特性的数学模型,即根据水轮机自身物理原理建立的水轮机数学模型;第二类是基于水轮机综合特性曲线的数学模型,在建模过程中以水轮机模型的综合特性曲线作为水轮机数值特性的边界条件;第三类是由美国IEEE Working Group提出的非线性水轮机模型[3]。
交互式仿真工具Simulink是一种图形化仿真工具包,是Matlab的重要组件之一,它拥有动态系统建模、仿真和综合分析,可处理线性、非线性系统,离散、连续和混合系统,以及单任务和多任务系统。Simulink提供建立模型方框图的用户接口,通过单击和鼠标拖动即可完成对模块的建立,为用户提供了直接快捷的建模和仿真方式,因此,用户可方便地进行上述操作而无需编写任何代码程序,大大提高仿真效率和可靠性[4]。
2 水轮机调节系统仿真模型
水轮机调节系统各模块的连接如图1所示。

图1 水轮机调节系统仿真框图
2.1 调速器模型
2.1.1 PID调节器模型
现在大型水轮机组的控制器一般都是由并联PID调节器和机械液压随动系统构成,本文也基于此种模型对调速器进行建模。PID控制策略是比例、微分、积分控制的综合作用,理想的PID调节器模型其传递函数为:
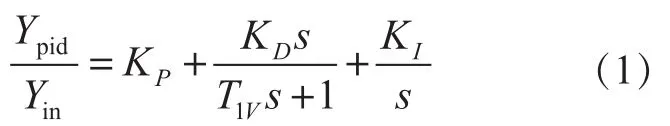
式中:KP,KI,KD分别为比例、积分、微分增益常数;T1V为微分衰减时间常数。
具体到水轮机调节系统,并联PID型调速器的模型结构如图2所示。
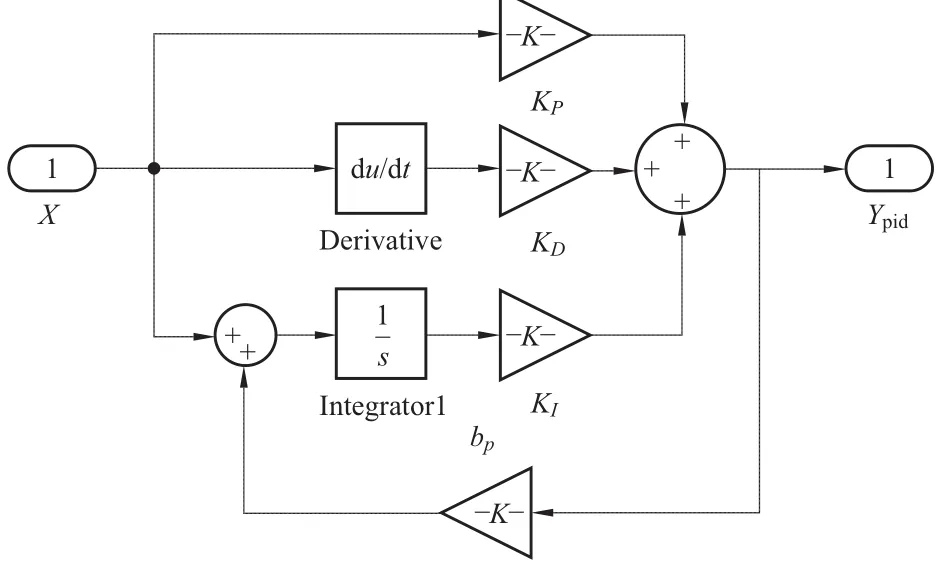
图2 调速器PID仿真模型
图2中bp为永态差值系数,其值在0~0.1之间整定,它的作用是在并列运行机组之间合理分配负荷。
2.1.2 随动系统模型
水轮机调节系统中紧接调速器的是随动系统。国内外水轮机型号众多,总结来看,主要有三种不同的随动系统结构:电液随动型、中间接力器型和辅助接力器型。在小波动工况下,接力器动作的速度和幅度都有限,当系统进入大波动工况时,液压环节的动作速度较快,幅度有可能超过到全行程位置,这时候必须考虑机械液压部件的非线性因素。本文选用电液随动型模型,该模型考虑了死区和饱和特性,则液压随动系统模型如图3所示。

图3 液压随动系统仿真模型
图3中Ty为主接力器时间常数(s)。
2.2 引水系统模型
实际的水电站压力引水系统如图4所示。
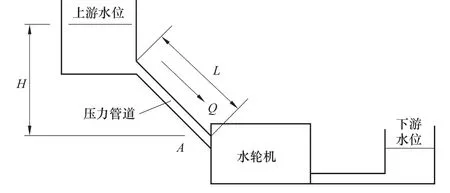
图4 压力引水系统结构示意图
2.2.1 弹性水击模型
引水管道较长时,弹性水击理论能更精确地描述管道动态过程。在忽略水流与水管壁之间摩擦以及尾水管影响的情况下,考虑水流及水管壁的弹性,由水力学原理中的动力方程和连续性方程可以导出弹性水击方程:
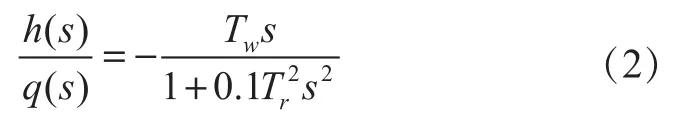
式中:Tw为水流惯性时间常数;Tr为管道反射时间常数。
2.2.2 刚性水击模型
在短引水系统中(一般认为其管道长度小于600~800m),水体及管壁的弹性对水锤的影响较小,可以用刚性水锤理论来描述压力引水系统的动态特性。则引水系统的刚性水击模型为:

2.3 发电机模型
当负载变化时,水轮发电机组的阻力矩会发生变化,从而引起机组转速的变化,因此,发电机也是调节对象的一个部分。单机系统带孤立负荷的运行情况,使用一阶模型即可满足仿真分析的需要。发电机及负荷模块的数学模型如下:

式中:Ta为机组惯性时间常数(s);en=eg-ex,其中ex为水轮机力矩对转速的偏导数,又称为水轮机自调节系数,eg为发电机(负荷)力矩对转速的偏导数,又称为发电机(负荷)自调节系数。
3 水轮机模型库
现提出的水轮机调节系统数学模型主要包括线性化模型和非线性模型。线性化模型具有物理意义清晰、结构简单等特点,但由于其采用近似化处理忽略了非线性特性,一般仅应用于小波动情况的研究。非线性模型能更好地反映水轮机调节系统的运动特性,随着非线性动力学理论的不断完善和计算机辅助计算能力的提升,在非线性模型的研究上有了重要的发展。
3.1 线性水轮机模型
流量Q和力矩Mt是水轮机的两个重要参数,一般根据水轮机的实验特性曲线,将力矩和流量表达为导叶开度a、转速n和水头H的函数。
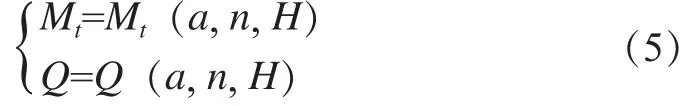
在扰动不大的情况下,可近似认为在工况点附近水轮机维持线性特性不变。将式(1)在工况点附近用泰勒级数展开,水轮机特性可用线性的力矩方程和流量方程表示为:
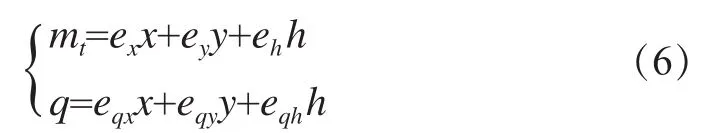
式中:ey为水轮机力矩对导叶开度传递系数;ex为水轮机力矩对转速传递系数;eh为水轮机力矩对水头传递系数;eqy为水轮机流量对导叶开度传递系数;eqx为水轮机流量对转速传递系数;eqh为水轮机流量对水头传递系数。
传递系数的求法一般是应用最小二乘法原理、做曲线求斜率法的差值计算,或有限差值近似计算方法。
在Simulink环境下建立引水系统和线性水轮机模型如图5所示。
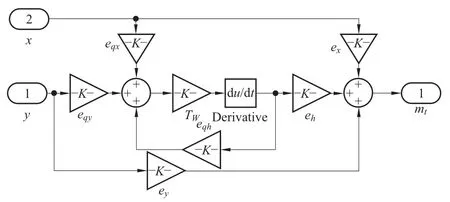
图5 线性水轮机仿真模型图
3.2 经典水轮机模型
如果假定水轮机理想无损,在额定工况点运行时,此时的传递系数eqy=1,eqx=0,eqh=0.5,ey=1,ex=-1,eh=1.5。则对于引水系统不太复杂的情况,一般可采用刚性水锤的表达式来描述其动态特性,因此建立引水系统和理想水轮机数学模型为:
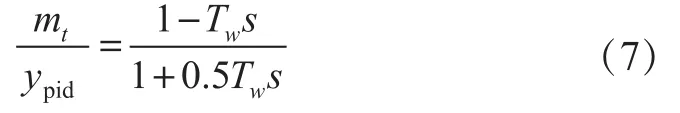
3.3 非线性水轮机模型一
根据公式(1),当机组工况剧烈变化时,传递函数不能被看做是常量,则水轮机特性可用积分形式力矩方程和流量方程表示为:
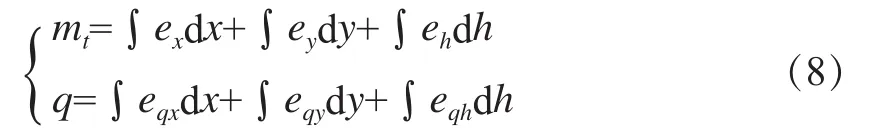
文献[5]以水轮机力矩特性为例,建立其Simulink仿真模型如图6所示。图中,自定义函数1=2.62/u^0.5,自定义函数2=u^0.5/Hr^0.5,x0=n0/nr,y0=a0/am,h0=H0/Hr,n0、a0、H0分别为稳态时的转速、导叶开度和水头。
依照以上做法,可以建立水轮机流量特性仿真模型,并于上面建立的刚性引水系统模型建立水轮机及引水模型,如图7所示。
3.4 非线性水轮机模型二
由IEEE Working Group提出的水轮机非线性数学模型综合考虑了水轮机导叶开度、水头、流量、机组负荷和外界扰动等因素,在大波动和小波动的情况下均可使用。则单机单管无调压井刚性水击下,非线性水轮机数学模型为:
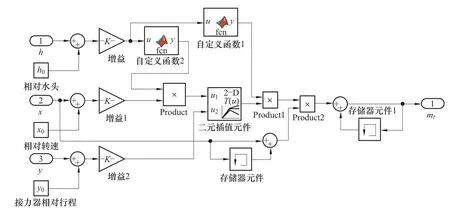
图6 水轮机力矩特性模型仿真图
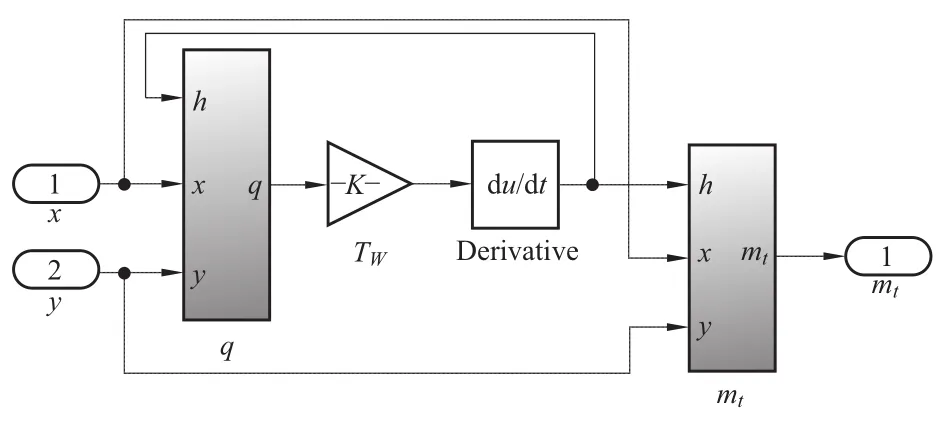
图7 非线性水轮机模型一仿真图

方程中各值均为相对值,其中qnl为空载流量相对值。则在Simulink环境下建立引水系统和非线性水轮机模型一如图8所示。
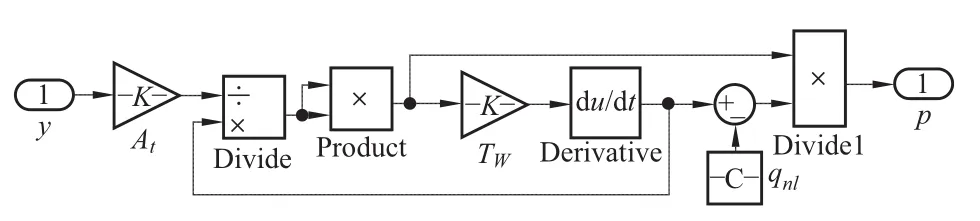
图8 非线性水轮机模型二仿真图
图8中At为理想导叶开度与实际导叶开度的比例常数,At=1/(YFL-YNL);YFL为水轮机最大导叶开度,YNL为水轮机空载导叶开度。
3.5 非线性水轮机模型三
曾云等人在模型二的基础上提出了弹性水击下水轮机出力的微分代数系统模型,并采用仿真方法,对水力系统非线性微分方程和其他传统计算方法进行对比,研究水轮机微分代数系统模型的计算准确性。研究结果表明,水轮机微分代数系统的可以较好地反映水轮机暂态过程的主要特征。非线性水轮机模型是由式(11)和式(12)构成的一个微分代数系统。详细的推导和验证过程见文献[6]。
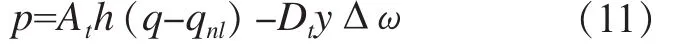
式中y是主接力器位移相对值;Dt为水力阻尼因子;∆ω为机组角速度偏差相对值。
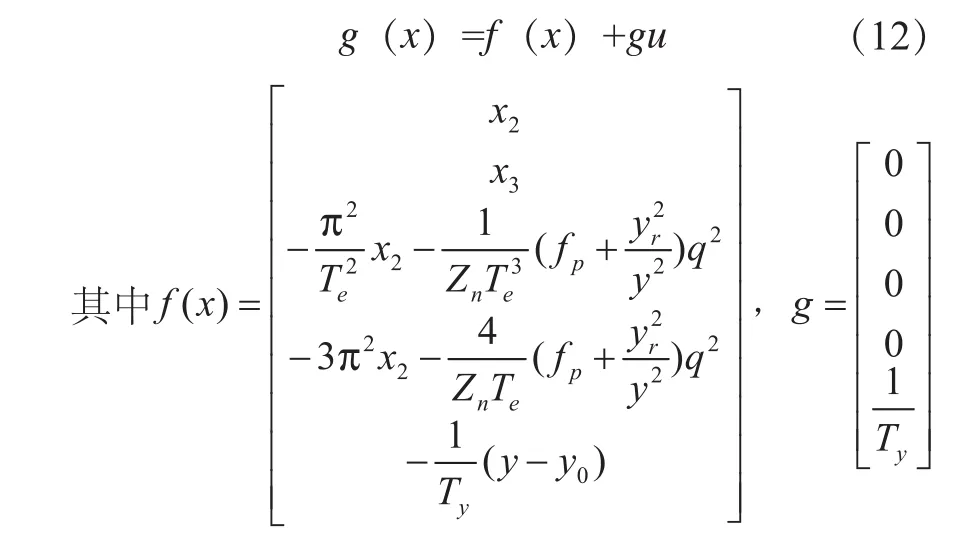
式中fp为引水系统水头损失参数;Zn为管道的水力浪涌阻抗的规格化值;Te弹性时间(s);Ty为主接力器时间常数(s);y0为主接力器初值相对值;yr为额定负荷时主接力器的位移相对值。水力系统传递函数为:
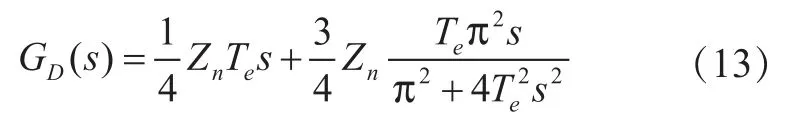
仿真中忽略了水力阻尼,取Dt=0,则采用Simulink建立非线性仿真模块如图9所示。
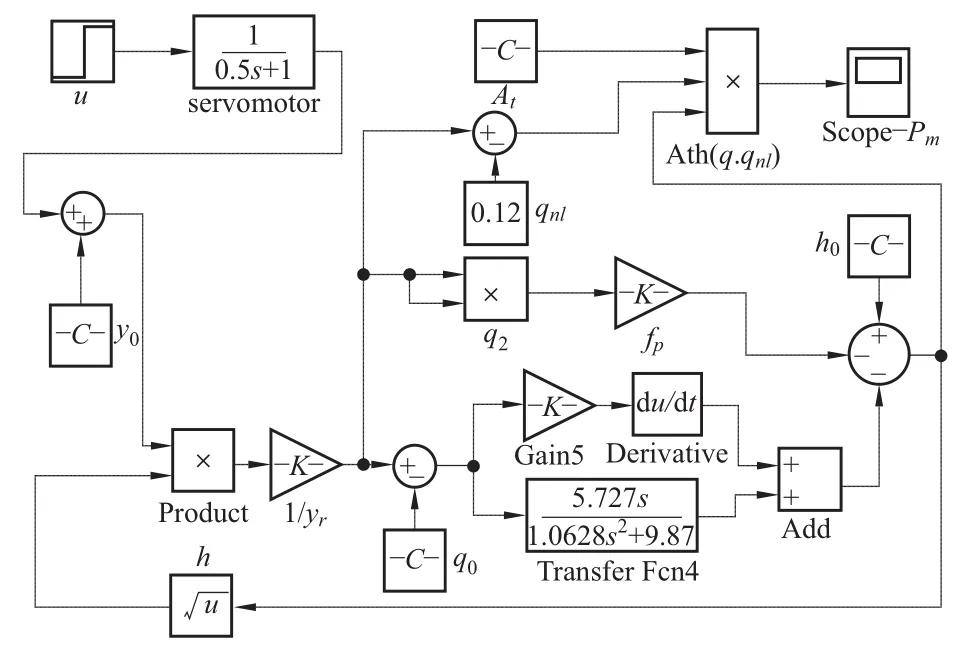
图9 非线性水轮机模型三仿真图
4 结束语
在扰动不大的情况下,选择水轮机线性模型就可以基本满足仿真要求,认为水轮机传递系数为常数。但当扰动剧烈时,水轮机的非线性不可忽略,选择非线性模型能更好地体现在波动下的调节过程。IEEE Working Group提出的系列模型,均忽略了尾水管真空部分的水头。对于中高水头水力机组,尾水管的水头所占比重较小,并且暂态过程中其变化相对值很小。忽略尾水管部分,对于研究机组暂态行为影响很小。否则,水轮机水头需要进行相应的修正[6]。曾云等人提出的弹性水击下水轮机出力的微分代数系统模型,采用了水利动态的微分方程形式,虽然存在一定的误差但验证结果较好。
针对不同水电站的实际情况,利用Simulink仿真系统强大的开放性和可移植性,可以根据相关的水轮机模型和调速器模型、引水系统模型、发电机及负荷模型结合起来,构建完整的水轮机调节系统仿真模型进行仿真计算。随着对非线性模型的研究进展,可以对复杂工况下的水电站调节系统进行仿真,相比较于在建模过程中忽略一些不必要因素的模型,更能体现实际的调节过程。但在实际应用过程中,还是要采用仿真与实际相结合的方法来进行设计研究。
[1] 魏守平.水轮机调节[M].武汉:华中科技大学出版社,1998.
[2] 罗旋,魏守平.基于MATLAB的水轮机调节系统仿真[J].水电站机电技术,2005,28(3):23~25,29.
[3] 袁璞.水轮机调节系统非线性建模及动力学分析[D].陕西:西北农林科技大学:5~8.
[4] 薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2006.
[5] 黄莉,李咸善,袁喜来.基于Simulink的水电机组模块化建模与仿真[J].水电自动化与大坝监测,2007,31(5):14~17.
[6] 曾云,张立翔,钱晶,徐天茂,郭亚昆.弹性水击水轮机微分代数模型的仿真[J].排灌机械工程学报,2014,(8).
[7] IEEE Working Group on Prime Mover and Energy Supply Models for System Dynamic Performance Studies,Hydraulic turbine and turbine control models for system dynamic studies,IEEE Trans. Power System,1992,7(2):167~179.
高 磊(1989—),男,硕士研究生,主要研究方向:水力机械自动化。E-mail: 286060705@qq.com
张成立(1966—),男,副教授,通信作者,主要研究方向:水力机组控制调节研究。E-mail: zhangchengli1118@163.com
秦正飞(1989—),男,硕士研究生,主要研究方向:水力机组故障诊断。E-mail: 1136397739@qq.com
汪 健(1990—),男,硕士研究生,主要研究方向:水力机组故障诊断。E-mail: 523669059@qq.com
Research on the Hydraulic Turbine Model in the Simulation of Hydro-Turbine Governing System Based on Simulink
GAO Lei,ZHANG Chengli,QIN Zhengfei,WANG Jian
(Faculty of Metallurgical and Energy Engineering,Kunming University of Science and Technology,Kunming 650093,China)
The hydro-turbine governing system established based on Matlab/Simulink platform which contributes to an understanding of the regulation process in the actual operation process. Hydro-turbine governing system is divided into four subsystems,includes the governor of hydraulic turbine,hydraulic system,hydraulic turbine and generator.This paper introduces the general forms of the system,and focuses on the summary and analysis of several hydraulic turbine models.
Simulink; simulation; hydro-turbine governing system; hydraulic turbine model; nonlinear model
