导体球面电像变换函数及其应用
2015-12-06刘国松李素文
刘国松,李素文
(长春工程学院,长春130012)
0 引言
电像法是英国物理学家开尔文勋爵首先提出的一种特殊方法,用于静电问题的求解。电像法的理论支撑是拉普拉斯方程、泊松方程在限定边界条件下的唯一性定理。该方法在应用过程中涉及点状原电荷在给定边界面下电像的个数、像电荷的位置和复杂带电体的像电荷形状、电荷分布两大类问题。作为电像法有效性的示例,接地无限大平面、无限长圆柱面、球面导体边界的点电荷电像计算于电磁场相关教科书[1-3],电像法的应用和讨论虽多有报道,因带电体和界面的复杂性带来的像电荷位置、电荷量的确定问题限制了电像法的应用范围,有时甚至需要依靠直觉加以判定。尽管如此,仍有很多成功的解析算例,如郑家奎[4]采用电像法处理了特殊角域静电场,这是有限电像;严雪飞[5]采用迭代电像法计算双导体球静电模型,并且讨论了多导体球问题,这是电像法应用的较为复杂又贴合实际的成功范例,其工作的重要性还在于将电像法应用于数值计算的预处理。
本文在导体球面边界条件下应用勒让德多项式与其母函数的关系,证明了引入导体球面电像的合理性和唯一性。引进电像变换函数用以表达导体球外带电体的像格林函数,以实现求解任意带电体电场中存在导体球界面情形下边值问题,最后给出了导体球一均匀带电圆环模型的数值算例。
1 球面电像的合理性、唯一性证明
对于导体球一点电荷静电模型,空间电势来源应有两部分(如图1):导体表面电荷σ和导体外的点电荷q。该情形下选取导体球心为坐标原点,球心与点电荷连线为球坐标系的南北连线。

图1 点电荷极化下的接地导体球电像模型
选取无穷远点为电势参考零点,则空间任意位置处的电势可以表达为

式中:r⇀′0为点电荷q的位置矢量,且其模为a;r⇀′为球面上任意点的位置矢量。
模型所满足的边值条件为

势函数具轴对称性,因而球面电荷对导体球外区域任意一点的电势贡献可以采用球对称球谐函数表达

因无穷远处为电势参考零点,故而Al=0,

将点电荷电势贡献用勒让德多项式展开[6]
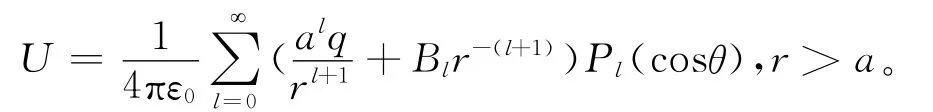
应用r=R处势函数须满足的边界条件

即得到对于l>0,

所以

所以

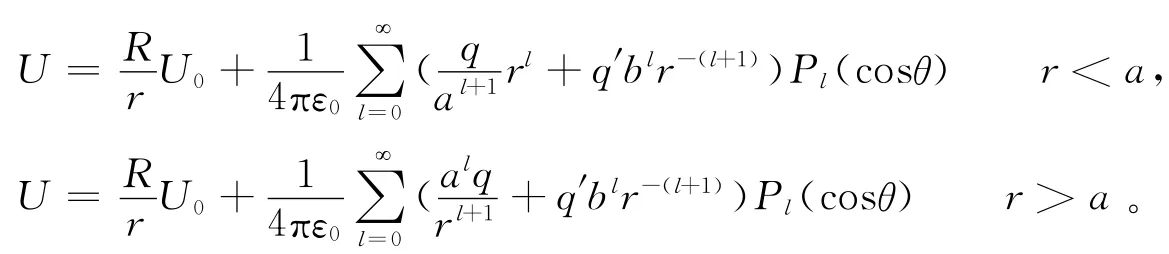

该式第一项表达球对称成分,是导体球表面均匀分布电荷的贡献,等效于某位于球心的点电荷电势;第三项为位于球内距球心b处,带电量为q′,且位于球心与点电荷q连线上的等效点电荷电势贡献。上述推证过程表明,导体球面边界下的点电荷镜像是严格的感应电荷等价描述,且具有唯一性。
2 导体球面电像变换函数
电荷的导体球面电像分析表明,对于任意的球外电荷分布下的任意点电荷微元dq(r′),对导体球外空间的电势贡献,都可以用该点电荷微元和像电荷微元的点元电势贡献表达,且像电荷位于原电荷位置矢径上,因而像电荷微元与原电荷微元的电量借助式(3)建立起唯一联系:

式中:dq(r′)表示原电荷微元;r′为原电荷微元位置矢量;dq′(r″)为像电荷微元;r″为像电荷位置矢量。且两者之间的位置变换关系为

则可以定义电荷变换函数及位置变换函数

位置变换函数实际上表达的是原、像格林函数关系。依据电像法的基本精神,应用静电场的可叠加原理,立即可以得到空间任意场点r的电势。

这实质上是在原电荷空间和像电荷空间分别进行的格林函数积分,若将电像变换函数代入,则


式(6)是仅在原电荷分布空间上的叠加积分。该式表明,引进电像变换函数,本质上把边值问题转化成了已知电荷分布下的直接电势叠加积分。
空间电场分布

我们感兴趣的还有导体球的表面电场强度,即电荷面密度的分布问题。显然
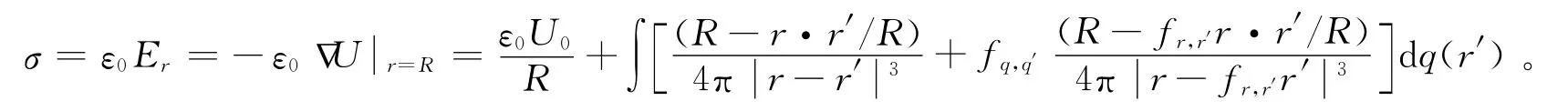
3 均匀带电圆环与接地导体球模型的数值解例
由于电荷变换和位置变换都是非线性变换,所以电势叠加积分通常不可解析求解。但是由于电像变换函数的引进,将给定边界条件下的数值计算简化为直接的数值积分,而数值积分在数值计算中是最为简单和成熟的技术,因而计算效益显而易见。
模型如图2所示,带电细圆环与导体球的某个子午面共面,电荷线密度为λ,半径与导体球相同,都为R,环心与球心相距3R。为简化数值模型,进行如下数值化预处理

图2中直接给出了带电圆环的电像。由于任意原电荷微元与导体球的间距均大于导体球半径,所以原电荷与像电荷无论电荷量还是线元长度都是缩小的,所以像带电体远小于原带电体,图示像环貌似圆环,实际上与圆环相去甚远,这缘于电像变换的非线性导致的线元形变。

图2 均匀带电圆环和接地导体球模型示意图
图2中像环的形状看似圆环只是与导体球和圆环相比尺寸太小而导致的视差。除此之外,像环上的电荷密度不再是均匀的。
依据电势叠加计算式(6)直接计算出空间电势分布函数,如图3所示。

图3 电势分布等高图式
彩色等高图式可以清楚地确定电势相对分布,粗略估量电场强度的分布状况。图中左侧圆环为导体球占据区,为零电势区。右侧红色区域为高电势区,且由于细圆环处电荷体密度发散导致电势函数发散。图中接近圆环线分布电荷的数据点进行了上截断处理。
4 结语
本文证明了导体球面电像的合理性和唯一性,引进电像变换函数,将边值问题直接转化为给定电荷分布下的电势叠加计算。并且给出了复杂原电荷分布、简单导体界面下的电势分布函数实际算例。
[1]Jackson J D.Classical Electrodynamics[M].Third Edition.Singapore:John Wiley &Sons,2001:57-64,86-87.
[2]俞允强.电动力学简明教程[M].北京:北京大学出版社,1999:56-61.
[3]虞福春,郑春开.电动力学[M].北京:北京大学出版社,1992:28-37.
[4]郑家奎.电像法求解角域静电场[J].泰山学院学报,2010,32(6):84-87.
[5]严雪飞.特殊的电像法研究多个导体球的相互作用[J].大学物理,2011,30(3):44-47.
[6]郭敦仁.数学物理方法[M].北京:高等教育出版社,1991:278-280.
