新里曼理论三和弦转换的基本模式及其扩展

2015-12-06高畅

音乐探索 2015年4期

关键词：倒影和弦移位

高畅

(四川音乐学院作曲系四川成都 610021)

新里曼理论三和弦转换的基本模式及其扩展

高畅

(四川音乐学院作曲系四川成都 610021)

新里曼理论著名的三种三和弦转换模式——P(平行转换)、L(导音转换)和R(关系转换)，是建立在上下关联倒影及声部进行极俭化(共同音最大化即保持两个共同音)基础上的。笔者首先对这三种基本模式进行了解读，进而在此基础上加以引申和扩展，对保持一个共同音的上下关联倒影和上下关联移位也作为三和弦的关联转换对待，从而提出了笔者的一些思考和设想。文中还对音网、转换网和转换图等诸多的与新里曼理论密切相关的概念以及新里曼分析中常见的表述方式进行了阐述。

新里曼理论；三和弦转换；关联倒影；关联移位；音网

新里曼理论(neo-Riemannian theory)①是自20世纪80年代开始在北美逐渐形成的，理查德·科恩(Richard Cohn)称它“源于大卫·列文(David Lewin)的三和弦关系转换的方法”②，业界也通常认为它是发端于列文的论文“A Formal Theory of Generalized Tonal Functions”③的。如果说80年代大卫·列文的一系列转换理论文献④中涉及到的与里曼功能理论相关的三和弦转换的一些论述是新里曼理论形成的根源或基础，那么90年代布莱恩·海尔(Brian Hyer)的包括“Reimag(in)ing Riemann”⑤等在内的诸多文献以及由约翰·克拉夫(John Clough)协同列文、科恩和杰克·杜塞特(Jack Douthett)等领衔的“布法罗工作组(Buffalo working group)”⑥通过召开一系列学术活动而取得的丰硕成果等则直接催生了新里曼理论这一学说的最终形成。从根源上来讲，新里曼理论的确是脱胎于或从属于大卫·列文创立的转换理论(transformation theory)的，因而业界普遍认为新里曼理论是通用转换理论的一个分支也就不足为怪了。不过，近三十年来，新里曼理论受热衷的程度大有盖过转换理论本身的趋势。不管怎样，在20世纪涌现出的以音高作为主要分析对象的分析理论中，新里曼理论的地位和影响在很大程度上都可以与申克分析理论、音级集合理论并驾齐驱，至少新里曼理论在不同程度上都对申克分析理论、音级集合理论形成了补充。

科恩认为，新里曼理论通常涉及到以下六个概念：三和弦转换(triadic transformation)、共同音最大化、声部进行极度节俭(parsimony)、“镜像”或“双重”倒影、等音等同和“音关系表(Table of Tonal Relation)”⑦。笔者以为，从某种程度上来讲，新里曼理论中这六个重要概念也可以理解为是新里曼理论所具有的普遍性特征，尽管新里曼理论标帜下的理论阐释并不一定都包含这六个概念或无须都具备这六个特征。也可以说，对上面六个概念或特征中的任何一个加以引申而作的理论阐述从某种程度上来讲都可以划归于新里曼理论的旗帜下。实际上，在上面六个概念或特征中，三和弦转换无疑是新里曼理论的核心内容，而等音等同既是非调性音乐的一个典型特征也是新里曼理论与里曼动能理论的一个明显不同点，至于包括“音网”(tonnetz)和“转换网”(transformation network)、“转换图”(transformation graph)等在内的“音关系表”，从本质上来讲只是一种表述方式而已。因此，六个概念或特征中的声部进行节俭化(涵盖了共同音最大化)和“镜像”或“双重”倒影无疑成为了新里曼理论的中心主题，甚至在很大程度上可以看作是新里曼理论构建的基础。概而言之，笔者以为，三和弦转换是新里曼理论的核心内容(但远远不是新里曼理论的全部，尤其从长远来看)，而上下关联倒影及声部进行的节俭则是新里曼理论赖以成立的根基，也是其标志性的特征。

新里曼理论尽管来源于胡果·里曼(Hugo Riemann，1849—1919)的功能理论的一些思想和原理，但是又不囿于和弦的调性功能关系，因此新里曼理论对于19世纪半音化的功能模糊的音乐的分析，以及20世纪的以三和弦为主要和声材料的音乐诸如一些简约派音乐甚至流行音乐的分析都有着广泛的应用。随着新里曼理论的持续发展，新里曼理论的三和弦转换原理已经延伸到了包括音高、集合、序列甚至时值等在内的各种元素之间的转换，因此，经过发展和延伸的新里曼理论似乎越来越脱离了其最初的面貌。也正因为如此，较广义的新里曼理论自然也广泛地应用于非调性音乐的分析中。这些，从《音乐理论杂志》(JournalofMusicTheory)专辟的“新里曼理论特刊”(1998，42/2)所辑录的文章就可略见一斑。另外，从相反的角度来看，新里曼理论的形成和发展又不同程度地唤起了人们对里曼理论的重新审视和重新评估。

毋庸置疑，新里曼理论自20世纪80年代于北美逐渐形成以来持续受到了众多学者的关注并取得了丰硕的研究成果，但就国内来说，至今却还是一个较为陌生的领域。在笔者写作此文时所能查阅到的国内期刊论文中，涉及到新里曼理论的可谓寥寥可数。其中，郭新教授的《自然音七和弦声部进行的转换》一文⑧涉及到了新里曼理论及其三和弦转换的一些背景知识，笔者在拙作《后调性理论中一些概念术语解析及中译名琐谈》⑨中也曾经简单地介绍了新里曼理论及其三和弦转换的概念。总的来说，这些文章的相关介绍都较为简略。

为此，本文拟对新里曼理论的三和弦转换的基本模式进行较为系统的解读，并在其基础上加以延伸，针对笔者所思考的建立在一个共同音关联这一基础上的上下关联倒影和上下关联移位的三和弦转换模式提出一些设想。文中还拟对音网、转换网和转换图等诸多的与新里曼理论密切相关的概念以及新里曼分析中常见的表述方式进行必要的阐述。

一、新里曼理论三和弦的表示方式

由于新里曼理论关注的是和弦之间的转换或运动而不是和弦之间的调性功能关系，因此我们以往习惯的功能标记(如T、S、D等)和建立在调性功能基础上的音级标记(如Ⅰ、Ⅳ、Ⅴ等)等方式在新里曼理论中都普遍不再采用了，取而代之的是下面将介绍的一些其他的方法。

在新里曼理论有关三和弦(大三和弦及小三和弦)的标记中，目前最普遍采用的是音名加“+”号或“-”号这样的方式，如“C+”表示C音为根音的大三和弦，而“E-”或“e-”则表示E音为根音的小三和弦，著名的新里曼理论家理查德·科恩普遍采用的就是这种方式⑩。当然，这样的标记方式是来源于大卫·列文的，他在有关三和弦转换的论述中，是用包含音高和符号的有序对(p，sign)来表示的，如C音为根音的大三和弦表示为(C，+)，E音为根音的小三和弦则表示为(E，-)。著名的新里曼理论家布莱恩·海尔也普遍采用这样的方式。

除了上面所述的用音名来表示的以外，还有用音级整数来表示的。譬如，在朱利安·胡克(Julian Hook)所用的非常数学化的表示方式即Δ=(γ,σ)中，Δ表示大三或小三和弦，γ表示模12的音级整数，σ则表示代表大三和弦的“+”或代表小三和弦的“-”，如Δ=(0,+)即表示根音为C音(pc0)的大三和弦，而Δ=(4,-)则表示根音为E(pc4)的小三和弦。

以上列举的仅仅是新里曼理论中较常见的表示三和弦的方式。可以说，新里曼理论中对于三和弦的表示方式还远远没有统一，而且，即便是同一位理论家，可能在不同的文本背景中也会采用不尽相同的表示法。

为了便于读者对上面所述的各种表示法都能够了解和熟悉，本文在后面的论述中将尽量变换不同的表示法。

二、新里曼理论三和弦转换的三种基本模式

里曼在他的功能和声理论的代表性著作《简明和声学》(VereinfachteHarmonielehre，1893)中阐述到，“特定的主、属或下属功能有三个基本的和弦变体：‘变形’(Variante)，它使具有相同根音的大、小三和弦(C大三和弦/C小三和弦)相互关联；‘平行’(Parallele)，它使相隔小三度的大、小三和弦(C大三和弦/A小三和弦)形成关联；‘导音转换’(Leittonwechsel)，它使相隔大三度的大、小三和弦(C大三和弦/E小三和弦)相互关联。”

新里曼理论中著名的三和弦转换的三种基本模式正是从里曼的三种“和弦变体”而来的，只不过除了导音转换在概念和含义上继续保持不变以外，里曼的“Variante”被译作并替换成了“Parallel”(平行)，而“Parallele”则被译作并替换成了“Relative”。大卫·列文将平行转换、导音转换和关系转换分别简称为PAR、LT和REL，也就是我们通常所简称的P、L和R。新里曼理论三和弦转换的最主要特征被普遍认为是：“上下关联倒影”(contextual inversion)及声部进行的极度节俭(voice-leading parsimony)或共同音最大化(含两个共同音)。也就是说，新里曼理论著名的P、L和R这三种转换方式都具有这样的特征：转换的和弦之间为倒影的关系，即大三和弦转换为小三和弦或小三和弦转换为大三和弦，而且转换的两个三和弦之间的共同音是最大化的，即含有两个共同音。实际上，新里曼理论中出现频率最高的“上下关联倒影”这一概念，往往都蕴含了前面所述的全部特征。当然，我们也可以说，三和弦转换一般是指倒影等同且共同音最大化的三和弦之间的变换。

下面对新里曼理论三和弦转换的三种基本模式作一个简要的概括：

(一)平行转换

(二)导音转换

(三)关系转换

谱例1 以大三和弦C—E—G为例的三和弦转换的三种基本模式

三、三和弦转换的扩展模式

本文在新里曼理论三和弦转换三种基本模式的基础上加以延伸，将保持一个共同音的上下关联倒影和上下关联移位也作为关联转换来对待。

(一)保持一个共同音的关联倒影转换

当大三和弦或小三和弦以保持一个共同音这样的关联而倒影时，则可以构成倒影等同但共同音仅为一个的转换。约瑟夫·N.斯特劳斯(Joseph N.Straus)在《后调性理论导读》(IntroductiontoPost-TonalTheory)一书中可能是由于引入了大卫·列文的SLIDE转换的缘故，故而将围绕着三和弦的一个音的倒影也作为上下关联倒影来看待。

保持一个共同音的关联倒影转换也有三种方式，现分别概述如下：

1.平行倒置转换

2.导音倒置转换

3.关系倒置转换

谱例2 以大三和弦C—E—G为例的保持一个共同音的三种关联倒影转换方式

4.P′/L′/R′转换与P/L/R转换的关联和区别

为了便于理解和记忆，我们下面以“源(source)”——大三和弦C+为例，来比较一下其P和P′、L和L′以及R和R′的一些关联和区别，见例3。

谱例3 三种基本转换模式与其倒置转换的关联和比较

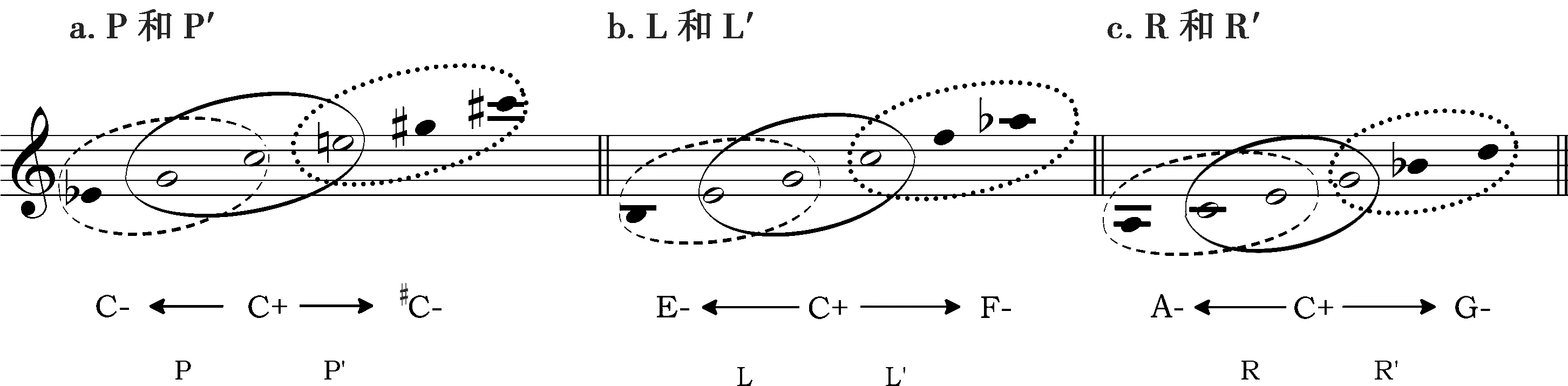
当“源”——大三和弦作密集的四六和弦排列时，其P转换是以下方两个音(纯四度排列的五音和根音)为轴的倒影转换，而其L′转换则是以其余的一个音(即三音)为轴的倒影转换，见例3a。当“源”——大三和弦作密集的六和弦排列时，其L转换是以下方两个音(小三度排列的三音和五音)为轴的倒影转换，而其L′转换则是以剩余的一个音(即根音)为轴的倒影转换，见例3b。当“源”——大三和弦作密集的原位排列时，其R转换是以下方两个音(大三度排列的根音和三音)为轴的倒影转换，而其R′转换则是以剩余的一个音(即五音)为轴的倒影转换，见例3c。

对于“源”为小三和弦的P和P′、L和L′以及R和R′的关联和区别，与上面所述相类似，此处不再赘述。

另外，保持一个共同音的三种倒影转换方式都可以由P、L和R的不同复合操作而构成。例4中例举的仅仅是其中可能的一些复合操作模式。

谱例4 P′、L′和R′转换可由P、L和R的不同复合操作而构成

尽管P′、L′和R′都可以理解为是由P、L和R的不同组合而构成的复合操作，但在某些特定的语境中，为了分析和表述的方便，我们也常常将P′、L′和R′作为特定的转换方式来看待。

(二)保持一个共同音的移位转换

按照克拉姆彭豪尔(Klumpenhouwer)的表述，里曼除了“Wechsel”(转换，exchange)即大、小三和弦之间的转换以外，还确立了“Schritt”(阶移，step)这种大三和弦之间或小三和弦之间的和弦关系或和弦转换方式。实际上，新里曼理论的一些文献中也常常将“Schritt”(阶移)看作是一种或一类和弦转换方式。布莱恩·海尔就曾将里曼的“二元建构”(dual construction)看成是由四种和弦转换方式呈代数交互作用而形成的一种结构，其中的四种转换除了平行转换、导音转换和关系转换外，还包括了属(dominant)转换。另外，大卫·列文在论述转换理论时也涉及到了“属转换”，他用“DOM”来表示，如C+到F+的转换即为属转换，其表达式为(C，+)DOM=(F，+)，而F+到C+的下属转换，由于其为属转换的逆转(reverse)，因此列文将其表示为(F，+)DOM′=(C，+)或(F，+)DOM-1=(C，+)。

笔者在海尔所表述的属转换以及大卫·列文所定义的“DOM”和“DOM′”转换的基础上加以扩展，将凡是含有共同音的大三和弦之间或小三和弦之间的上下关联的移位(contextual transposition)也列为广义的关联“转换”之列。实际上，这并不完全是笔者的主观臆想。仅就笔者所掌握的资料来看，至少在约翰·克拉夫1998年的论文中就明确出现了“上下关联移位”这一术语。如果按照该文中所提到的“里曼—克拉姆彭豪尔‘阶移和转换’群组”(Riemann-KlumpenhouwerSchritt/Wechselgroup，缩写为S/W)来看待，那么音级空间中的24个大小三和弦则相当于是集合族3—11(037)的12个移位成员和12个倒影成员而构成的“T/Igroup”(即移位和倒影群组)。当然，本文所阐述的内容和角度是与其不完全相同的，本文所述的上下关联移位转换是特指有共同音相关联的。

对于大三和弦或小三和弦而言，“移位等同”的三和弦之间最多只有一个共同音，这从集合理论中“移位中的共同音”的相关知识以及集合族3—11(037)的音程向量001110中就可以很容易地领会到。

1.大三和弦的移位转换

对于大三和弦的移位转换，我们以大三和弦[C,E,G]为例，其移位等同且含有一个共同音的转换方式如例5所示。

谱例5 大三和弦[C,E,G]的单向的移位转换

对于例5所列举的移位转换方式，如果抛开调性功能中和弦之间的倾向性而仅从转换的角度来看，D转换应该指从主和弦到属和弦的转换才似乎更容易理解一些，按大卫·列文的表示方法则应该为(C,+)(D)=(G,+)，海尔也曾经作过这样的表述。相应地，例5中M转换和SM转换似乎也应该分别看作是主大三和弦到中音大三和弦和主大三和弦到下中音大三和弦的转换才更容易理解一些。但是，本文最终采用了布莱恩·海尔所最终采取的方式，即为了新里曼理论在表述和标记方面的统一，一律遵循大卫·列文的定义，统一将从属和弦到主和弦的转换称为D转换，相应地，从上中音大三和弦和下中音大三和弦到主大三和弦的转换分别称为M转换和SM转换。当然，本文的M转换和SM转换在和弦结构方面是与列文的建立在调性功能内的MED转换和SMED转换不同的。另外，对于例5中的M转换和M′转换，理查德·科恩则是直接将其标记为PL和LP。

概而言之，对于例5中从大三和弦出发的保持一个共同音的六种移位转换，D转换相当于属和弦到主和弦的转换，即列文定义的DOM；D′相当于下属和弦到主和弦的转换，即列文定义的SUBD(或D′或DOM-1)；M相当于上中音上的与主和弦同结构的大三和弦到主大三和弦的转换，此为非调性功能背景下的，故在和弦结构方面是与列文在调性背景中定义的“MED”不同的；M′可理解为M的倒转；SM可理解为下中音上的与主和弦同结构的大三和弦到主大三和弦的转换，这同样与列文的调性背景中的“SUBM”转换在和弦结构方面也是不同的；SM′则可理解为SM的倒转。

如果采用音级集合的方式，那么大三和弦的移位转换则可以表述为：对于任何一个根音为x(模12整数)的大三和弦，其D转换(结果)为Tx+5，D′转换为Tx+7，M转换为Tx+8，M′转换为Tx+4，SM转换为Tx+3，SM′转换为Tx+9。

2.小三和弦的移位转换

从例6可以看出，在小三和弦的移位转换中，D转换相当于属和弦到主和弦的转换，D′相当于下属和弦到主和弦的转换，这两种转换从本质上来讲也是与列文的定义相同的。但是，例中的M转换和SM以及M′和SM′转换则在和弦结构方面也是与列文不同的，这里的M转换相当于上中音上的与主和弦同结构的小三和弦到主小三和弦的转换，M′可理解为M的倒转,SM相当于下中音上的与主和弦同结构的小三和弦到主小三和弦的转换，SM′则可理解为SM的倒转。

如果用音级集合的方式来对小三和弦的移位转换进行表述，那么则为：对于任何一个根音为x(模12整数)的小三和弦，其D转换(结果)为Tx+5，D′转换为Tx+7，M转换Tx+9，M′转换为Tx+3，SM转换为Tx+4，SM′转换为Tx+8。

对比例6和例5，我们可以看出，小三和弦的D和D′转换相应的复合操作LR和RL与大三和弦的D和D′转换相应的复合操作RL和LR相比是互为逆向的，小三和弦的M和M′转换相应的复合操作PR和RP与大三和弦SM′和SM转换相应的复合操作RP和PR相比是互为逆向的,小三和弦的SM和SM′转换相应的复合操作PL和LP与大三和弦M′和M转换相应的复合操作LP和PL相比是互为逆向的。

3.三和弦移位转换的其他表示方式

不管是大三和弦的移位转换还是小三和弦的移位转换，其六种移位转换方式也可以用通用的集合方式来表述。我们既可以简单地将其表述为：对于任何一个大三和弦或小三和弦[x,y,z](标准型排列)，其D转换(结果)为Tx-z，D′转换为Tz-x，M转换为Tx-y，M′转换为Ty-x，SM转换为Tz-y，SM′转换为Ty-z。另外，我们也可以将其更详细地表述如下(表1)：

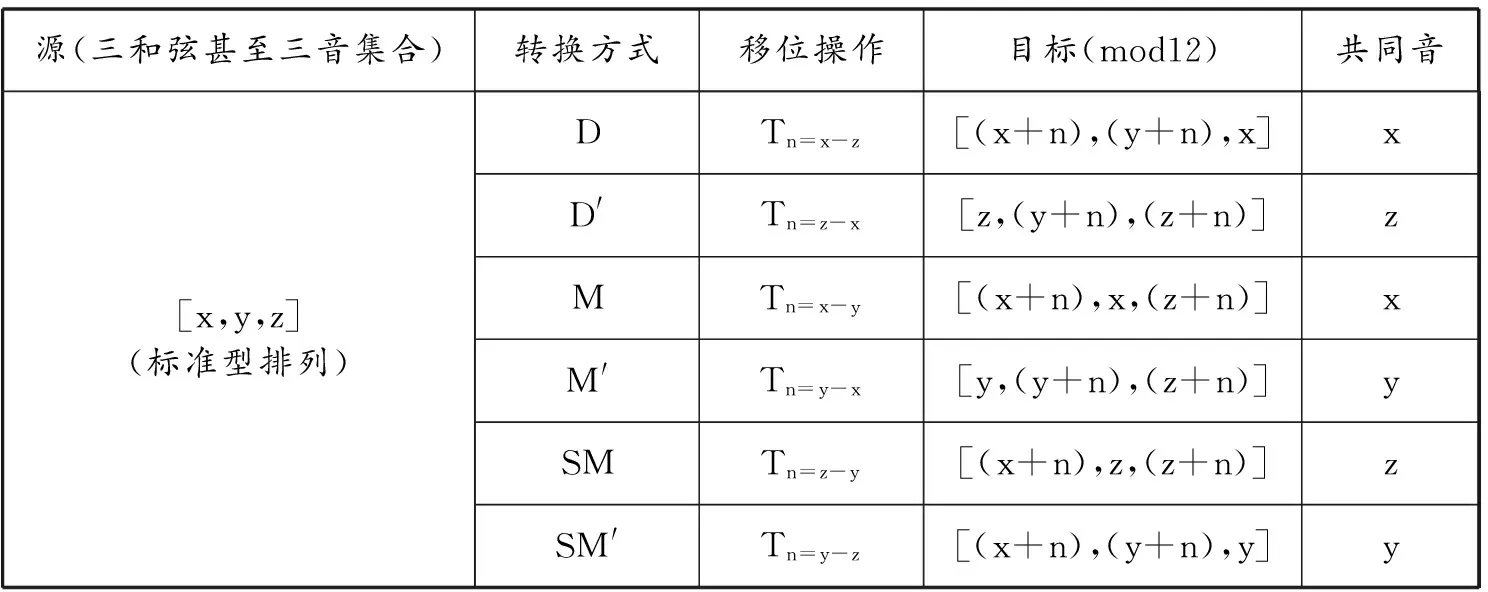
源(三和弦甚至三音集合)转换方式移位操作目标(mod12)共同音[x,y,z](标准型排列)DTn=x-z[(x+n),(y+n),x]xD'Tn=z-x[z,(y+n),(z+n)]zMTn=x-y[(x+n),x,(z+n)]xM'Tn=y-x[y,(y+n),(z+n)]ySMTn=z-y[(x+n),z,(z+n)]zSM'Tn=y-z[(x+n),(y+n),y]y

表1从[x,y,z]出发的移位转换

当然，表1中移位转换的集合表述方式，除了对大三和弦的移位转换或小三和弦的移位转换都是适用的以外，对于其他所有三音集合的上下关联的移位转换也是适用的。

另外，如果我们从“一元论”的角度和在非调性的语境中来看，不管是大三和弦的移位转换还是小三和弦的移位转换，由于D和D′在转换方式上是互为逆转的(reversed)，因此某些时候我们也可以将它们划归为同一种转换，这与卡罗尔·克卢汉斯(Carol Krumhansl)的表述是一致的。同理，M和M′某些时候也可以划归为同一种转换，而SM和SM′也可以划归为同一种转换。也就是说，上述的六种单向的转换在某些时候也可以用下面的三种双向的转换方式来进行概括，见例7。

谱例7 双向的移位转换

但是，由于集合理论中的移位通常是有向的或单向的，因此为了与音级集合理论相统一，我们一般情况下还是将单向的六种移位转换方式来分别进行对待。

四、三和弦转换的音网表示法

著名的里曼音网(RiemannTonnetz)或厄廷根—里曼音网(Oettingen-RiemannTonnetz)是一种抽象地表示音高之间以及和弦之间、调性之间关系的两维(two-dimensional)图表，新里曼理论自然也继承了这种方式，并已经扩展到了三维甚至四维的空间形式。尽管音网从本质上来讲只是一种普遍用于表述音高关系的方式，但它也成为了新里曼理论家们所热衷研究的一个领域。当然，这些理论家们的研究，有的已经超出了三和弦以及七和弦的范畴，有的则是把音网作为一种表述转换方式或转换模式的方式来对待了。

前面曾谈到，理查德·科恩把“音关系表”(主要指音网)看作是新里曼理论所包含的一个概念。笔者认为，音网的运用某种程度上可以看作是新里曼理论的一个普遍性特征，尽管它不是一个本质的或必须的特征。一个普遍的事实是，音网表示法在新里曼理论的阐述中有着极为广泛的运用。

对于本文前面所述的三和弦转换的十二种方式(包括基本的和扩展的)，如果用音网的方式来进行表述，那么则可以表示如下：

a.大三和弦[C,E,G]为基点

b.小三和弦[C,E,G]为基点

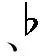
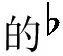
五、单一转换和多重复合转换

从集合的角度来看，任何一个三和弦与其他24个三和弦(包括该和弦本身)的进行，都可以用移位或倒影移位的方式来表示。朱利安·胡克把从任何一个三和弦到其它24个三和弦(包括该和弦本身)的转换称为“统一的三和弦转换(uniform triadic transformation)”，简称为UTT。对于24个UTT，胡克用<+,n,(12-n)>和<-,n,(12-n)>这样的方式来表示，其中第一个元素“+”表示大三和弦之间的转换或小三和弦之间的转换，“-”则表示大三和弦与小三和弦之间的转换或小三和弦与大三和弦之间的转换，第二个元素n为大三和弦转换到其他大三和弦或小三和弦的根音之间的半音数之差(有序音级音程)，第三个元素(12-n)则为小三和弦转换到其他小三和弦或大三和弦的根音之间的半音数之差。譬如，<+,1,11>概指C+D+和C-→B-，以C+→D+和C-→C-等；<-,10,2>则概指C+B-和C-→D+，以及D+→C-和D-→E+等。

不过，本文所讨论的单一的转换模式(包括三种基本转换模式以及九种扩展模式)，都是在共同音关联这一前提条件下的。对于没有共同音关联的三和弦的进行或转换，除了胡克的UTT表示法以外，还均可以用三种基本转换方式的多重的复合操作(compound operation)来理解，如[C,E,G]到[D,F,A]的转换路径可以为RLR，而[C,E,G]到D,F,A]的转换路径则可以为PLRL，等等。当然，如果将本文所阐述的九种扩展模式也作为单一的转换方式来看待，那么没有共同音关联的和弦之间的连接也可以按扩展模式的复合操作或扩展模式与基本模式的复合操作来理解。如C+→B+，尽管有多种的复合操作的理解方式，但在某种语境中我们可以将其理解为是L和L′的复合操作。

科恩将PLR操作笼统地作为一个家族或系列来看待，将其定义为PLR系(PLR-family)，其单一的操作如

、和均构成大三和弦与小三和弦之间的倒影转换，而二重操作如、、、、和则构成同一性质的大三和弦之间或者小三和弦之间的移位转换。三重操作如等则又退回到与单一操作模式相当的大三和弦与小三和弦之间的倒影转换，四重操作如等则又退回到与二重操作模式相当的同一性质的大三和弦之间或者小三和弦之间的移位转换。其余更多重的复合操作则以此类推。

从某一源(source)出发的复合操作，其路径通常是单向的或有向的。也就是说，对于同一源，通过由复合操作构成的路径而到达的目标，与该路径逆向而到达的目标尽管有时是相同的，如[0,4,7]=[1,4,8]且[0,4,7]=[1,4,8]，见图2a，但在很多时候则是不相同的，如[0,4,7]=[5,9,0]而[0,4,7]=[7,11,2]，见图2b。

a.“源相同/路径互为逆行/目标相同”的示例

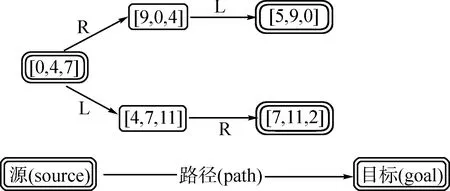
b.“源相同/路径互为逆行/目标不同”的示例

六、新里曼分析及其常见的表述方式

尽管三和弦常常被认为是调性音乐的一种基本元素，但新里曼理论的三和弦转换常常又不受调性逻辑的束缚，因此以三和弦转换作为其核心内容的新里曼理论一方面广泛地应用于19世纪的调性极度扩张的半音化的音乐的分析中(如理查德·科恩等对舒伯特、勃拉姆斯、布鲁克纳、理查·斯特劳斯、瓦格纳等作曲家的作品的分析)，当然也广泛地应用于20世纪的使用三和弦元素的音乐作品的分析中(如约瑟夫·N.斯特劳斯在《后调性理论导读》一书中就广泛地应用于使用三和弦元素的后调性音乐的分析中)。

下面仅对新里曼分析(neo-Riemannian analysis)中常见的三和弦转换的表述方式作一个简要的介绍。

(一)对三和弦及其转换模式进行标注的方式

在新里曼分析中，最常见的一种表述方式是直接对和弦及其转换模式进行标注，这与传统的调性和声分析中标注调性、和弦及和声进行的方式相似，如例8所示。

谱例8 理查·斯特劳斯：《春天》(自《最后的四首歌》)，第1—4小节

当然，在新里曼分析中，也常常将作品缩写或还原为“和声图式”，然后再作新里曼式的各种标注。例9显示是的来自列文对瓦格纳作品片断的分析图式，即为这样的方式。

谱例9 瓦格纳：《帕西法尔》，第三幕，第1098—1102小节

(二)音网模型方式

音网除了常用来表述音之间的抽象关系(正如前面所述的那样)以外，也可以用于分析作品时表述和弦之间的转换关系或进行方式。例10来自理查德·科恩对贝多芬作品片段所作的分析，其中a近似于我们所熟悉的“和声图式”那样的缩谱，b则为该作品片段的音网模型(tonnetz model)。

谱例10 贝多芬：《F大调小提琴和钢琴奏鸣曲》(第五号，“春天”)OP.24，第二乐章，第38—54小节

a.“和声图式”

b.音网模型

这样的“音网模型”表示方式在科恩的著作AudaciousEuphony：ChromaticHarmonyandtheTriad’sSecondNature中有着极为广泛的运用。

(三)转换网和转换图

转换网(transformation network)和转换图(transformation graph)是大卫·列文的通用的转换理论分析中极为常见的表述方式，自然在其所谓的分支理论——新里曼理论的分析中也有着广泛的应用。

下面的“图3”来自列文，图中显示的是贝多芬《热情奏鸣曲》第二乐章开头片断的三和弦转换网，也就是列文在文中所指的“发音体网”(network of Klangs)。

图3 列文概括的贝多芬《热情奏鸣曲》第二乐章第1—5小节的三和弦转换网

图中的“INDENT”表示等同性，“SUBD”表示下属转换，“REL”表示关系转换，“PAR”表示平行转换，“DOM”则表示属转换。

需要注意的是，一般地，转换网(transformation network)中的节点(node)通常都是具体而明确的，而转换图(transformation graph)中的节点则通常是“空的”，也可以说是不具体的，它既可以概指音高或音级，也可以概指音高或音级构成的序列，甚至本身就可以是一个网(network)等等。也就是说，转换网通常是具体而明确的，而转换图则通常是抽象而概括的。

以上略举的仅仅是新里曼分析中最常见的三和弦转换的表述方式。实际上，新里曼分析的表述方式是极为多样的，其中包括了各式各样的数学(包括几何、代数等)表示方式。这些，从某种程度上来说也是新里曼理论以及新里曼分析的一大特点。

结语

由于新里曼理论所涵盖的内容是极为庞杂的，因此，尽管本文原本只是计划对新里曼理论作一个稍微全面而系统的介绍并就一些相关的概念和原理谈一些笔者的思考而已，结果篇幅却大大超出了笔者原先的意料，故而只好将本想纳入本文的三和弦的PLR循环、RICH(倒影移位链)和TCH(移位链)操作等内容割舍了(待另文论述)。

纵览本文所阐述的内容，可以概括为以下两个部分来对待：

第一个部分是对新里曼理论及其三和弦转换的三种基本模式、音网等基本概念和原理进行介绍的。虽说是介绍，但其难度也远远超出了笔者原先的想象。究其原因有二：其一，尽管新里曼理论自上世纪80年代在北美形成以来一直受到了音乐理论界持续不断的关注且取得了非常丰硕的研究成果，但业界对新里曼理论及其众多的相关概念和原理的界定至今尚不十分明确，对相关的表示方式也没有完全形成统一；其二，此部分内容所涉及的相关概念和术语也是极为庞杂的(这从本文的注释就可略见一斑)。因此，对于此部分内容的解读，在不同程度上都包含了笔者的个人理解和思考。

第二个部分则是对保持一个共同音的上下关联倒影和上下关联移位的转换方式的思考和系统论述，这在很大程度上都可以算作是笔者的大胆设想。对于此部分的内容，尽管很多理论家都或多或少涉及过，但笔者至今还未见到系统而全面的论述，因此该部分内容的论述则更是贯穿了笔者的思考和个人观点。

基于上面所述，文中若出现不妥之处恐在所难免。为此，笔者在祈望读者能够理解并给予佐证的同时，更希望本文能引起国内音乐理论界对新里曼理论的进一步关注和认识，这既是本文的最终目标，也是笔者所希冀的本文的最大价值所在了。

诚然，随着新里曼理论研究的持续和不断深入，除了其中的很多领域尚待人们继续探究以外，对其价值进行客观的评价也是一个尚待深入探讨的问题。比如，新里曼理论常常将声部进行的节俭看作是其理论构建的一个基础，但面对实际的音乐文本，声部进行并不总是按这样的理论化模式而体现出来的，因此新里曼理论及其目前所运用的各式各样的表述方式是否能真正揭示音乐运动的本质？诸如此类的问题尚待我们进一步进行思考和研究。但是，不管怎样，新里曼理论及其各种表述方式毕竟为我们分析音乐作品提供了一些新的视角和新的分析手段，故而对其进行系统的介绍和研究无疑是极为必要的。

注释:

①大卫·列文(David Lewin)也曾将其称为后里曼转换(post-Riemannian transformation)理论，见David Lewin，MusicalFormandTransformation，Oxford：Oxford University Press，2007，p.xiii.

②Richard Cohn，“Introduction to Neo-Riemannian Theory：A Survey and A Historical Perspective”，JournalofMusicTheory，1998，42/2，p.170.

③David Lewin，“A Formal Theory of Generalized Tonal Functions”，JournalofMusicTheory，1982，26/1，pp.23-60.

④较重要和代表性的文献有：David Lewin，“A Formal Theory of Generalized Tonal Functions”，JournalofMusicTheory，1982，26/1，pp.23-60；GeneralizedMusicalIntervalsandTransformations，New Haven:Yale University Press，1987.etc.

⑤Brian Hyer，“Reimag(in)ing Riemann”，JournalofMusicTheory，1995，39/1，pp.101-138.

⑥Edward Gollin and Alexander Rehding eds.，TheOxfordHandbookofNeo-RiemannianMusicTheories，Oxford：Oxford University Press，2011，p.ⅸ.

⑦同注②，p.169.

⑧郭新：《自然音七和弦声部进行的转换——用新黎曼主义理论的观点分析流行音乐中的和声进行》，《黄钟》，2004年第4期，第26—34页。

⑨高畅：《后调性理论中一些概念术语解析及中译名琐谈——翻译斯特劳斯〈后调性理论导读〉一书后的思考》，《音乐时空》，2013年第12期，第41—44页。