抗强剪切攻击的四元数彩色图像零水印算法
2015-12-06何冰
何 冰
(1. 渭南师范学院物理与电气工程学院,陕西 渭南 714099;2. 陕西省X射线检测与应用研究开发中心,陕西 渭南 714099)
抗强剪切攻击的四元数彩色图像零水印算法
何冰1,2
(1. 渭南师范学院物理与电气工程学院,陕西 渭南 714099;2. 陕西省X射线检测与应用研究开发中心,陕西 渭南 714099)
针对现有彩色图像零水印算法对存在信息量丢失的各种攻击(如剪切、行列移除、涂抹等)的不足,提出一种基于非负矩阵分解(NMF)和四元数实矩阵的彩色图像零水印算法。该算法首先提取彩色图像的3个分量(R、G、B)并将各分量进行NMF分解;其次将分解后的各系数矩阵在版权中心进行注册,同时将原始彩色图像使用四元数实矩阵来表征,并计算实数字矩阵的Krawtchouk不变矩;最后,在版权中心注册Krawtchouk不变矩特征向量;由剩余未剪切部分的彩色图像和注册的系数矩阵共同恢复出完整的原始图像。实验结果表明:在彩色图像剪切或涂抹面积超过80%时,水印信息仍可以正确地被提取;使用四元数彩色图像整体法表征图像在图像类聚以及水印误检率方面的性能都要优于彩色图像三通道分别处理或直接灰度化实现的效果。
四元数;零水印;彩色图像;不变矩;非负矩阵分解
零水印技术因其很好解决了传统水印技术中不可见性和鲁棒性之间的矛盾,近几年来在信息安全领域中成为研究的热点。温泉等[1]在2003年首次提出零水印的概念,同时利用高阶累计量构造零水印特征,通过仿真实验证明所提出算法的有效性和实用性。此后零水印方面相关的文献和学术成果不断增多[2-4],马建糊和何甲兴[5]提出了一种基于小波变换的零水印算法,该算法利用一次小波变换后的低频系数与二值水印图像相异或运算来构造零水印信息,并将其在可信第三方(certificate authority,CA)中心进行注册;陈伟琦和李倩[6]采用双零水印嵌入方式,同时利用(singular value dfecomposition,SVD)空间向量来表征图像的算法,解决了目前零水印算法虚警率高的问题;张春凯等[7]设计了一种基于 Krawtchouk矩和NSCT(non-subsampled contourlet transform)变换的鲁棒性零水印算法,对图像进行 NSCT分解后,计算其低频成分的Krawtchouk低阶矩不变量来构造特征向量,并仿真实验来证明算法的有效性;冯银波和陈善学[8]将彩色图像在四元数域内分别进行分块离散傅里叶变换、分块离散余弦变换以及奇异值分解之后产生两组二值序列,将二值序列与版权标志信息相结合构造零水印信息,实验结果表明,所设计的算法对常规攻击以及部分组合攻击具有较强的鲁棒性。吴伟民等[9]利用细胞自动机变换将图像分离成低频子带和高频子带,然后对低频子带图像分块后进行奇异值分解,最后利用分解后的奇异值矩阵零水印信息的设计。
以上零水印算法对于常规的信号处理(如:滤波、JPEG有损压缩、一般的几何变换等)具有一定的有效性,而对于信息量受损或丢失的信号处理(如:剪切、涂抹、行列移除)的研究国内相关文献报道还比较少。文献[10]提出一种根据人类视觉模型,使用混沌系统及提升小波变换的抵抗剪切攻击的彩色图像盲数字水印算法,实验结果证明在抗剪切方面的性能较为显著;文献[11]提出一种基于 Radon变换不变矩和小波提升的水印算法,实验结果证明对几何变换具有很好的鲁棒性;文献[12]提出一种扩频水印算法,该算法在水印嵌入前,先对水印图像进行面包师变换,使得水印图像的像素能够均匀分布于每个区域,由此获得了一组具有可以抵抗剪切攻击能力的水印序列。文献[13]利用Patchwork方法同时结合相应的量化索引调制,提出一种抗剪切攻击的数字水印方法,该方法对剪切及压缩、噪声等图像处理具有良好的效果。文献[10-13]所提出的水印算法,在抗剪切攻击方面的性能均得到了一定的提高和改善;然而这三种算法都具有相同的不足之处:①随着水印嵌入数据量的增加,嵌入水印后的图像其不可感知性随之下降,即水印的鲁棒性和不可见性之间的矛盾是传统水印算法均需要解决的问题;②这 3种算法对于图像信息量损失或丢失百分比在 50%以下的剪切攻击,水印检测器可以正确地提取出完整的水印信息,但对于某些强剪切攻击(图像信息量丢失百分比超过75%),均无法正确地提取出原始水印信息。近几年来,相关学者将非负矩阵分解(nonnegative matrix factorization,NMF)应用到图像处理、图像识别领域。文献[14]提出一种基于 NMF的谱聚类集成(synthetic aperture radar,SAR)图像分割算法,使用NMF方法合并相关图像分割后的个体,实验结果表明,该方法优于 K-means方法、基于 Nystrom逼近的方法和Meta-clustering方法,具有一定的实用性。虽然NMF[15-16]在图像处理方面有一定的应用,但将其应用到零水印算法中的相关文献鲜见报道[17-18]。
通过以上分析,本文提出一种基于NMF和四元数实矩阵的彩色图像零水印算法。该算法根据NMF部分感知全局的特性,利用剪切后剩余部分图像及之前保存过的相应系数矩阵可以重构出完整的原始图像,解决了强剪切带来的问题;同时引入四元数理论,将其应用到彩色图像中,由于彩色图像3个通道(R、G、B)之间存在着非常紧密的光谱联系,若将彩色图像每一像素点处作为一个完整的体系来处理,那么每个像素点三个通道间的光谱联系就会贯穿在整个图像的运算和处理之中,本文使用四元数实矩阵来表征彩色图像,通过对零水印算法的设计,有效地提高了水印在提取阶段的检测精度。
1 非负矩阵分解
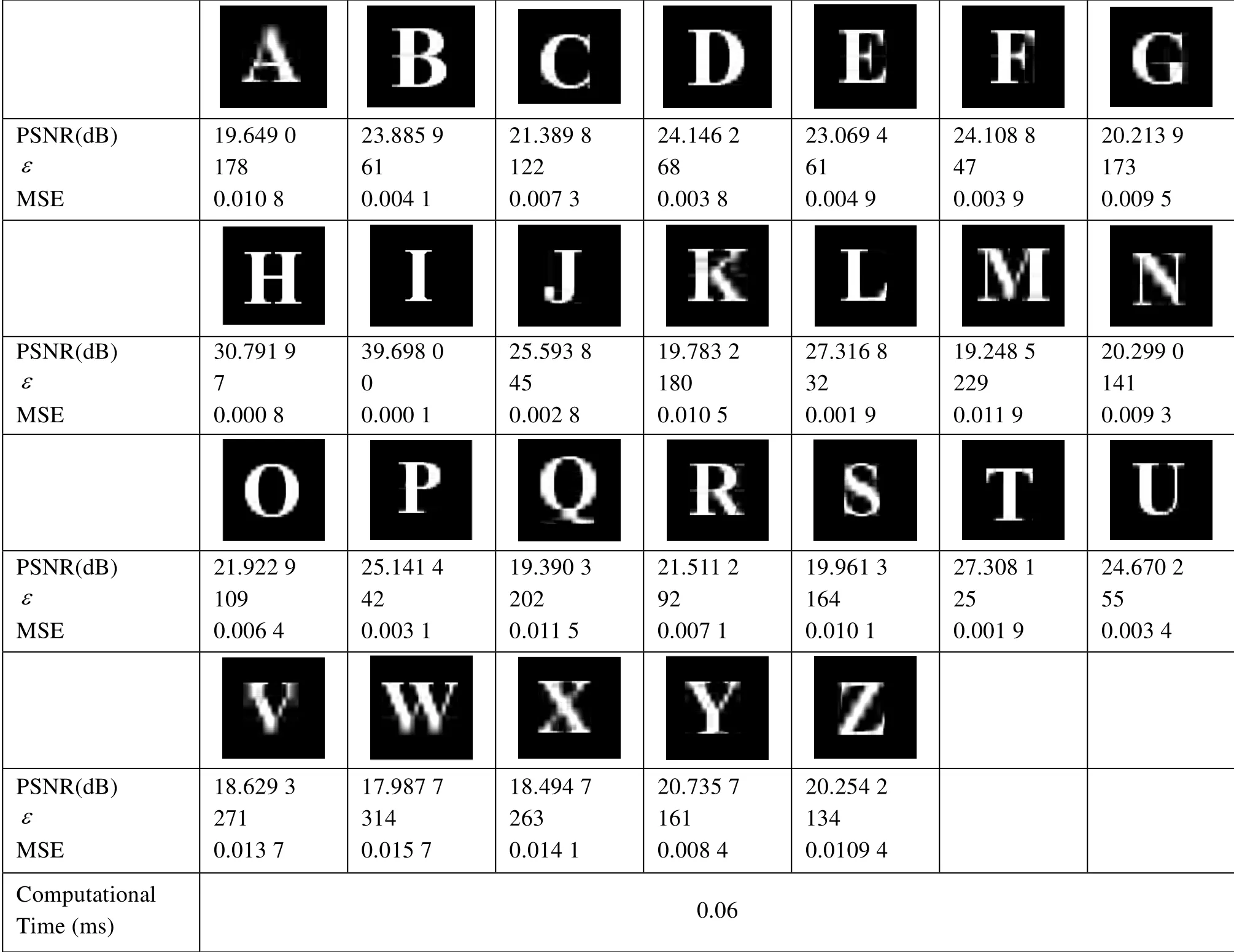
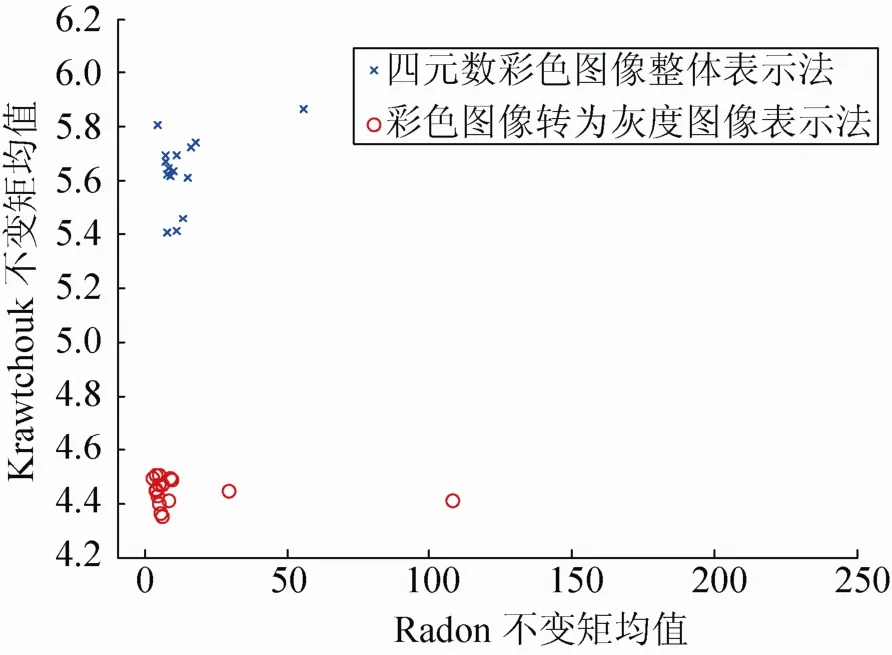
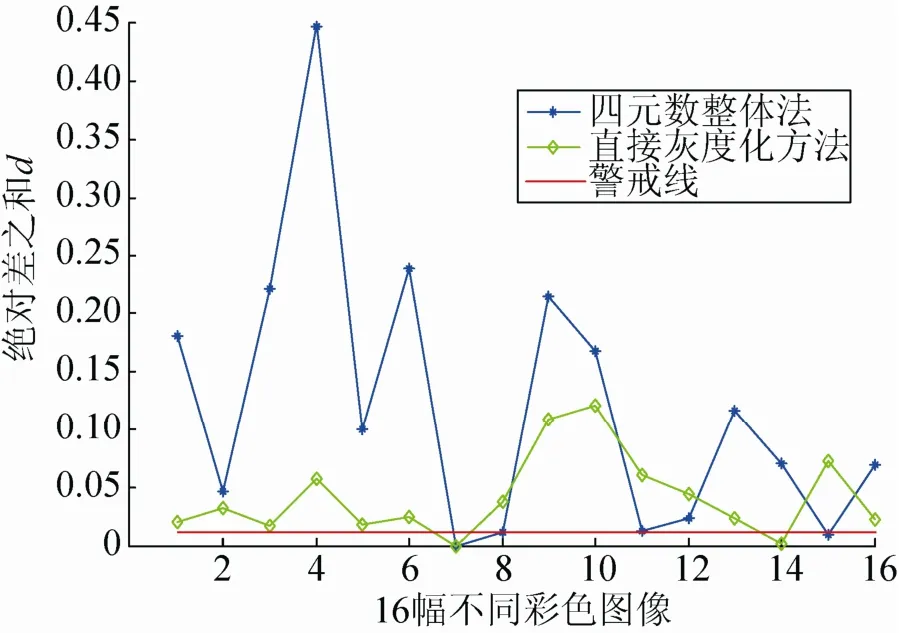
NMF为当前的图像分解提供了一条新的路径。其基本原理可以描述为:任意给定一个非负矩阵 Vn×m,NMF可以寻找出一个非负矩阵Wn×r和另外一个非负矩阵Hr×m,使得这样一个非负矩阵就分解为两个非负矩阵的乘积。其中,W称为基矩阵;H称为系数矩阵;r称为基矩阵维数,且满足r< 1.1乘性迭代算法 Lee和Seung[15]首次提出了使用乘性迭代的方法来解决NMF问题,采用KL散度,其目标函数形式为: 其中,F表示目标函数;i、j表示二维矩阵的行和列数。 泊松噪声模型下的迭代规则: 其中,α,u,i,k,v 分别表示二维矩阵的行或列数(即二维矩阵中的坐标位置)。 该算法与梯度下降、交替最小平方算法相比,需要更多的迭代步骤,因此收敛速度较慢。因为NMF本身不是一种全局最优化的方法,所以就有可能得不到全局最优的解。 1.2梯度下降算法 迭代算法如下: 其中,f(Wk,Hk)表示二维矩阵的基矩阵和系数矩阵;εW和εH是步长;∇Wf(Wk,Hk)和∇Hf(Wk,Hk)表示对目标函数f(Wk,Hk)求偏导。梯度下降算法εW和εH的选择与其收敛性有极大的关系。此算法对其初始值特别敏感,如果随机取初始值,往往得不到令人满意的结果,因此步长的选择和初始值的选取决定着梯度下降算法的设计优劣。 1.3交替最小平方算法 该算法的理论基础在于:在解决最优化KL散度目标函数的问题中,如果只针对W矩阵或H矩阵来说其是凸函数,但同时对W矩阵和H矩阵而言并不是凸函数。所以可以在固定一个矩阵的条件下,对另外一个矩阵进行最小平方计算。其迭代算法如下: 交替最小平方算法中,为了保证数据的非负性,将负值强制为0。这在一定程度上增加了数据的稀疏性,使该算法的计算量小了一些。 为了验证以上3种不同NMF算法的收敛性和分解后的重构误差,本文以64×64Lena灰度图像为例进行说明,实验结果见图 1、2。实验环境:CPU Intel pentium4 3.2 GHz、内存2 G、Windows 7操作系统。 图1 3种NMF算法的收敛速度曲线(mm:乘性迭代;prob:梯度下降算法;als:交替最小平方算法) 图2 3种NMF算法的分解后的重构误差曲线(mm:乘性迭代;prob:梯度下降算法;als:交替最小平方算法) 图3 基矩阵维数r取不同值的误差曲线 由图1~3可知:NMF中,在相同迭代次数下采用交替最小平方算法其收敛速度效率明显优于乘性算法和梯度算法;然而对分解后的灰度 Lena图像进行重构时,其交替最小平方算法产生的重构误差最大,而采用梯度算法产生的重构误差最小。基矩阵维数r的取值也非常重要,若r取值较小,计算运行速度会加快,但经过NMF分解后的矩阵重构误差会增大;若要减小分解后的重构误差,则需增大基矩阵维数r的取值,此时计算速度则会降低;因此NMF算法中收敛速度和矩阵的重构误差是一对矛盾,近年来关于NMF的应用中,对于灰度图像或彩色图像分解后的图像重构及分解效率方面的文献报道较少。本文采用乘性NMF算法对二值图像、灰度图像分别在基矩阵维数r取不同值时,对其图像重构误差和计算时间效率进行了仿真实验分析,这为本文将NMF算法应用到彩色图像零水印中提供了参考依据,实验结果见图4~7。 图4 26个大写字母组成的二值图像测试样本(单个字母大小128×128) 图5 26个大写字母二值图像的重构结果 图6 字母E的重构结果 图7 灰度图像baboon的重构结果 使用峰值信噪比PSNR、均方误差MSE及绝对差ε对原始图像和重构后的图像进行度量,则: 式(5)~(8)中,I(x,y)和I′(x,y)分别表示原始图像和重构后的图像在(x,y)处的灰度值。 以上实验结果表明对大小为 128×128的二值图像,基矩阵维数r>10时;大小为256×256的灰度图像,基矩阵维数r>20时,其图像重构误差和计算时间效率均达到了理想效果(对于一幅256×256的图像,重构后的PSNR大于20 dB,及重构时间小于 10 ms在图像识别中是完全可以接受的),那么将其应用到彩色图像零水印中其不可见性和水印的嵌入、检测计算时间也是完全可以满足的。 目前的彩色图像数字水印算法,大部分处理过程都是先将彩色图像转换为单通道颜色模式即灰度图像,再基于灰度的方法设计水印的嵌入和提取操作。这种方法损失了彩色图像大量的色彩信息,同时又没有利用到图像各颜色通道的空间关系信息,影响到水印检测时的精度。四元数是一般复数的推广,其相关理论已经成功应用于彩色图像去噪、图像分割以及相关模式识别领域。采用四元数表示彩色图像其优势在于:在多维的空间上将彩色图像三个通道的像素作为一个矢量进行整体的处理,而非将三个通道分别处理或直接进行灰度化,考虑了各个彩色图像每个通道之间的相关性,将四元数理论应用于彩色图像零水印算法中,有助于对图像进行更精确的表述。 一般一个四元数q可以表示为: 其中a,b,c,d∈R;i,j,k分别代表四元数的 3个虚部的单位向量,并且满足以下的运算法则: 其中,a为四元数q的实部;i×b+j×c+k×d 为q的虚部;令q的实部为0,3个虚部分量分别表示彩色图像R、G、B三通道即:a=0,b=R, c=G,d=B ,则一幅彩色图像IRGB(m,n)可以表示为: 任意的一个四元数q=a+ib+jc+kd=(a+ib)+(c+id)j=u+vj=u+j×conj(v)其矩阵形式为: 其中,conj表示四元数的共轭;u,v,conj(u),conj(v)对应的矩阵形式为:conj(u)=[a−b;ba];conj(v)=[c−d;dc],将4个矩阵形式代入到Q矩阵中,得到四元数实矩阵W的表示形式: 根据式(12)RGB彩色图像的实矩阵表示为: 图 8~9给出了四元数实矩阵整体彩色图像表示法及彩色图像转换为灰度图像表示法的图像聚类实验结果(以 Radon变换不变矩和 Krawtchouk不变矩为特征描述质,Radon变换不变矩详见文献[11]),实验结果说明,实矩阵整体彩色图像表示法在类间距的聚类效果明显优于彩色图像转换为灰度图像表示法(类间距越大、类内距越小,聚类效果越好),为彩色图像零水印采用四元数实矩阵整体表征图像提供了依据。 图8 16幅不同的彩色样本图像 图9 以Radon不变矩均值和Krawtchouk不变矩均值为特征值下的16幅不同彩色图像的聚类图 3.1零水印生成及注册过程框图 零水印生成及注册过程具体步骤如图10所示: 步骤1. 分别提取原始彩色载体图像的R、G、 B三分量并对其进行非负矩阵分解; 步骤2. 将NMF分解后的三分量系数矩阵H分别在第三方认证机构(CA中心)进行注册; 步骤3. 使用四元数实矩阵整体法来表征原始彩色载体图像,得到四元数数字矩阵; 步骤 4. 提取四元数数字矩阵的 Krawtchouk低阶不变矩(Krawtchouk低阶不变矩详见文献[7])作为特征向量并在CA中心进行注册; 步骤 5. CA中心对特征向量及用户信息加盖时间戳后,宣布原始彩色载体图像已在版权保护之下。 3.2零水印提取与检测过程 给定原始图像矩阵V,其矩阵大小为m×n,经过NMF分解后得到基矩阵W(大小为n×r)和系数矩阵H(大小为r×m),r为基矩阵维数。具体模型如下: 图10 水印生成及注册过程 其中,vi为V的第i列;hi为H的第i列;由式(15)可知原始图像矩阵的每一列与分解后的系数矩阵每一列一一对应。 根据以上公式推论可知:原始图像矩阵 V遭受剪切攻击时,仍可以利用矩阵 V中剩余未被剪切部分恢复出完整基矩阵 W;然后根据保留的系数矩阵H,重构原始图像矩阵。为使基矩阵W存在唯一的解,系数矩阵V的最小秩应等于NMF分解的维数,即T≥r。 零水印提取和检测过程具体步骤如图11所示: 步骤1. 在第三方版权认证中心(CA)按照时间戳提取保存的系数矩阵HR,HG,HB。 步骤2. 对待检测彩色图像是否受到剪切或涂抹攻击进行预判,若遭受剪切或涂抹攻击则从未受损彩色局部图像提取VR,VG,VB矩阵(原始彩色图像R、G、B三分量的局部矩阵),否则执行步骤4。 步骤3. 根据VR,VG,VB数字矩阵,从系数矩阵HR,HG,HB得到与之对应的局部矩阵,,,然后按照式(17)、(14)完成对受损彩色图像的重构。 步骤4. 将待检测彩色图像或重构图像用四元数实矩阵表示,计算该实数字矩阵 10个低阶Krawtchouk不变矩,并将其作为特征向量B。 步骤5. 求出特征向量B与零水印算法注册阶段在CA中心的特征向量A的绝对差之和,即: 若d≥ε并且时间戳与CA中心提供的信息不符(ε为经验阈值系数,实验中取值为0.01)则验证结束,说明待检测图像中不含有水印信息;否则,待检测彩色图像中水印信息存在。 图11 水印提取过程 为了验证所设计零水印算法的有效性,本文以Baboon彩色图像(大小256×256)为宿主图像(见图12),通过Matlab 8.0仿真软件完成以下3组实验结果。实验 1是原始彩色图像遭受常见典型攻击后的实验结果,见表1;实验2是对Baboon彩色图像进行不同比例的剪切和涂抹攻击后的实验,结果见表2;实验3是为了验证对于其他图像是否会出现误判的情况所作的误检率验证实验(采用四元数整体法和直接灰度化方法),宿主图像采用图8的16幅图像,实验结果见图13,由实验结果可知使用四元数整体法的彩色图像零水印算法相比直接灰度化或单通道(R、G、B取其中一个通道)的算法在零水印检测以及误检率方面性能都有一定的提高(采用四元数整体法其绝对差d的数值明显高于直接灰度化处理的方法,说明其区分度相对较大,水印检测时不易产生误判;其中图 8中第3行第1列的彩色图像采用直接灰度化的方法会导致误检,而四元数方法其区分度依然很大)。 图12 Baboon原始彩色图像 表1 常见典型攻击测试结果 表2 抗剪切、涂抹攻击测试结果 图13 采用四元数整体法和直接灰度化方法的误检率曲线图 为了提高零水印算法抵抗存在信息量丢失的各种攻击(剪切、涂抹、行列移除等)的能力,本文将NMF和四元数理论相结合构造出一种抗剪切攻击的零水印算法。算法利用NMF的局部感知全局的特性,对受损后的图像进行重构,并通过对二维图像大量的仿真实验寻找非负矩阵分解后基矩阵维数r的选择及迭代次数之间的折中;由实验结果可知使用四元数整体法的彩色图像零水印算法相比直接灰度化或单通道(R、G、B取其中一个通道)的算法在零水印检测以及误检率方面性能都有一定的提高。下一步的重点是研究NMF算法和四元数整体表示图像在计算量上的相关快速算法,以满足实时性的要求,从而进一步对零水印系统进行优化。 [1] 温泉, 孙锬锋, 王树勋. 零水印的概念与应用[J].电子学报, 2003, 31(2): 214-216. [2] 吴伟民, 丁冉, 林志毅, 等. 基于混沌的医学图像篡改定位零水印算法[J]. 计算机应用研究, 2014, 31(12): 3685-3688. [3] 曲长波, 杨晓陶, 袁铎宁. 小波域视觉密码零水印算法[J]. 中国图象图形学报, 2014, 19(3): 367-371. [4] 谢勇, 张金龙, 张雯. 一种基于奇异值的抗打印/扫描的彩色图像零水印方案[J]. 包装学报, 2014, 16 (3): 11-13. [5] 马建糊, 何甲兴. 基于小波变换的零水印算法[J]. 中国图象图形学报, 2007, 12(4): 582-585. [6] 陈伟琦, 李倩. 基于DWT-SVD的图像双零水印算法[J]. 计算机工程与科学, 2014, 36(10): 1992-1996. [7] 张春凯, 杨德志, 丛佩丽. 基于 krawtchouk矩和NSCT变换的鲁棒性零水印算法[J]. 计算机应用与软件, 2014, 31(3): 282-285. [8] 冯银波, 陈善学. 基于四元数域的彩色图像双重零水印算法[J]. 计算机应用与软件, 2014, 31(9): 264-267. [9] 吴伟民, 丁冉, 林志毅, 等. 基于细胞自动机与奇异值分解的零水印算法[J]. 计算机应用, 2014, 34(6): 1690-1693. [10] 赵玉霞. 基于混沌系统与提升小波的抗剪切攻击的彩色图像盲水印算法[J]. 工程图学学报, 2010, 24(4): 216-219. [11] 何冰. 基于Radon变换不变矩和小波提升的水印算法[J]. 计算机与数字工程, 2011, 39(2): 125-128. [12] 张鑫, 徐光宪, 付晓. 基于面包师变换的抗剪切扩频水印算法研究[J]. 计算机应用研究, 2012, 29(6): 2246-2248. [13] Lin C, Pan J S, Liao B Y. Parity modulationbased watermarking resisting to cropping [C]//Proc of ICICIC 2007. Kumamoto: IEEE, 2007: 294. [14] 邓晓政, 焦李成, 卢山. 基于非负矩阵分解的谱聚类集成 SAR图像分割[J]. 电子学报, 2011, 12(39): 2906-2909. [15] Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization [J]. Nature, 1999, 401: 788-791. [16] Zhang T P, Fang B, Tang Y Y, et al. Topology preserving nonnegative matrix factorization for face recognition [J]. IEEE Trans on Image Processing, 2008, 17(4): 574-584. [17] 韩绍程, 张兆宁. 一种基于子采样的混合域稳健零水印算法[J]. 图学学报, 2013, 34(3): 21-24. [18] 韩绍程, 张红颖. 基于 QR分解的彩色图像自嵌入全盲水印算法[J]. 图学学报, 2013, 34(3): 346-351. A Zero Color Image Watermarking Resisting Strong Cropping Attacks Using Quaternion Representation He Bing1,2 For some zero color image watermarking methods are insufficient for several attacks of information loss, a zero color image watermarking algorithm based on nonnegative matrix factorization and real matrix of quaternion is proposed. Firstly, three components (R, G, B) are extracted from color image and each component is decomposed. Secondly, the coefficient matrix decomposed is registered in the copyright center and the real matrix of quaternion is used to represent the original color image, also the krawtchouk invariant moments of the real matrix is calculated. Finally, some krawtchouk invariant moments are used to design and construct zero watermarking information. The experimental results show that original color image under strong shear can be recovered by residual shear part. When the area of shearing color image exceed 80%, watermark information can still be extracted correctly. This performance in image clustering and watermark error detection rate by using the quaternion to represent the whole color image is better than usingeach of three channels of color image processing or gray image directly. quaternion; zero watermarking; color image; invariant moments; nonnegative matrix factorization TP 391 A 2095-302X(2015)06-0909-11 2015-05-05;定稿日期:2015-09-08 陕西省教育厅科研计划资助项目(14JK1248);渭南师范学院第二批特色学科建设资助项目(14TSXK06);渭南市科研发展计划资助项目(2015KYJ-2-1);渭南师范学院科研计划资助项目(15YKS010) 何冰(1982–),男,陕西合阳人,讲师,硕士。主要研究方向为智能图像数据处理、信息安全研究。E-mail:hebing126@126.com

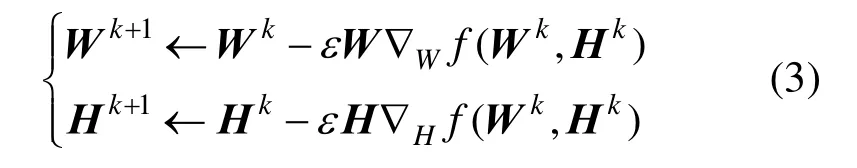
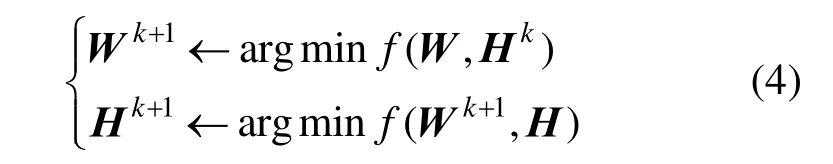







2 四元数彩色图像表示



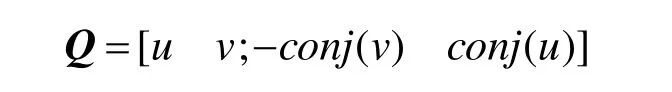
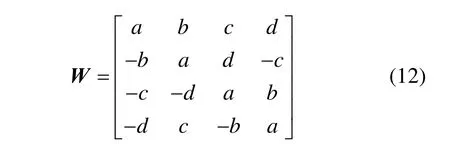


3 本文算法的实现过程






4 实验结果和分析过程



5 结 论
(1. Department of Physics and Electronic Engineering, Wei Nan Normal University, Weinan Shaanxi 714099, China; 2. Center of X Ray Detection and Application of ShaanXi, Weinan Shaanxi 714099, China)
