平底刀底面加工叶片进排气边

张　春， 宁　涛， 沈云超， 陈志同

(北京航空航天大学机械工程及自动化学院，北京 100191)

平底刀底面加工叶片进排气边

张春， 宁涛， 沈云超， 陈志同

(北京航空航天大学机械工程及自动化学院，北京 100191)

平底刀加工叶片进排气边的传统方法以刀具侧刃切削工件，由于叶片进排气边处曲面沿着截型线切线方向曲率半径较小，当走刀方向沿着截型线切向时，加工带宽较小。对影响凸曲面加工带宽的因素进行研究发现，使用平底刀底面进行切削可以提高叶片进排气边处加工带宽，由此提出了用平底刀底面加工进排气边的刀具定位方法，通过优化两个刀具定位参数使加工带宽达到最大。以某航空发动机叶片进排气边为例进行仿真加工，结果表明该方法可有效增大叶片进排气边处的加工带宽。

平底刀；叶片进排气边；刀具底面；加工带宽

叶片的进排气边为连接叶片的叶盆和叶背的过渡区域，该区域近似为一狭长柱面状的复杂凸曲面，叶片进排气边几何形状及尺寸精度对叶片的气动性能有着重要的影响[1]。目前叶片的进排气边多采用球头刀或圆环面刀按螺旋走刀方式进行加工[2]，球头刀的定位方法相对于圆环面刀更为简单，但加工效率较低，沿螺旋线依次走刀加工虽然可以减少非切削走刀路程，但没考虑进排气边曲面曲率的特点，易造成叶身刀轨冗余[3]。为此，郝炜等[4]提出了叶片进排气边避让方法，把叶片进排气边从叶身剥离出来进行单独加工，但并未给出加工叶片的进排气边的方法。黄魏等[5]根据叶片进排气边曲面的特点以圆环面刀具的内侧作为切削刃单独加工叶片进排气边，虽然能提高叶片进排气边的加工效率，但这种刀具不适用于叶身的加工，叶身的加工需要额外的刀具，因此无法避免由换刀带来的“接刀痕”。

目前，五轴数控加工的研究工作主要集中在加工凹曲面上，而对凸曲面加工方法的研究较少。平底刀加工凸曲面时，传统刀具定位方法通常将定位点选在刀具侧刃上。Fan和 Ball[6]以二次曲面对设计曲面进行近似逼近，研究了侧偏角对切削带宽的影响，指出将侧偏角调整到一个合适的位置时可以实现多触点加工。樊文刚等[7]把平底刀前端抬高，将刀具偏转一个负的前倾角使刀具后端紧密地贴合凸曲面来增大加工带宽，然而这种方法增加了一个额外定位参数，将使刀位优化更加复杂。王瑞秋等[8]在加工凸曲面时为了避免刀具与曲面干涉将平底刀底部设计成中凹形状达到多点切触从而获得较大的加工带宽。杜鹃等[9]根据曲面的曲率特性采用“曲率匹配法”来选择合适的刀具，并采用“格点法”来进行局部干涉检验。以上所使用的环面刀都是利用刀具侧刃加工进行数控编程，没有考虑到刀具底部在曲面(特别是凸曲面)加工过程中对加工带宽的影响。

在采用等参数法或螺旋走刀方式进行刀轨排列时，一行刀轨的带宽由该行刀轨上所有刀位点处的最短带宽决定。在加工叶片类曲面时，由于叶片进排气边曲面曲率特点，在加工该区域时，如采用传统的刀具定位方法，在该区域的加工带宽将大大减小，导致一行刀轨的带宽从叶背或叶盆到进排气边急剧缩小，而叶片的进排气边过渡区域面积相对于整个叶片面积较小，在刀轨规划中可能造成叶身刀轨冗余，这将降低叶片加工效率。为此本文提出了一种新的叶片进排气边加工方法，将叶片进排气边进行单独加工并将刀具定位点选在平底刀底面来达到刀具底面参与切削目的。

1　平底刀加工叶片进排气边几何模型的建立

1.1加工原理

由于加工带宽精确的计算较为复杂，为定性地说明平底刀底面加工叶片进排气边的基本原理，将图1所示叶片的进排气边简化为一半径为 rs的半圆柱面 S(u,v)。当刀具定位点选在刀具底部时，如图2所示，走刀方向沿周向，刀具半径为R，刀心点为OT，刀具上的定位点C到刀轴距离为l，柱面上任一点的法矢为 n，加工残高 h，则偏置曲面。点a, b, c, d为刀具边缘与偏置曲面的交点，这4个点围成的阴影部分为刀具的实际工作面，柱面在该刀触点处的加工带宽为根据几何关系有：

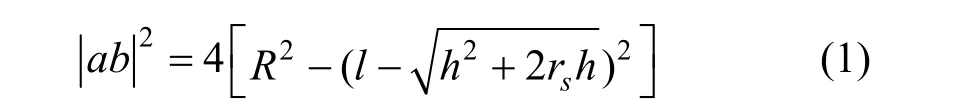
从式(1)可以看出加工带宽和刀具半径，加工残高，设计曲面曲率半径，定位点到刀轴的距离这4个参数有关，其中刀具半径、残高、设计曲面的曲率半径越大，定位点到刀轴的距离越小，加工带宽越大。对于叶片类复杂曲面，叶片进排气边沿叶宽方向的曲率半径极小，而叶身的曲率半径较大，加工时定位点到刀轴的距离l越大越易产生加工带宽从叶身到叶缘急剧变窄的现象。

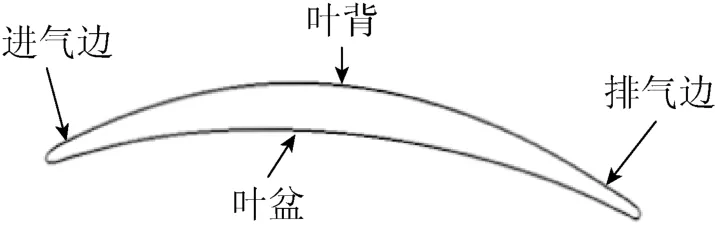
图1　叶片横截面示意图

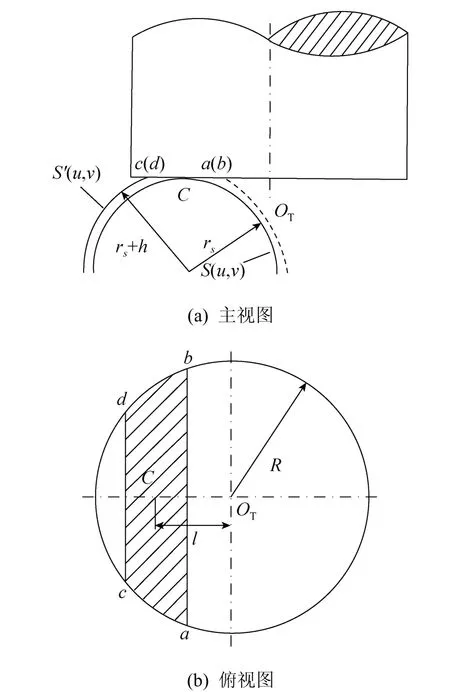
图2　平底刀底部加工圆柱面示意图

1.2工件局部坐标系和刀具坐标系的建立

如图3所示，点C为设计曲面S(u,v)与刀具的切触点，建立工件局部坐标系C(XL,YL,ZL )，轴XL沿曲面S(u,v)在点C处u向偏导方向，轴ZL为沿曲面S(u,v)在点 C处外法线方向，轴 YL满足YL=ZL×XL。为确定刀具与曲面的位置关系，建立刀具坐标系OT(XT,YT,ZT)，OT为刀心点，轴ZT沿刀轴方向，轴XT在刀具底部平面内，轴 YT满足YT=ZT×XT。图3中R为刀具半径，r为刀具圆角半径。

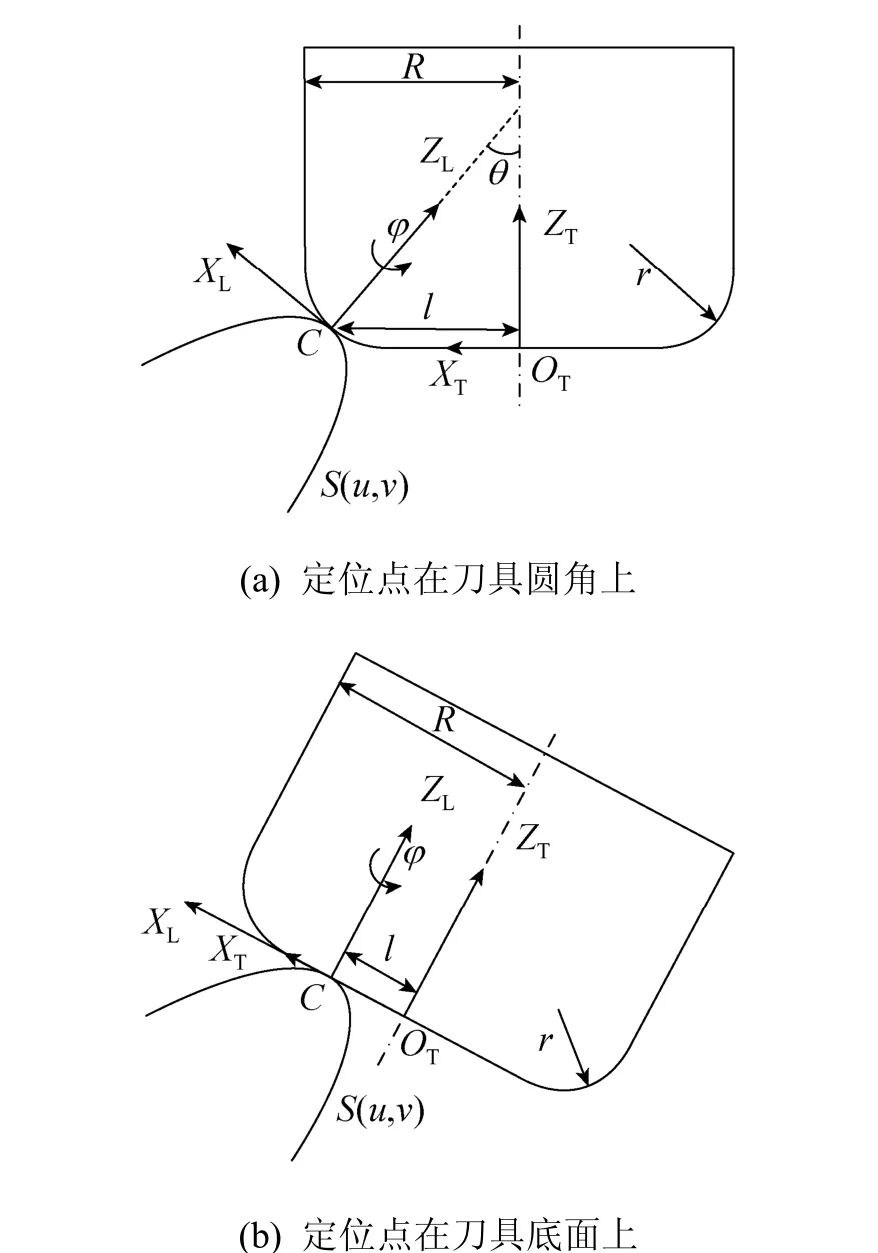
图3　平底刀加工凸曲面刀具定位示意图

刀具与曲面S(u,v)的切触点C与刀具的定位点重合。刀具的定位参数包括定位点距刀轴的距离 l和刀具绕轴 ZL轴旋转的侧偏角ϕ。其中定位点可以在刀具圆角或底部选取。

当刀具的定位点在其圆角部分上时，如图3(a)所示，选择圆角上的不同点作为定位点时，刀具的前倾程度不同，前倾角θ等于轴ZT与轴 ZL的夹角，并满足：

当0θ=，0ϕ=时定义为刀具初始位置，此时刀具坐标系和工件局部坐标系在各个对应坐标轴上分别同向。设分别表示沿轴XT,YT,ZT,XL,YL,ZL正方向的单位矢量，由几何知识可知刀具坐标系到局部坐标的旋转变换关系为：

其中，

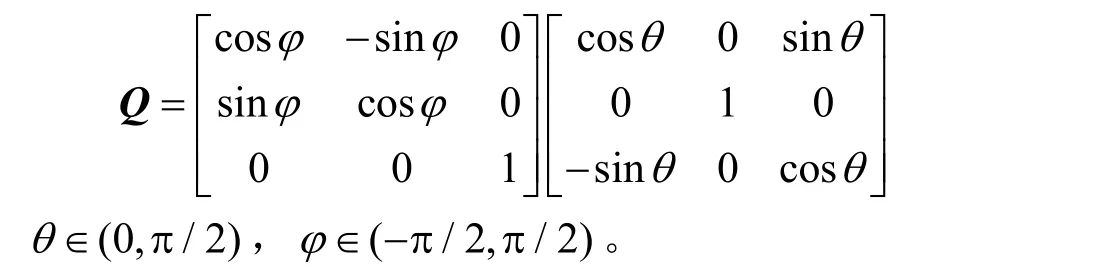
设任意一点 P在刀具坐标系下的坐标为(xt,yt,zt)，在工件局部坐标系下的坐标为(xl,yl,zl)，由几何关系可知：

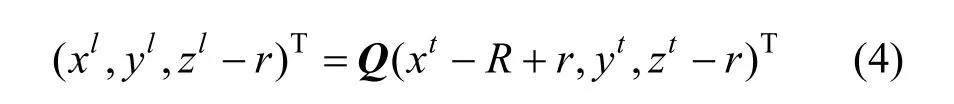
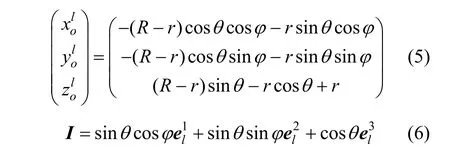
当刀具定位点在刀具底部时，如图3(b)所示，刀轴矢量I与曲面在定位点处的法矢同向，此时刀具的定位点由该点到刀轴的距离 l确定，l满足0＜l≤R−r ，任意一点P在刀具坐标系下的坐标为(xt,yt,zt)，在工件局部坐标系下的坐标为(xl,yl,zl)，其关系为：

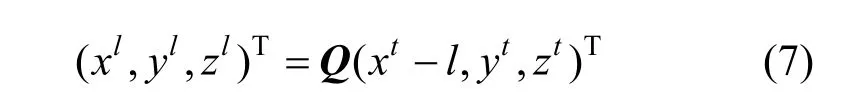
工件局部坐标系下的刀心坐标(xol,yol,zol)和刀轴矢量I可表示为：

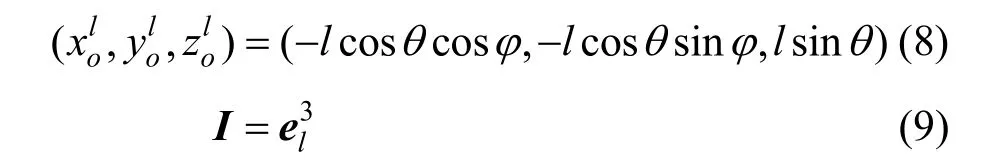
2　定位参数对加工带宽的影响

根据第1节可以看出刀具在工件曲面的位置姿态由两个定位参数确定：ϕ和θ(定位点在刀具圆角上)或ϕ和 l(定位点在刀具底面上)。下面分析刀具定位参数对加工带宽的影响。

2.1定位点对加工带宽的影响

本文主要研究定位点在刀具底部时的情况，此时θ设为0°。不失一般性，本文选用文献[10]所提供的工业凸曲面进行刀具位姿参数分析。采用刀具半径R=5 mm圆角半径r=1 mm平底刀对该曲面进行试切，设刀具切削方向沿等参数线v=0.5方向走刀，设置公差带为(0 mm, 0.01 mm)，过切误差e1=0 mm，欠切误差 e2=0.01 mm，图4是参数(u, v)=(0.5, 0.5)处的加工带宽 w随 l不同时的分布情况，需要说明的是本文所计算的带宽是指参数带宽。从中可以看出随着定位点离刀轴越近，加工带宽越大，当达到某一值时，切削带宽几乎不变，考虑到切削性能，定位点不能离刀轴太近，因为此时定位点处的刀具的回转半径很小，会造成切削线速度很小的不良工况。在忽略切削性能时，图 5为 4个不同定位点的刀具实际有效切削区域和相应的加工带宽图，可以发现当定位点离刀轴的距离l约等于2.0 mm时，切削带宽几乎不再增加，然而当l=1.0 mm和l=0 mm时已发生了刀心参与切削的现象，切削性能将下降。

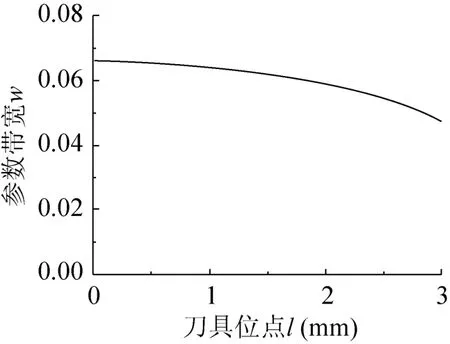
图4　刀具位点对加工带宽的影响

2.2侧偏角对加工带宽的影响

侧偏角对加工带宽有着重要的影响，图6为当定位点距离刀轴的距离l不同时，由不同侧偏角所带来的加工带宽变化图。从图6可以看出，当l一定时，加工带宽随着侧偏角变化的分布趋势相同，加工带宽产生了两个峰值点，分布在侧偏角为 0°的两侧。另外还可以发现l对达到最大带宽时的ϕ几乎无影响。

图7为当l=2.7 mm时，左右带宽和总带宽图，当侧偏角从90°到0°变化时，随着侧偏角的减小，左带宽几乎不变，右带宽增大，切削总带宽增加。随着侧偏角的继续减小，当达到某一值时，左带宽开始减小，其减小量较右带宽的增大量大，导致切削总带宽减小，在该侧偏角处产生一个带宽极大值。当侧偏角从–90°到0°变化时亦然。

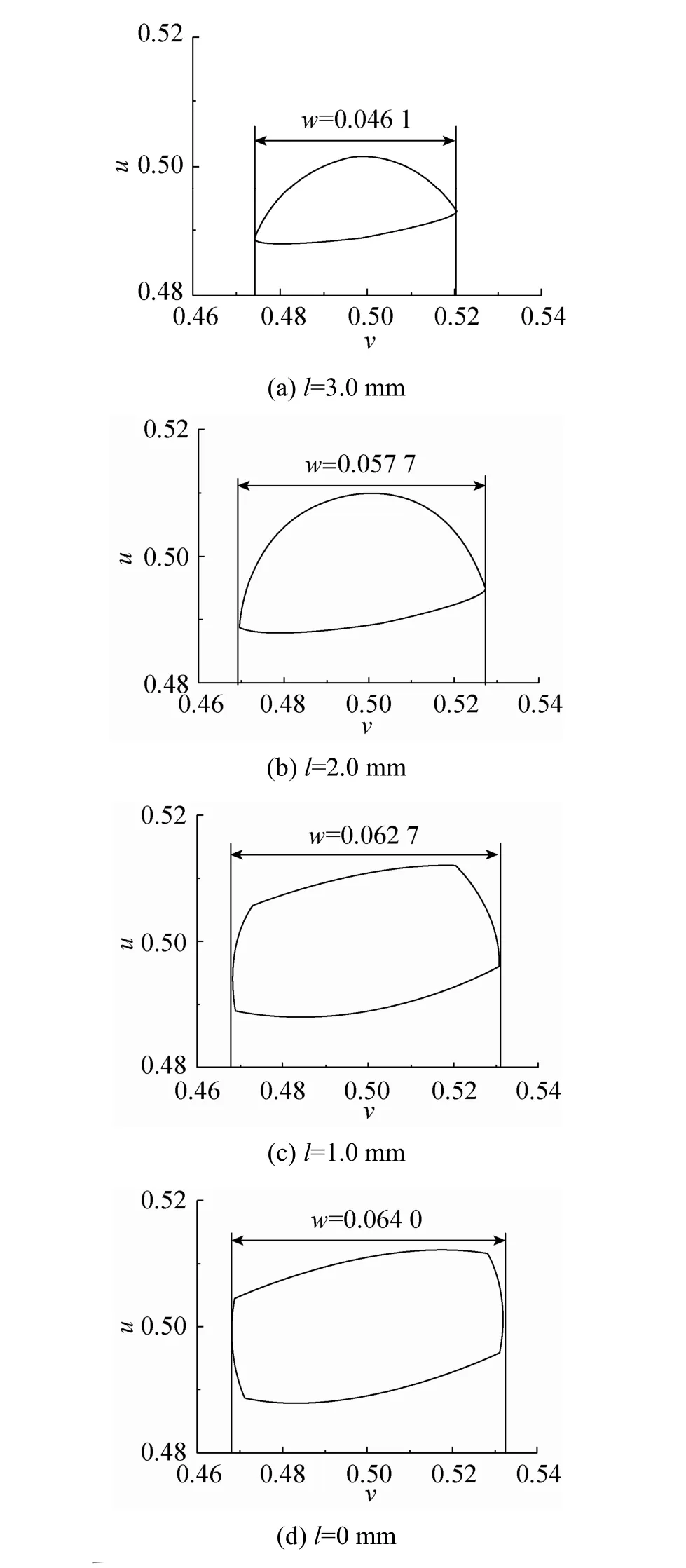
图5　定位点对刀具工作区域及带宽的影响

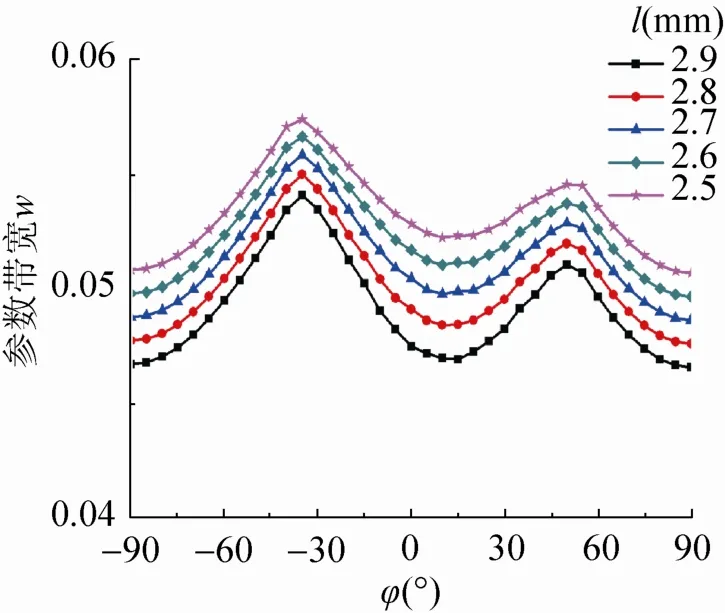
图6　定位点和侧偏角对切削带宽的影响

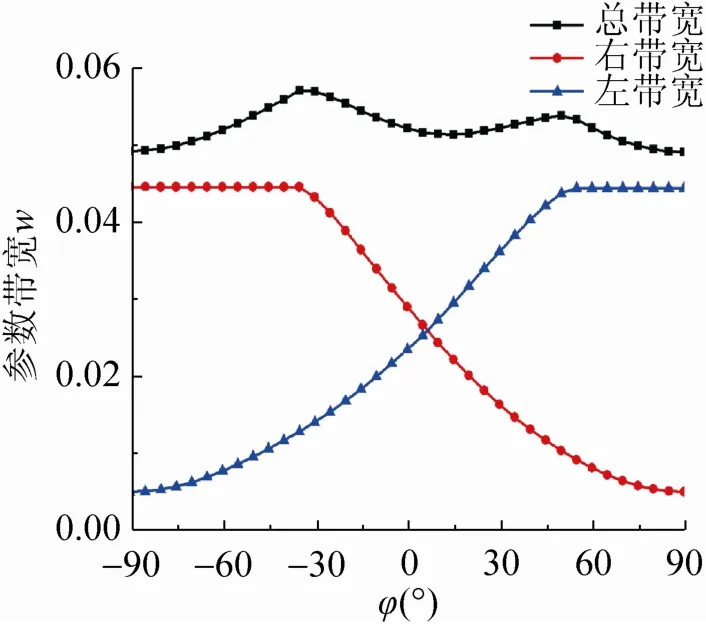
图7　l=2.7 mm时侧偏角对左右带宽的影响

3　刀位优化计算方法

3.1刀位优化数学模型

最短距离线对法能够将刀位的计算与干涉检验结合起来[11]，因此本文采用最短距离线对法进行误差计算。设刀具到曲面的有向距离线段表示为其中n为离散精度，参数θ与 l的关系可由式(2)表示。为达到加工质量要求，对于任意刀具位姿，应满足3个条件：①每条有向线段的有向距离不小于过切误差 e1，否则发生干涉；②应至少存在一条有向线段其有向距离不大于欠切误差 e2；③刀具底面上的定位点要达到切削线速度要求l≥re。最大加工带宽的刀位优化模型可以简单的表示为：

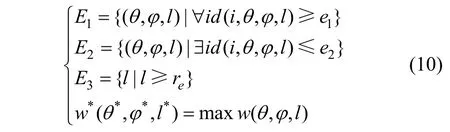
其中E1,E2,E3分别表示满足条件①～③的刀位位姿的集合，w表示加工带宽。当刀具定位点选在刀具底部时，实际上只需对参数l和ϕ进行优化。

3.2刀位优化

叶片进排气边并非是一个绝对的凸曲面，平底刀底面只能加工平面或凸曲面，进排气边上的某些凹面部分只能采用传统的定位方法进行加工，以下是针对叶片进排气边加工刀位优化的具体算法。

根据2.2节分析结果可知， l对最优侧偏角ϕ的影响不大，在求解最优ϕ时，首先对 l进行离散lj(j=0,1,2,…,m−1)，对每个 lj求出使带宽达到最大时ϕjopt，在搜索最优ϕjopt时，可将搜索区间分为两部分，分别从初值为 −90°和 90°变步长搜索出2个极大值点，取使带宽较大的那个极值点作为 lj对应的最优ϕjopt值，如此重复求出所有 lj所对应的ϕjopt，最后取其平均值作为最终的ϕ。

在求得最优ϕ值后，对l进行优化，此时需考虑2点：①切削线速度不应过低，这要求l越大越好；②切削带宽，局部凸曲面上曲率较大部分的切削带宽不应过多的小于其他部分的切削带宽，否则易造成刀轨冗余，也不应大于其他部分的切削带宽，过大不仅降低切削性能而且过大的切削带宽对于整个叶片进排气边的刀轨规划无较大的意义。其具体算法如下：

步骤 1. 离散一行刀轨刀触点Ci(i=0,1,2,…, n−1)；

步骤 2. 定位点在平底刀侧刃时，初计算每个刀触点的最小前倾角 θi及带宽wi；

步骤4. 求Ec中每个刀触点处刀具位姿参数组合(θi,ϕi)和最小带宽

需要说明的是先优化ϕ后优化l是在保证加工带宽的要求下尽可能地提高切削线速度。

4　试验及验证

以某航空发动机叶片为例，该叶片的进排气边处的厚度约为0.2 mm，公差带设置为(– 0.001 mm，0.02 mm)，采用单向走刀沿着等 v参数线生成刀轨，并对等参数线进行等弦高离散得到各刀触点，弦高误差为0.001 mm，计算精度为1×10–6。加工叶片进排气边区域的参数范围为u∈(0.49～0.52)，v∈(0.1～0.9)，加工所选刀具半径R=5 mm，侧刃圆角半径为r=1 mm。

图8为在等参数线v=0.5时，本文算法与一般宽行加工算法在叶片进排气边处整行刀轨加工带宽比较图。可以看出，在叶片的进排气边处，由于截型线切向方向曲率急剧减小，叶片的进排气边处切削带宽低于叶身的切削带宽，对整个叶片的刀轨规划带来了严重的限制，采用本文算法后，消除了由于叶片进排气边加工带宽对导轨规划的限制，可以提高加工效率。

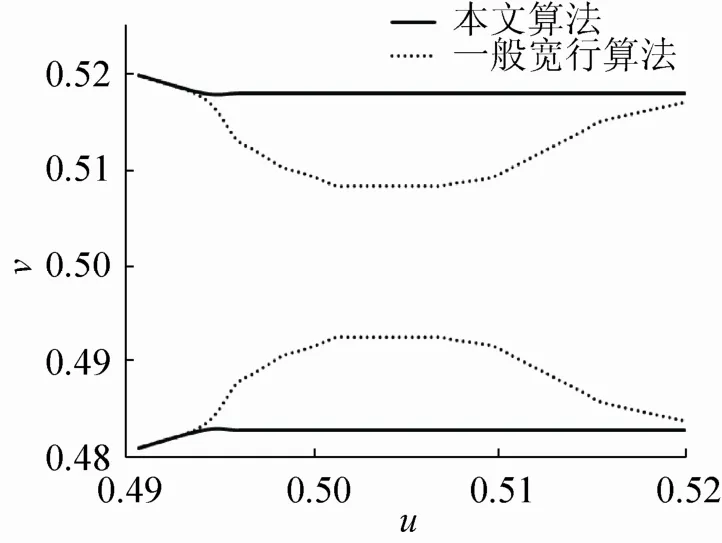
图8　加工带宽比较图

图 9(a)为采用本文方法生成的刀轨，共有 31条刀轨，图 9(b)为 UG算法生成的刀轨，共有 48条刀轨，本文方法生成的刀轨数明显的减少，加工效率将得到提高。图10为本文算法在VERICUT软件中的加工仿真图，本文所提出的加工方法能够满足加工质量要求。

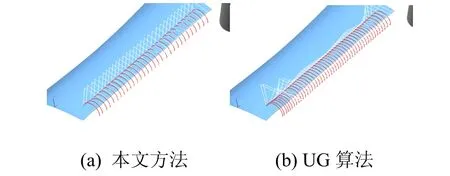
图9　本文算法与UG算法生成刀轨对比

5　结　论

通过对平底刀底面加工一般凸曲面的研究发现，刀具定位点离刀轴距离越近，加工带宽越大，当达到某一值时，加工带宽几乎不变。将该原理应用到叶片进排气边加工中，可以有效地提高叶片进排气边的加工带宽，从而提高整个叶片的加工效率。该算法通用性好，也适用于其凸曲面的加工。

[1] Arbos-Torrent S, Ganapathisubramani B, Palacios R. Leading-and trailing-edge effects on the aeromechanics of membrane aerofoils [J]. Journal of Fluids and Structures, 2013, 38: 107-126.

[2] Shan C W, Zhang D H, Liu W W, et al. A novel spiral machining approach for blades modeled with four patches [J]. International Journal of Advanced Manufacturing Technology, 2009, 43: 563-572.

[3] 王明海, 李晓鹏. 叶片型面曲率属性对数控铣削加工过程的影响[J]. 航空动力学报, 2013, 28(1): 25-31.

[4] 郝炜, 蔺小军, 单晨伟, 等. 薄壁叶片前后缘加工误差补偿技术研究[J]. 机械科学与技术, 2011, 30(9): 1446-1450.

[5] 黄魏, 陈志同, 陈五一, 等. 用反圆环面刀加工变曲率过渡曲面原理[J]. 北京航空航天大学学报, 2012, 38(8): 1118-1123.

[6] Fan J H, Ball A. Flat-end cutter orientation on a quadric in five-axis machining [J]. Computer-Aided Design, 2014, 53(8): 126-138.

[7] 樊文刚, 李建勇, 黄泽华, 等. 多点切触加工在复杂凸曲面中的应用[J]. 西安交通大学学报, 2012, 46(3): 53-58.

[8] 王瑞秋, 陈五一, 金曼. 多点切触加工中的局部干涉分析[J]. 北京航空航天大学学报, 2006, 32(5): 580-584.

[9] 杜鹃, 闫献国, 田锡天. 复杂曲面五轴加工局部干涉处理技术研究[J]. 图学学报, 2012, 33(1): 113-121.

[10] Warkentin A, Ismail F, Bedi S. Comparison between multi-point and other 5-axis tool positioning strategies [J]. International Journal of Machine Tools & Manufacture, 2000, 40(2): 185-208.

[11] 倪炎榕. 环面刀具五坐标数控加工复杂曲面优化刀位计算与图像显示[D]. 北京: 北京航空航天大学, 1999.

Machining the Leading and Trailing Surface of Turbine Blades by the Bottom of the Flat-End Cutter

Zhang Chun,Ning Tao,Shen Yunchao,Chen Zhitong
(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

Traditional method of machining leading and trailing edge surface of turbine blades with a flat-end cutter is to use the side edge of the cutter to cut the workpiece, by which the strip width will be very narrow when the cutter traces along the tangential direction of blade cross-section curve, because the cross-section curve′s curvature radius of leading and trailing edge surface is too small. By studying on the factors influencing the machining strip width of convex surfaces, it was found that the strip width will be wider if the bottom of flat-end cutter is used. A new flat-end cutter positioning method using the bottom of the flat-end cutter to cut the leading and trailing edge surface is proposed to maximize the strip width by optimizing the two cutter positioning parameters. Machining simulation experiment on an aero-engine demonstrates the feasibility of this method in increasing the strip width of leading and trailing edge surface.

flat-end cutter; leading and trailing edge surface; bottom of flat-end cutter; strip width

TP 391

A

2095-302X(2015)06-0834-06

2015-06-24；定稿日期：2015-07-31

国家重大科技专项(2013ZX040111031)

张春(1988–)，男，四川巴中人，硕士研究生。主要研究方向为数控编程技术。E-mail：zhangchun_buaa@163.com