Excel软件辅助概率论与数理统计教学

孙晓玲，王 宁

（合肥师范学院数学与统计学院，安徽 合肥 230601）

1 引言

本科概率论与数理统计课程是应用性较强且有重要实践意义的公共基础课也是数学专业的必修课，作为数学的一个重要分支，它是研究随机现象统计规律性的一门学科。这门课程概念、公式、定理、结论多而杂，很多问题计算量较大，数据处理也较繁杂，即便使用计算器往往也要耗费很长时间，学生将大量的时间和精力用于繁杂的手工数学运算，却很难真正理解计算结果在统计中的应用［1］。另外，传统概率论与数理统计的教学通常依靠学生通过做习题来巩固和理解教学内容，课程中应用性较强的内容不能实际动手设计和分析，严重影响和制约了教学效果。教师的黑板式教学缺乏分析结果的可视化直观表现。Excel是大家熟悉的办公系统OFFICE的组件，相对于SPSS、SAS、SYSTAT等统计软件，它的普及率高且容易获得。新版Excel 2010具有非常强大的数据处理和统计分析功能，可以通过简便的操作完成复杂的数据分析、统计及管理工作。Excel 2010提供了覆盖面极广的统计分析工具库，涵盖了概率论与数理统计教材中常用函数分布。其图形可视化功能可以对图形进行静态与动态的可视化设计，能够把曲线、曲面的形成和变化过程准确的模拟出来，对于概率计算和统计数据的处理和分析，只需通过简单自学就可以实现上机操作。另外，Excel 2010数据表不但可以很方便的嵌入到PPT文件中进行教学演示还可以嵌入到网页中让学生自主实验，这些功能可给概率论与数理统计课堂上的演示教学带来极大的便利。本文主要介绍在概率论与数理统计教学中如何巧用Excel软件辅助教学，提高课堂的教学效果和教学效率［1－3］。

本文在概率论与数理统计教学中利用Excel 2010内置函数和公式辅助教学。需要调用Excel 2010的函数和公式。将传统的黑板或PPT演示的例题搬到Excel 2010表格上做，这样既能够节省大量复杂的运算时间，又有助于理解和记忆教学过程中涉及到的定义、定理和公式，加强了理论学习的效果，更重要的是教师通过在Excel表格上改变参数或数据，能够引导学生观察动态的计算结果变化和相应的图形变化，便于教师进行课堂演示教学和学生自主探究学习。

要实现在课堂上利用Excel 2010进行复杂计算，验证定理或直接在Excel 2010表上讲授例题，提高课堂教学效果和教学效率，需要教师事先利用Excel设计制作包括概率计算、图形绘制和数据分析等各种类型的教学模板。通过这些教学模板在课堂上进行理论或实践教学，可以达到事半功倍的效果。现举例说明Excel在辅助课堂教学中的应用以及相应的教学模板的设计制作方法［4－6］。

2 应用实例

2.1 教学内容分析

“随机变量的分布函数”它是概率论与微积分学的桥梁，通过分布函数就能利用微积分这个有利工具研究概率问题。另外，分布函数还是进行统计推断、统计检验的基础，因此该部分内容也为统计部分的学习打下基础。通过本小节的学习也可以帮助学生逐步掌握计算随机变量取值概率的方法；培养学生的分析能力，综合能力，并能使学生认识到Excel软件在概率论与数理统计课程学习中的辅助作用。

2.2 教学案例

利用Excel演示分布函数值的计算不仅能让学生理解分布函数的概念及应用，同时使学生认识到熟练利用Excel软件能够很大程度的提高学习效率、提升学习效果，促进学生创新精神和创造能力的培养。

2.2.1 分布函数的概念

定义：设X为随机变量，对任意实数x，称函数F（x）＝P｛X≤x｝，（－∞＜x＜＋∞）

为随机变量X的分布函数。

关于分布函数定义的两点说明：

（I）几何意义：如果将随机变量X看作数轴上随机点的坐标，那么分布函数F（x）在点x处的值就表示随机变量X落在区间（－∞，x］上的概率。

（II）由定义，对任意实数x1＜x2，随机变量X落在区间 （x1，x2］内的概率为：

随机变量X落在区间（x1，＋∞）内的概率为：

同样地，还可以计算随机变量X落在其它任意区间内的概率，因此，只要知道了随机变量X的分布函数，就能够完整地描述随机变量的统计规律。

2.2.2 离散型随机变量的分布函数

若X是离散型随机变量，且分布律为P｛X＝xi｝＝pi，i＝1，2，3，...，则有F（x）＝P｛X≤x｝。即F（x）是随机变量X取小于等于x的诸值xi的概率之和，故又称F（x）为累积分布函数。

例1：小王每天开车上班，从他家到单位的途中总共经过10个交通岗，假设他在各个交通岗遇到红灯的事件是相互独立的并且概率都是0.7。

问：小王至多遇到6次红灯的概率是多少？

【分析】小王每天开车上班，从他家到单位的途中总共经过10个交通岗，将通过每个交通岗看作一次随机试验，遇到红灯的概率相同且每次试验结果相互独立，假设他在各个交通岗遇到红灯的事件是相互独立的并且概率都是0.7，以X表示他遇到红灯的次数，因为X的取值无非只有0，1，2直到10，因此是离散型随机变量。又由于若将通过每个交通岗看作一次试验，根据假设遇到红灯的事件概率相同且每次试验结果相互独立，完全符合二项分布的特点，因此 是服从二项分布故X～b（10，0.7）。

传统的解题过程

由于随机事件｛至多遇到6次红灯｝＝｛X≤6｝，根据二项分布律公式P｛X＝x｝＝（1－p）n－x（x＝0，1，...，n）以及离散型随机变量分布函数的计算公式可以得到F（6）＝P｛X≤6｝＝（0.7）x（0.3）10－x，这里出现一个问题，由于这里出现了组合数，继续常规计算的话，下面的计算量将会非常复杂，几乎无法完成，到这里不建议大家用常规方法来计算但是要想继续得到结果，这里可考虑用Excel软件来辅助计算。Excel软件包含了大量的数学函数，它不仅是很好办公的软件，还是解决概率统计问题的有力工具，相比于其它常见数学和统计软件来说，Excel软件更容易获得和使用，在这道题中，我们可以利用Excel软件中的二项分布函数计算X的分布律，分布函数值，再利用该软件生成分布律的柱状图以及分布函数的线图，下面我们来看下该软件的辅助计算。

利用Excel辅助解题

利用Excel的二项分布函数：BINOMDIST（m，n，p，L）可计算随机变量X的分布律和分布函数值，还可利用该软件生成分布律条形图和分布函数的线图。由图1可知若遇到红灯的概率为0.7，则小王至多遇到6次红灯的概率为F（6）＝P｛X≤6｝＝0.3504。通过图1－－图4能够更清晰地看出概率计算原理及分布函数的意义。

（注：BINOMDIST（m，n，p，L）函数中各参数含义

m为实验成功的次数，

n为独立实验的总次数，

p为一次实验中成功的概率，

L是一个逻辑值，用于确定函数的形式，若L值为TRUE返回分布函数，FALSE返回分布律。）

图1 随机变量X的分布律和分布函数值

在单元格B5到B15中输入二项分布概率计算公式“＝BINOM.DIST（A5，＄C＄2，＄C＄3，0）”，注意公式中对参数n，p的引用需要使用Excel的绝对引用格式，在单元格C5到C15中输入二项分布概率计算公式“＝BINOM.DIST（A5，＄C＄2，＄C＄3，1）”来计二项分布的累计概率值，计算出所需概率后可以绘制分布律图形和累计分布图来展示不同事件发生概率的情况。图形生成方法是，先选中所需绘图的数据单元格B5到B15，选择菜单中插入－＞图表－＞柱形图即可。

图2 制作柱形图菜单

阶梯图制作较为复杂，首先选择两列数据A5—A15以及C5—C15生成散点图，然后在Excel 2010的布局工具栏下选择误差线，添加误差线并做修饰后可以得到阶梯图4。

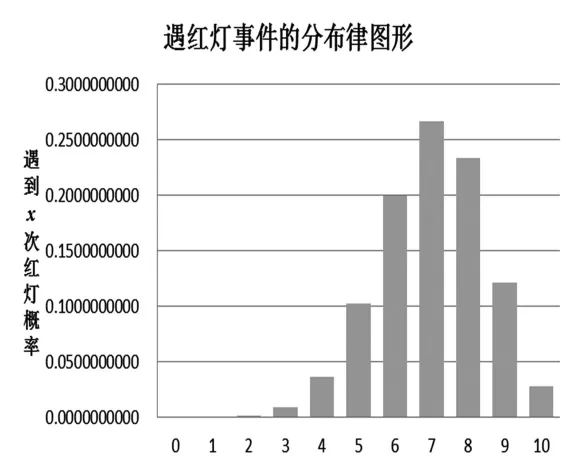
图3 分布律柱形图

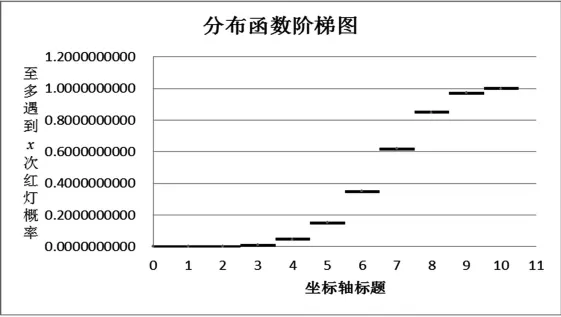
图4 阶梯图

【小结】

（I）由该例可以看出，要计算小王上班途中至多遇到6次红灯的概率，只需计算遇红灯次数小于等于6的概率，即P｛X≤6｝＝F（6）就可以了。

（II）Excel 2010在增加易用性同时有很强的处理概率统计问题的功能，利用其内置函数可以高效处理二项分布问题。另外Excel 2010软件的计算与统计分析功能非常强大并且使用简单，能够较好的提高学习效率、增强理论的实用价值。

3 结束语

《概率论与数理统计》是一门应用性极强的统计学基础课程，需要进行大量的数值计算面对大量的数据。传统的黑板讲授和纸上作业方式已经无法适应现代数学理念和教学内容的改革，课堂教学不应也无法回避使用计算机软件的数据处理。把易学易懂、普及化程度高并具有强大数据处理与分析功能的Excel软件用于《概率论与数理统计》的辅助教学，不仅能使抽象的教学内容变得直观，复杂的数值计算瞬间完成，还能够大大提高课堂教学的效率和效果、丰富教学内容，让难学的知识变得更加有趣。

［1］张雪峰，张晋熙，吴悦坚，王思翰.EXCEL统计分析在概率统计教学中应用［J］.曲阜师范大学学报，2013，39（4）：114－118.

［2］侯晓丽，吴富锁，李利鸿，郑丰.关于EXCEL课程教学改革的思考［J］.农业网络信息，2013，2：126－127.

［3］林忠.利用Excel的统计函数进行概率分布计算机实验［J］.西昌学院学报（自然科学版），2006，20（2）：71－73.

［4］徐雅静，谢栋梁，曲双红，卢金梅，汪远征.利用EXCEL改革《概率论与数理统计》课堂教学［J］.大学数学，2013，29（4）：4－8.

［5］程烈.利用EXCEL计算概率及概率分布［J］.产业与科技论坛，2013，12：171－172.

［6］林彤.EXCEL在概率论与数理统计中的应用［J］.东北电力大学学报，2013，6：52－55.