基于带决策者偏好多目标优化的证券组合投资研究

李章晓，宋 薇，张兴义

（1.徽商职业学院会计系，安徽 合肥 230022；2.安徽大学 计算机科学与技术学院，安徽 合肥 230039）

1 引言

证券投资组合是分散投资风险的有效途径，在发达的证券市场，如何得到最佳的投资组合是一项极具挑战但却有重要实际意义的工作。诺贝尔经济学奖获得者马克威茨（Markowitz）于1952年提出了著名均值方差模型第一次定量地说明了如何衡量投资组合的收益和风险水平［1］，从而为最佳证券投资组合的研究提供了重要的理论依据，是现代金融理论研究的创举和转折点。在他的均值－方差模型中，证券期望收益率均值和期望收益率方差是衡量一种投资组合好坏的两个指标，其中期望收益率均值刻画投资组合的收益大小，而期望收益率方差刻画投资组合的风险。一项好的证券投资组合应该使其期望收益率均值最大，而期望收益率方差最小。因此，证券投资组合可以表示为下面的均值－方差两目标投资组合优化问题：

其中，W＝（w1，…，wn）T，wi，1≤i≤n，为总资产投资在第i个证券的权重，n为投资组合包含的证券数目，R为收益率矩阵，∑为收益率的协方差矩阵，w0为投资者投资于无风险资产的权重（以下仅考虑w0＝0的情形，即投资者仅进行有风险的证券投资）。由（1）式可以看出，寻找最佳的投资组合即是寻找一个W，使E（R）最大且σ2最小，同时W需要满足限制性条件＝1，且wi≥0，即不允许卖空。

为解决此多目标优化问题，研究人员陆续引入了许多策略和算法。如，万丽英等人引入了中心路径跟踪算法求解均值－方差两目标投资组合优化问题［2］；崇曦农等人首先把该多目标优化问题转化单目标问题，并利用拉格朗日乘数法求解［3］；卞蓓丽利用了多目标蚁群算法和多目标模拟退火算法解决此问题［4］等。在解决该问题的众多方法中，多目标优化领域中的经典优化算法深受研究人员的喜爱，被广泛地应用于求解均值－方差两目标投资组合优化问题，为投资者提供良好的投资选择，如快速非支配排序遗传算法（NSGA－II）［5］。对于大多数的证卷投资来说，由于投资收益和投资风险总是互相矛盾的（即投资收益的增加往往以伴随着风险的增加为代价），因此多目标优化算法将得到在不同投资风险下的大量投资组合。而投资者往往仅仅关注少量的最佳投资组合，因此投资者需要花费大量的时间和精力从多目标优化算法所获得的大量投资组合中选择理想的投资组合。

为了简化投资者后续选择的大量工作，本文引入了多目标优化领域中的一个新的研究成果，基于决策者偏好的多目标优化算法（KR－NSGA－II）。与经典的多目标优化算法NSGA－II相比，KR－NSGAII不是以搜索整个Pareto前沿面上大量均匀分布的解为目标，而仅搜索决策者感兴趣的Pareto面上的部分解。基于锐思金融数据库中提取的股票信息对KR－NSGA－II进行了实证分析，数值实验结果表明KR－NSGA－II仅搜索投资者感兴趣的投资组合，从而为投资者节省了进行选择的大量时间和精力。

2 带决策者偏好的多目标优化算法（KR－NSGA－II）

在多目标优化领域，NSGA－II以其高效实用而被广泛用于求解许多领域内的多目标优化问题，如车辆路径优化［6］，电力系统稳定器参数优化［7］，武器装备供应商的选择与评价［8］等。NSGA－II［9］包含以下几个主要步骤：（1）随机产生大小为N的初始种群；（2）利用二元竞技从种群中选择父代；（3）利用交叉、变异操作从父代产生N个后代；（4）当前种群和所产生的N个后代构成大小为2N的混合种群；（5）对混合种群进行快速非支配排序，为每个个体指定Pareto次序；（6）计算混合种群中每个个体的拥挤距离；（7）利用个体的Pareto次序和拥挤距离从混合种群中选择N个个体作为下一代种群；（8）以上步骤不断循环直到达到算法的终止条件（通常可以用最大迭代次数作为终止条件）。对于含有2或3个目标的多目标优化问题来说，NSGA－II可以较好地搜索到多目标优化问题的整个Pareto最优前沿面。

与 NSGA－II不同，KR－NSGA－II仅以搜索 Pareto最优前沿面上决策者感兴趣的部分解为目标。在决策者具体偏好未知的情况下，Pareto前沿面上的拐点通常是大多数决策者感兴趣的最优解，因此KR－NSGA－II将仅会搜索Pareto最优前沿面上的拐点。在均值－方差两目标投资组合优化问题中，Pareto最优前沿面上的拐点指投资收益与投资风险比值最大的最优投资组合。在证卷投资者偏好的投资组合未知情况下，Pareto前沿面上的拐点对应的投资组合将很大可能会是投资者感兴趣的。

KR－NSGA－II采用与 NSGA－II完全相同算法结构，其唯一区别在于它们从当前种群及其所产生的后代中选择下一代种群采用的策略不同。在KRNSGA－II中，NSGA－II中每个解的拥挤距离被替换为该解与拐点的距离。因此，在KR－NSGA－II选择下一代种群中的解时，若一个解支配另一个解，则将优先选择支配解作为下一代种群中的解；若两个解均为非支配解，则将优先选择离拐点较近的非支配解作为下一代种群中的解［10］。KR－NSGA－II的算法流程如图1所示。

图1 KR－NSGA－II算法流程

3 实证分析与讨论

为验证KR－NSGA－II在求解均值－方差两目标证卷投资组合优化问题中的有效性，本文从锐思金融数据库选择了100支股票在2013－11－04至2013－12－13期间共一个月的信息进行了测试（数据库网址为http：／／www.resset.cn／cn／）。本文采用 Matlab 2009a软件进行了仿真实验，KR－NSGA－II和NSGA－II中参数设置均为：种群规模为100，最大迭代次数为300，交叉概率为1.0，变异概率为0.033。

图2—图6分别给出了 KR－NSGA－II和 NSGA－II两种算法在20、40、60、80、100支股票上选择最优投资组合的优化结果，其中红色圆圈表示KRNSGA－II所得到的最优投资组合，蓝色星号表示NSGA－II所得到的最优投资组合，其中图形中的每个点均表示一个投资组合。从这些图中可以看出，NSGA－II会得到大量的最优证卷投资组合，投资者要想从如此庞大数目的证卷投资组合中选择一个理想的投资组合将花费其大量的时间和精力；KR－NSGA－II仅会搜索到3个最优证卷投资组合，它们分别对应以下三种情形：（1）投资风险最小情况的投资收益；（2）投资风险最大情况下的投资收益；（3）单位投资风险内的最大投资收益（即投资收益除以投资风险的值最大）。在投资者具体的偏好未知情况下，这三种投资组合方式通常都是投资者较喜欢的投资选择。由于KR－NSGA－II仅搜索到三种投资者最可能喜欢的最优的投资组合，从而不需要投资者进行复杂而艰难的选择，为投资者节省了大量的时间和精力。

图2 20支股票的优化结果

图3 40支股票的优化结果

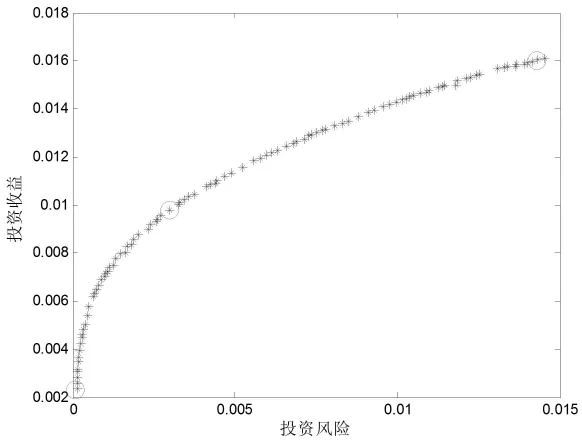
图4 60支股票的优化结果

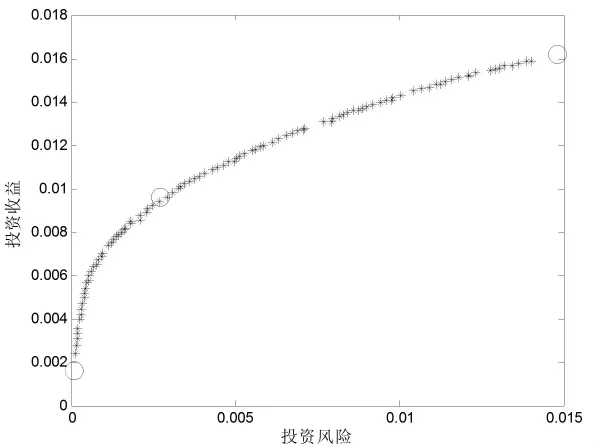
图5 80支股票的优化结果

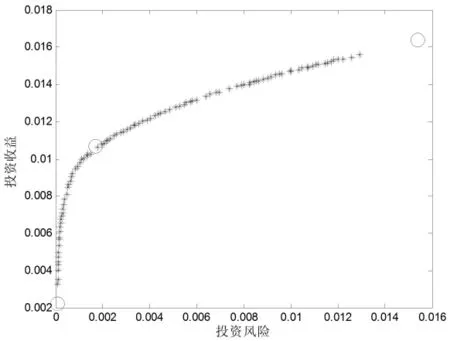
图6 100支股票的优化结果

从图2—图4可以看出，当股票数目较少时（少于60支），KR－NSGA－II所搜索到的三种最优投资组合对应为NSGA－II所搜索到的大量投资组合的三种特殊情形，这说明KR－NSGA－II可以帮助投资者自动选择其感兴趣的证卷投资组合。从图5－图6可以看出，当股票数目较多时（大于等于80支），KR－NSGA－II所搜索到的投资风险最小情况下的投资收益和投资风险最大情况下的投资收益对应的两种证卷投资组合明显优于NSGA－II所搜索到投资组合，由于KR－NSGA－II仅关注搜索这三种投资者最感兴趣的投资组合，因而使算法具有比NSGA－II更好的搜索性能。

通过以上的实证分析可以看出，KR－NSGA－II不仅可以节省投资者进行大量选择的时间和精力，而且当股票数目较多时还可以给投资者提供更好的投资组合，因此KR－NSGA－II在寻找最佳证卷投资组合方面是非常有效且实用的一种方法。

4 结束语

本文为解决投资者需要花费大量的时间和精力从传统多目标优化算法所搜索的大量投资组合中选择最佳投资组合的问题，引入了多目标优化领域一个新的研究成果 KR－NSGA－II，实证分析说明了KR－NSGA－II的可行性。由于 KR－NSGA－II是假定在投资者偏好未知的情况下，因此Pareto最优前沿面上的拐点具有较大可能对应投资者感兴趣的投资组合。在某些情形下，出于自身投资习惯和投资目标的考虑，投资者往往对投资组合具有一定的具体个人偏好，如投资风险不能大于一定范围。因此，如何引入或设计新的多目标优化算法，使其能有效搜索到投资者偏好的投资组合是今后的研究工作之一。

［1］Markowitz H M.Portfolio selection［J］.Journal of Finance，1952，7：77－91.

［2］万丽英，李兴斯，张新芬.证卷投资组合一种多目标优化模型及其算法［J］.数学的实践与认识，2010，40（24）：9－14.

［3］崇曦农，李宏.多目标证卷投资组合决策模型［J］.南开经济研究，2000，4：69－71.

［4］卞蓓丽.蚁群算法在多目标优化的证卷投资组合中的应用研究［D］.广州：华南理工大学，2012，.

［5］孙碧莲.基于多目标优化的投资组合分析［J］.计算机工程与应用，2013，09.

［6］徐慧英，赵建民，张泳，朱信忠.改进NSGA－II算法在车辆路径多目标优化问题中的应用［J］.计算机工程与科学，2010，10：117－121.

［7］张利.NSGA2算法及其在电力系统稳定器参数优化中的应用［D］.西安：西安交通大学，2013.

［8］唐天兵，申文杰，韦凌云，谢祥宏.一种改进的多目标混合遗传算法及其应用［J］.计算机工程与应用，2010，46（22）：242－244.

［9］Deb K，Pratap A，Agarwal S，Meyarivan T.A fast and elitist multiobjective genetic algorithm：NSGA－II［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197.

［10］Bechikh S，Said L B，Ghédira K.Searching for knee regions in multi－objective optimization using mobile reference points［C］／／Proceedings of the 2010ACM Symposium on Applied Computing，2010：1118－1125.