多层边坡的加权位移反分析方法
2015-12-05周光裕唐金董亚奎
周光裕,唐金,董亚奎
(湖南路桥建设集团有限责任公司,湖南 长沙,410004)
在对岩土结构进行分析和计算时,可靠分析结果的获取需要准确的岩土体力学参数作为保证。在大多数的工作中,岩土体力学参数的获取依靠现场土体的原位测试以及室内常规土工试验。而对于碎石土或膨胀土等一些特殊土体,利用常规的试验方法难以获得准确的参数。此时,参数反分析作为一种理论严谨、应用成熟的方法,其优势便显现出来[1–10]。在众多反分析方法中,参数位移反演的优化方法是一种最为普遍的方法。该方法利用监测手段获得岩土体的位移,并建立数值计算模型,对实际位移与计算位移之间的误差即目标函数进行优化,以获得和实际位移相近的计算参数。杜景灿针对含有软弱夹层的边坡,对传统的目标函数进行位移加权处理,提出了软弱层的参数反演方法[1]。将滑坡土体分为3个类别,求得不同位置土体对3个类别的隶属度,并根据每个类别权重构造目标函数[11–19]。
在已有工作的基础上,针对多土层边坡的参数反演问题,提出了新的目标函数,并分析了其敏感性,为多土层边坡的参数反演提供了新的思路。
1 加权位移反演方法
传统位移反分析优化方法的目标函数如下:

式中:xi,xi分别为岩土体的实际位移与计算位移; J为计算参数矩阵; pij为不同类别土体的力学参数。由(1)式可知,随着矩阵J中强度参数的变化,函数f也会相应地变化。调整J中的参数,使

此时矩阵J中的强度参数即为反算的结果。
边坡内部的软弱夹层和结构面的厚度一般较小,若应用(1)式对此类边坡进行反演,其参数及位移变化对f(J)值的影响较小,因此传统的参数反演方法不能对上述类型边坡进行有效反演分析。为此,杜景灿提出了加权的位移反分析方法[1]:

式中λi为各测点位移的加权系数。
为突出软弱夹层或结构面在边坡变形及滑动中的重要作用,加权法给予其较大的位移权重。但是杜景灿并未给出权重的具体计算方法,且当边坡内部软弱层较多或者没有明显软弱层时,该方法难以明确权重的大小。为此,本文针对含有多个软弱层的边坡反演问题,提出了新的加权位移方法。

图1 多土层边坡的位移监测
2 目标函数的构建
对于图1所示的多土层边坡,当图层中含有多个软弱夹层或各土层间的强度参数相差不大而使边坡呈层状滑动时,原有的加权方法就不再适用。
现场监测时,较厚土层中布置的监测点较多,使得厚土层对目标函数f(J)值的影响较大。然而,边坡滑动变形很大程度上取决于厚度较小的软弱夹层或结构面。一些位于边坡上部的土层,厚度虽然较大,但其自身变形较小。因此,有必要对边坡内各土层的位移变形进行计算,使每个土层的位移在目标函数中的敏感度相同。
每个土层的位移可表示为

式中:Xi为第i个土层的自身位移,与其厚度无关; xi为第i个土层中的测点位移; ni为第i个土层中的监测点个数。在目标函数中,将 Xi代替原有的测点位移 xi,这样既可以反映多土层边坡层状滑动的特点,又将各土层的变形作为基本位移单位,避免了其厚度不均带来的误差问题。
边坡中,内部滑动面附近的土体剪应变最大,滑坡的发生是因为滑面上部的土体随着时间的推移,沿着在滑坡发生前就已经开始滑动的滑面发生整体滑移的结果。因此,滑动面附近土体对滑坡的发生与边坡稳定起到重要作用。但是在滑坡发生前,滑动面附近土体的位移并不明显。而处于滑动体处的土体的测点位移较大,究其原因是其下方土体的滑动而导致的自身位移较大,但这并非是自身的变形。因此,在边坡滑动过程中,各部分土体发生位移的原因是不同的。然而,传统的计算方法中并未对于土体位移原因进行分析,这就使得传统的反分析方法无法精确反演出边坡的强度参数。
若简单地将边坡土体分为滑坡体、滑动面及滑坡床,对于不同土体在滑坡过程中的作用,有滑坡面>滑坡体>滑坡床。而对于多土层边坡,对土层进行精确划分是有困难的。因为这3类土体之间是渐变的,界限是模糊的。尤其对于“交界面”附近的土体,在性质上很难单独划分为某一类,往往具有2种土体的性质,需要利用模糊数学对该问题进行描述。
设某一测孔深度为h1,滑动面深为h2。隶属函数是以测点深度为自变量的线性函数。土体的隶属度函数U由子函数μ1、μ2、μ3组成,其分别表示土体对滑床、滑面与滑体的隶属度:
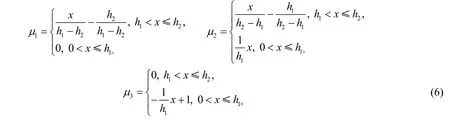
式中:μ1,μ2,μ3分别为某一测点对滑坡床、滑坡面和滑坡体3种土体的隶属度; x为该测点深度。
由函数U可知,当测点分别位于滑坡表面,滑动面和基岩表面时,滑坡床、滑坡面和滑坡体3种土体的隶属度为1。离布置于滑坡表面,滑动面和基岩表面的 3点的距离愈远,滑坡床、滑坡面和滑坡体3种土体的隶属度愈小。隶属度与距离呈线性关系,函数曲线如图2所示。
由式(4)及隶属函数U可知,边坡力学参数反分析优化法的目标函数权重可表示为

目标函数为:
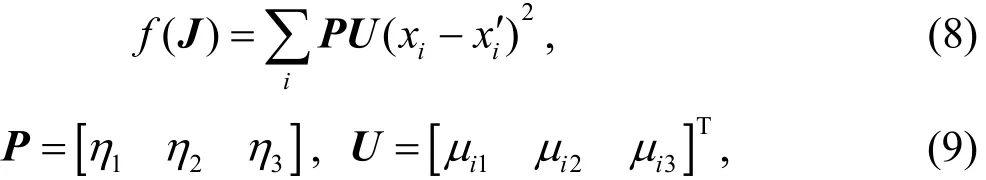
式中:P表征滑坡床、滑坡体与滑坡面对边坡滑动的影响,称为权重系数矩阵; η1、η2、η3分别表示3类土体的位移在反分析过程中权重; U为某测点的隶属度矩阵。
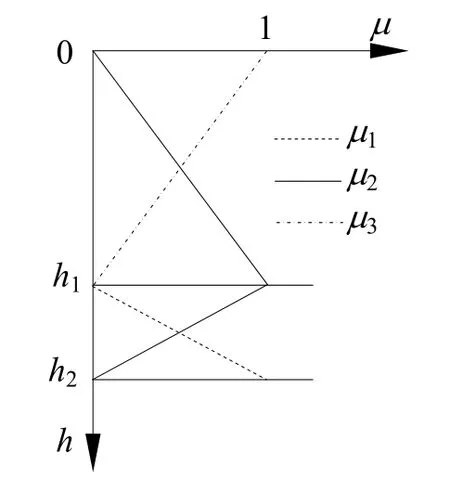
图2 隶属函数曲线
3 结果计算与验证
为了验证新的目标函数对所要反演的边坡强度参数的敏感性,本文利用工程实例计算了图3所示边坡参数改变时的目标函数值,并绘制了目标函数对参数的灵敏度曲线。图3中各测点的实际位移如图4所示,目标函数对参数的灵敏度曲线如图5~6所示。为便于比较,同时计算了按传统的优化法反分析所构造的目标函数的函数值,并给出了灵敏度曲线。

图3 边坡形状及测点位
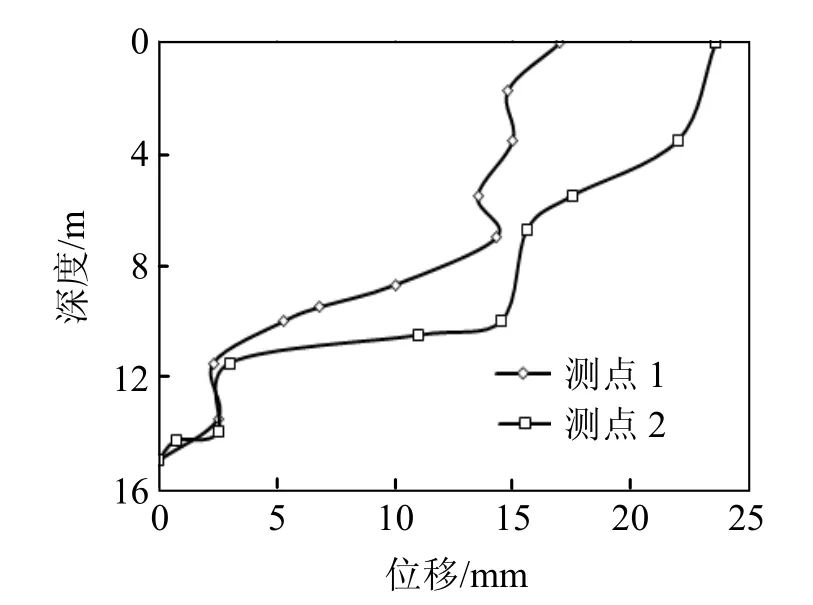
图4 监测点实际位移
目标函数对强度参数的敏感度计算公式为
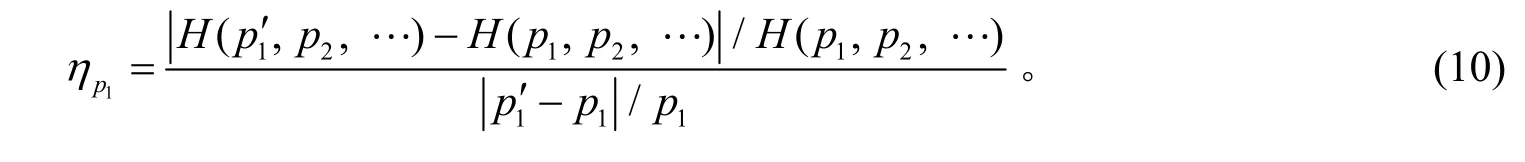
敏感性分析的结果表明,边坡位移对土体初始黏聚力c的敏感度要大于对土体内摩擦角φ的敏感度。就2个目标函数而言,无论对于c或者φ,本文提出的目标函数的敏感度都要大于传统方法的敏感度。说明在利用优化法进行边坡强度参数反分析时,本文的方法具有优势。

图5 目标函数对c值敏感度

图6 目标函数对φ值敏感度
4 结论
传统参数反分析方法进行多土层边坡进行反演时,忽视了边坡的滑动状态受土层参数不同以及滑动面的影响。本文利用加权位移反分析的思想,构造了新的目标函数,并反演了某分层边坡的参数。结果表明,无论对于强度参数c还是φ,使用新的目标函数计算实际位移与计算位移误差时,其敏感度均大于传统位移反演方法,说明新的方法具有更好的反演效果。根据实际工程对本文方法进行验证,得到的反演的结果与试验方法的结果相近。
[1]杜景灿,陆兆溱.加权位移反演法确定岩体结构面的力学参数[J].岩土工程学报,1999,21(2):209–212.
[2]王华宁,吕爱钟.巷道裂隙岩体的损伤参数辨识[J].岩土工程学报,2001,23(5):593–597.
[3]Yang Xiao-li,Qin Chang-bing.Upper bound limit analysis of roof collapse in shallow tunnels with arbitrary cross sections under condition of seepage force [J].Journal of Central South University,2014,21(11):4 338–4 343.
[4]Yang Xiao-li,Yang zi-han,Pan Qiu-jing,et al.Kinematical analysis of highway tunnel collapse using nonlinear failure criterion [J].Journal of Central South University,2014,21(1):381–386.
[5]Yang Xiao-li,Yang Zi-han,Li Yong-xin,et al.Upper bound solution for supporting pressure acting on shallow tunnel based on modified tangential technique [J].Journal of Central South University,2013,20(12):3 676–3 682.
[6]Yang Xiao-li,Zhang Dao-bing,Wang Zuo-wei.Upper bound solutions for supporting pressures of shallow tunnels with nonlinear failure criterion [J].Journal of Central South University,2013,20(7):2 034–2 040.
[7]Yang Xiao-li,Zhang Jia-hua,Jin Qi-yun,et al.Analytical solution to rock pressure acting on three shallow tunnels subjected to unsymmetrical loads [J].Journal of Central South University,2013,20(2):528–535.
[8]Yang Xiao-li,Jin Qi-yun,Ma Jun-qiu.Pressure from surrounding rock of three shallow tunnels with large section and small spacing [J].Journal of Central South University,2012,19(8):2 380–2 385.
[9]Yang Xiao-li,Huang Fu,Wang Jin-ming.Modified image analytical solutions for ground displacement using nonuniform convergence model [J].Journal of Central South University of Technology,2011,18(3):859–865.
[10]Yang Xiao-li,Huang Fu.Influences of strain softening and seepage on elastic and plastic solutions of circular openings in nonlinear rock masses [J].Journal of Central South University of Technology,2010,17(3):621–627.
[11]Yang Xiao-li,Huang Fu.Stability analysis of shallow tunnels subjected to seepage with strength reduction theory [J].Journal of Central South University of Technology,2009,16(6):1 001–1 005.
[12]Yang Xiao-li,Zou Jin-feng.Estimation of compaction grouting pressure in strain softening soils [J].Journal of Central South University of Technology,2009,16(4):653–657.
[13]Yang Xiao-li,Huang Fu.Slope stability analysis considering joined influences of nonlinearity and dilation [J].Journal of Central South University of Technology,2009,16(2):292–296.
[14]Yang Xiao-li,Zou Jin-feng.Displacement and deformation analysis for uplift piles [J].Journal of Central South University of Technology,2008,15(6):906–910.
[15]Yang Xiao-li,Sui Zhi-rong.Seismic failure mechanisms for loaded slopes with associated and nonassociated flow rules [J].Journal of Central South University of Technology,2008,15(2):276–279.
[16]Yang Xiao-li,Guo Nai-zheng,Zhao Lian-heng,et al.Influences of nonassociated flow rules on seismic bearing capacity factors of strip footing on soil slope by energy dissipation method [J].Journal of Central South University of Technology,2007,14(6):842–847.
[17]Yang Xiao-li,Wang Zhi-bin,Zou Jin-feng,et al.Bearing capacity of foundation on slope determined by energy dissipation method and model experiments [J].Journal of Central South University of Technology,2007,14(1):125–128.
[18]高玮,郑颖人.基于遗传算法的岩土本构模型辨识[J].岩石力学与工程学报,2002,21(1):9–12.
[19]孙志彬,杨小礼,黄阜.利用模糊数学与粒子群算法的边坡反分析研究[J].华南理工大学学报,2011,39(6):137–141.
