挖掘机不停车换挡液压系统参数及效率分析

孟忠良 ,余璇

(1.枣庄学院 机电工程学院,山东 枣庄,277160; 2.徐工特种工程机械有限公司,江苏 徐州,221000)

不停车换挡液压系统采用力士乐公司的A4VG变量泵和A6VM变量马达,不停车换挡液压系统对应的行驶驱动系统主要技术指标为最高行驶速度大于50 km/h,最大爬坡度(纵坡)大于20º。在液压传动系统设计中,需要着重考虑液压系统中元件的传动效率,它对工程机械的动力性和经济性有着重要的影响。不停车换挡液压系统由变量泵和变量马达组成,因此,在计算液压系统中元件的效率时,主要是考虑计算变量泵和变量马达的效率。变量泵和变量马达两者的排量、系统压力、传动效率都会随负载的变化而变化[1]。通过理论公式计算变量泵与变量马达的参数及效率,从而分析出泵与马达的排量、压差和效率之间的内在关系,所得的液压系统元件选型及系统匹配如下:主泵流量最大排量qpmax=250 mL/r,最大工作压力Ppmax=37 MPa; 马达最小排量qmmin=60.79 mL/r,马达最大排量qmmax=160 mL/r;马达容积效率ηmv=0.95; 泵容积效率ηpv=0.95; 轮胎滚动半径R=0.53 m; 变速箱传动比i1=1.389; 桥传动比i2=11.29。由此来计算各挡的最高行驶速度、最大牵引力和爬坡能力。

1 各挡最高行驶速度计算

泵的最大流量 Qmax=nmax× qpmax× ηpv=2 200 × 250 × 0.95 × 10-3=522.5 L/min。

(1)前进一挡(低速挡)单个马达获得最大流量Q1max=Qmax/4=522.4/4=130.625 L/min。马达的最高转速 n1max=Q1maxηmv/qmmin=130.625 × 0.95/0.060 79=2 041.35 r/min。最高行驶速度 V1max=0.377 ×n1maxR/(i1× i2)=(0.377 × 2 041.35 × 0.53)/(1.389 × 11.29)=26 km/h。

(2)前进二档(中速挡)单个马达获得最大流量Q2max=Qmax/3=522.3/3=174.17 L/min。马达的最高转速 n2max=Q2maxηmv/qmmin=174.17 × 0.95/0.060 79=2 721.8 r/min。最高行驶速度为V2max=0.377 ×n2maxR/(i1× i2)=(0.377 × 2 721.8 × 0.53)/(1.389 × 11.29)=34.7 km/h。

(3)前进三挡(高速挡)单个马达获得最大流量Q3max=Qmax/2=522.3/2=261.25 L/min。马达的最高转速 n3max=Q3maxηmv/qmmin=261.25 × 0.95/0.060 79=4 082.27 r/min。最高行驶速度 V3max=0.377 ×n3maxR/(i1× i2)=(0.377 × 4 075.0 × 0.53)/(1.389 × 11.29)=52 km/h。

(4)倒挡与前进一挡速度大小相同，方向与其相反，故VDmax=V1max=26 km/h。

2 各挡最大牵引力计算

液压马达启动扭矩:

其中ηm为马达的机械效率,取ηm=0.86,代入数据得MQ=809.5 N·m。牵引力:

其中 η′m为传动系总效率,η′m=0.8。

(1)前进一挡 MQ1=4 × MQ=4 × 809.5=3 238 N·m。P1=(MQ1× i1× i2× η′m)/R=(3 238 × 1.389 ×11.29 × 0.8)/0.53=76.65 kN。

(2)前进二挡 MQ2=3 × MQ=3 × 809.5=2 428.5 N·m。P2=(MQ2× i1× i2× η′m)/R=(2 428.5 × 1.389 ×11.29 × 0.8)/0.53=57.48 kN。

(3)前进三挡 MQ3=2 × MQ=2 × 809.5=1 619 N·m。P3=(MQ3× i1× i2× η′m)/R=(1 619 × 1.389 ×11.29 × 0.8)/0.53=38.32 kN。

(4)倒挡牵引力与前进一挡大小相同,方向相反,故PD=P1=76.65 kN。

由以上计算结果可知,各挡的最高行驶速度和最大牵引力与选型计算时最初设定各档位的最高行驶速度和最大牵引力基本一致,变量泵和变量马达的选型计算也比较合理,同时也实现了最高行驶速度大于50 km/h的技术指标。

3 爬坡能力计算

最大爬坡度(纵坡)大于20º,故以20º为最小角度计算。轮式挖掘机在爬坡阶段,多采用一挡行进,最大牵引力Pn=76.65 kN,G=20.2 t,滚动阻力系数f=0.02(碎石路面)。爬20º坡时总阻力PF=71.43 kN。因Pn＞PF,故轮式挖掘机可以爬上20º的坡。

4 变量泵的效率计算与分析

轮式液压挖掘机不停车换挡液压系统中的液压泵选用的是AV4G型的轴向柱塞变量泵。泵容积效率和机械效率随着排量的减小而迅速减少,其乘积所得的总效率则会显著减少[2]。根据已有研究可知,变量泵的容积效率ηpv和机械效率ηpt可以整理成下面的形式:

式中:ηpv为变量泵的容积效率; ηpt为机械效率; Cs为层流泄露系数,Cs=0.8 × 10-9; Δp为进出口压差; μ为油液动力黏度,μ=0.014 Pa·s; np为泵的转速; Cv为层流阻力系数,Cv=0.2 ×106; β为泵的排量比; Cf为机械阻力系数,Cf=0.01; qpmax为泵全排量; Tc为与进出口压差和转速的一定转矩损失。

由式(3)和式(4)可得,变量泵的容积损失主要由Cs来表示,指从运动副间隙中泄漏的流量。而变量泵的机械损失主要由3方面组成:一是由Cv项来表示,指由油液的粘性所产生的摩擦损失,与np和μ乘积成正比; 二是由 Cf项来表示,指与高、低压移动界面前后的压差成线性比例的摩擦损失; 三是由Tc项表来示,指与工作压力、转速都无关的定量扭矩的损失,此项在这里可以忽略不计[3]。

设定发动机的额定转速值为n=2 200 r/min,代入式(3)和式(4),求得A4VG250型轴向柱塞变量泵的容积效率和机械效率。容积效率曲线如图1所示,机械效率曲线如图2所示。

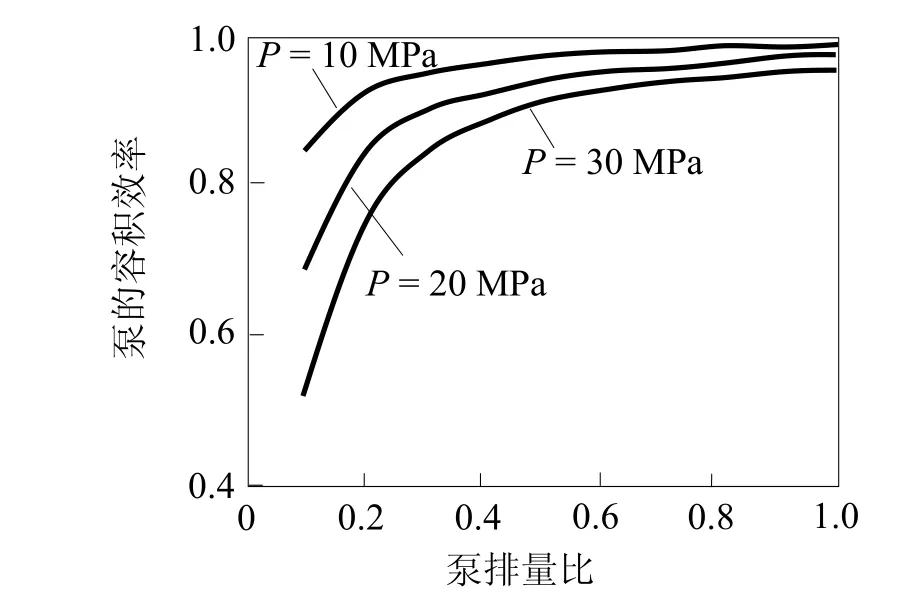
图1 容积效率曲线

图2 A4VG250变量泵的机械效率曲线

又因为

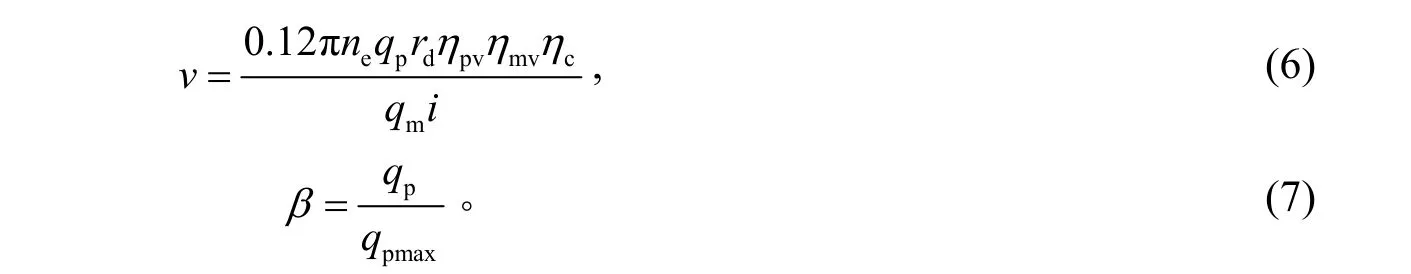
把式(7)代入式(6)可得:

取马达的容积效率ηmv=0.95,泵的容积效率ηpv=0.95,管路效率ηc=0.95,发动机的转速ηe=2 200 r/min。在行驶工况下,单个马达排量为最小排量,挖掘机处不同档位时,马达的总排量qm不同,泵的最大排量qmmax=250 mL/r,总传动比i=15.68,轮边半径rd=0.53 m,把以上参数带入式(8),可得

一档时:

二档时:

三档时:

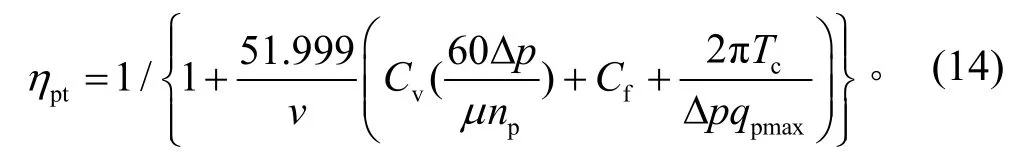
图3 A4VG250变量泵行驶状态容积效率曲线

综合式(9)到式(14)可得泵的容积效率、机械效率和总效率在作业工况下随速度变化的曲线(图3～5)。根据图3、图4和图5分析可得,在每个行驶档位内,随着行驶速度的增大,变量泵的效率也会不断增大。但是,在换挡过程中,液压泵的效率会有所下降。由图3可知,泵的容积效率会随着系统压力的升高而降低,在高速行驶工况下,其容积效率会高于65%; 由图4可知,泵的机械效率会随着系统压力的升高而升高,在高速行驶工况下,其容积效率会高于90%。由图5可知,当轮式液压挖掘机的行驶速度大于10 km/h时,液压泵的总效率则可以达到90%以上。可见挖掘机在行驶过程中,液压泵会处于高效的工作状态,所以当轮式液压挖掘机的行驶速度高于10 km/h,液压泵会有比较高效的工作状态。

图4 A4VG250变量泵行驶状态机械效率曲线

图5 A4VG250变量泵行驶状态总效率

5 液压马达的效率计算与分析

根据液压马达与液压泵相似的效率计算与分析方法,得出液压马达的容积效率 ηmv、机械效率 ηmt和总效率ηm三者的表达式分别如下[4]:式中ηm为马达转速。轮式挖掘机不停车换挡液压系统的变量马达选用的是A6VM160,马达的排量能实现无级调节。设定发动机转速不变,泵处于最大排量时,轮式挖掘机在行驶工况下马达多处于小排量档qm=qmmin=60.79 mL/r,由式(15)、(16)和(17),求得不同车速下马达的容积效率、机械效率和总效率(图6～8)。由图6可知,虽然马达的容积效率是随着行驶速度增加而增加,但其变化并不明显,而马达的容积效率随着系统压力的增大而减小。由图7可知,马达的机械效率是随着行驶速度增加而减小,其变化也相当显著,同时马达的机械效率随着系统压力的增大而增加。由图8可知,液压马达的总效率是随着系统压力的增大而增加。由此可知挖掘机在中低速档行进时,其液压马达处于比较高效的工作状态。

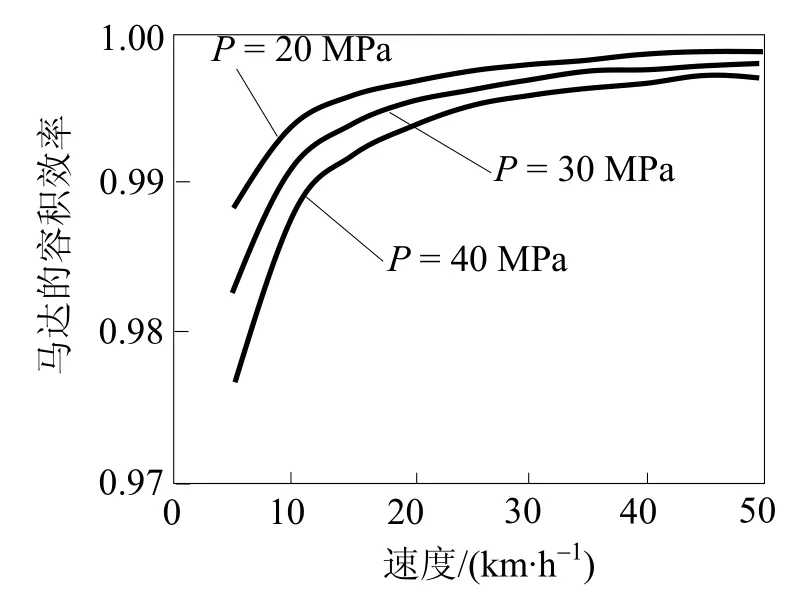
图6 A6VM马达q m=q m min=60.79 mL/r下行驶状态容积效率

图7 A6VM马达q m=q m min=60.79 mL/r下行驶状态机械效率

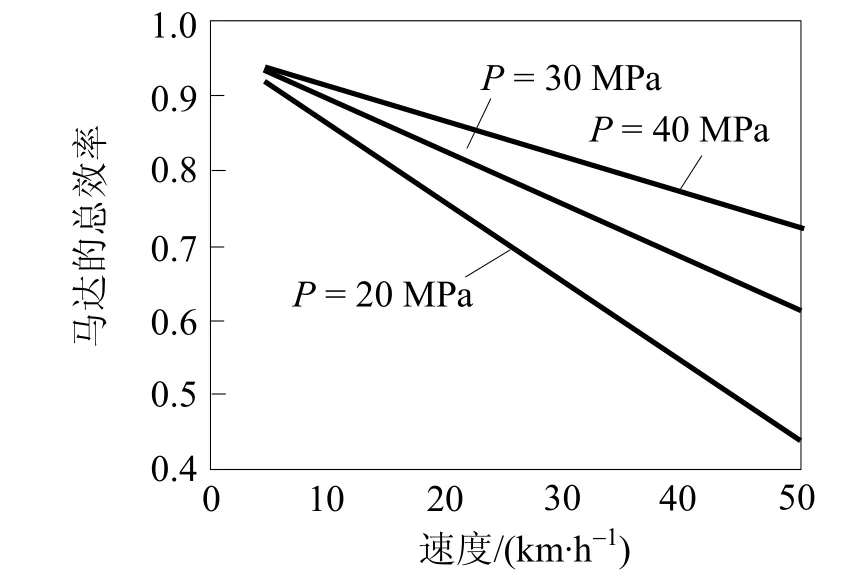
图8 A6VM马达q m=q m min=60.79 mL/r下行驶状态总效率

6 结论

以康明斯 C260-20作为挖掘机用发动机,根据液压系统元件的型号及匹配参数进行不停车换挡液压系统的参数计算,得到了泵的容积效率、机械效率和总效率在作业工况下随速度变化的曲线,通过曲线可知当轮式液压挖掘机的行驶速度高于10 km/h,液压泵会有比较高效的工作状态。经过对不同车速下马达的容积效率、机械效率和总效率图分析可知,总效率是随着系统压力的增大而增加,挖掘机在中低速档行进时,其液压马达处于比较高效的工作状态。

[1]王永奇.履带式智能全液压推土机关键技术研究[D].西安:长安大学,2008.

[2]姚怀新.工程机械底盘及其液压传动理论[M]．北京:人民交通出版社,2001.

[3]姚怀新.行走机械液压传动理论(连载7)[J].建筑机械,2003(2):58–60.

[4]陈永峰,陈杰荣.全液压平地机的动力匹配及牵引性能分析[J].建筑机械,2007(2):91–93.