基于旅游资源整合的高速公路网络双层规划模型及实例研究

□文/刘洋

基于旅游资源整合的高速公路网络双层规划模型及实例研究

□文/刘洋

随着旅游业的发展，人们对于旅游交通的需求和关注不断增加。将高速公路资源整合到旅游交通网络中，是当前高速公路网络规划的趋势和方向。基于此，文章从旅游资源整合的角度出发，建立了基于旅游资源的高速公路网络双层规划模型。然后研究了模型的求解方法，采用遗传算法并用Matlab编写了求解的算法程序。最后，给出高速公路网络规划的实例研究，论证了模型的可行性和合理性。

旅游资源；双层规划；遗传算法；高速公路；网络；模型

旅游交通作为旅游系统的重要组成部分，是区域旅游业发展的重要支撑和保障[1]，其服务质量和水平影响着游客的旅游决策、旅游目的地的选择以及旅游资源的开发建设，进而影响到区域的旅游开发。

高速公路作为社会经济发展到一定阶段的产物，具有缩短行程时间、节约花费、便捷舒适、安全等优点。随着居民生活水平的提高、私家车保有量的增长以及人们对出行路网环境需求的提升，将高速公路资源整合到旅游交通网络中，建立合理、高效、便捷的交通系统，是当前区域路网规划的趋势和方向，也是促进旅游景区的开发与资源整合的必然需求。实践证明旅游景点附近高速公路交通网络的建设，能使依靠公路交通运输的旅游风景区辐射半径扩大320～500km[2]。

近年来，公路网络优化的主要方法是实证调查、数理分析方法、系统分析、四阶段方法和网络设计问题（NDP）。网络设计问题是指在约束条件下选择最优的投资决策，通过新建路段或改扩建路段来使整个公路网络的性能达到最优，满足远期交通增长的需求[3～4]。网络设计中的决策变量不同决定了其模型也会不一样，决策变量主要有新建路段和改建路段提升能力两种，同时NDP也被分为3类：离散性、连续性和混合性，分别对应不同的决策变量[5]。由于双层规划能够充分解释网络设计问题的决策过程，因此Gwo-Hshiung Tzeng利用多目标数学规划来设计连续性网络设计模型，利用双层规划的思想解释并讨论带有多目标决策的网络改进问题，建立了非线性双层规划模型[6]。

在以往的省域高速公路网络规划时，一般只考虑主要城市的连通性，未将旅游景区的连通性纳入其中。随着旅游业的不断发展以及旅游景区服务需求的提高，高速旅游公路的规划将成为必然。

1　问题描述

在进行基于旅游资源的公路网络规划时，既要考虑到政府部门的规划决策，又要考虑到出行者的出行需求。从网络规划者（政府部门）的角度考虑，希望整个网络系统的出行总费用最少，同时，在将高速公路网与旅游资源整合时，希望规划后的路网旅游资源需求增加最大。从网络用户（出行者）的角度考虑，每个用户都希望出行的时间或者费用最少。综合考虑，为使模型建立更接近于真实情况，单一的优化目标不能满足此规划的要求，因此，本文采用双层规划模型，上层从网络规划者（政府部门）的角度考虑，下层规划模型从网络用户（出行者）的角度考虑。

2　模型建立

2.1优化目标

基于旅游资源的高速公路网络规划从微观分析入手，建立双层规划模型。上层模型的优化目标为整个网络系统的出行总费用（时间）最少，路网旅游资源需求增加最大。下层模型的优化目标为单个用户的出行费用（时间）最少。

其中路网旅游资源需求如何量化是目标函数的关键。通常计算旅游资源需求时，会将旅游景区的现有规模、开发规划、服务水平以及旅游者的消费水平等作为考虑因素，计算出的需求增加是由于旅游景区的开发等因素导致的。本文衡量的是规划路网建成后对于旅游资源需求的影响，可以通过交通量的增加来反映，在此提出旅游交通诱增量的概念。计算分析规划路网建成后由于路网结构的改善等而增加的旅游交通量。

在计算交通诱增量时，一般引用重力模型进行计算[7]。本文提出的旅游交通诱增量为交通诱增量的一个分支，因此重力模型也适用于旅游交通诱增量的计算。借鉴张航提出的基于重力模型预测交通量的方法[8]，给出旅游交通诱增量模型。

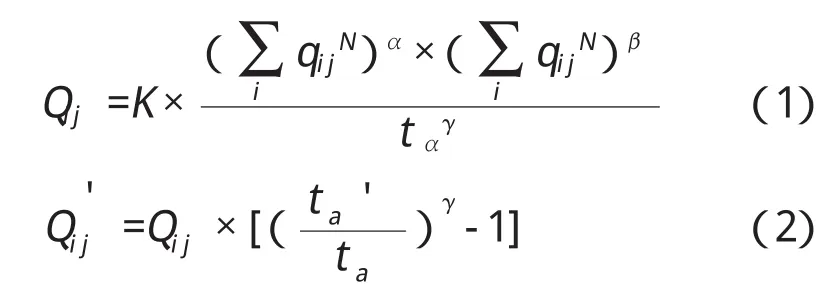
式中：qijN为i区到j区间的旅游交通出行量；Qij为i区到j区的旅游趋势交通量分布；Qij＇为i区到j区的旅游诱增交通量；tα为无此项目时（现状）i区到j区的交通阻抗；tα＇为有此项目时，i区到j区的交通阻抗；K、α、β、γ为重力模型参数。

2.2符号定义

其中，xα，ya，为决策变量，是0-1变量，xα为新建路段时，其值为1，否则为0；ya为扩建路段时，其值为1，否则为0。να（xα，ya）为路段a上的交通量，tα[να（xα，ya），xα，ya]为路段a上的出行时间；minz（xα，ya）为公路网的总出行时间；maxF（xα，ya）为基于旅游需求的总诱增交通量。

在约束条件中，需要考虑路网造价、规划里程、服务水平等约束。其中，m1为新建路段α的单车道造价，万元/km；m2为扩建路段α的造价，万元/km；M为预期建设资金的最大值，常数；lα为新建路段a的里程，km；lyy为规划前（即原有）公路网里程，km；L0为公路网规划总里程；ωα为规划路段α的服务水平，即V/C（路段交通量与路段通行能力之比）；ωmin为最小允许服务水平；ωmax为最大允许服务水平。

2.3双层规划模型形式

由上述可以建立公路网络路线布局的双层规划模型。

其中，优化目标（1）、（2）为上层优化目标函数，（1）表示基于旅游需求的总诱增交通量最大，（2）表示路网系统的总时间最少。优化目标（3）为下层优化目标函数，（3）表示单个用户出行时间最少。其实质是路网的平衡配流模型。本文采用Beckmannde用户平衡分配模型。此模型较为成熟并且应用颇多，在此不再赘述。

约束条件中（1）表示高速公路网络规模在最佳规模内；（2）表示路段服务水平（V/C）在一定范围内；（3）表示规划总投资在预期建设资金内；（4）表示交通流守恒；（5）表示路段流量守恒。

3　模型求解算法

3.1上层优化模型目标函数的转化

在本文上层优化模型中，有两个目标函数，应先转化为单目标函数。将多目标函数转化为单目标函数一般可采用加法或乘除法。本文中上层优化模型中的两个目标为基于旅游需求的总诱增交通量最大，路网系统的运行时间最小，两目标处于冲突状态。因此，本文适合用乘除法进行目标函数的转化，转化后的单目标函数为

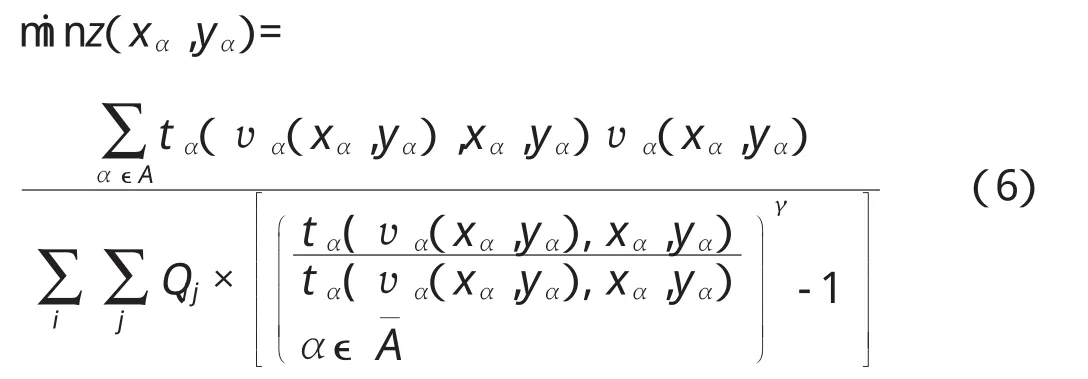
3.2遗传算法求解步骤

类似上述交通网络的双层规划模型常用的解法通常有Bender分解法、分枝定界法、极点算法、互补旋转算法、模拟退火算法以及一些启发式算法求解[9]。因为模型的上层和下层均为0-1混合整数规划问题，比较适合采用遗传算法进行求解。本文对遗传算法的求解步骤进行改进。

首先，进行交通流分配，计算各个体对应的目标函数值，对个体按目标函数值进行排序。将目标函数值不大于当前最优值的个体转入下层规划进行交通流分配，计算路段交通量和负荷度V/C。如果Gen＞GenMax或stop＞stopMax，结束计算；否则，Gen=Gen+1，根据交通流分配结果检查上层约束条件，将不满足条件的个体省去。然后，计算种群的个体适应度函数值，利用“无回放随机选择法”进行选择操作，依概率进行交叉、变异操作，交叉采用两点交叉操作，转向第1步。结束，输出结果，得到最终的路网优化方案。

其中，设置初始进化代数Gen=0，最优值维持步长stop=0；设置初始目标值Zmax为一相当大的正数，随机设定一个由初始可能连接图的子图构成的种群作为上层规划的初始方案。群体规模取10，交叉概率和变异概率分别取0.9和0.1，最大进化代数取100。利用Matlab软件及其提供的遗传算法工具箱编写程序。

4　算例分析

4.1方案描述

为更好地反映实际规划需求，本文给出了4个优化方案分别进行模型的求解，进行对比分析，选取最优的优化结果。

现阶段黑龙江省大部分旅游景区并未在高速公路网络节点内，即旅游景区与高速公路网络是不连通的，这会对模型的求解造成困难。因此，在设计方案之初，首先要连接一些旅游高速公路，从而保证路网的连通性。本文将5个旅游景区（亚布力、五大连池、杜尔伯特、镜泊湖、饶河县）纳入路网节点，除亚布力外，其他景区均与高速公路网络不连通，因此，需要在现有路网基础上增加4条旅游高速公路作为设计方案。

将高速公路网络与5个旅游景区连接可以有很多种方案，考虑到设计旅游高速公路线路的人为因素，仅做出一种设计方案进行路网优化的计算是不合理的、片面的。但由于篇幅的限制，本文不能给出所有旅游高速公路连接的可能性，在综合专家建议、选线合理性等情况的基础上，给出3个设计方案。依据上文提出的模型，将3个设计方案进行网络优化，选择出最优的路网优化方案。

同时，给出方案4作为基本方案，仅将15个主要城市作为路网节点，不考虑5个旅游景区的情况，与方案1～3进行对比分析。

4.2模型参数取值

根据黑龙江省《黑龙江省骨架路网规划》的公路远景规划，2020年公路建设总投资约600亿元，高速公路总里程将达到7000km。单位里程造价新建道路2 000万元/km，扩建道路800万元/km。上层模型中路段负荷度约束上限取为1，下限取0。

4.3数据信息

1）路网节点编码。将黑龙江省内的15个主要城市（包括地级市）与5个旅游景区进行编号，见表1。

表1　路网节点编码

2）网络距离矩阵。根据《黑龙江公路水路交通“十一·五”规划》和《黑龙江省骨架路网规划》以及专家意见，在现状公路网的基础上，给出每种方案的路网距离矩阵。矩阵中包括现有路段和备选路段，现有路段的距离为已知数据，备选路段的距离根据专家选线的方案得出。

3）小区划分及编码。为进行交通流分配，以各市政府所在地为形心，所管辖范围为小区范围，将路网划分为8个交通小区，见表2。

表2　黑龙江省OD小区编号

4）机动车OD矩阵。根据《黑龙江省骨架路网规划》及《黑龙江公路水路交通“十·一五”规划》中的公路运输量需求分析以及主要公路通道交通量预测结果进行反推，预测各节点交通生成量后进行交通分布，得到2020年各小区之间的机动车OD交换量的预测结果，见表3。但是由于调查方式及数据的局限性，所计算出的机动车OD交换量存在一定的误差，仅为此案例做以计算分析使用。

表3　黑龙江省高速公路网络机动车OD（百辆标准小汽车）

4.4模型优化结果

将所有的数据信息录入，运用M atl ab程序进行运算，得出4种方案的优化结果。将4种方案的优化结果进行对比分析，见表4。

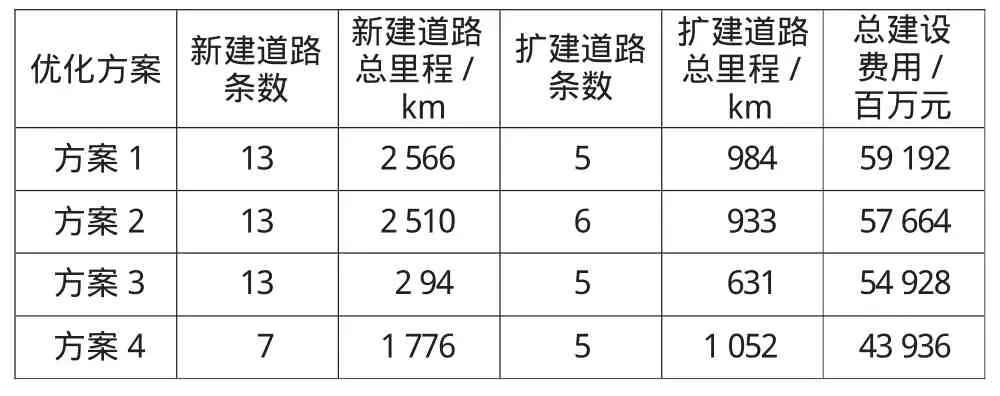
表4　4种优化方案结果比较

方案4的总建设费用较少，但是由于其只考虑了主要城市的连通性，而没有将主要旅游景区纳入其内，不能更好地发挥高速公路网在旅游资源优化上的优势，只作为对比方案使用，不能作为最优方案。

方案1、2、3均为纳入旅游景区为节点的高速公路网络优化，虽然总建设费用较多，但都在其约束条件的范围内。不仅能够满足整个路网总通行时间最小的优化目标，还能满足提高旅游诱增交通量的目标。方案1共新建了8条连接旅游景区的高速公路，分别为杜尔伯特—大庆，五大连池—杜尔伯特，五大连池—北安，饶河县—佳木斯，亚布力—佳木斯，饶河县—同江，亚布力—镜泊湖，镜泊湖—牡丹江。方案2共新建7条连接旅游景区的高速公路，分别为五大连池—北安，杜尔伯特—齐齐哈尔，镜泊湖—牡丹江，饶河县—佳木斯，五大连池—杜尔伯特，亚布力—佳木斯，亚布力—镜泊湖。方案3共新建8条连接旅游景区的高速公路，分别为五大连池—北安，杜尔伯特—大庆，镜泊湖—牡丹江，饶河县—同江，杜尔伯特—齐齐哈尔，五大连池—杜尔伯特，亚布力—佳木斯，亚布力—镜泊湖。方案3的总建设费用比方案2少27.36亿元，比方案1少42.64亿元，大大减少了投资费用。综合比较，选择方案3作为最终的优化方案。

5　结语

高速公路网络与旅游资源整合的发展策略将成为未来公路网规划的一个趋势和方向。本文建立了基于旅游资源的高速公路网络双层规化模型，采用遗传算法进行求解并用Matlab软件及其工具箱编写了算法程序。以黑龙江省高速公路网络优化作为实例分析，验证了模型的可行性。

[1]黄琳，金海龙，包瑞.新疆旅游交通现状及发展研究[J].新疆师范大学学报：自然科学版，2008，27（1）：103-106.

[2]欧越男，谢光秋.高速公路建设与发展旅游经济的可行性探讨[J].交通与运输，2005，（2）：60-62.

[3]Luis Gouveia，Jose Manuel Pires.Models for a Steinerringnetwork design Problem with revenues[J].EuroPeanJoumal of Operation Researeh.2001，(133)：21-31.

[4]Melkote Daskin M.S.An intenrated model of facility loeationand transportation network design [J].TransPortationResearch PartA.2001，35(6)：515-538.

[5]Johnson D.S，Lenstra J.K.and Rinnooy Kan A.H.G.The complexityof the network design Problem[J].Network.1978，（8）：279-285.

[6]Chen Y W，Tzeng G H.A fuzzy multi-objective model forreconstructing the post-quake road-network by geneticalgorithm[J].International Journal of Fuzzy Systems，1999，1(2)：85-95.

[7]王兵，董志宏，曹中杰.诱增交通量理论研究[J].河北工业大学学报，2002，31(6)：102-106.

[8]张航，张玲.基于重力模型预测诱增交通量方法研究[J].公路交通技术，2006，2(1)：111-113.

[9]雷英杰，张善文.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005.

□DOI编码：10.3969/j.issn.1008-3197.2015.01.027

□U491.1+2

□C

□1008-3197（2015）01-77-04

□2014-11-24

□刘洋/男，1980年出生，工程师，同济大学在职研究生，研究方向为建筑与土木工程。