全国大学生数学建模专科组赛题的系统研究

王积建，龚洪胜（浙江工贸职业技术学院 人文系，浙江温州325003）

全国大学生数学建模专科组赛题的系统研究

王积建，龚洪胜
（浙江工贸职业技术学院 人文系，浙江温州325003）

通过对1999—2014年的专科组赛题的系统研究，提炼了影响赛题质量的几个因素：实践性、综合性、社会影响、开放性、高等数学比例、解题难度，为数学建模竞赛的命题提出了若干建议。

数学建模；专科组赛题；命题；建议

0　引言

从教育部网站[1]可查得，2014年高职高专院校招生数318.4万人，占学生总数的45.5%，而本科院校招生数381.4万人，占学生总数的54.5%。虽然高职高专院校与本科院校的招生规模大致相当，但2015年高职高专院校参赛学生数却远远低于本科院校（仅占参赛学生总数的10.5%[2]。由于参赛学生是层层筛选而来，因此可以推断，参加数学建模普及教育的高职高专学生也占大学生总数的10.5%。换句话说，占学生总数45.5%的大学生，接受数学建模课程教育的学生仅有10.5%，比例严重失调！

从2014年全国大学生数学建模竞赛总结会议上获悉，2014年全国高职高专院校参赛数量有所下降，这引起了全国组委会的高度重视。尽管有各种各样的原因，但高职高专竞赛指导教师普遍认为专科组赛题太难，使得学生参赛不能获奖而下一年放弃。为什么不能获奖就放弃呢？这是因为，学校参赛需要领导审批，需要投入一定的成本，包括人力、物力、财力、时间等，如果参赛获奖了，表明投入有效益，领导有政绩，老师学生有成就感，下一年继续参赛；如果没有获奖，老师学生就失去了信心，甚至产生畏惧感，领导也不重视、不支持了，下一年放弃就成为可能。

好的赛题是竞赛成功的关键之一，这是全国组委会的一个基本认识[3]。对于专科组来说，命题工作出现两难局面。一方面不能太简单，如果简单到连微积分或线性代数都考不到，那就成为中学生竞赛了，不能叫做大学生竞赛了；另一方面，又不能太难，题目的难度究竟控制在多高，很难确定。因此，如何针对专科组提出一个好赛题成为亟待解决的问题。

本文通过对1999—2010年赛题综合评价和对1999—2014年赛题赛后研究，对今后专科组赛题的命题工作提出一些思考和建议。

1　基于对1999—2010年赛题综合评价的赛题分析

什么样的赛题才是好赛题？俗话说，金杯银杯不如老百姓的口碑，金奖银奖不如老百姓的夸奖。2011年，在全国大学生数学建模竞赛成功举办20周年之际，受全国大学生数学建模竞赛组委会委托，由陈笑缘教授领衔的研究团队采用调查研究方法，对1999—2010年专科组的24个赛题的质量进行了综合评价和分析，下面对研究过程和结果进行简述。

1.1对1999—2010年赛题综合评价综述

研究团队通过征求命题专家和数学建模指导教师，建立了赛题质量综合评价指标体系，包括7个一级指标和20个二级指标，如表1所示[4]。

表1　赛题质量评价指标体系及权重

关于指标的相对重要性，使用问卷调查的方法收集数据，调查对象是全国组委会和浙江省组委会专家，回收有效问卷32份。使用基于0～1规划的群模糊层次分析法[5]获得了指标权重，如表1所示。在7个一级指标中，重要性从大到小排序为：实践性>综合性>基础性>挑战性>开放性>社会影响>科研推动。实践性和综合性比较重要，体现了数学建模课程意义所在，即它是联系数学与实际问题的桥梁。

关于指标打分，也使用问卷调查的方法收集数据，调查对象是全国大学生数学建模竞赛指导老师、参赛学生和数学建模资深专家。回收有效问卷82份(包括学生问卷36份)。使用模糊综合评价法对赛题质量进行了评价[1]，结果如表2第3、4列所示。接着使用费谢尔最优分割法将24个赛题进行了分类[6]，结果如表2第5～7列所示。

表2　所有24个赛题的综合评价及分类

1.2对“好赛题”的选取

从表2可知，赛题“对学生宿舍设计方案的评价”、“饮酒驾车”和“易拉罐形状和尺寸的最优设计”获得了较高的质量评价。

尽管综合评价方法很多，尽管不同的评价方法会得出不同的结果，但不管采取什么方法，最优对象和最劣对象的排名往往变化不大，比较稳定。因此，排名前3的赛题应该是老百姓公认的“好赛题”，而不随评价方法的变化而变化。

2　基于对1999—2014年赛题赛后研究的赛题分析

上一节主要从赛题的功能属性方面对各个赛题进行了个体分析，本节从求解赛题需要使用的知识分布及解题难度方面对专科组赛题进行整体分析而不是作个体分析。

从2012年开始，全国组委会倡导和鼓励广大竞赛指导教师开展“赛后继续研究”，笔者响应这一号召，将1999—2013年的30个专科组赛题进行了系统研究，出版了专著《全国大学生数学建模竞赛试题研究（1999—2013）》（上下册）[7]，具备了对各个赛题客观准确的评价能力，下面进行评价分析。

2.1评价维度

由于研究目的是分析求解赛题究竟需要多少中等、高等数学知识，以及解题难度大小，故选择2个维度，第一维度是中等数学与高等数学，第二维度是知识数量和解题难度。

2.2知识数量的打分方法

求解赛题需要的知识（或方法）数量如何界定？笔者是从获奖的全国优秀学生论文、公开发表的教师论文、以及笔者专著里，筛选出正确的、尽可能简单的知识和方法作为打分依据，而不是以知识高深、方法新颖、思路独特等标准为依据的。另外，中等数学和高等数学的数量多少是相对而言的，故以比例形式为数量多少的打分结果。

中等数学与高等数学的数量多少赋值方法如表3所示。

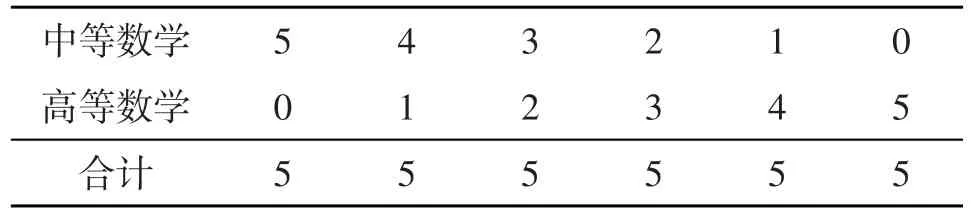
表3　知识数量比例的赋值方法

这里需要说明的是，高等数学知识的比例分量为0，是指使用中等数学知识就可以成功解题，而不是不能使用高等数学知识解题。事实上，如果使用高等数学知识也可以成功解题。

针对每个赛题的知识数量的打分方法，以赛题“古塔的变形”问题（1）为例，举例说明如下。

“古塔的变形”问题（1）：给出确定古塔各层中心位置的通用方法，并列表给出各次测量的古塔各层中心坐标。

问题（1）需要的知识主要有空间平面方程知识，最小二乘拟合方法和重心法，这些知识全部属于高等数学的范围，故中等数学知识数量的比例分量赋值0，高等数学知识数量的比例分量赋值5，即中等数学与高等数学的知识数量的比例为0:5。

2.3解题难度的打分方法

解题难度包括数学知识本身的难度、计算机编程难度、数据处理难度等。举3个例子分别说明。

例1极坐标比直角坐标难度大。因为直角坐标比极坐标常用，故学生对直角坐标的熟练程度较高，故直角坐标的难度较低，极坐标的难度较高。

例2完全自编程序比有现成的计算机求解命令难度大。

例3大数据比正常数据难度大。近年来大数据进入数学建模赛题中，比如赛题“公共自行车服务系统”，里面含有20天的、181个站点的、每天24小时的用车记录，仅第20天就有4万多条记录，从这海量数据中进行统计分析，难度一定很大了。

难度划分3档：难、中、易，分别赋值3、2、1。特别地，如果知识数量为0，则难度也为0。

中等数学和高等数学的难度评价是独立的，而不是相对的，即中等数学（比如极坐标）的难度如果最大，就赋值3，而高等数学（比如随机数学）的难度如果也最大，也赋值3。

针对每个赛题解题难度的打分方法，仍然以赛题“古塔的变形”问题（1）为例，举例说明：重心公式属于物理学知识，里面包含了行列式，空间平面方程属于空间解析几何知识，拟合空间平面方程需要计算机编程（但数据量不大），综合衡量这些知识的难度，属于最大等级，故赋值3，而中等数学知识数量可以忽略不计，其难度自然就赋值0。

2.4打分结果

所有赛题的知识数量及解题难度赋值结果，如表4所示。

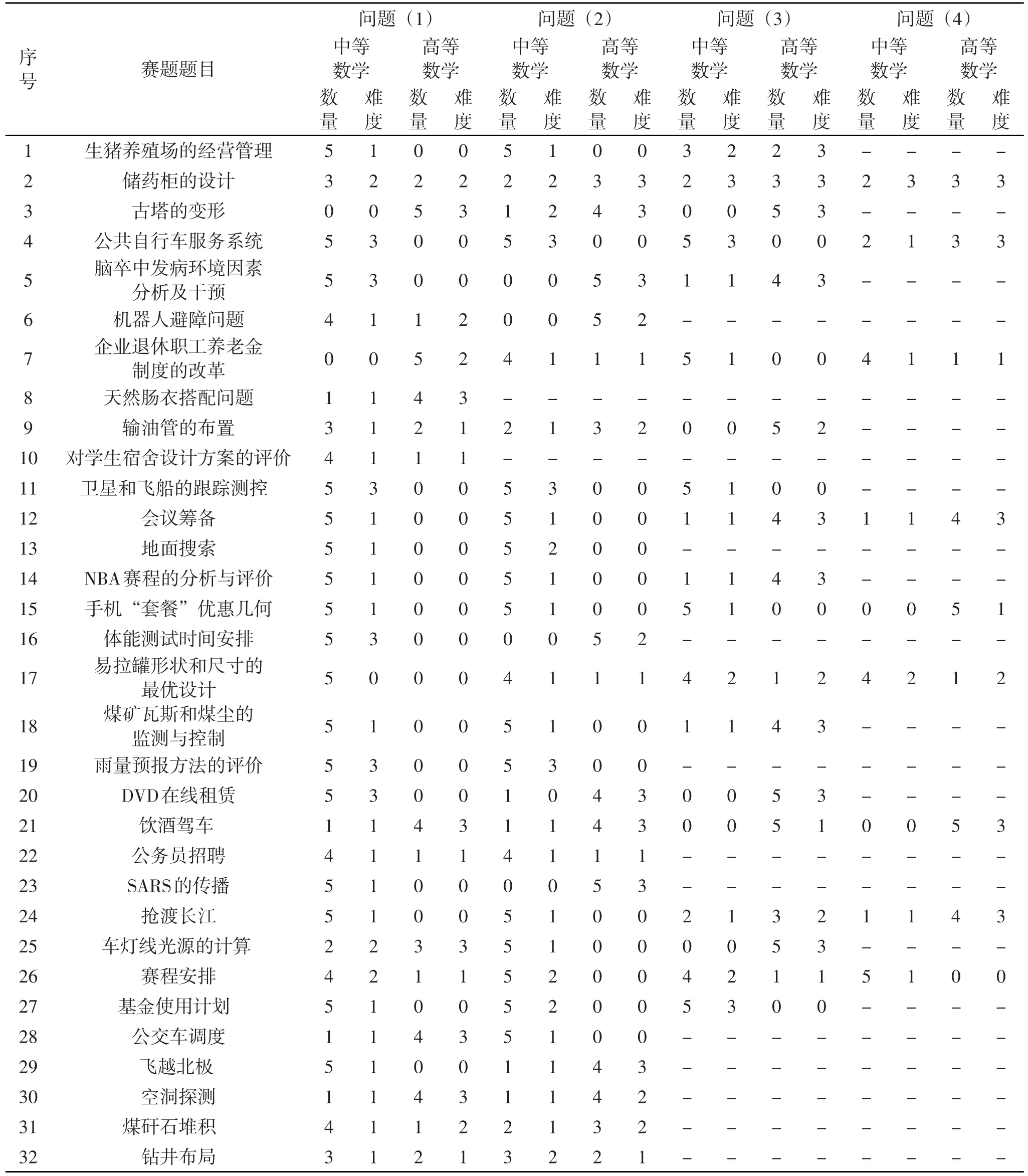
表4　1999—2014年专科组赛题的打分结果

2.5统计分析

2.5.1描述分析

所有32个赛题，一共有90个小题，将中等数学、高等数学的知识数量汇总，再按照每个小题平均，得到中等数学与高等数学的数量比例约为3: 2，因此高等数学的知识数量低于中等数学的数量。

将中等数学、高等数学的难度（剔除0）汇总，再按照每个小题平均，得到中等数学难度约为1.5，高等数学的难度约为2.3，表明中等数学的难度是中等偏下，而高等数学的难度是中等偏上，这个结论与目前广大教师普遍反映的赛题难度较大的事实相符。

2.5.2方差分析

为了比较中高等数学的知识数量、解题难度的差异是否显著，使用单因素方差分析方法[8]，结果显示，在知识数量上二者有显著差异（p=0.0000< 0.01），即中等数学显著地多于高等数学。在知识难度上二者无显著差异（p=0.6890>0.05）。

2.5.3趋势分析

为了比较中高等数学在知识数量上或解题难度上随时间的变化趋势，画图，如图1和图2所示。解题难度方面的平均值取中等数学和高等数学的算术平均值。

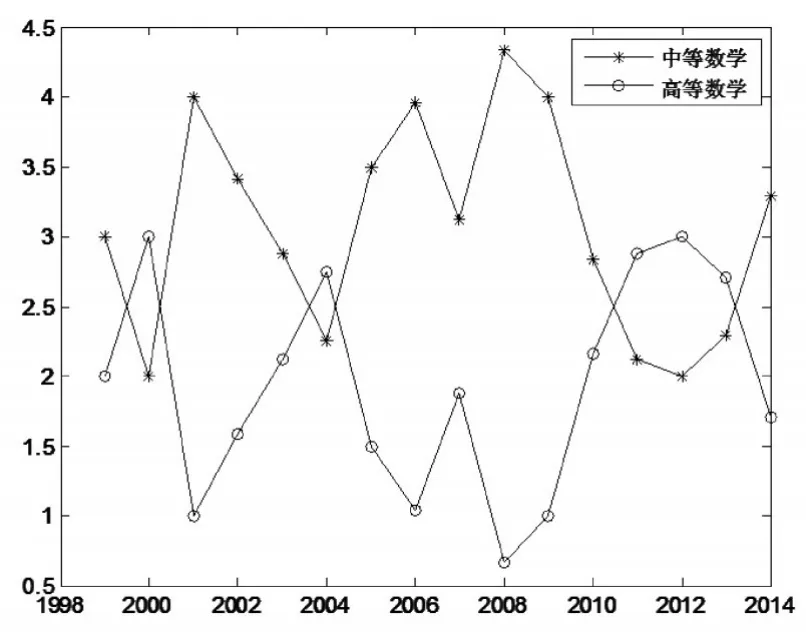
图1　知识数量随时间的变化趋势

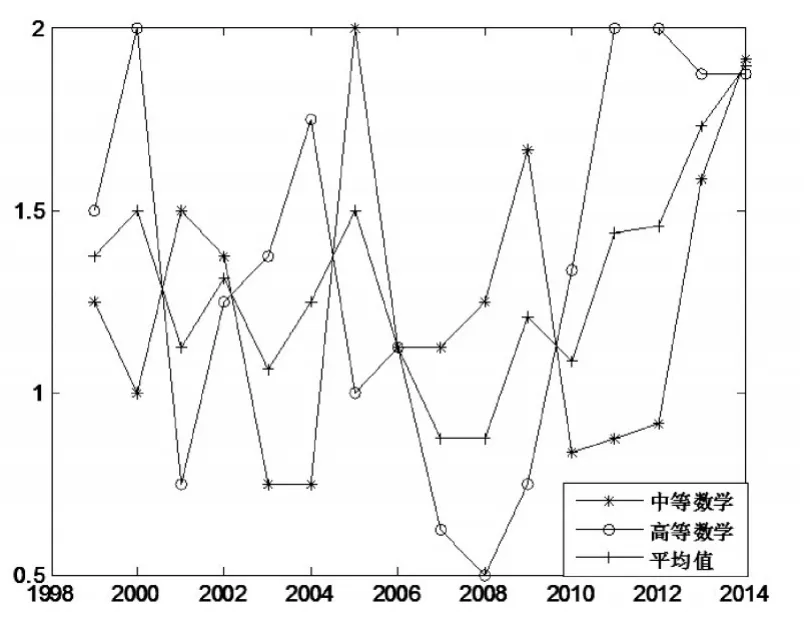
图2　解题难度随时间的变化趋势

从图1可得出以下结论：

（1）高等数学知识数量只有在2000、2004、2011、2012、2013年这5个年份高于中等数学。

（2）从2008—2012年，高等数学知识比重逐年增加，这与高职院校指导教师普遍认为赛题偏难的事实一致。

（3）2013、2014年的高等数学知识数量有所降低，说明命题专家有意识的降低了高等数学知识的比重。

从图2可得出以下结论：

（1）从2007—2014年，解题平均难度呈现上升趋势（2010年较上年有所下降），这与高职院校指导教师普遍认为赛题偏难的事实一致。

（2）从2012—2014年，高等数学的难度逐年下降，说明命题专家有意识的降低高等数学的解题难度。

（3）从2010—2014年的中等数学难度逐年提高。

综上所述，全国组委会命题专家组在高等数学的知识比重和难度方面控制得比较到位，使得数学建模竞赛能够成功举办20多年。当然，高等数学的比重是否更低一些，解题难度是否更小一些，这些都值得命题专家深入思考。

3　对“好赛题”的特征分析

针对第1节选取的3个好赛题作具体分析，这3个赛题的知识分布及解题难度如表5所示。

下面对这3个“好赛题”作具体分析。

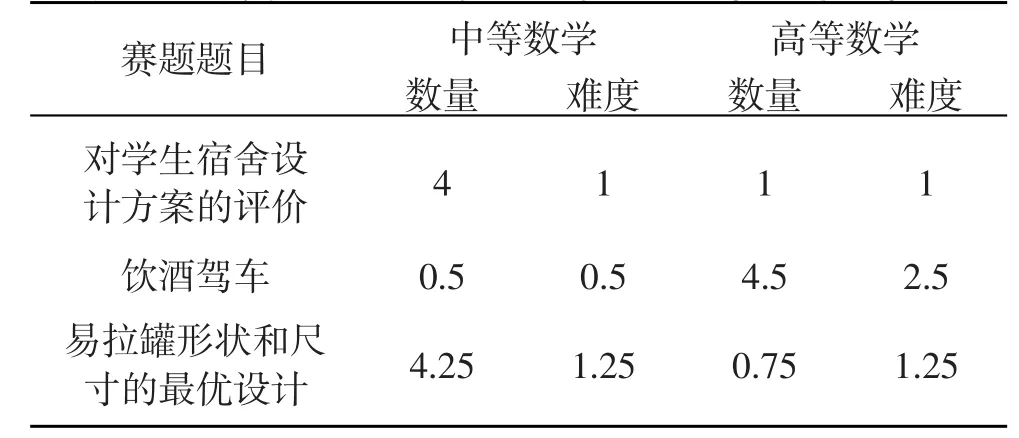
表5　“好赛题”平均每小题的知识分布及解题难度

3.1“对学生宿舍设计方案的评价”的特征分析该题目具有以下特点：

（1）从题材上贴近学生。该题目是关于学生宿舍设计方案的综合评价问题，由于学生对自己住宿的宿舍楼非常熟悉，如同熟悉自己的家庭房屋一样，具有非同寻常的亲切感，宿舍楼的设计图纸也很直观，直接就能看懂，不存在陌生的概念、抽象的术语、专业名词等，所以学生几乎遇不到任何理解上的障碍。

（2）从知识数量上贴近学生。该题目是一个综合评价问题，求解时，需要建立评价指标体系（含定义各个指标），确定各个方案各个指标的指标值并进行极性一致化和无量纲化处理，确定指标权重、选择评价方法（有逼近理想解法、层次分析法、加权求和法），所有这些工作，除了层次分析法含有矩阵知识外，其余工作都只需要中等数学知识就够了，故中等数学与高等数学的比例为4:1。

（3）从解题难度上贴近学生。对于中等数学来说，从知识方面、编程方面、数据规模方面，难度均较小，故赋值1。对于高等数学来说，层次分析法里需要定义成对比较矩阵，这容易理解，编程计算也不难，数据规模很小，虽然读图纸搜集数据花费时间较多，但难度不大，故难度赋值1。因此，求解该题目的总体难度较小，学生能够驾驭，跳一跳够得着。

3.2“饮酒驾车”的特征

该题目具有以下特点：

（1）具有很强的实践性。饮酒驾车，甚至醉酒驾车是危害交通安全的重要因素，全社会（包括参赛学生）都知晓饮酒驾车这一现象，对于题目的几个问题（司机体内酒精浓度检测、酒后多长时间内驾车就会违反标准、怎样估计血液中的酒精含量在什么时间最高、如果天天喝酒是否还能开车），都是实际中存在的现实问题，解决这些问题具有十分重要的应用价值，故赛题的实践性评价结果很高。

（2）具有很强的综合性。解决该题目需要用到生物知识、化学知识、微分方程知识，以及列方程、求最值、求极限等微积分知识，还要使用计算机画函数图像，所以赛题的综合性评价结果很高。

（3）具有很强的基础性。题目叙述清楚明白，一读就懂，每个小问题很容易转化为数学问题，例如，对于怎样估计血液中的酒精含量在什么时间最高的问题，显然就是求函数最大值问题。此外，用到的高等数学知识非常多，除列方程是中等数学知识之外，其余几乎全部是高等数学知识，故平均每个小题中等数学与高等数学的知识比例为4.5:0.5。

（4）具有很强的社会影响。饮酒驾车在2004年是社会关注的热点问题，电视、报刊等媒体经常报道此类新闻，交警也加大了酒驾查处力度，所以该题目在社会影响指标上具有较高的评价分值。

3.3“易拉罐形状和尺寸的最优设计”的特征

该题目与赛题“对学生宿舍设计方案的评价”类似，也具有以下特点：

（1）从题材上贴近学生。该题目是关于易拉罐形状和尺寸的最优设计问题，由于学生对可口可乐、雪碧等易拉罐饮料非常熟悉，所以与赛题“对学生宿舍设计方案的评价”类似，学生不存在题意理解上的障碍。

（2）从知识数量上贴近学生。该题目第2小题需要使用圆柱体体积和表面积公式建立一个一元函数，然后转化为求一元函数的最小值问题，就可以确定决策变量的尺寸。接下来的几个问题解决思路是相同的，只不过要使用圆台体积公式和侧面积公式，目标函数和约束条件更复杂了，模型也由无约束优化模型变成了非线性规划模型，故平均每个小题中等数学与高等数学的知识比例为4.25:0.75。

（3）从解题难度上贴近学生。该题目的第1小题是测量问题，对于动手能力较强的高职高专学生来说，这简直就是他们的拿手好戏。后面的几个题目，使用立体几何公式建立目标函数和约束条件也不难，而计算机编程也有现成的求解命令，故平均每个小题中等数学与高等数学的难度系数均为1.25。

4　对今后命题的建议

通过以上对“好赛题”的评价分析，提出几条数学建模命题时需要重点考虑的因素，供命题专家组参考。

（1）实践性。相比其它课程，培养学生的实践能力在数学建模课程目标中具有十分突出的地位，所以实践性和应用性是数学建模课程的核心目标。与此相适应，数学建模赛题的实践性应该得到强化，赛题必须来源于真实的实际情景，而不是人为编制的。同时，赛题研究结果能够返回到实际中去，研究结果或结论能够直接应用于实际并能解决实际问题，或者指导实践，或者被有关部门采纳。实践性越强表明赛题质量越高。

（2）综合性。赛题既然来源于实际，就应该从物理、化学、生物、医学、材料、信息、环境、经济、金融、能源、体育、教育等某个领域提炼出来，涉及的领域相对宽泛一些较好，综合性越强表明赛题质量越高。例如，赛题“脑卒中发病环境因素分析及干预”，涉及了数学、统计、医学、气候环境等领域，综合性强，是个好赛题。

（3）社会影响。某个时期被社会强烈关注的问题，承载了社会大众的期望，也具有一定的光环效应，这些问题本身蕴藏着较高的、现实的研究价值，对于扩大数学建模竞赛的社会影响具有十分显著的作用，因此，赛题应该聚焦于社会影响大的素材，社会影响越大表明赛题质量越高。例如，近年来我国载人航天飞船的成功发射影响巨大，鼓舞人心，因此赛题“卫星和飞船的跟踪测控”具有较高的社会影响，是个好赛题。

（4）开放性。赛题的开放性是指解题信息开放程度、解题方法多样性、研究结果多样性、后续研究的拓展性等。好的赛题应该具有较大的开放性和自由度，给全国大学生提供一个广泛思考和充分发挥才能的空间，开放性越强表明赛题质量越高。例如，赛题“企业退休职工养老金制度的改革”，其后续研究的问题很多，给参赛学生在赛后申报校级学生科研项目打下了很好的基础，是个好赛题。

（5）高等数学比例。对于专科组赛题来说，并不是高等数学比例越大越好，适度降低高等数学比例，同时增加中等数学比例，可以提高高职高专学生的学习积极性，提振参赛信心。例如，赛题“公共自行车服务系统”，中等数学比例就很大，高等数学比例很小，甚至于全部使用中等数学知识和方法也可以完成。

（6）解题难度。对于专科组赛题来说，并不是难度越大越好，也不是越小越好，毕竟这是竞赛。适度降低难度，以适应当前高职高专院校数学课程被压缩的现实状况，同时也有助于扩大高校的参赛率和学生受益面。例如，赛题“地面搜索”，高等数学比例为0，自然高等数学难度也为0，而中等数学的难度也不大，平均每小题的难度系数为1.5，相对来说比较容易。

[1]2013年教育统计数据·全国基本情况[EB/OL].中华人民共和国教育部网站,[2015-7-2].http://www.moe.gov.cn/publicfiles/business/htmlfiles/moe/s8493/index.html.

[2]谢金星.2013年总结[J].工程数学学报,2013,30(增刊一):1-2.

[3]“全国大学生数学建模竞赛”征题通知[EB/OL].全国大学生数学建模竞赛网站,[2015-7-2].http://www.mcm.edu.cn/html_cn/ block/7d929fc8a4090b9cfbc6687f047bd81c.html.

[4]陈笑缘,王积建,邢益冰.历届全国大学生数学建模竞赛专科组试题的模糊综合评价[J].数学的实践与认识,2012,42(21):50-57.

[5]王积建.基于0-1规划的群模糊层次分析法[J].模糊系统与数学,2015,29(1):117-125.

[6]王积建,陈笑缘,茹永梅.历届全国大学生数学建模竞赛专科组试题的最优分类[J].深圳职业技术学院学报,2013(1):38-43.

[7]王积建.全国大学生数学建模竞赛试题研究[M].北京:国防科技大学出版社,2015.

[8]陈再余,陶应虎.统计学原理与实务[M].北京:清华大学出版社,2009.

（责任编辑：尹清杰）

ASystematic Research on the Topics(College Group)of National University Students Mathematic Modeling Contest

WANG Ji-jian,GONG Hong-sheng
(Humanities Department of Zhejiang Industry＆Trade Vocational College,Wenzhou,325003,China)

Based on a systematic research on the topics of National University Students Mathematic Modeling Contest from 1999 to 2014,several factors are identified as an impact on the quality of topics including practicality,comprehensiveness,social impact,open-mindedness,relatedness of advanced mathematics and the degree of difficulty of the topics.We have also made some suggestions for the selection of topic.

mathematical modeling;college contest topic;topic selection;suggestion

O14

A

1672-0105(2015)04-0013-07

10.3969/j.issn.1672-0105.2015.04.004

2015-10-15

王积建，硕士，浙江工贸职业技术学院副教授，主要研究方向：数学建模及其教育；龚洪胜，浙江工贸职业技术学院讲师，主要研究方向：应用数学。