车辆悬挂功率反馈主动控制算法
2015-12-05张进秋毕占东王兴野
张 磊,张进秋,毕占东,何 旭,王兴野
(装甲兵工程学院 装备试用与培训大队,北京 100072)
车辆悬挂功率反馈主动控制算法
张 磊,张进秋,毕占东,何 旭,王兴野
(装甲兵工程学院 装备试用与培训大队,北京 100072)
以提高车辆减振性能为目的,提出一种基于降低悬挂系统传递至车体平均功率的功率反馈主动控制算法。以某轮式车辆四分之一车辆二自由度悬挂系统模型为研究对象,基于时域和频域相结合的方法对算法性能进行分析和评价,并分析权重系数取值对算法性能的影响。结果表明:功率反馈控制算法能够显著改善车辆的乘坐舒适性和操纵稳定性,提高车辆减振性能。
振动与波;悬挂系统;主动控制算法;功率反馈
悬挂是车辆的重要组成部分,弹性连接车体和车轮,衰减车辆运行过程中由于不平路面激励传递至车体的振动。研究表明,悬挂性能对车辆的乘坐舒适性、操纵稳定性等行驶相关的重要特性有直接影响[1,2]。目前,绝大部分车辆仍采用被动悬挂,其悬挂参数不可调,难以适应复杂行驶路面环境的需求。基于主动、半主动控制的可控悬挂是提高悬挂性能的公认有效途径。其中,主动悬挂性能最优,是车辆可控悬挂技术的发展方向,而行之有效的控制算法一直是主动悬挂设计和开发的关键问题。
关于可控悬挂控制算法的研究几乎涵盖了所有先进的控制理论和控制方法,一些成熟的算法,如天棚控制[3]、最优控制[4]、鲁棒控制[5]、模糊控制[6]以及神经网络控制[7]的性能都已得到分析和验证。近年来,一些学者基于能量流分析的方法探索悬挂系统输入到车体的平均功率对车辆减振性能的影响,得到的结论是通过降低输入到车体的平均功率有助于提高车辆的减振性能[8,9],但设计的算法是一种频域最优控制模型,需要实时获取路面的输入频率,无法工程实现。
本文以提高车辆的减振性能为目标,基于降低悬挂系统输入到车体的平均功率的考虑,提出适用于车辆悬挂的功率反馈主动控制算法,并以被动悬挂和天棚主动悬挂为参照,对该算法性能进行分析和评价。
1 悬挂系统动力学模型及分析
四分之一车二自由度悬挂系统模型相对简单,且能够较为真实地反映车辆垂直方向的基本振动特性,常用作悬挂系统概念设计、控制算法验证的基础[1],故本文基于该模型进行主动控制算法设计和性能分析。
对于采用独立悬挂的车辆,假设其质量分配系数为1,且仅考虑垂直运动方向的振动,可建立如图1所示的1/4车二自由度主动悬挂系统动力学模型。假设坐标原点选在各自平衡位置,则主动悬挂系统的力学方程为
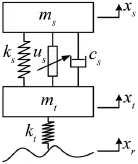
图1 主动悬挂系统动力学模型
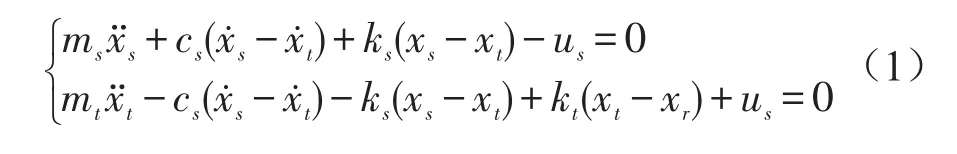
式中ms和mt分别为车体和车轮的质量;ks和kt分别为悬挂弹簧和车轮的刚度;cs为悬挂系统阻尼系数;xs、xt和xr分别为车体、车轮的垂直位移和路面不平度激励;us为主动控制力。
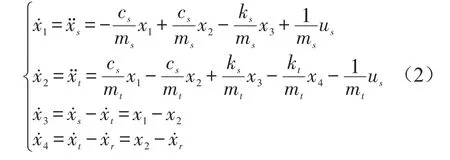
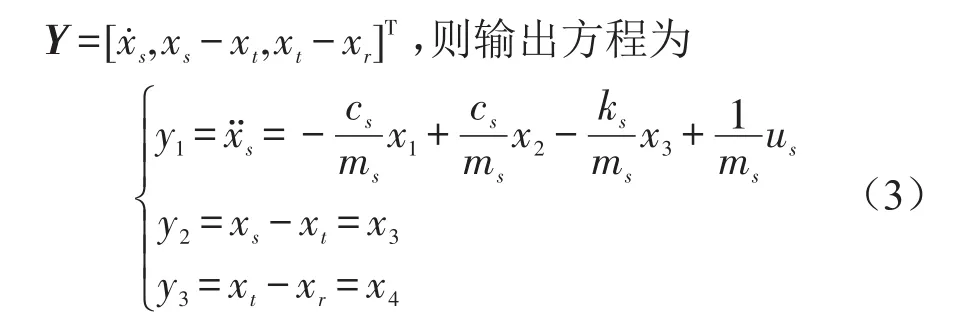
取U=us为控制变量、干扰,则悬挂主动控制系统状态方程式可表示为
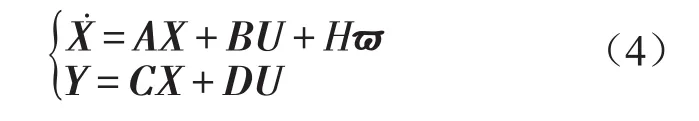
式中
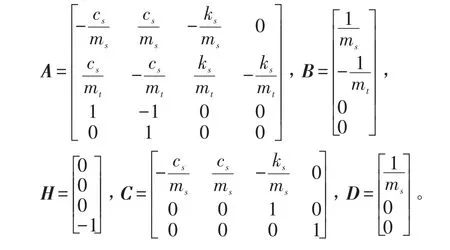
2 控制算法设计
功率是作用于系统某一点的力与速度的乘积。对于振动控制系统,它综合考虑了力和速度对系统的影响。振动控制领域的功率流理论常用平均功率反映系统输入功率的大小,即
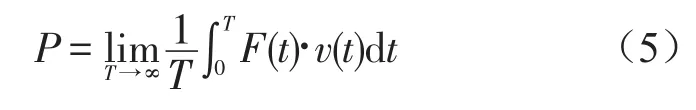
式中F(t)作用于系统的外力,v(t)为系统产生的速度响应。
对于悬挂系统振动模型,以车体为研究对象,它受到的合外力为悬挂弹簧、阻尼器及作动器对车体作用力的合力,由式(1)得
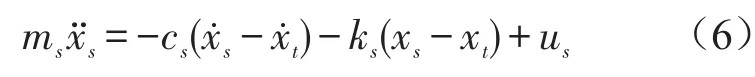
则悬挂系统输入到车体的功率为

本文算法设计以传递至车身的功率最小为控制目标,提出车辆悬挂功率反馈(Power Feedback,简称PF)控制算法,并基于最优控制理论实现并分析该算法。
以减小悬挂输入到车体的功率为控制目标,以作动器出力为约束条件,建立性能泛函
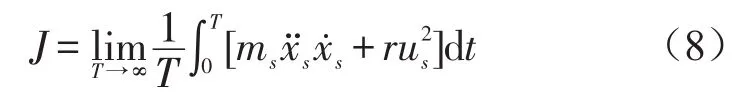
式中控制目标的权重系数取1,r为约束条件的权重系数。由于算法中控制目标和约束条件各只有一个,避免了复杂的权重系数取值多目标优化问题。
将式(8)中的状态变量和控制变量通过状态方程的形式表示出来,即
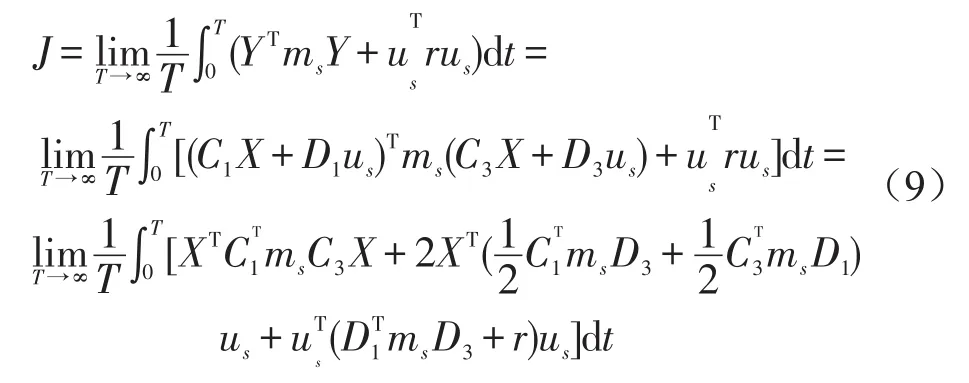
式中Ci、Di分别为状态矩阵C、D的第i行。

因而根据任意时刻t的状态反馈变量X,就可以求出该时刻作动器的最优控制力
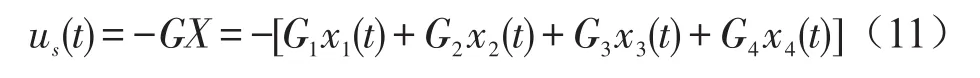
显然,PF主动控制算法是一种以限制车体输入功率为目标的全状态反馈控制,其中车轮动变形的状态一般难以直接测量,工程中可以采用状态预估的方式获取,最常用的方法是基于Kalman滤波器进行预估,具体方式此处不再赘述。
3 性能分析与评价
为分析功率PF控制算法的有效性,采用车辆悬挂振动控制领域常用的天棚主动控制算法为对比,基于Matlab/Simulink分别建立被动悬挂、天棚(Skyhook,简称SH)主动悬挂和PF主动悬挂系统动力学模型,从时域和频域的角度对算法性能进行分析评价。其中,对应式(1)所示动力学模型的SH主动控制算法,其控制力为

式中csky为天棚阻尼系数。
以某型轮式车辆为研究对象,被动悬挂系统参数如表1所示。其中,被动悬挂的车轮静变形为0.019 m,假设悬挂许用动行程为±0.1 m。
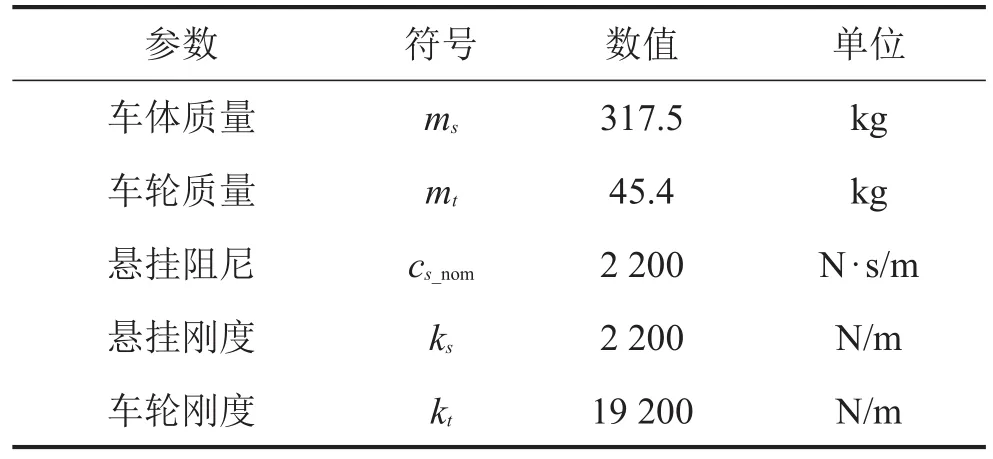
表1 被动悬挂系统悬挂参数
SH主动控制算法中,通常情况下csky取值越大,车辆的乘坐舒适性和操纵稳定性越好,故本文取较大的天棚阻尼系数csky=2 cs_nom=3 000 N·s/m,记作SH主动悬挂;对于PF主动控制算法,为分析权重系数取值对悬挂减振性能的影响,分别取两组不同权重系数r1=3×10-14,r2=1×10-14,记作PF1和PF2悬挂。
3.1 时域分析
时域分析对确定激励和随机激励两方面进行响应分析。其中,确定激励通过三角冲击来考察悬挂的高频振动行为,主要考察指标为车体加速度;随机激励用于对悬挂性能进行综合分析。
(1)三角冲击
假设车辆以2 m/s的速度进行直线行驶,在t=0.5 s时通过高度为5 cm、宽度为20 cm的三角形减速带,4种悬挂的车体加速度时域曲线如图2所示。
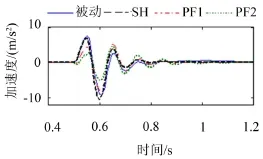
图2 三角波冲击响应
由图2可知,与被动悬挂相比,SH主动控制对车体加速度降低效果十分有限,而PF1控制和PF2控制却能有效抑制加速度峰值,且PF2控制作用最佳,但一定程度导致了越过障碍后的加速度小幅波动时间变长。在0.4 s~1.2 s范围内,不同悬挂的车体加速度峰值、均方根值如2表所示。

表2 三角波冲击车体加速度响应
(2)随机激励
基于谐波叠加法[10]分别生成车速为20 m/s时C级路面激励和车速为10 m/s时的D级路面激励,分析不同悬挂在随机激励下各指标的响应。
由于篇幅限制,只给出C级路面下车体加速度、悬挂动行程和车轮动变形的时域曲线,如图3所示。为直观起见,本文仅给出了仿真10 s~12 s时长的悬挂各指标时域曲线,整个仿真时段的控制效果对比将通过数据统计的方式进行分析。
计算可得不同行驶工况下三个指标的均方根值和峰值如表3所示。其中,PF1和PF2控制相比于被动悬挂和SH主动悬挂均可大幅降低车体加速度均方根值和峰值,但导致悬挂动行程和车轮动变形峰值和均方根值一定程度增大;PF2对加速度的控制效果优于PF1,但PF2控制下悬挂动行程和车轮动变形增大程度也大于PF1,说明减小权重系数r的取值有助于提高乘坐舒适性,却一定程度增大了悬挂动行程和车轮动变形,但两种行驶工况下PF1和PF2控制的悬挂动行程均在许用范围,并未导致“悬挂击穿”,D级路面条件下PF2的车轮动变形的峰值明显大于静变形,说明该工况下偶尔会出现车轮离地现象。受悬挂固有特性的限制,悬挂各指标之间存在一定约束关系,理论上难以通过控制使悬挂动行程和车轮动变形同时减小。
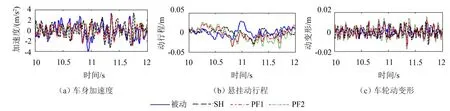
图3 悬挂各指标时域曲线
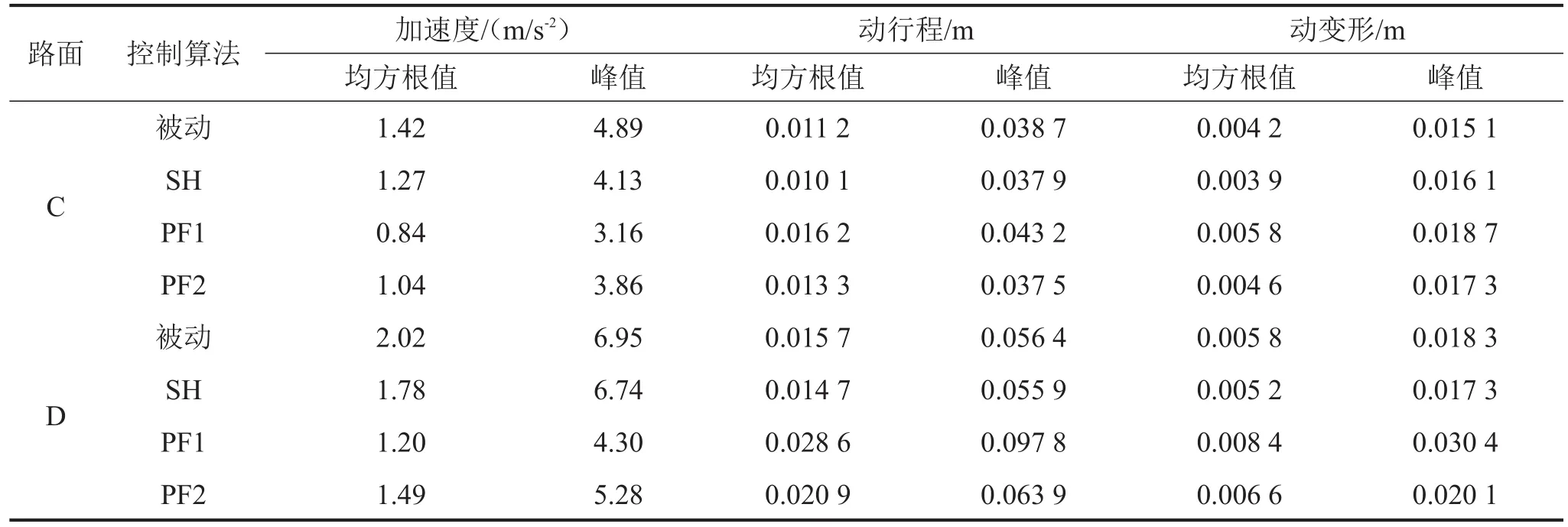
表3 悬挂各指标均方根值和峰值计算结果
3.2 频域分析
悬挂系统各指标时域统计结果带有一定随机性,要全面分析控制算法性能,还需进一步通过频域分析。不同控制条件悬挂系统各指标传递率如图4所示。由图4(a)可知,在路面激励频率低于车轮共振频率时,PF控制可以大幅降低车体加速度,且权重系数r取值越小,车体加速度降低程度越大;在路面激励频率大于车轮共振频率时,PF控制对加速度的抑制作用有限,且随r取值的减小,在高频区有小幅的控制恶化趋势,但不明显;相比之下,SH主动悬挂只能在车体共振区对车体加速度实现有效抑制,其控制效果和有效频域范围明显不及PF控制。由此印证了PF主动控制对车体加速度的抑制效果。
从车辆隔振的角度,悬挂动行程并非越小越好,只需将其限制在设计范围内,降低发生“悬挂击穿”的概率即可[11]。“悬挂击穿”主要发生在振幅较大的低频区,特别车体共振区。由图4(b),PF控制和SH控制均能够明显降低车轮共振区悬挂动行程的传递率,一定程度降低了发生悬挂击穿的概率,但PF控制导致车轮共振区悬挂动行程有一定程度增大。
由图4(c),在车轮共振区之前的频段,PF控制较被动悬挂可有效降低车轮动变形传递率,其效果优于SH主动控制;PF控制对车轮动变形的降低幅度随权重系数r的减小而增大;在车轮共振区,PF控制导致车轮动变形传递率有所增大,且随r的减小动变形传递率的增大幅度趋于明显。
3.3 性能评价
控制算法性能评价主要考虑算法性能对车辆乘坐舒适性和操纵稳定性的影响。目前,车辆乘坐舒适性评价广泛采用ISO法,该方法以车体加权加速度均方根值为指标;操纵稳定性评价指标通常采用车轮动变形均方根值。上述评价方法存在的不足表现在评价结果受路面状况和车速等车辆运行工况影响显著;此外,通过计算动变形均方根值的方法评价操纵稳定性,没有考虑路面激励的频域差别。
针对上述不足,文献[12]中分别定义了车辆乘坐舒适性和操纵稳定性评价函数,该函数以无控制时的标准被动悬挂为对比,通过传递函数频域加权积分的方法对受算法影响的悬挂性能进行评价,提高了悬挂性能评价的有效性。
乘坐舒适性评价函数定义为
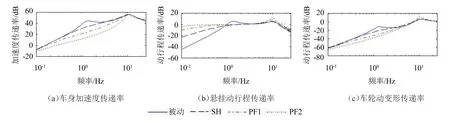
图4 悬挂传递率分析
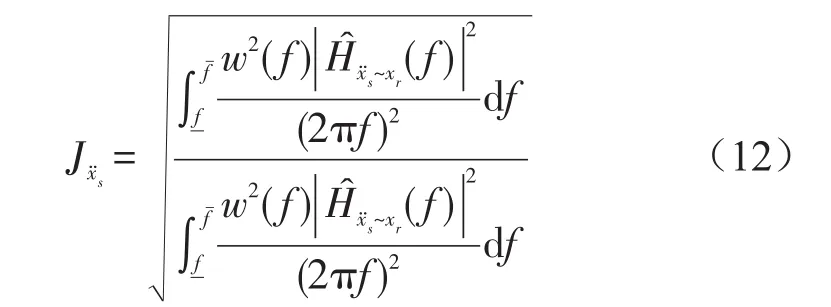
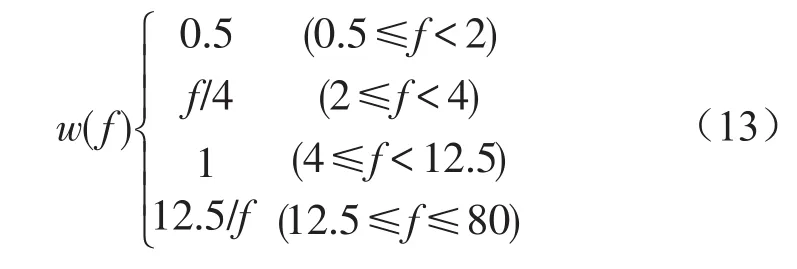
文献[12]认为,车轮动变形对操纵稳定性的影响具有频率差别:当路面激励频率较低时,动变形处于低谷持续时间较长,对操纵稳定性影响较大;随着路面激励频率的升高,动变形低谷持续时间逐渐变短,对操纵稳定性的影响也越来越小。所以操纵稳定性评价函数定义为
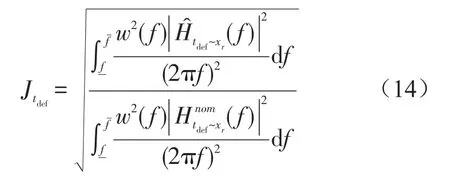
基于上述方法对被动悬挂以及SH、PF1、PF2控制下的主动悬挂性能进行评价和对比,所取频率范围为0.5 Hz~25 Hz,该频率范围可反映出车体、车轮受悬挂性能影响产生振动的主要动力学特征,其结果如图6所示。可见,与被动悬挂相比,SH主动控制可使车辆乘坐舒适性提高8.11%,操纵稳定性提高33.32%;PF1控制可使车辆乘坐舒适性提高16.81%,操纵稳定性提高50.49%;在PF2控制下,车辆乘坐舒适性和操纵稳定性分别提高了33.96%和48.86%。评价结果表明,PF控制下悬挂系统的减振性能总体优于SH主动悬挂;PF主动控制算法中,较小的权重系数取值有助于显著改善车辆乘坐舒适性,而对操纵稳定性的改善程度与权重系数取值较大时相差不多。
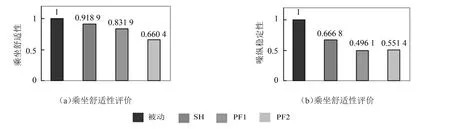
图6 悬挂性能评价结果
4 结语
为改善车辆的减振性能,提出一种基于降低悬挂系统输入至车体平均功率的功率反馈主动控制算法。以被动悬挂和天棚主动悬挂为对比对算法性能进行了分析和评价,得到如下结论:
(1)功率反馈主动控制算法能够在车轮共振区以下的频段有效降低车体加速度和车轮动变形,显著改善车辆的乘坐舒适性和操纵稳定性;并较好地抑制了车身共振区的悬挂动行程,一定程度降低了发生“悬挂击穿”的概率,其总体减振效果明显优于天棚主动悬挂。
(2)功率反馈主动控制算法的权重系数取值对算法性能有较大影响。较小的权重系数有助于提高车辆乘坐舒适性,而对操纵稳定性影响不大。实际应用中,应根据控制目标合理选择权重系数。
笔者认为,基于功率分析进行悬挂系统控制算法设计是一种有效的思路和方法,该方法控制目标明确,物理意义清晰,有较大的研究空间。
[1]俞凡,于秀敏.汽车系统动力学[M].北京:机械工业出版社,2008.
[2]董小闵,余淼,廖昌荣,等.汽车磁流变半主动悬架频域加权次优控制研究[J].系统仿真学报,2006,18(11):3183-3186.
[3]Karnopp D,Crosby M J,Harwood R A.Vibration control using semi-active force generators[J].ASME Journal of Engineering for Industry,1974,5(2):619-629.
[4]Ercan Y.Optimal control of half-car vehicle model with a variable damping semi-active suspension[C].Proceedings 10 th Int.Conf.on ER&MR,2006:431-437.
[5]Chen H,Liu Z-y,Sun P-y.Application of constrained h∞control to active suspension systems on half-car models [J].Journal of Dynamic Systems,2005,127(3):245-254.
[6]颜文俊,董丹,王维锐,等.非线性半主动悬架系统模糊控制策略[J].控制工程,2011,18(6):941-946.
[7]王春华,唐焱.车辆主动悬架的BP神经网络自适应PID控制[J].计算机仿真,2009,26(5):274-277.
[8]陈昆山,戴建军,胡思明.基于功率流方法电磁反力混合型主动悬架研究[J].噪声与振动控制,2008,28(5):21-24.
[9]刘丽丽.车辆主动悬架系统的功率流传递特性及最优控制策略[D].青岛:山东科技大学,2004.
[10]段虎明,石峰,谢飞,等.路面不平度研究综述[J].振动与冲击,2009,28(9):95-101.
[11]Gang Wang.Constant Force Control Methodology for Shock Absorption.US Patent Application[J].US 2010/ 0332079A1,2010.
[12]彭志召,张进秋,张雨,等.车辆半主动悬挂的频域控制算法[J].装甲兵工程学院学报,2013,27(4):36-42.
Power FeedbackActive ControlAlgorithm for Vehicle’s Suspensions
ZHANG Lei,ZHANG Jin-qiu,BI Zhan-dong,HE Xu,Wang Xing-ye
(Brigade of Equipment Trial and Training,Academy ofArmored Forces Engineering, Beijing 100072,China)
In order to improve vehicle’s shock absorbing property,a power feedback active control algorithm based on the reduction of the average power transferring from suspension systems to vehicle’s body was put forward.The dynamic model of a quarter of the vehicle with a two-DOF suspension was chosen as a research object,and the performance of the control algorithm was analyzed and evaluated in time-domain and frequency-domain.The results show that the power feedback active control can obviously improve riding comfort,handling stability and shock absorbing property of the vehicles.
vibration and wave;suspensions system;active control algorithm;power feedback
U436.33
A
10.3969/j.issn.1006-1335.2015.03.028
1006-1355(2015)03-0130-05+148
2014-12-01
张进秋(1963-),男,博士,教授,博士生导师,主要从事车辆工程、智能材料研制与应用等方面研究工作。E-mail:zhangjq63@163.com
