响应面在磁悬浮轴承转子模型修正中的应用
2015-12-05徐园平
赵 晨,周 瑾,徐园平
(南京航空航天大学 机电学院,南京 210016)
响应面在磁悬浮轴承转子模型修正中的应用
赵 晨,周 瑾,徐园平
(南京航空航天大学 机电学院,南京 210016)
精确的磁悬浮轴承转子有限元模型对转子动态特性的研究及控制器的设计有着重要的作用。对于磁悬浮轴承转子的硅钢片圈、传感器基准环和光轴的过盈配合,有限元模型采用简化处理,使得转子弯曲刚度产生误差。为了获得精确的磁悬浮轴承转子有限元模型,需要利用响应面代理模型对有限元模型进行修正。以一个磁悬浮轴承转子为例,以模态频率和振型相关系数(MAC)为目标建立响应面,对转子的有限元模型进行修正。建立的响应面精度很高,修正后的有限元模型分析的模态频率、振型向量和试验值基本一致。结果表明,应用基于响应面的磁悬浮轴承转子模型修正方法修正过的有限元模型更加精确。
振动与波;磁悬浮轴承;模型修正;响应面;转子;振型相关系数
磁悬浮轴承转子的光轴上热套有硅钢片、传感器基准环等其他部件,改变了转子自身的弯曲刚度,使得有限元模型增添了许多不确定性因素。需要利用模型修正方法对磁悬浮轴承转子有限元模型进行修正。根据模型修正过程中使用实验数据的不同,模型修正方法可以分为基于频响函数的模型修正方法和基于模态参数的模型修正方法[1-3]两大类。
国内外对有限元模型修正方法已经进行了多方面的研究。Friswell[4-6]对基于模态参数的有限元模型修正方法的修正参数的选择、修正中的阻尼等进行了深入研究,得出了依据试验模态频率和模态振型共同修正有限元模型会更加准确的结论。在众多学者研究的过程中,响应面法[7,8]逐渐广泛运用于有限元模型修正及其工程应用中。该方法将有限元模型修正[9-10]的适用范围进一步推广到其他非线性领域。郭勤涛[11]研究了如何获得高阶高精度响应面及其对有限元模型修正精度的影响。宗周红[12]利用响应面代理模型对下白石大桥的有限元模型进行修正,模型修正后有限元分析结果与试验结果比较吻合。
有限元模型对于一些复杂转子结构的螺栓连接部分、过盈配合、轴承支承等的准确模拟,一直是一个研究的难题。针对磁悬浮轴承转子的硅钢片圈、传感器基准环和光轴之间的过盈配合,本文采用响应面法对磁悬浮轴承转子三个配合部分进行物理参数的识别,从而达到对转子有限元模型修正的目的。
1 响应面法的转子有限元模型修正的基本理论
1.1 响应面试验设计
试验设计方法[13,14]采用D-最优设计生成试验设计样本点。因为D-最优试验设计既可以保证精度也可以减少试验次数。磁悬浮轴承转子系统如图1所示,由转子、径向AMB、轴向AMB、传感器和控制器组成,转子的结构尺寸如图2所示。

图1 磁悬浮轴承转子系统
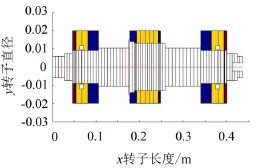
图2 磁悬浮轴承转子结构图(x转子长度;y转子直径)
转子的质量及几何尺寸都可以通过精确的测量工具获得。但对于转子轴段的一些刚度属性却很难确定。选取硅钢片和传感器基准环部分所在的轴段材料的杨氏模量作为修正参数。左右两个轴承支承轴段的结构尺寸是相同的,因此将支承轴段的杨氏模量E1和电机轴段的杨氏模量E2设为修正参数。
1.2 响应面的拟合
本文采用多项式回归法[15]建立响应面模型,用最少的试验代价取得最好的结果,快速而有效。磁悬浮轴承转子中自变量E1、E2与因变量Yi(i=1,2,3)之间的线性关系为
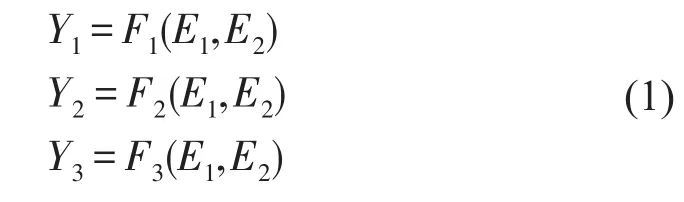
其中E1和E2是支承轴段和电机轴段的杨氏模量,Yi(i=1,2,3)代表前3阶弯曲模态频率或振型相关系数,Fi(E1,E2)(i=1,2,3)代表因变量Y和自变量E1和E2之间的多项式关系。利用D-最优设计生成实验设计样本点则生成杨氏模量的试验点如下式所示
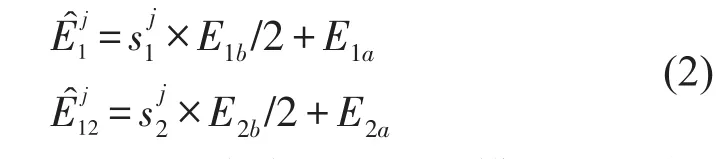
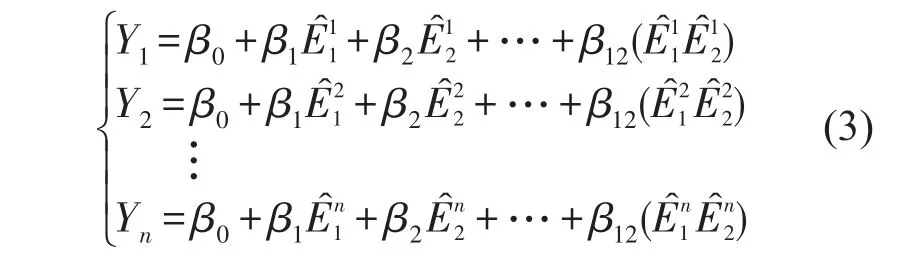
采用5阶多项式拟合试验点,Yi(i=1,2,…,n)为由有限元模型计算的模态参数(模态频率或振型相关系数),具体形式为

βi(i=1,2,…12)为多项式的系数。分别建立模态频率多项式响应面和MAC值多项式响应面。通常用误差平方R2、相对均分根误差RMSE作为检验响应面的精度。有限元模型修正过程中,不能仅以模态频率作为目标响应变量,同样需要考虑振型向量的匹配度。
1.3 基于响应面法的模型修正方法
建立的有限元模型和实际模型有一定差别,所以需要进一步进行模型修正,模型修正问题可以表述为以下的优化问题
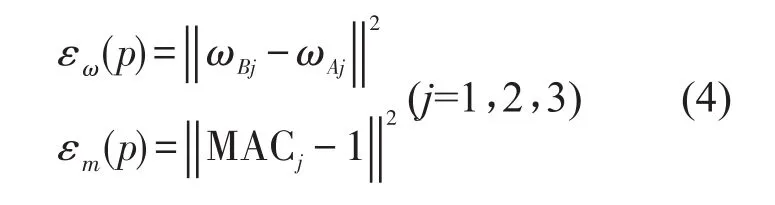
其中ωBj为响应面代理模型分析的模态频率,ωAj析为试验模态频率,MAC为响应面代理模型计算的前3阶弯曲模态振型和试验振型相关系数。εω(p)为响应面分析的模态频率和试验模态频率残差向量,εω(p)为MAC值和1的残差值。
上式中R为残差项,p表示设计参数,Kω(j)和Km(j)为对应的权重因子,pU和pL分别表示设计参数P的上限与下限。通过优化算法使残差项R最小的设计参数p即为最优参数值。
2 响应面代理模型对转子有限元模型的修正
2.1 模态实验
首先进行模态试验获得转子的模态参数,转子总长为436 mm,转子重量2.4 kg,光轴密度为7 850 kg/m3,光轴杨氏模量为206 GPa,转子支承位置的直径为39.8 mm。试验设备为OROS多通道信号分析仪、PCB力锤和ICP传感器,振动测点采用线状分布,边界为自由—自由。采用跑点锤击法采集频响函数,平均次数为5,采用模态分析软件识别模态参数。
2.2 磁悬浮轴承转子有限元模型修正
文中磁悬浮轴承转子实际工作转速一般在第1阶弯曲模态频率以下,选取转子前3阶弯曲模态参数作为目标响应量,对支承轴段和电机轴段的杨氏模量E1、E2进行修正。响应面的建立和有限元模型修正的过程如图3所示。

图3 转子模型响应面建立过程
用多元线性回归拟合,建立转子的前3阶模态频率关于修正参数E1和E2的响应面模型如图4所示。
响应面建立完成后,需要对响应面精度进行检验,采用R2和RMS E的准则检验模态频率和修正参数所建立的响应面,检验结果如表1。
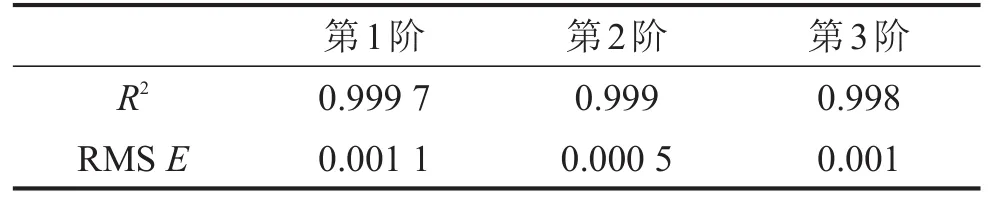
表1 模态频率和修正参数的响应面检验精度
振型相关系数(MAC)在90%以上,即认为有限元模型和试验模型之间存在很好的相关性。建立转子的前3阶弯曲模态MAC值关于修正参数E1和E2的响应面模型。同样,采用R2和RMS E的准则检验MAC和修正参数所建立的响应面,检验结果如表2所示。
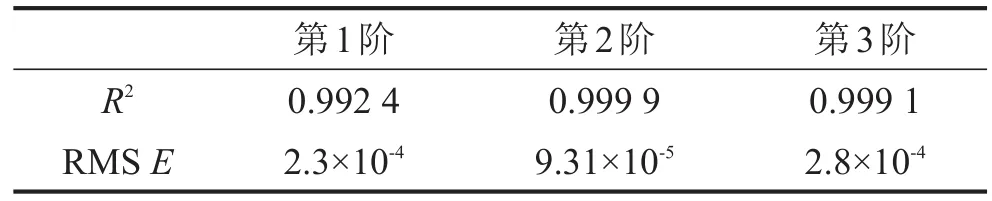
表2 MAC和修正参数的响应面检验精度
从检验结果表1和表2看出,模态频率响应面R2均在0.9以上,说明响应面模型的频率值与真值的总体差异很小;RMS E均小于1%,这说明响应面模型与真值的差别是平均幅值的1%。所以响应面模型精度很高,可以作为有限元模型的代理模型。修正参数E1和E2的修正前后值如表3所示。

表3 修正前后参数值对比
表4给出了修正前后模态频率误差对比,可以看出修正后有限元模型模态频率与试验值相比误差变得很小,表5给出了修正前后的MAC值,修正前后仿真振型和试验振型匹配度都很好,且修正后第2阶和第3阶精度有一定的提高。

表4 修正前后模态频率误差对比
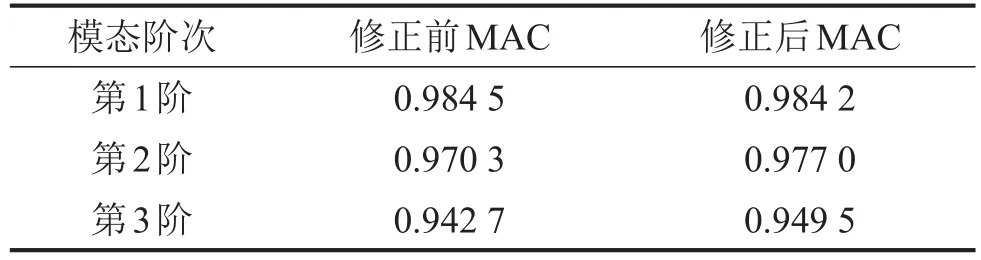
表5 修正前后前3阶模态振型相关系数对比
结合表4和表5可以看出,修正后的有限元模型更接近于真实模型,说明基于响应面法的磁悬浮轴承转子模型修正方法修正后的有限元模型更精确。
3 结语
基于响应面的模型修正方法结合模态试验数据修正的有限元模型精度较高,能够满足工程实际和试验研究需求。文中模态试验试件为磁悬浮轴承转子,模态试验数据为模态频率和振型相关系数(MAC)。磁悬浮轴承转子在光轴上热套有硅钢片、传感器基准环等其他部件,所以,转子有限元模型中有很多的不确定性,依据试验数据对有限元模型进行修正,可以提高有限元模型的精度。下一步可对磁悬浮轴承转子进行不确定性建模,当确定转子的物理参数分布后,可计算出有限元模型的动态响应范围,在磁悬浮轴承转子可靠性设计和振动分析阶段,具有重要的工程价值。
[1]Mottershead J E.Model updating in structural dynamics:A survey[J].Journal of Sound and Vibration,1993,167(2):347-375.
[2]Hu S L J,LI Hua-jun,WANG Shu-qing.Cross-model cross-mode method for model updating[J].Mechanical Systems and Signal Processing,2007,21:1690-1703.
[3]Bakir P G,Reynders E.An improved finite element model updating method by the global optimization technique Coupled Local Minimizes[J]. Computers and Structures,2008,86(11):1339-1355.
[4]Friswell M I,Mottershead J E,Ahmadian H.Combining subsetselection and parameterconstrantsin model updating[J].Journal of Vibration and Acoustics,1998, 120(4):854-859.
[5]Friswell M I,Garvey S D,Penny J E T.The convergence of the iterated IRS method[J].Journal of Sound and Vibration,1998,211(1):123-132.
[6]Friswell M I,Inman D J,Pikey D F.The direct updating of damping and stiffness matrices[J].American Institute of Aeronautics and Astronautics Journal,1998,36(3):491-493.
[7]邱飞力,张立民,张卫华,等.基于响应面方法的支架结构模型修正研究[J].噪声与振动控制,2014,34(3):139-143.
[8]张伟杰,陆秋海,缑百勇,等.基于逆响应面法的有限元模型修正[J].噪声与振动控制,2013,33(6):5-10.
[9]周星德,明宝华,潘瑞鸿,等.基于遗传算法的降阶模型修正方法研究[J].振动、测试与诊断,2007,27(1):25-28.
[10]Fei Qingguo,Li Ai qun,Miao Changqing.Dynamic finite element model updating using meta-model and genetic algorithm[J].Journal of Southeast University,2006,22(2):213-217.
[11]郭勤涛,张令弥,费庆国.用于确定性计算仿真的响应面法及其试验设计研究[J].航空学报,2006,27(1):55-61.
[12]宗周红,高铭霖,夏樟华.基于健康监测的连续刚构桥有限元模型确认(I)-基于响应面法的有限元模型修正[J].土木工程学报,2011,44(2):90-98.
[13]费庆国,张令弥,李爱群.基于统计分析技术的有限元模型修正研究[J].振动与冲击,2005,24(3):23-26.
[14]童恒庆.理论计量经济学[M].北京:科学出版社,2005:30-84.
[15]窦毅芳,刘飞,张为华.响应面建模方法的比较分析[J].工程设计学报,2007,14(5):359-363.
Finite Element Model Updating of the Rotor Supported by Magnetic Bearings Using Response Surface
ZHAO Chen,ZHOU Jin,XU Yuan-ping
(College of Mechanical and Electrical Engineering,Nanjing University ofAeronautics andAstronautics, Nanjing 210016,China)
Finite element model of the rotor supported by active magnetic bearings(AMBs)plays an important role in the dynamic characteristic analysis of rotor-bearing systems and optimal design of controllers.However,since the connections among the silicon steel coil,the sensor’s reference ring and the sleeve are simplified in finite element modeling, the rotor bending stiffness may include remarkable errors.To obtain an accurate finite element model of the magnetic bearing-rotor system,the response surface representative model is necessary to update the finite element model.In this paper,the response surface of a magnetic bearing-rotor system was established to update the finite element model of the rotor.The modal frequencies and Modal Assurance Criterion(MAC)were determined through the simulation.The results were compared with those of experimental measurements.It is found that the modal frequencies and the modal vectors are in good agreement with those of the experiments,and the finite element model of the rotor-AMB system updated by the response surface is more accurate than the conventional finite element model.
vibration and wave;active magnetic bearing;model updating;response surface;rotor;modal assurance criterion
TH133
A
10.3969/j.issn.1006-1335.2015.03.023
1006-1355(2015)03-0108-04
2014-12-17
江苏省自然科学基金(BK2011070);国家自然科学基金(51275240)
赵晨,江苏淮安人,硕士,目前从事磁悬浮轴承转子动力学方面研究。E-mail:zhao_chen05@163.com
周瑾,江苏徐州人,博士生导师。E-mail:zhj@nuaa.edu.cn
