基于神经网络方法的高速列车车外气动噪声预测

李 辉，肖新标，金学松

(1.西南交通大学 牵引动力国家重点实验室，成都 610031；2.西南交通大学 材料先进技术教育部重点实验室，成都 610031)

基于神经网络方法的高速列车车外气动噪声预测

李 辉，肖新标，金学松

(1.西南交通大学 牵引动力国家重点实验室，成都 610031；2.西南交通大学 材料先进技术教育部重点实验室，成都 610031)

利用神经网络进行高速列车车外气动噪声预测研究。基于Lighthill声学类比理论，建立高速列车气动噪声计算模型。在此基础上采用Levenberg-Marquardt(LM)算法建立车外气动噪声的神经网络预测模型，选取车外气动噪声样本点对预测模型进行训练，用训练好的神经网络预测模型预测车外气动噪声。结果表明，建立的神经网络模型对车外噪声具有较好的预测效果，可以用来进行高速列车车外噪声预测。

声学；高速列车；气动噪声；声类比理论；神经网络；预测

列车高速运行时，来自轨道、气流的激扰，使得整个铁路耦合大系统始终不会保持安静。比较常见的声源有轮轨噪声，气动噪声。高速列车体积较大，高速列车上的声源比较分散，甚至，整个高速列车都可看作是一个大的气动声源。目前，很难利用已有的方法将不同类型声源引起的噪声进行分离。同时，高速列成引起的噪声在车外近场、远场的分布规律无论从现场实验测试还是仿真上都难以进行整体把握。本文建立了一种可以对车外气动噪声进行预测的神经网络模型。在保证一定准确度与较小计算代价的基础上，弄清高速列车气动噪声对车外区域的影响。

国内外学者对高速列成气动噪声进行了大量的研究，文献[1]通过求解广义的Lighthill方程，给出了适合计算车辆行驶工况下的产生的气动噪声的方法。文献[2,3]介绍了高速列车上的主要气动声源，并对一些关键部位的噪声产生机理做了简要分析。文献[4]针对高速列车气动噪声的特点，对采用直接瞬态计算方法计算气动噪声的可行性进行了探讨，并指出高速列车头车、中车、尾车的引起的气动噪声属于宽频噪声。文献[5]对高速列车车头气动噪声进行了研究，分析了头部控制线形状对高速列车气动噪声的影响。文献[6,7]分析了高速列车车身表面的气动噪声源分布，表明列车气动噪声主要由车身表面脉动压力导致。

神经网络作为一种智能工具，也广泛运用在机械、电子、医疗卫生、信息等领域的系统识别，故障诊断，结果预测，参数优化等方面[8－14]。文献[8]利用神经网络进行了电动汽车用的磷酸铁锂电池荷电状态的预测研究，文献[9]用BP神经网络算法模型对人体血液红细胞浓度进行无创检测。文献[10]利用神经网络分析了各变形工艺参数对TB8合金固溶处理显微组织的影响规律。文献[11]利用神经网络方法较好地解决了现有磁悬浮球位置控制算法控制精度不高的难题，文献[12，13]利用神经网络进行轨道与齿轮箱的故障诊断。文献[14]利用神经网络进行了系统参数的优化。神经网络以其良好的非线性、容错性、任意逼近多输入输出参数函数和较好的鲁棒特性的优点[8]，在工程应用上取得了较好的效果。本文建立一种BP神经网络预测模型，预测高速列车速度为300 km/h时车外气动噪声，验证神经网络对噪声预测的精确性与适用性。

1 高速列车气动噪声模型

1.1 列车模型

列车中间车身截面形状变化不大，离开车头表面一定距离后，车身表面的气动压力变化不大。为了缩短计算时间，将八节编组的列车可以缩短至三节编组，能够大致反映车外流场。气动噪声计算模型采用简化的CRH 3。模型包括头车、中车、尾车，各长25 m，车高3.8 m，宽3.2 m，如图1所示。因本文目的是为了验证神经网络的适用性，省略了转向架、车厢连接、受电弓等对气动噪声有较大影响的部件。

图1 列车计算模型

列车气动噪声计算域为长方体形状，计算域宽80 m，高40 m，速度入口距离头车车鼻100 m，压力出口距离尾车车鼻175 m,列车离地面高0.325 m。地面设置为滑移壁面，列车车身设置为无滑移壁面，其余边界设置为对称边界。采用混合网格对流体区域进项网格划分，车身表面采用三角形网格。头车、尾车表面网格30 mm,中车网格50 mm。车身表面设置三层棱柱层网格，第一层距离车身表面2 mm。总网格约1 460万。

1.2 气动噪声计算模型

气动噪声计算根据Lighthill声类比理论，利用积分控制面法[15]进行计算。一般选取固体表面作为声源的积分面，将声源表面上的压力、密度、速度波动等信息作为声波方程的边界条件,并以此计算声音的远场辐射。本文采用的积分面法基于FW-H方程。

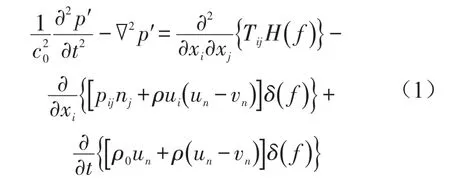
式中p′是待解声场参量，Tij为Lighthilll张量，ui为流体在xi方向上的速度分量，un为流体沿物体表面法向速度分量，vn为运动物体垂直于物体表面的法向速度分量，ρ0为无扰动时的流体密度，ρ为扰动后的流体密度，∇为哈密顿算子，f=0为隐函数描述的控制面方程，f＞0表示控制面外部区域，f＜0表示控制面内部区域，H（f）为Heaviside广义函数，其作用是将Lighthill应力张量引起的噪声限制在控制面以外区域，δ（f）为狄拉克三角函数。

2 神经网络模型

2.1 神经网络结构

神经网络种类繁多，BP神经网络是最广泛的一类。一个三层的BP神经网包括输入层、中间层、输出层。如图2所示[16]。

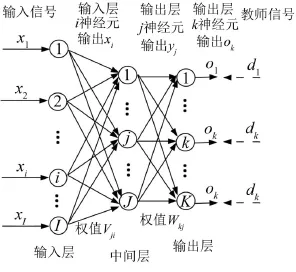
图2 神经网络结构

将输入信号（[x1；x2…xi…xI…]）输入网络，经过中间层传至输出层。教师信号为事先给定的训练目标，输出层与训练目标的误差达到可接受范围后，神经网络具有较好的预测能力。

假设输入层有i个节点，输出层有j个节点，中间层如有k个节点，Vji为输入层神经元到中间层神经元间的连接权；Wkj为中间层神经元到输出层神经元间的连接权。V为网络输入层神经元到中间层神经元间的连接权矩阵；W为网络中间层神经元到输出层神经元间的连接权矩阵。θ为中间层单元的阀值，φ输出层单元阀值。bi、cj分别为中间层节点的输出矢量和输出层节点的输出矢量。

中间层中的节点输出函数为[8]

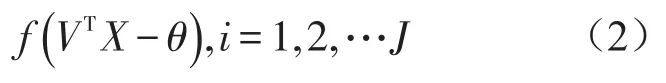
输出层中节点的输出函数为：

式中f( )为神经元激活函数。

输出层的神经元输出和教师信号的平方误差定义为

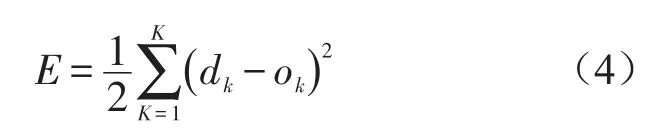
式中ok表示输出层神经元k的输出,dk为神经元k对应的训练目标。每一个输出都会与训练目标值产生一个误差，误差向前反馈，应用最小二乘平均原理，对中间层和输出层间的权值进行更新。

BP算法中的神经元输入输出函数应该是单调递增函数，隐层最常用的函数之一是双弯曲函数，（fx）=1/(1+exp(-x))。而在最后输出层用线性传递函数对输出进行值域扩展，常用函数为purelin。为提高收敛速度，使用对原有BP神经网络算法进行改进后的LM（Levenberg-Marquardt）算法[8]。

2.2 高速列车车外噪声预测模型

高速列车车外气动噪声跟很多因素有关，气动噪声的影响因素包括列车车型、列车行驶速度、路况、测点与列车的相对位置等。将车型设为影响参数X1，路况设为影响参数X2，行驶速度设为影响因素X3，测点相对于列车的横向位置视为影响因素X4，相对于列车的垂向位置视为影响因素X5，相对于列车的纵向位置视为影响因素X6，…。列车车外气动噪声总声压级SPL与各影响因素之间具有某种对应关系SPL=f(x1,x2,x3，x4，x5，x6…)，这种关系就是一个复杂的神经网络。利用现有的技术难以得出这种关系，但是一个三层的神经网络能够任意逼近函数。

高速列车车外气动噪声影响因素众多，为了简单明了验证神经网络的适用性，将测点与高速列车之间的相对位置作为气动噪声的影响因素，仅用神经网络预测列车过明线时，行驶速度为300 km/h速度下的车外气动噪声分布。假设车外某一噪声测点的气动噪声值跟该测点与列车的相对位置之间满足关系SPL=f(x,y,z)，此时的高速列车车外气动噪声预测模型具有三个输入变量，一个输出变量。中间层节点取10。预测模型如图3所示。

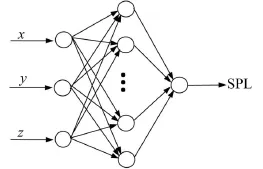
图3 车外气动噪声预测模型

2.3 网络训练与验证

进行预测以前，需要对建立的神经网络进行训练，使其建立某种应答机制。当输入参数变化时，神经网络会输出相应的值与其对应。训练样本选取应合理，样本包含的数据应能够反映整个系统总体变化规律，样本点应包含整个参数取值范围。在数值梯度变化大的地方，样本点应适当增加。训练样本由CFD仿真获得，将坐标系建立在头车车鼻处，XZ平面在水平地面上。坐标系与列车固合，如图4（a）、（b）所示。则车外空间点与列车的相对位置可以通过点的坐标直观体现。由于列车纵向对称，训练样本点位于列车一侧。文中通过神经网络预测0＜x＜25 m，0＜y＜10 m，-25 m＜z＜100 m所包含的空间区域的气动噪声。在车外距离地面高度为2 m、5 m、8 m的平面上选取神经网络模型的预测样本，每层样本点为75个。由于头车，尾车位置气动噪声数值较大，这两个位置的样本点更密。其中2 m高平面上的样本点布置方式如图4（a）、（b）所示。5 m、8 m高度平面上的样本布置方式相同。

训练完以后的神经网络模型是否具有精确的预测能力，还需要对其进行验证。部分训练样本及验证样本如表1。

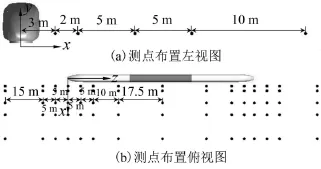
图4 训练样本点布置

神经网络训练时，对样本数据进行标准化处理，以消除数值本身引起的误差。网络训练时的误差变化曲线如图5所示，选用改进的LM算法，经过84个步长的训练，网络达到设定的精度要求（net.trainParam.goal=1×10-5）。验证样本点的预测结果与仿真结果的对比如图6所示，验证样本的仿真结果值如表1所示，将仿真结果作为参考值，绘制在图6中为一条斜率为1的直线。图6中散点为预测结果，散点的x坐标为仿真值，y坐标为预测值。预测结果与仿真结果的误差较小，均匀分布在直线两边。神经网络能够满足噪声的预测要求。

表1 部分训练样本及验证样本

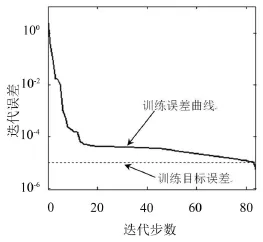
图5 网络训练误差变化曲线

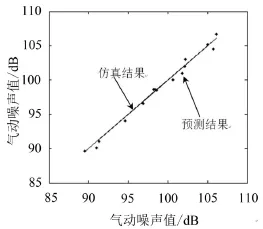
图6 验证样本预测结果与仿真结果对比

3 车外气动噪声预测

用经过训练的神经网络预测模型预测车外距离地面1.2 m高平面上的气动噪声，得到的气动噪声分布如图7所示。气动噪声在车头部位分布较大，其次是列车尾部。中车外的气动噪声值相对较小。

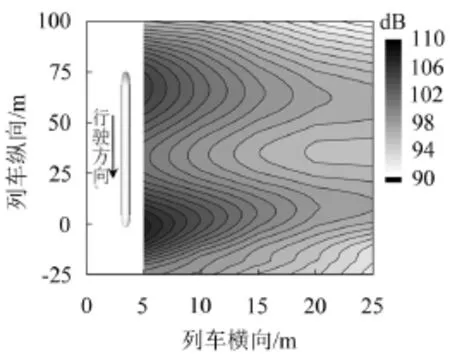
图7 车外距离地面1.2 m高平面气动噪声分布(dB)

4 结语

气动噪声计算资源需求大，耗时长。本文建立了基于数值优化方法的神经网络预测车外气动噪声的模型，并用高速列车气动噪声的计算值作为对比，预测结果与计算结果具有较小误差。神经网络预测结果表明，高速列车车外噪声在列车头部、尾部较大。中间车相对较小。预测方法相比现场实验与仿真计算，耗时大大减小。

本文不足之处在于文中的高速列车气动噪声模型相对简单，未考虑转向架、受电弓、车厢连接等重要位置，气动噪声计算值与真实值存在差异。预测结果仅针对文中模型。

[1]刘红光，陆森林.高速车辆气流噪声计算方法[J].交通运输学报，2002，2(2)：41-44.

[2]孙艳军，夏娟，梅元贵.高速列车气动噪声及减噪措施研究[J].铁道机车车辆，2009，29(3)：25-28.

[3]朱剑月，景建辉.高速列车气动噪声的研究与控制[J].国外铁道车辆，2011，48(5)：1-8.

[4]张军，黄艳艺，兆文忠.高速列车气动噪声数值仿真[J].大连交通大学学报，2012，33（4）：1-4.[5]刘加利.高速列车气动噪声特性分析及降噪研究[D].成都：西南交通大学，2013.

[6]刘加利，张继业，张卫华.高速列车表面气动噪声源研究[J].铁道车辆，2010，48（5）：1-5.

[7]郑征宇，李人宪.高速列车表面气动噪声偶极子声源分布数值分析[J].西南交通大学学报，2011，46(6)：996-1002.

[8]尹安东，张万兴，赵韩，等.基于神经网络的磷酸铁锂电池SOC预测研究[J].电子测量与仪器学报，2011，25（5）：433-437.

[9]张宝菊，雷晴，李刚，等.基于BP神经网络的人体血液中红细胞浓度无创检测[J].光谱学与光谱分析，2012，32（9）：2508-2511.

[10]段园培，李萍，薛克敏，等.TB8钛合金固溶组织研究及神经网络预测[J].稀有金属材料与工程，2012，41（8）：1426-1430.

[11]朱坚民，沈正强，李孝茹，等.基于神经网络反馈补偿控制的磁悬浮球位置控制[J].仪器仪表学报，2014，35（5）：976-984.

[12]江航，尚春阳，高瑞鹏.基于EMD和神经网络的轮轨故障噪声诊断识别方法研究[J].振动与冲击，2014，33（17）：34-38.

[13]田静宜，杨业，张思，等.高速列车齿轮箱故障诊断技术研究[J].制造业信息化,2013，6：77-78.

[14]马秀丽，刘芳，焦李成.基于免疫克隆算法的协同神经网络参数优化[J].红外与毫米波学报，2007，26（1）：38-42.

[15]耿冬寒，刘正先.大涡模拟-Light-hill等效声源法的空腔水动噪声预测[J].哈尔滨工程大学学报，2010，31（2）：182-187.

[16]朱凯，王正林.精通MATLAB神经网络[M].北京：电子工业出版社，2010.

ResearchonExteriorAerodynamicNoisePredictionofHigh-speed TrainsBasedonNeuralNetwork

LI Hui,XIAO Xin-biao,JIN Xue-song
(1.State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China; 2.Key Laboratory ofAdvanced Technologies of Materials,Ministry of Education, Southwest Jiaotong University,Chengdu 610031,China)

The neural network method was used to predict exterior aerodynamic noise of high-speed trains.Based on Lighthill’s acoustic analogy theory,an aerodynamic noise computation model of the high-speed train was built.Then,a neural network model for aerodynamic noise prediction was built up using Levenberg-Marquardt(LM)algorithm.The prediction model was trained by the sample data of the external aerodynamic noise signal,and the trained neural network model was used to predict the external aerodynamic noise.The results show that the neural network method for aerodynamic noise prediction is a quite accurate algorithm and can be used for exterior aerodynamic noise prediction of high-speed trains.

acoustics;high-speed trains;aerodynamic noise;acoustic analogy theory;neural network;prediction

U270.1+6

A

10.3969/j.issn.1006-1335.2015.03.013

1006-1355(2015)03-0056-04+116

2015－01－13

国家自然科学基金（U1434201）；国家863计划（2011AA11A103-4-2）

李辉（1989－），男，四川广安人，硕士研究生，目前从事铁路噪声方向研究。E-mail:lihui20091012@163.com

金学松，男，教授，博士生导师。E-mail:xsjin@home.swjtu.edu.cn