汽车内饰件用塑料挂钩CAE模型的DOE分析方法

王红，周厚林

(延锋百利得(上海)汽车安全系统有限公司，上海 201315)

汽车内饰件用塑料挂钩CAE模型的DOE分析方法

王红，周厚林

(延锋百利得(上海)汽车安全系统有限公司，上海 201315)

对汽车内饰用塑料挂钩在CAE设计中的方法进行了研究，采用DOE试验设计方法分析CAE模型中的产品设计要求(水平)与产品设计参数(因子)之间的关系，并通过响应曲线回归获得产品设计要求与设计参数之间的数学模型。所获得的数学模型可以替代CAE分析进行快速计算，使整个产品开发周期缩短。该方法值得在以后汽车产品CAE过程中应用。

塑料挂钩；安装力；脱出力；DOE试验设计方法；CAE分析

0 引言

当前，在汽车内饰件的安装过程中，大量使用塑料挂钩。在通过CAE(计算机辅助工程)对塑料挂钩设计参数与安装力和脱出力的关系进行研究过程中，针对所建立的简化CAE分析模型，定义的重要设计参数通常包括挂钩导入角、搭接宽度、支撑筋宽度3项设计参数(见图1)。同时，所定义安装力范围为26～55 N，脱出力范围为16～29 N。总体来说，所涉及的设计参数过多，且无法直观获得影响最大、最重要的设计参数。

基于此，在门内饰挂钩设计过程中，在CAE分析时，采用DOE(试验设计)的方法来进行试验设计。此时的CAE分析方法也类似于为一种试验方法，而DOE是对CAE分析进行试验设计。

1 建立CAE分析模型

为建立较精确的分析模型，文中采用挂钩角度为36°，支撑筋宽度为10 mm，搭接宽度 分别设为2、1.7和1.5 mm的样品进行试验，并用建立的CAE模型进行拟合和修正。实际样品测试结果见表1。

表1 塑料挂钩实际测量结果 N

基于表1的试验结果，经过多次拟合和优化后的CAE模型计算结果与实物测试结果差距较小，可进行假设检验。

2 DOE试验设计

在建立了CAE模型(见图2)之后，对3项主要设计参数与安装力及脱出力之间的关系进行DOE设计，采用2水平3因子分析矩阵，2水平分别为安装力和脱出力，3因子分别为搭接宽度、导入角和支撑筋宽度。同时进行2水平3因子加中性点并补充面接CCD，最终获得CAE计算数据见表2。

表2 3项主要设计参数与安装力及脱出力的DOE设计

对CAE计算的安装力和脱出力结果进行分析,结果显示:部分因子P>0.05,不显著。逐项删除非显著交互因子后，结果显示导入角对安装力和脱出力也都不显著，即导入角因子P>0.05,不显著且剩余的搭接宽度和支撑筋宽度两项因子与响应之间呈二次方关系。

如上结果显示，导入角的变化对安装力和脱出力的影响不大，故在塑料挂钩的设计中，可以采用较通用的导入角设计，不需要过多的关注和分析。

删除导入角因子，重新对支撑筋宽度和搭接宽度与安装力和脱出力进行响应曲面DOE设计。CAE计算数据见表3。

表3 2项主要设计参数与安装力及脱出力的响应曲面DOE设计

续表3

对CAE计算的安装力结果进行响应曲面分析，部分交互作用P>0.05,不显著。删除非显著交互作用，结果显示P<0.05，显著。可建立安装力分析模型，且模型可用。

如图3，采用Minitab计算软件对安装力与搭接宽度和支撑面宽度进行响应面回归计算，获得门盖挂钩安装力数学模型为：

式中：F1为门盖挂钩安装力；

W1为搭接宽度；

W2为支撑筋宽度。

对CAE计算的脱出力结果进行响应曲面分析，部分交互作用P>0.05,不显著。删除非显著交互作用，结果显示P<0.05，显著。可建立脱出力分析模型，且模型可用。

如图4，采用Minitab计算软件对脱出力与搭接宽度和支撑面宽度进行响应面回归计算，门盖挂钩脱出力数学模型为：

式中：F2为门盖挂钩脱出力；

W1为搭接宽度；

W2为支撑筋宽度。

如上，通过DOE方法，对塑料挂钩的3个关键设计参数与安装力和脱出力之间的关系进行了分析，首先如表2对3项主要设计参数与安装力及脱出力进行DOE设计，分析结果表明导入角对安装力和脱出力的影响较小。

其次如表3对两项主要设计参数与安装力及脱出力进行响应曲面DOE设计，并进行响应曲面回归计算，获得门盖挂钩安装力和脱出力数学模型。

如下对所获得的门盖挂钩安装力和脱出力数学模型及CAE分析方法的可靠性进行分析和验证。

3 结果分析

基于以上所建立的门盖挂钩安装力和脱出力数学模型进行可靠性分析和验证。

对如上所建立的挂钩安装力和脱出力数学模型作重叠等值线图，如图5所示。

考虑到搭接宽度由PAB门盖与仪表板本体两个零件确定，公差相对较大且易波动，所以把最佳参数区域选择在安装力和脱出力都对搭接宽度变化不太敏感的区域，即图5中灰色长方形区域。把长方形区域的中点作为最终选定的参数点开模制造样件，并进行实物测试，以验证DOE分析得出的数学模型。DOE模型推算结果与CAE分析结果对比见表4。

表4 DOE模型推算结果与CAE分析结果对比

对比DOE数学模型推算结果和CAE分析结果，两者差距较小，故安装力和脱出力数学模型可用。

最后，对选定的最优参数进行开模制造样件，并实际测量样件的安装力及脱出力，对比实际测量值与CAE分析值的差距，验证CAE分析方法及数学模型的准确性。对实际开模样品进行安装力和脱出力测量，所获得的试验结果见表5。

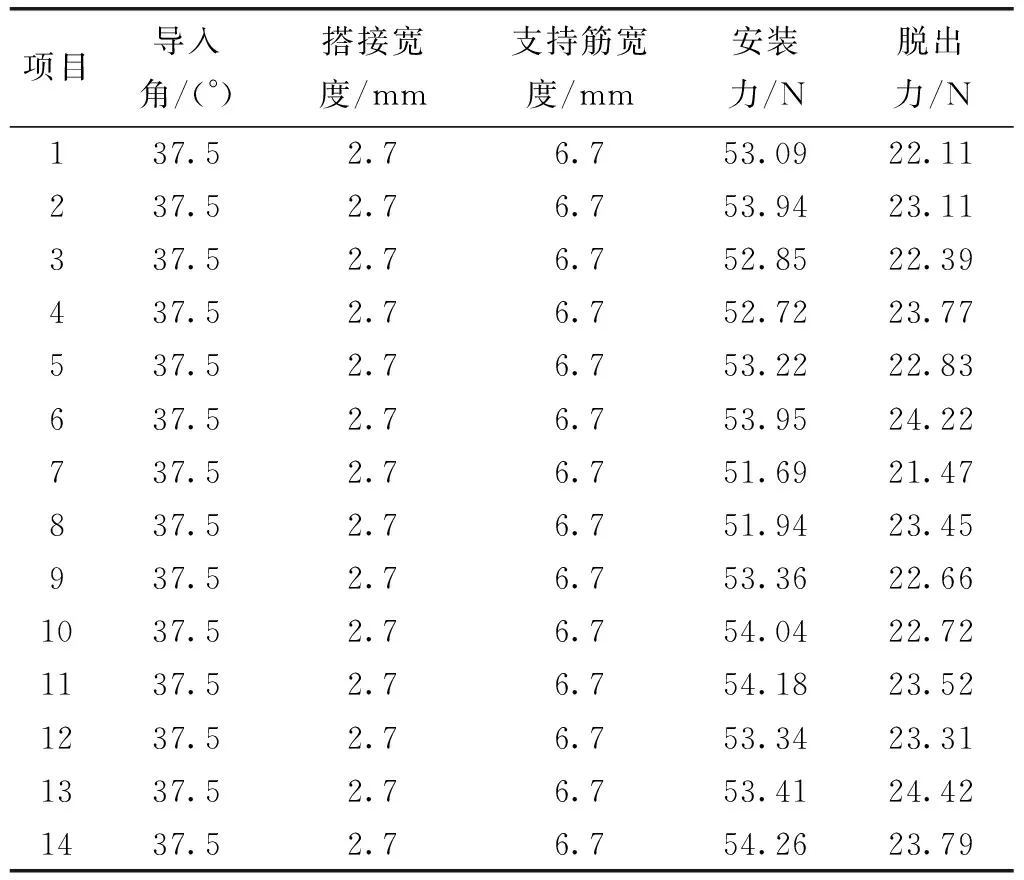
表5 实际样品测量结果

将表5中用实际样品测量的安装力和脱出力与CAE计算结果进行对照分析。如图6所示，安装力实测值与CAE计算值拟合程度高；如图7所示，脱出力实测值与CAE计算值拟合程度也高。

综上所述，按照文中选定的设计参数开模制造的样件，其试验结果与CAE计算结果之间的差别不大。文中根据DOE方法所获得的CAE分析模型能有效地预测设计参数变化对挂钩安装力和脱出力的影响趋势。

4 结论

文中研究成果包括：不仅指出了塑料挂钩设计时需关注的重要参数即搭接宽度和支撑筋宽度，建立了合适的CAE模型用于模拟和分析塑料挂钩搭接宽度及支持筋宽度与挂钩安装力及脱出力的关系。

更重要的是，文中提出了一种采用DOE方法进行CAE分析的思路，用试验设计的方法来分析产品设计要求(水平)与产品设计参数(因子)之间的关系。提高了CAE分析的精度，并可以通过响应曲线回归获得产品设计要求与设计参数之间的数学模型，所获得的数学模型可以替代CAE分析进行快速的计算，节省CAE分析的时间，缩短产品开发周期。

文中的研究不仅解决了汽车行业中内饰件塑料挂钩设计研究的难题，同时通过DOE的分析方法，也提高了CAE的分析精度，节省了开模成本和开发周期。

【1】 周厚林，王红.汽车内饰件用塑料挂钩安装力及脱出力研究[J].汽车零部件，2014(2):45-47.

DOE Analysis Method for Plastic Hook CAE Model

WANG Hong,ZHOU Houlin

(Yanfeng Key(Shanghai)Automotive Safety System Co., Ltd.,Shanghai 201315,China)

DOE analysis method was used to analyze the relation between the product requirements and design parameters in CAE model.The mathematics formulae were built to replace the CAE model by regression equation.This analysis method can reduce the CAE analysis time and component developing cost.

Plastic hook;Assembly force;Disassembly force;DOE experimental design method;CAE analysis

2014-12-03

王红(1981—)，学士，工程师，研究方向为汽车被动安全。E-mail：hwang1@yfkey.com。