基于炭黑环氧树脂基复合材料涂层的钢筋应变测量方法研究

毛清林，赵晓华

(汕头大学土木工程系，广东汕头515063)

近年来，智能材料在工程领域的应用受到越来越多人的关注［1－12］。将一定量的导电材料加入惰性材料中，不但可以增强其力学性能，而且可改善它的电性能［12］。进一步的研究发现，这一复合材料具有压电效应，电阻相对变化率与应变的变化呈现一定的规律性［1－5，8］。

钢筋为土木工程结构中的一种重要组成原料，其关系结构的安全。通过对钢筋力学状况的监测，可以感知整个结构的安全状况。目前还没有找到对结构中钢筋的力学状态进行长期监测的有效方法。本文通过监测纳米炭黑环氧树脂复合材料的状态来监测钢筋的力学状态。其基本原理是对钢筋表面用纳米炭黑、环氧树脂、界面处理剂复合材料处理，通过测量复合材料的电性能变化实现对钢筋的力学性状进行监测。

1 试验方法

1.1 材料及配比

钢筋为HPB235，直径14 mm。E－44环氧树脂和EP型环氧树脂固化剂由广州市东风化工实业有限公司生产。邻苯二甲酸二丁酯(C6H4(COOC4H2)2)由天津市科密欧化学试剂有限公司生产，浓度为99.5%。甲醛溶液(CH2O)的浓度为30.03%，由上海凌峰化学试剂有限公司生产。炭黑为超细黑色粉末，粒径33 nm，由山东淄博华光化工厂生产，其基本性能如表1所示。

炭黑环氧树脂基复合材料共采用3个配比(见表2)。按表2的配比分别称取各个组分，依次加入搅拌器中，边搅拌边加入炭黑，使炭黑分散均匀，得到均质的复合材料。

表1 炭黑的性能参数

表2 炭黑环氧树脂基复合材料的配比 g

1.2 试件制作

试件尺寸如图1所示。首先，在14 mm圆钢的中间测试部位用砂纸打磨，除去表面氧化层，用棉花蘸无水乙醇清洗表面，待乙醇挥发后，均匀涂上一层约0.2mm厚的环氧树脂(环氧树脂和固化剂的重量比为1∶1)作为绝缘层。此绝缘层固化、干燥后，在其上涂抹炭黑环氧树脂基复合材料，厚度约1 mm。其次，按图示阴影位置分别缠绕4根铜芯导线作为电极，继续涂抹炭黑环氧树脂基复合材料，直到完全包裹住铜芯导线(露出端部)，厚度约为2.5～3.5 mm。为使导线电极和复合材料有良好的电接触，最后在炭黑环氧树脂基复合材料涂层的表面紧紧缠绕纱布，然后将试件放置室内养护28 d。每组配比的试件数为6个。测试前在图示位置粘贴金属电阻应变片。

图1 试件尺寸

1.3 测试过程

对试件进行拉伸试验。采用3种加载方式:五级等幅循环加载、变幅加载和一次性破坏加载。等幅循环加载的最大荷载为136.45 MPa，变幅加载的每级最大荷载分别为 77.97 MPa、116.96 MPa、155.94 MPa 和 194.90 MPa，加载速率为 2.598 MPa/s。

加载过程中，同时测量炭黑环氧树脂基复合材料的电阻R和钢筋应变。电阻采用四电极法，由美国HP公司生产的Hewlett 34401A型数字化电表测量，并通过计算机自动采集。应变用IMP分散式数据采集系统自动测量和采集。

2 试验结果

试验中，相应于A、B和C三种配比的炭黑环氧树脂基复合材料表现出基本相同的行为。为简单起见，本文仅给出B组试件的测试结果。

图2为等幅循环加载时复合材料电阻相对变化率随钢筋应变的变化规律。由图2可以看出，对于每一个循环，钢筋应力和应变都保持线性关系，卸载后没有残余变形，表明钢筋在弹性范围内。炭黑环氧树脂基复合材料涂层的电阻相对变化率((R－R0)/R0)与应变有很好的单调对应关系，大致呈线性变化，其随应变的增加而增加，随应变的减少而减少。单位应变的电阻相对变化率大约为1.4。

图3为变幅循环加载时复合材料电阻相对变化率随钢筋应变的变化规律。由于荷载的最大幅值为194.90 MPa，因而在每一循环内，钢筋都在弹性范围。由图3可以看出，复合材料涂层的电阻相对变化率随应变呈现出规律性的变化，其随应变的增加单调增加，随应变的减少单调减少。

图2 等幅循环加载时复合材料电阻相对变化率随钢筋应变的变化规律(R0=289.18 Ω)

图3 变幅循环加载时复合材料电阻相对变化率随钢筋应变的变化规律(R0=299.12 Ω)

图4为一次性加载至钢筋断裂时复合材料电阻相对变化率随钢筋应变的变化规律。与图2和图3相似，钢筋在弹性范围内时，复合材料涂层的电阻相对变化率随应变大致呈线性变化，其随应变的增加单调增加，但钢筋屈服后，应变急剧增加。与此同时，电阻相对变化率也急剧上升，其变化幅度要大大高于应变的变化。尽管电阻相对变化率与应变不再线性变化，但两者仍然保持很好的对应关系。

综上所述，复合材料涂层的电阻相对变化率不仅能够反映钢筋弹性范围内的变形，而且在钢筋屈服后能够反映钢筋的损伤与断裂。

图4 一次性加载时复合材料电阻相对变化率随钢筋应变的变化规律(R0=380.15 Ω)

3 应变测量原理

试件中炭黑环氧树脂基复合材料涂层的电阻计算公式为

式中:ρ为复合材料涂层的体积电阻率;l为测试段的长度;A为涂层横截面的面积。电阻相对变化率(RR0)/R0为

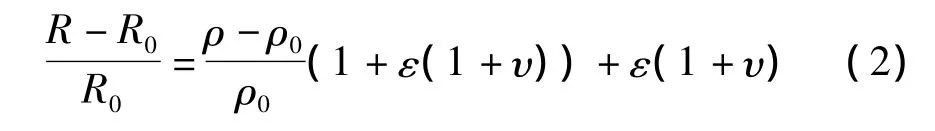
式中:R0为初始电阻;ε为拉伸应变;ν为泊松比。

式(2)表明，电阻相对变化率由两种原因产生，第一项为复合材料涂层的体积电阻率相对变化，第二项反映复合材料涂层在拉伸变形后其几何尺寸的改变。

研究表明，炭黑环氧树脂基复合材料的导电行为由炭黑颗粒间的隧道效应所产生，隧穿电流的计算公式［9］为

式中:j0、α、e0为材料常数;w为炭黑颗粒间的间隙宽度;e为间隙电压。加载过程中，测量电压保持不变，间隙电压为常数。式(3)表明，隧穿电流仅取决于炭黑颗粒间的间隙宽度w，是间隙宽度w的负指数函数。由此可以推断，在恒温时，电导率σ0为

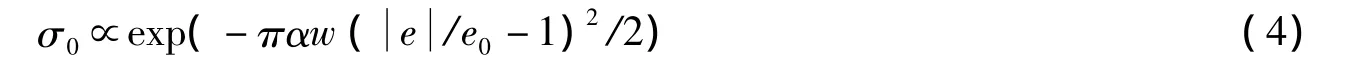
由于体积电阻率为电导率的倒数，因此有

则

代入式(2)，得

式(7)即为炭黑环氧树脂基复合材料涂层的电阻相对变化率随应变变化的规律。由式(7)可以看出，电阻相对变化率是应变的指数函数。

由于εw通常很小，利用泰勒展开，有

则式(7)可近似为

式(9)表明，电阻相对变化率与应变有非线性关系。当应变很小时，可忽略ε的高阶项，式(9)简化为

此时，电阻相对变化率随应变线性变化，可进一步表示为

式中K为灵敏系数，仅与复合材料涂层的材料常数和间隙电压有关。间隙电压一定时，K为常数。在钢筋弹性范围内，相应本文条件的K值大约为1.4。当复合材料的泊松比为0.3时，式(10)的第一项值很小，说明复合材料体积电阻率的相对变化值很小。但钢筋屈服后，随着应变的急剧增加，K值迅速增大，比弹性范围要高出一个数量级，此时复合材料的体积电阻率相对变化值占据主导地位。

以上分析与试验结果相一致。因此，只要测量复合材料涂层的电阻变化，就可以达到测量钢筋应变的目的。钢筋在弹性范围内时，应变很小，复合材料涂层的电阻相对变化率(R－R0)/R0与应变可按线性关系考虑。钢筋屈服后，复合材料涂层的电阻相对变化率应考虑应变的非线性行为。

4 结论

本文提出了用炭黑环氧树脂基复合材料涂层测量钢筋应变的思想。拉伸试验显示，复合材料涂层的电阻相对变化率与钢筋应变有很好的单调对应关系。在钢筋弹性范围内，复合材料涂层的电阻相对变化率与钢筋应变大致呈线性关系，其随应变的增加而增加，随应变的减少而减少。钢筋屈服后，复合材料涂层的电阻相对变化率随钢筋应变的增加而急剧增大。

在此基础上，基于隧道效应理论，导出了电阻相对变化率与应变的数学解析式。钢筋在弹性范围内时，应变很小，复合材料涂层的电阻相对变化率与应变近似为线性关系。钢筋屈服后，复合材料涂层的电阻相对变化率应考虑应变的非线性行为。用炭黑环氧树脂基复合材料涂层可有效测量钢筋的应变，测量过程简单。

［1］ Wang X，Chung D D L.Self－monitoring of fatigue damage and dynamic strain in carbon fiber polymer－matrix composites［J］.Composites Part B ，1998(29B):63－73.

［2］ Schueler R，Joshi S P，Schulte K.Damage detection in CFRP by electrical conductivity mapping［J］.Composites Science and Technology，2001，61:921 －930.

［3］ Wen S，Chung D D L.Pitch －matrix composites for electrical，electromagnetic and strain －sensing applications［J］.Journal of Materials Science，2005，40:3897 －3903.

［4］ Wang S，Chung D D L.Negative piezoresistivity in continuous carbon fiber epoxy－matrix composite［J］.Journal of Materials Science，2007，42:4987 －4995.

［5］ Hussain M，Choa YH，Niihara K.Conductive rubber materials for pressure sensors［J］.Journal of Materials Science Letters，2001，20:525 －7.

［6］ He X，Chen F，Chen X.PTC effect of carbon black filled polypropylene［J］.Journal of Materials Science Letters，2001，20:589－590.

［7］ Qian D，Wager G J，Liu K W，et al.Mechanics of carbon nanotubes［J］.Applied Mechanics Reviews，2002，55:495－532.

［8］ Kang L，Schulz M J，Kim J H，et al.A carbon nanotube strain sensor for structural health monitoring［J］.Smart Materials and Structures，2006，15:737 －748.

［9］ Chung D D L.Comment on Piezoresistive Effect in SiOC Ceramics for Integrated Pressure Sensors［J］.J Am Ceramic Soc，2011，94(1)，:289.

［10］ Chung D D L.Carbon Materials for Structural Self－ Sensing，Electromagnetic Shielding and Thermal Interfacing［J］.Carbon，2012，50:3342 －3353.

［11］ Shuang Lu，Chung D D L.Viscoelastic behavior of silica particle compacts under dynamic compression，ASCE Journal of Materials in Civil Engineering，2014，26(3)，551 －553.

［12］ 汤浩，陈欣方，罗云霞.复合型导电高分子材料导电机理研究及电阻率计算［J］.高分子材料科学与工程，1996，12(2):1－7.