基于离散元的节理岩体水工隧洞地震动力特性分析

包 磊，陈春武，潘 昆，罗晓琴，张 金，雷进生

(1.国家林业局 昆明勘察设计院，昆明 650216;2.三峡大学土木与建筑学院，湖北宜昌 443002)

1 研究背景

天然岩体通常可看作是由完整岩石和不连续面如层面、节理断层等组成，不连续面的存在使得岩体的完整性和均匀性受到不同程度的破坏，岩体中的这些不连续面对岩体在静力和动力荷载作用下的力学行为均起到主导作用［1］。显然，基于连续介质理论的有限元方法难以克服因建立的分析模型与岩体介质客观属性之间存在的差异对模拟结果产生的不利影响。目前关于隧洞围岩稳定性的研究主要集中于静力分析，对一般隧洞在动荷载作用下的研究也取得了一系列成果，但对于大跨度、高边墙的节理岩体隧洞在动力作用下的围岩力学响应研究较少;加之已有的研究大都基于小变形的假设，事实上，在高应力或动荷载的作用下，节理岩体要产生剪切滑移、离层脱落甚至失稳垮塌，这些现象已非连续介质所能描述。因此，本文主要讨论地震作用下大跨度、高边墙且含节理裂隙等软弱结构面条件下的水工隧洞围岩的力学响应，获得大型地下隧洞不同部位围岩在地震中的响应规律，以期为同类大型地下工程的设计和施工及进一步分析地震作用下围岩的变形破坏过程提供参考。

2 动力离散元求解原理

UDEC是一个处理不连续介质的二维离散元程序，可用于模拟非连续介质承受静载或动载作用下的响应。非连续介质被认为是由离散的块体集合体表示，块体间的边界接触面以不连续面处理，允许各个离散块体沿不连续面发生较大的位移和转动，而这恰好体现了节理岩体的重要变形和破坏机制。在离散单元法中，不连续面等结构面在赋予相关节理参数后，主要采用Jset命令生成节理组。

在离散元法中，块体的运动方程都可归结为如下形式［2－3］，即

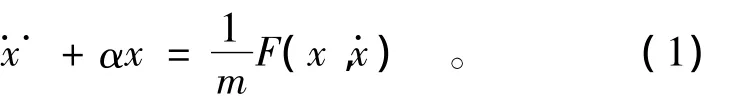
设an，vn和Fn分别为tn时刻的加速度、速度和力，开始时刻 t0=0，时步为Δt，则tn=t0+nΔt，可将式(1)改写为

用显式的Newmark法对上式积分，其过程如下:

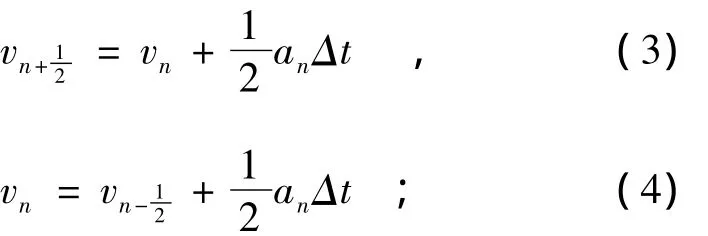
则在时刻tn的加速度可由式(3)和式(4)求出，即

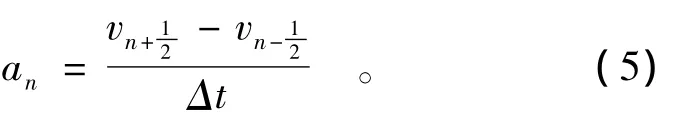
类似地可求得tn时刻的速度为

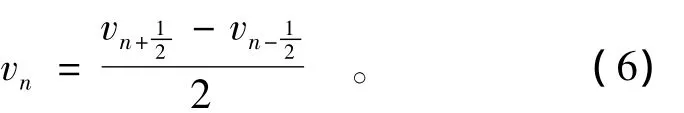
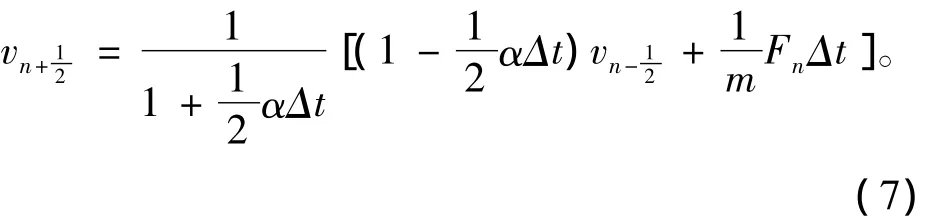
则易求块体在tn+1时刻的位置，即

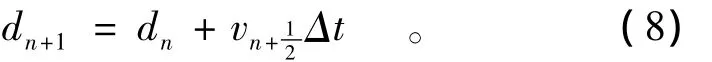
如此往复，利用上述数值法求解非线性微分方程(1)，中间时刻t(2n+1)/2时的速度是一个重要的中间变量，通过它就很容易求得块体的新位置和当前时刻的加速度。

根据上述的显式积分方法，依次进行3个主要的循环计算，即所有块体→所有接触→所有块体间空洞。在输入的动载荷引入之前，要一直重复上述的循环计算。

在上述的数值方法中，要保证计算的收敛和稳定，对于计算时步在小于一个限值的情况下才能满足要求，其物理含义为:在非常短的时间内，系统中某一点的扰动只对与该点相邻的单元有影响，而对系统中远离该扰动点的其它点不会产生影响［4－5］。对于这样的非线性问题的求解，Cundall给出了时步的相限值估算公式［5］，即

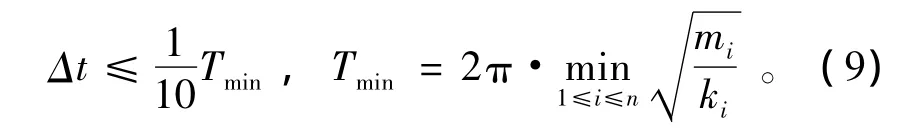
式中:Tmin为任一单元的最小固有振动周期;mi，ki分别为块体质量和刚度;n为块体数。

3 离散元动力计算模型的建立

以某大型水电工程尾水隧洞为工程背景，尾水主洞标准开挖断面为22 m×36 m(宽×高)的城门洞型，为典型的大跨度、高边墙工程，且地质条件复杂。尾水隧洞位于，，缓倾角层状岩体中，以厚至巨厚层砂岩为主，局部呈薄至中厚层状，绝大部分为微风化—新鲜岩体，以砂岩为主，围岩类型以Ⅱ—Ⅲ类为主，岩石坚硬，强度较高。厂房区无较大断层通过，岩体中发育的结构面主要有层面、层间软弱夹层和节理裂隙，节理裂隙主要有2组，优势产状分别为:275°～286°/NE∠55°～65°(J1)，70°～80°/NW∠62°～74°(J2)，节理裂隙发育段为Ⅲ类。地下厂房厂区实测地应力的最大主应力平均值为10 MPa左右，属中等低应力场，因此，岩体的动力响应仍以地质结构面控制型为主。

3.1 模型范围

模型边界必须足够远，以致模型对边界不产生影响。一般对单一地下开挖工程，边界离开挖边界的距离应不小于开挖跨度的5倍［6］。为降低过小的计算尺寸对模拟分析结果的影响，模型x方向计算宽度取为300 m，y方向计算高度取250 m，其中洞室底板距模型下边界为100 m。因地下隧洞埋深较浅，构造应力不明显，按不利情况考虑，假设初始地应力场仅涉及自重应力场。对隧洞上方300 m以上至地表的岩体则计算出其重量作为外荷载施加于上边界上。建立UDEC模型如图1所示。

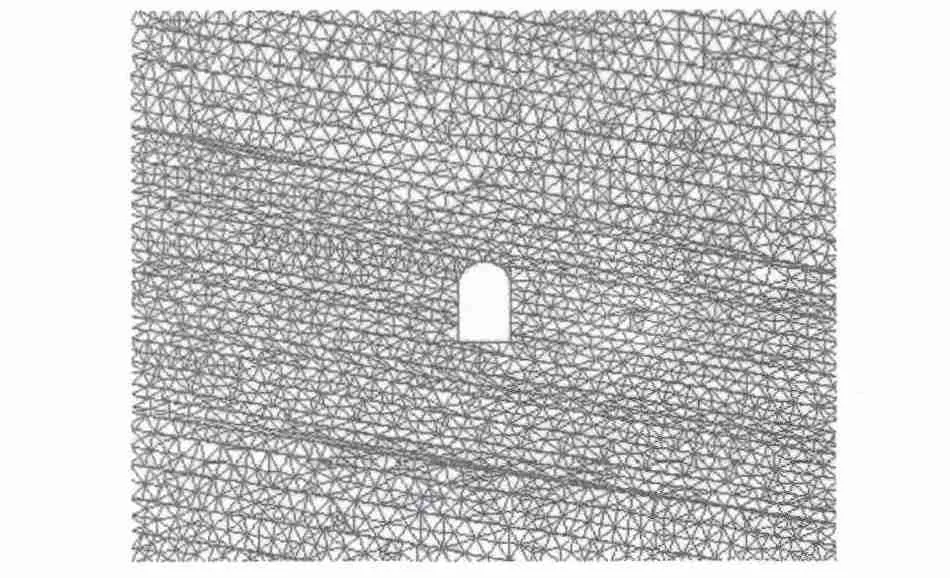
图1 开挖后的计算模型Fig.1 Calculation model of tunnel after excavation

3.2 地震荷载输入

考虑到剪切波对洞室响应影响较大，本节采用速度形式的垂直向剪切正弦波作为动力荷载输入至模型底部，速度时程表征为v=λsin(2πft)，取速度峰值 vs=0.1 m/s，频率 f=50 Hz，持时 t=0.1 s，计算0.2 s。波形如图2所示。

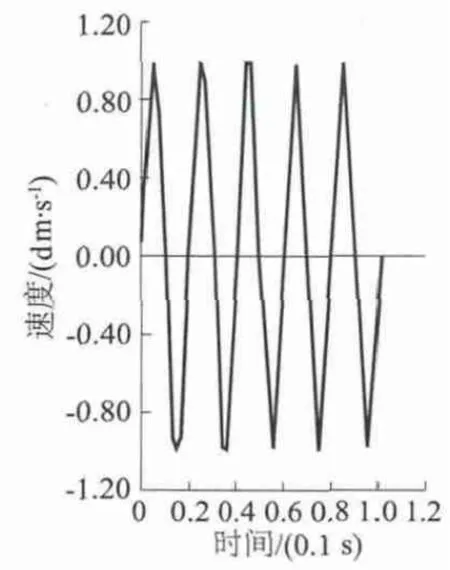
图2 正弦剪切波速度时程曲线Fig.2 Time-history curve of the velocity of sine shear wave

3.3 边界条件和阻尼

边界条件采用UDEC自带的自由场黏性边界，左右两侧的边界通过自由场网格与模型之间的黏性阻尼筒耦合来实现，以吸收来自模型内部的入射波，底部采用自由场边界并限制 x向和 y向位移［7－8］。本节动力荷载是速度历程形式的正弦剪切波，因无法直接将这种形式的动力荷载施加在不反射边界上，此时，可以按式(10)和式(11)将速度历程形式的动力荷载转换为式(12)应力历程形式的动力荷载［4］，转换后相当于在模型底部施加了一个幅值约为1 MPa的剪切应力波。

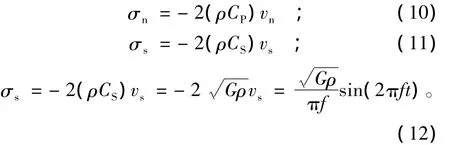
式中:σn为施加的法向应力荷载(MPa);σs为施加的切向应力荷载(MPa);ρ为介质的密度(kg/m3);CP为应力波在介质中传播的P波(纵波)波速(m/s);CS为应力波在介质中传播的S波(横波)波速(m/s);vn为铅直方向的质点速度(m/s);vs为水平方向的质点速度(m/s)。

对于岩土动力非线性问题，阻尼参数的确定通常采用Rayleigh阻尼，围岩的阻尼比一般为0.01～0.03［9］，本文阻尼比取0.01进行计算。

3.4 本构关系

数值计算中，对于岩石，采用理想弹塑性模型，以Mohr－Coulomb强度准则作为其屈服准则，屈服函数如下:

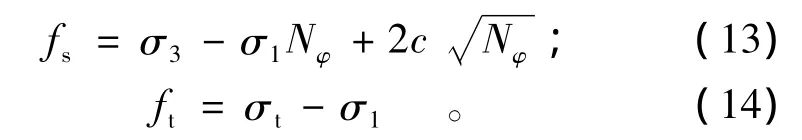
式中:σ1，σ3分别为最大、最小主应力;φ为内摩擦角;c为黏聚力;σt为岩石的抗拉强度。Nφ的表达式为

当岩体内某点应力满足fs＞0时，发生剪切破坏;当满足ft＞0时，产生拉伸破坏。

对于岩体节理，适用弹性模型，屈服准则为接触Coulomb 滑动准则［10］，即

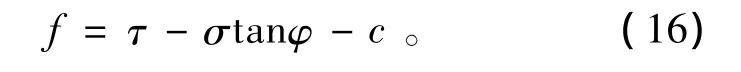
式中σ，τ分别为节理面正应力和剪应力。

3.5 岩体物理力学指标

一般而言，岩石节理和材料的动态物理力学特性参数都是与应变速率相关的，但对于岩体的变形模量E和泊松比ν等参数随应变率的变化幅度很小，通常用相应的静态参数表示［11－12］，故动力分析岩体物理力学参数取值同静力分析。结合工程勘察资料分别给出水工隧洞各岩层及结构面的岩体力学参数，见表1和表2。

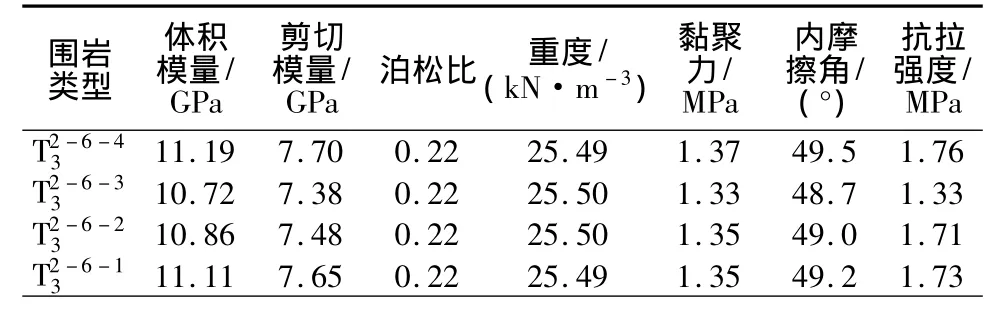
表1 尾水洞洞室围岩的物理力学参数Table 1 Physical and mechanical parameters of surrounding rock of the tailrace tunnel

表2 尾水洞洞室结构面物理力学参数Table 2 Physical and mechanical parameters of structural planes of the tailrace tunnel

4 计算结果与分析

计算过程包括静力和动力计算2部分，动力分析以静力计算为前提，计算步骤如下:

(1)首先静力计算。施加自重和构造荷载作用使模型固结，以模拟初始地应力场的形成。

(2)其次开挖、支护。分层分步开挖、支护应使模型达到平衡状态，直至整个洞室开挖支护完成为止。

(3)最后动力分析。施加地震作用力，研究大跨度、高边墙且含节理裂隙等软弱结构面条件下的水工隧洞围岩的动力响应。为分析洞室的开挖对地震波在介质中传播速度的影响，在模型中部水平方向和垂直方向各选取10个点进行监测。各监测点布置如图3所示。

4.1 动荷载对隧洞围岩动力响应分析

地下洞室围岩中各监测点的速度时程曲线可反映出介质对动力荷载的实时响应。通过对顶拱、边墙及底板监测点的速度监测发现，剪切波在0.01 s后传至底板部位，在0.02 s后传至拱顶部位，在0.015 s后传至左右边墙部位;在垂直方向，顶拱速度幅值约为0.043 m/s，小于底板速度幅值为0.086 m/s;水平方向，左边墙速度幅值约为0.026 5 m/s，右边墙速度幅值约为0.025 0 m/s。洞壁监测点在考虑垂直方向正弦剪切地震波的作用下，各监测点速度历程反映了输入地震波的振动特性，且竖向动力特性明显比水平方向大。

图4(a)为水平方向10个监测点H10—H19的速度历程曲线，图4(b)为竖直方向10个监测点V20—V29的速度历程曲线。

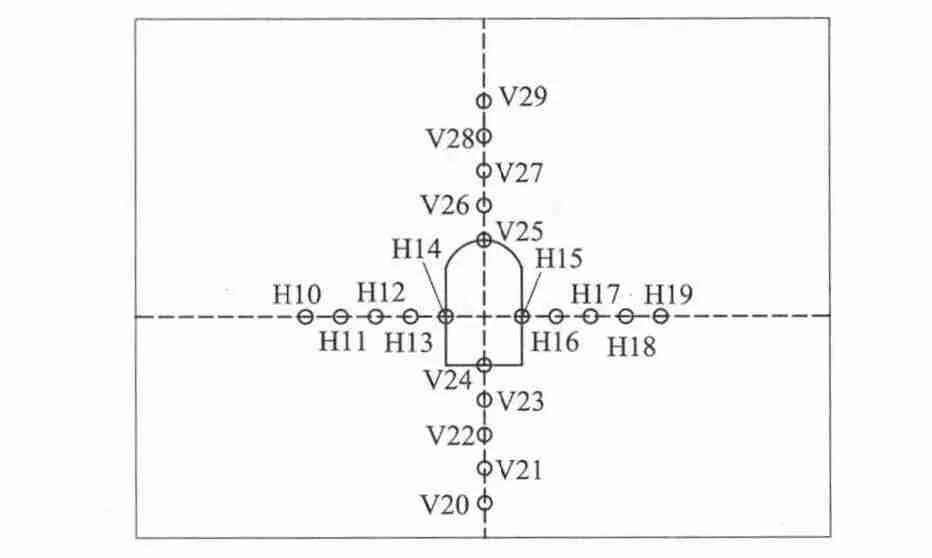
图3 监测点布置Fig.3 Arrangement of monitoring points

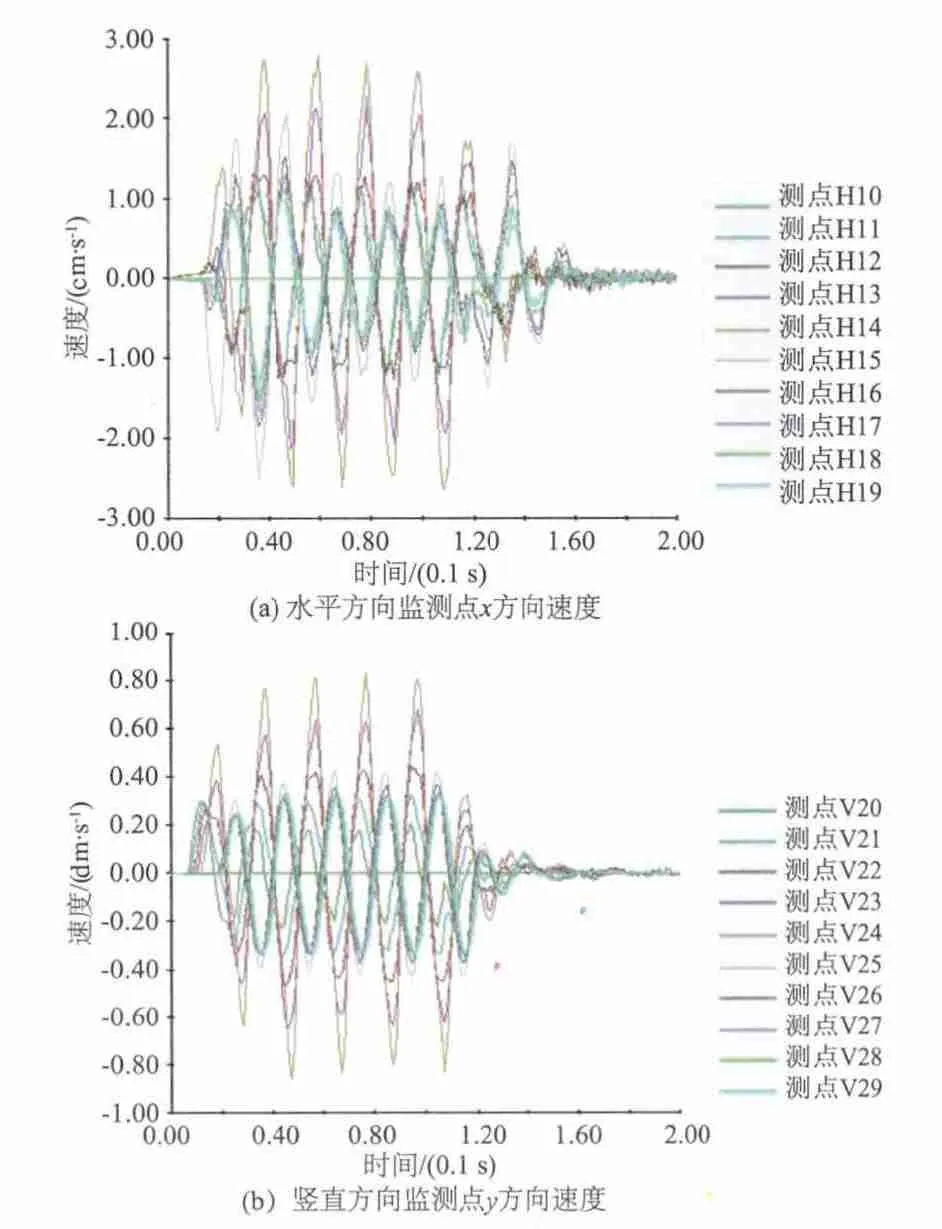
图4 不同位置监测点x和y方向的速度时程曲线Fig.4 Time-history curves of wave velocity in direction x and y of monitoring points

结合图3及图4可以看出，地下洞室洞周附近点速度幅值明显大于远离开挖轮廓面附近介质监测点的速度幅值，反映了地下洞室开挖断面的存在对剪切波具有放大效应。由此可见，形成开挖面的地下洞室在动荷载作用下的稳定性程度降低。整体而言，地下洞室洞监测点速度幅值变化反映了波在介质中传播的衰减规律特性，即离波源越远的监测点由于所受波扰动小，因而速度幅值也较小。

4.2 动荷载对隧洞围岩位移影响

地震荷载作用下，大跨度、高边墙节理岩体中，洞室开挖断面对围岩位移分布的影响可通过对开挖轮廓线附近的监测点的位移历程曲线来反映。图5为水平方向监测点x方向位移历程曲线(洞室左边墙监测点:H10—H14;右边墙监测点:H15—H19)，图6为竖直方向监测点y方向位移历程曲线(洞室底板部位监测点:V20—H24;顶拱部位监测点:V25—V29)。

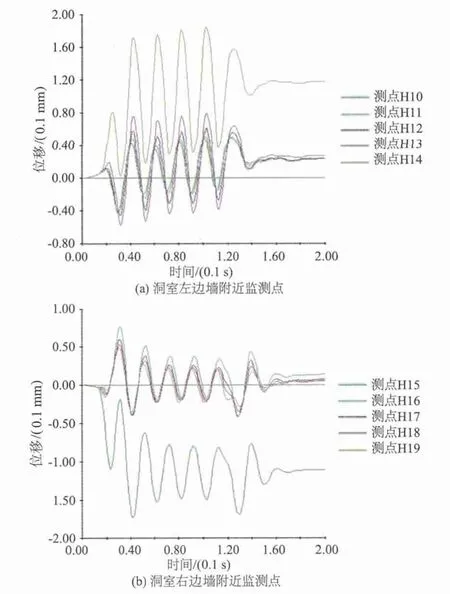
图5 水平方向监测点x方向位移时程曲线Fig.5 Time－history curves of displacement in direction x of monitoring points at horizontal direction

由图5和图6可以看出，在靠近开挖断面，位移值明显大于远离开挖面部位，顶拱、底板及边墙部位均表现出相似的规律。分析认为，洞室的开挖，使原处于一定地质环境中的岩体应力释放，岩体卸荷回弹，越靠近开挖面，卸荷量越大，围岩变形也越明显。

地震波作用后，隧洞围岩位移场分布如图7所示。震后围岩最大位移为0.297 mm，围岩在经过最优开挖支护方案的实施以后，整体效果明显，位移值增量不大，位移矢量方向多指向开挖临空面。由于地震的频率较集中于低频，对长周期结构物或构筑物有较大的影响，而岩体的自振频率较小，在介质自振频率和地震波频率接近的情况下达到共振，此时洞室的响应破坏也最为明显，本节输入地震波频率超过介质共振频率，故其对围岩位移场影响较小。

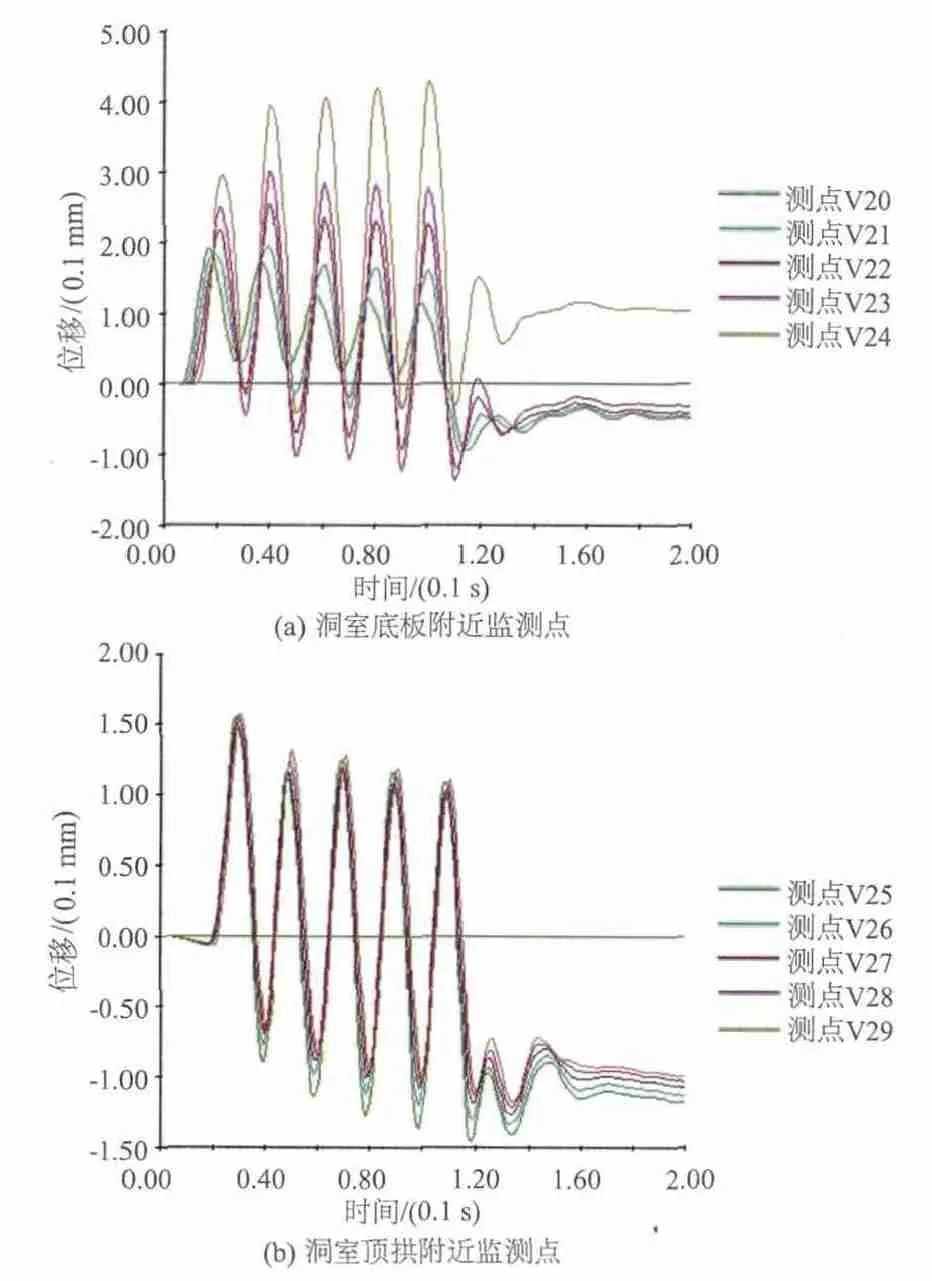
图6 竖直方向监测点y方向位移时程曲线Fig.6 Time－history curves of displacement in direction y of monitoring points at vertical direction

图7 震后围岩位移矢量图Fig.7 Displacement vectors of surrounding rock after earthquake

4.3 动荷载对隧洞围岩应力影响

表3给出了各监测震前、震后点水平应力σxx和竖向应力σyy的应力幅值(负号表示受压)。

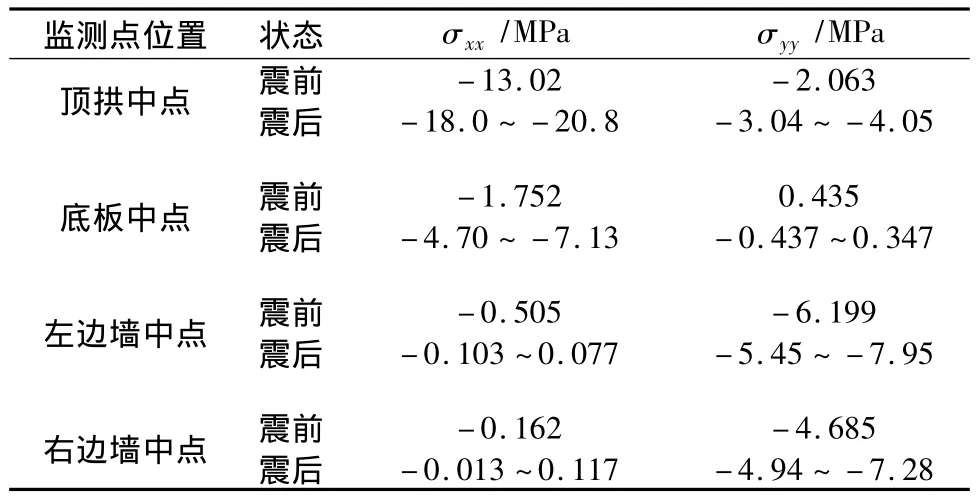
表3 各监测点震前、震后水平应力和竖向应力幅值Table 3 Horizontal stress and vertical stress amplitudes of monitoring points before and after earthquake

由表3可以看出，竖向正弦剪切地震波作用后，洞室各监测点应力值相对地震波作用前均有不同程度的增大，由于施加的动力荷载幅值量级不大，约为1 MPa，所以受动载影响应力增大幅度不大。不难发现，相对震前竖向地震波的作用对顶拱和底板的水平应力值的影响程度明显大于其对竖向应力的影响;而在边墙部位，地震波作用后，监测点水平应力却有一定程度减小，其对监测点竖向应力值影响不大。因此，在隧洞受竖向地震作用下，顶拱和底板部位应加强支护和监测，以确保洞室的安全。

洞室底板和左右边墙中点监测点在地震波作用下，先后分别表现出压应力和拉应力，然而出现拉应力时的量值小于出现压应力时的量值，局部微小拉应力的出现因范围和量值均很小，不足以使围岩和节理破坏，对围岩整体稳定影响不大。

应力场计算显示，地震作用前后围岩拉应力及压应力均有一定程度增加，但幅度不大，洞室处于稳定状态。

4.4 动荷载对隧洞围岩塑性区影响

地震波作用前后，隧洞围岩塑性区分布如图8所示。与震前相比，震后的围岩塑性区有较大幅度增加，数量由震前的28增至115，增幅为4倍，对比发现，震后隧洞边墙及底板岩体塑性区范围扩大较明显，地震作用前后拉伸破坏数量均为0。

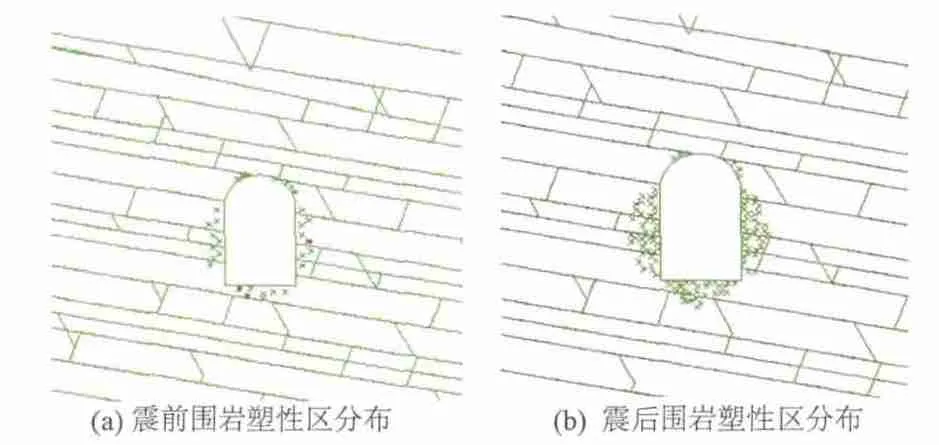
图8 地震波作用前后围岩塑性区分布Fig.8 Distribution of plastic zones of surrounding rock before and after earthquake

5 结论

(1)地震波在节理岩体中传播符合波的衰减规律;在垂直方向正弦剪切地震波的作用下，各监测点竖向动力特性明显比水平方向大;同时，地下洞室洞周附近点速度幅值明显大于远离开挖面附近介质监测点的速度幅值，即地下洞室开挖断面的存在对剪切波具有放大效应。

(2)在地震波作用过程中，围岩介质质点位移幅值逐渐增大，地震波作用完毕，在岩体介质阻尼的作用下，各监测点位移幅值发生了很小的永久变形后趋于稳定。在垂直方向正弦剪切地震波的初期，边墙产生的位移值大于顶拱，随时间的推移，边墙受地震力作用变小，从而产生的位移变化量小，而底板围岩变形受地震作用较大，即底板的变形更为敏感;由洞室断面附近的水平和竖直方向监测点位移历程可以看出，洞室的开挖，使原处于一定地质环境中的岩体应力释放，岩体卸荷回弹，在靠近开挖断面，位移值明显大于远离开挖面部位，顶拱、底板及边墙部位均表现出相似的规律;而围岩整体位移由于介质自振频率小于输入地震波频率，故地震波对围岩位移场影响较小。

(3)竖向正弦剪切地震波作用后，洞室各监测点应力值相对地震波作用前均有较小程度的增大。相对震前情况，竖向地震波对顶拱和底板的水平应力值的影响程度明显大于其对竖向应力的影响;而在边墙部位，地震波作用后，监测点水平应力却有一定程度减小，其对监测点竖向应力值影响不大，顶拱和底板部位应加强支护和监测;地震作用前后围岩最大拉应力及最大压应力均有一定程度增加，但幅度不大。

(4)与震前相比，震后的围岩塑性区有较大幅度增加，震后隧洞边墙及底板岩体是塑性区范围扩大较明显的部位。

6 讨论

UDEC是一个处理不连续介质的二维离散元程序，可用于模拟非连续介质承受静载或动载作用下的响应，非连续介质被认为是由离散的块体集合体表示，块体间的边界接触面以不连续面处理，允许各个离散块体沿不连续面发生较大的位移和转动，而这些恰好体现了节理岩体的重要变形和破坏机制。

本文研究获得大型地下隧洞不同部位围岩在地震中的响应规律，为进一步分析地震作用下围岩的变形破坏提供参考，可为类似大型地下洞室的工程设计和施工提供借鉴和参考。建议下一步研究工作如将离散单元法计算结果与其他较成熟有限元方法所得结论对比论证，使计算结果更符合客观实际。

［1］GOODMAN R E.Methods of Geological Engineering in Discontinuous Rocks［J］.West Publishing，1976，8(2):135－140.

［2］套炼金，常 春.节理岩体的动力响应分析及工程应用［J］.黑龙江矿业学院学报，2000，10(4):6－10.(TAO Lian-jin，CHANG Chun.Dynamic Response A-nalysis of Jointed Rock Mass and Its Application in Engineering［J］.Journal of Heilongjiang Mining Institute，2000，10(4):6－10.(in Chinese))

［3］陶连金，张悼元，王泳嘉.复杂工程岩休稳定性评价的方法与实践［M］.成都:成都科技大学出版社，1998.(TAO Long-jin，ZHANG Dao-yuan，WANG Yong-jia.Stability Evaluation for Complex Engineering Rockmass:Methods and Practice［M］.Chengdu:Chengdu University of Science and Technology Press，1988.(in Chinese))

［4］Itasca Consulting Group.UDEC(Universal Distinct Element Code)User’s Manual(Version 3.0)［M］.USA:Itasca Consulting Group，Inc.，1996.

［5］王泳嘉，邢纪波.离散元法及其在岩土力学中的应用［M］.沈阳:东北工学院出版社，1991.(WANG Yong-jia，XINGJi-bo.The Discrete Element Method and Its Application in Rock and Soil Mechanics［M］.Shenyang:Northeast Institute of Technology Press，1991.(in Chinese))

［6］王 涛，熊 将，郭武祥，等.地震荷载作用下地下厂房围岩稳定的离散元计算方法研究［J］.长江科学院院报，2009，26(12):58－61.(WANG Tao，XIONG Jiang，GUO Wu-xiang，et al.Research on Stability of Rock Mass around Underground Powerhouse Cavern by Discrete Element Method under Earthquake［J］.Journal of Yangtze River Scientific Research Institute，2009，26(12):58－61.(in Chinese))

［7］王鲁明，赵 坚，华安增，等.节理岩体中应力波传播规律研究的进展［J］.岩土力学，2003，24(增):602－610.(WANG Lu-ming，ZHAO Jian，HUA An-zeng，et al.The Progress in Study of Regularity of a Stress Wave Propagation in the Jointed Rock Mass［J］.Rock and Soil Mechanics，2003，24(Sup.):602－ 610.(in Chinese))

［8］陶连金，张悼元，傅小敏.在地震载荷作用下的节理岩体地下洞室围岩稳定性分析［J］.中国地质灾害与防治学报，1998，9(2):33－42.(TAO Lian-jin，ZHANG Zhuo-yuan，FU Xiao-min.Stability Analysis of Surround-ing Rockmass of Underground Excavation Rock Mass Under Seismic Load［J］.The Chinese Journal of Geological Hazard and Control，1988，9(2):33－ 42.(in Chinese))

［9］郑颖人，肖 强，叶海林，等.地震隧洞稳定性分析探讨［J］.岩石力学与工程学报，2010，29(6):1081－1088.(ZHENG Ying-ren，XIAO Qiang，YE Hai-lin，et al.Study of Tunnel Stability Analysis with Seismic Load［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(6):1081－1088.(in Chinese))

［10］王 涛，陈晓玲，于利宏.地下洞室群围岩稳定的离散元计算［J］.岩土力学，2005，26(12):1936－1940.(WANG Tao，CHEN Xiao-ling，YU Li-hong.Discrete Element Calculation of Surrounding Rock Mass Stability of Underground Cavern Group［J］.Rock and Soil Mechanics，2005，26(12):1936－1940.(in Chinese))

［11］夏 祥，李俊如，李海波，等.爆破荷载作用下岩体振动特征的数值模拟［J］.岩土力学，2005，25(1):50－56.(XIA Xiang，LI Jun-ru，LI Hai-bo，et al.UDEC Modeling of Vibration Characteristics of Jointed Rock Mass Under Explosion［J］.Rock and Soil Mechanics，2005，25(1):50－56.(in Chinese))

［12］赵 坚，陈寿根，蔡军刚，等.用UDEC模拟爆炸波在节理岩体中的传播［J］.中国矿业大学学报，2002，31(2):111－115.(ZHAO Jian，CHEN Shou-gen，CAI Jun-gang，et al.Simulation of Blast Wave Propagation in Joined Rock Mass Using UDEC［J］.Rock and Soil Mechanics，2002，31(2):111－115.(in Chinese))