基于神经网络PID的电动汽车轮毂电机调速设计与仿真
2015-12-03杨世春田朋云
周 帆,徐 斌,杨世春,郑 嘉,田朋云
(1.北京航空航天大学交通科学与工程学院,北京 100083;2.华中科技大学机械科学与工程学院,武汉 430074)
轮毂式电动汽车电流回路中有很多的电感、电容等非线性元件,实际启动时这些元件对于启动初期的电流影响很大,使得启动信号并非“从0到1”的简单阶跃变化,而是一个不稳定的信号,所以电机控制系统应满足不稳定信号下的良好响应;同时电动汽车在运行过程中,路况等因素会对电机控制系统加入很多扰动,故还应满足随机信号扰动下能够实现转速稳定的能力.
多年来,很多学者对轮毂式电动汽车常用的无刷直流电机进行研究,提出了多种控制策略[1-5]:如双闭环PID控制、模糊控制以及神经网络控制等.神经网络具有大规模并行处理、容错性、自组织和自适应能力等特点[2],对控制技术瓶颈,更深入探索非线性系统控制起到了重大作用,已在很多工程领域取得了广泛应用[3].文中采用神经网络控制策略,构建满足上述需求的神经网络PID控制系统,并进行仿真验证.
1 无刷直流电机的数学模型
为方便分析,对无刷直流电机进行合理假设[1-3]:①忽略电机铁芯饱和,忽略涡流和磁滞损耗;②不计电枢反应,磁场分布近似认为是平顶宽度为120°电角度的梯形波;③忽略齿槽效应,电枢导体连续均匀分布于电枢表面;④任意时刻只有2相导通.本系统采用120°型三相逆变器,其简化图如图 1 所示[3].Ua,Ub,Uc为定子绕组相电压(V),ia,ib,ic为定子绕组相电流(A),ea,eb,ec分别为定子绕组相电动势(V),Ra,Rb,Rc为每相等效电阻,La,Lb,Lc为每相绕组的自感(H),M为绕组间互感(H).
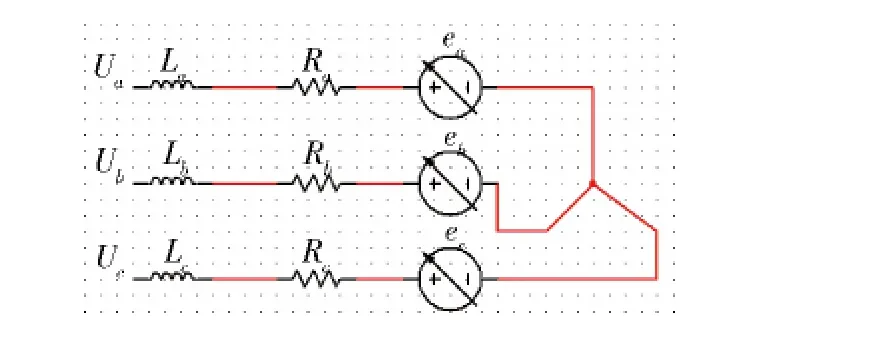
图1 无刷直流电机简化图
三相绕组的电压平衡方程为
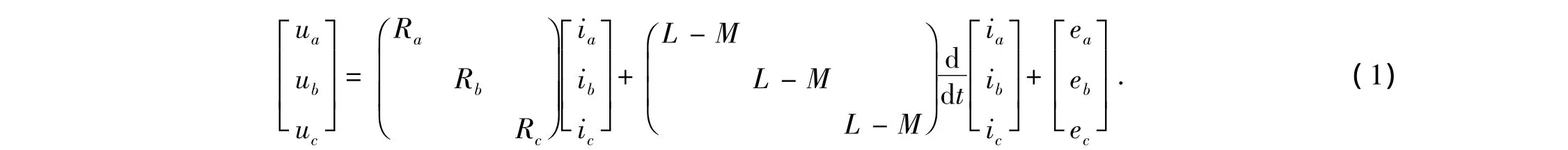
定子绕组产生的电磁转矩为
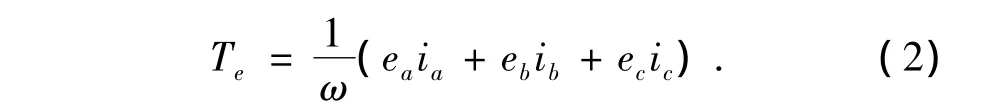
根据假设④,功率Pe为
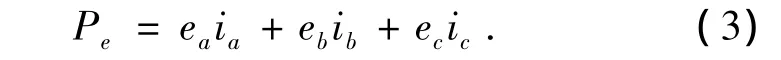
电磁转矩又可以表示为
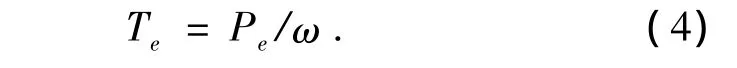
运动方程
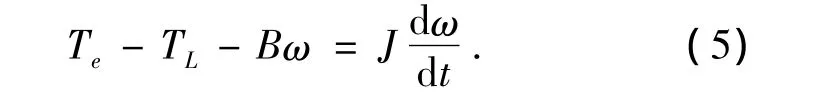
以上各式组成了无刷直流电机的数学模型[6],具体推导过程详见文献 [2,4].
2 传统PID无刷直流电机的调速原理
传统的PID控制算法[4-5]为

式中:误差e(k)=r(k)-y(k);r(k)为期望输出;y(k)为实际输出.
传统PID控制对于线性系统和简单的非线性系统具有较好的控制效果[7].轮毂式电动汽车的运转过程中,在启动信号恒定、路况良好的情况下,采用此种控制策略可以对输入信号进行很好的响应.实际过程中,输入信号以及路况等难以达到理想状态,电机的控制系统经常会在不稳定的启动信号 (随机信号)下开启,并且在运转过程中经常会受到各种不确定因素的扰动.一个典型的直流无刷电机的电流、转速双闭环PID控制 (下文简称传统PID控制)框图[8]如图 2 所示.
速度反馈回路采用的是脉冲测速,以达到适应微控制器的数字控制的目的,速度调节器的输出作为电流给定,电流检验经A/D变换后进入微控制器以形成电流反馈;由于无刷直流电机的电流波形为确定的矩形,所需控制的只是电流幅值,故采用PWM控制方式来实现.由于电磁转矩的大小与电流成正比,因此,可实现对转矩,进而对速度的闭环控制[3].
对于传统 PID电机调速、控制系统,在Matlab/Simulink环境下以阶跃信号和随机信号进行输入,得其响应曲线如图3所示.
由图3可以看出,传统PID电机控制对于随机信号的响应并不理想,在电动汽车中应用时很难达到要求.控制系统需要能够对不确定、非线性的因素能够实现较好的控制.

图2 直流电机双闭环PID控制框图
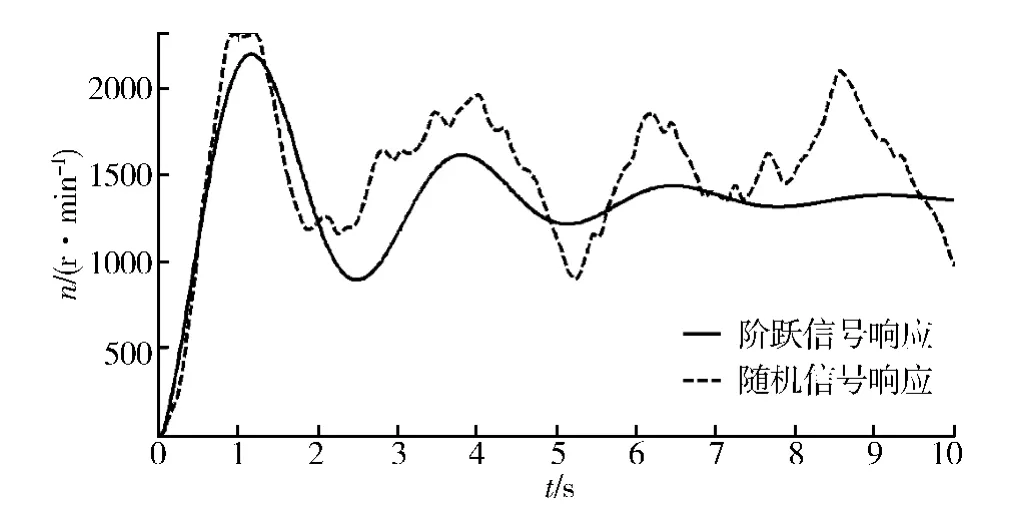
图3 传统PID电机系统对阶跃信号和随机信号的响应
3 神经网络模型的构建
神经网络具有任意逼近未知非线性系统的能力,能够对不确定、有复杂扰动的系统进行有效控制的目的[9].采用基于输出误差的神经网络辩识方法对被控对象进行辨识,其具体方法见文献[9]和 [10],在此基础上,设计神经网络PID控制系统,网络的权值向量为V=[v1,v2,v3],即表征PID控制器的3个参数kp,ki,kd,应用神经网络所具有的学习能力,神经网络PID控制能够实时在线计算修正控制参数以对系统或扰动的变化实现有效控制.
对应于 (6)式,神经PID的自适应线性神经元的输入为
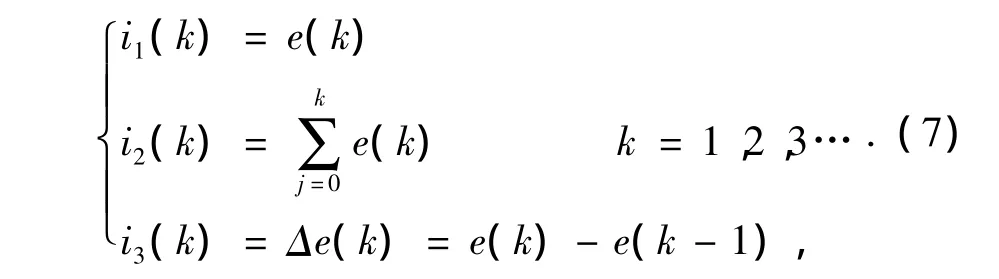
输出值为
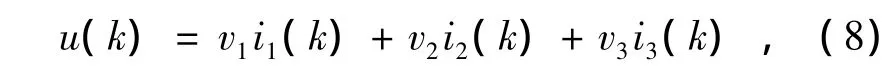
式中:vi是神经网络控制的权值,i=1,2,3.
目标函数为
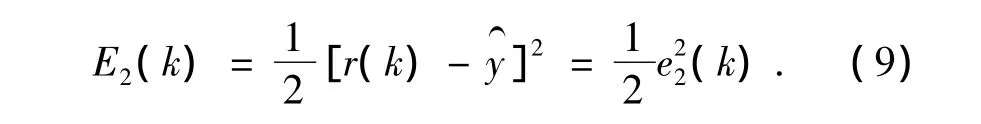
则网络权值调整算法为

完成上述分析后,即可在Matlab/Simulink中建立仿真模型.
4 系统仿真与结果分析
Matlab/Simulink提供了一个动态系统建模、仿真和综合分析的集成环境.
(1)搭建仿真模型
搭建神经网络模块,共设计13个隐层,以传统PID系统对阶跃信号的响应为目标输出,采用BP算法进行训练,训练结果如图4所示.
由图4可以看出,期望输出和神经网络控制系统的输出拟合度较好,可以较好的对目标输出进行跟踪,且平均误差小于3%,控制系统合理.
进行仿真验证.选取某型电机进行建模,其部分铭牌参数:λ=1.5;额定转速nN=1500 r/min,晶闸管放大倍数Ks=62.5;电枢回路总电阻R=0.863 Ω;电流反馈系数β=0.028 V/A;转速反馈系数 α =0.0041 V/(r·min-1).
在Simulink环境下搭建电机模型,具体搭建方法可以参见文献 [3],仿真模型如图5所示.
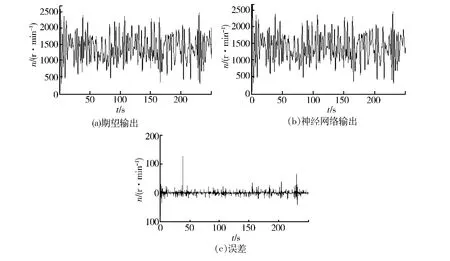
图4 神经网络控制模块训练结果

图5 Simulink仿真框图
(2)仿真结果与分析
对控制系统进行以下仿真:①传统PID控制系统和基于神经网络PID控制的电机控制调速系统对阶跃信号的响应情况,见图6;②随机信号输入(对应不稳定启动信号)下两种系统的响应情况,见图7;③以传统PID控制系统的阶跃响应为目标输出,在T=5 s时加入随机负载后,两种系统的响应对目标输出的跟踪情况,见图8.

图6 两种控制策略对阶跃信号的响应
图6可以看出,在阶跃信号激励下,两种控制系统的响应情况基本无差,神经网络PID控制系统的最大超调量较传统PID控制系统小4.21%,响应时间滞后约0.2 s,这是因为神经网络在初始时需在线计算控制参数造成的.

图7 随机信号下两种控制策略仿真
图7可以看出,神经网络PID控制在对不稳定信号的响应方面较传统PID控制对于随机响应方面有着较为明显的优势,此时传统控制策略的最大超调量较神经网络PID策略多5.12%,且神经网络控制系统的响应信号较为平稳,抗干扰能力较强.
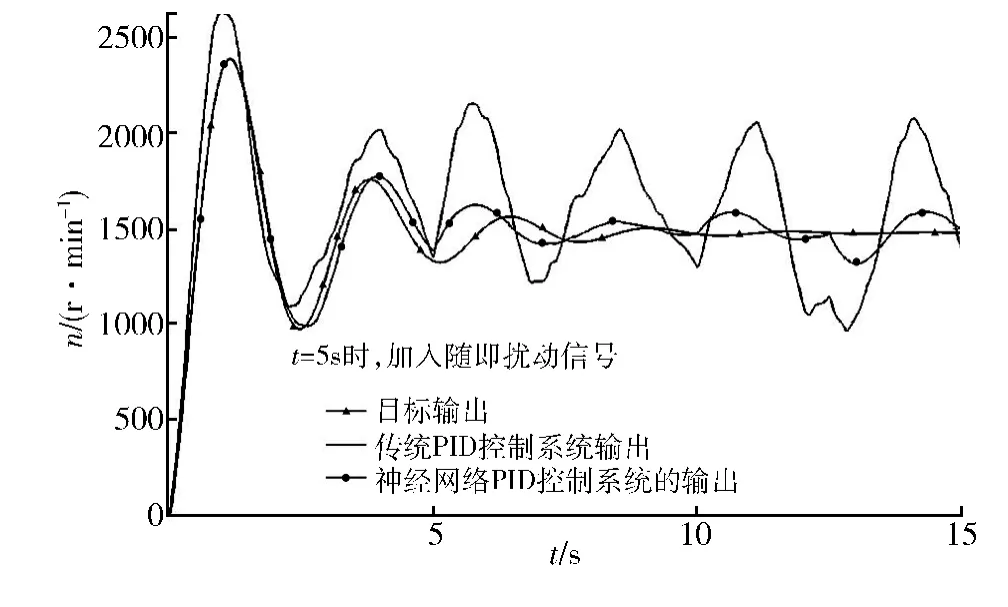
图8 t=5s加入随机扰动后两种策略的响应对目标输出追踪情况
从图8可以看出,神经网络PID策略在抗负载干扰方面有着明显的优势,在t=5 s加入随机扰动(变负载信号)后,传统PID控制策略的输出信号趋于不稳定状态,神经网络PID控制系统的输出信号在较小的波动后能马上恢复平稳,对于期望输出能够实现较好的跟踪,且最大误差为8.64%,可以满足一般行驶需求.
5 结论
采用神经网络控制电动汽车电机调速的策略相对于传统PID控制系统具有明显的优势,对一般阶跃信号,最大超调量可以降低4.21%,对不稳定信号超调量可以降低5.12%.且在不规则信号下的输出较为平稳,在受到扰动后能够较快的恢复稳定,最大误差小于8.64%,仿真结果表明采用神经网络控制策略对轮毂电动汽车电机进行控制具有合理性及可行性.
[1]杨向宇.直流无刷电机控制系统的建模与仿真[J].华南理工大学学报 (自然科学版).2005.8(33):28-32.
[2]胡闯,BP神经网络在无刷直流电机调速系统中的应用[D].武汉.华中科技大学硕士学位论文.2013.
[3]戴莹,基于BP神经网络的无刷直流电机PID控制方法的研究[D].合肥.合肥工业大学硕士学位论文.2007.
[4]徐岸非,无位置传感器永磁无刷直流电机控制系统研究[D],武汉,华中科技大学硕士学位论文,2006.
[5]卢东斌,四轮驱动电动汽车永磁无刷轮毂电机驱动系统控制研究[D],清华大学博士学位论文,2012.
[6]Pillay P,Krishnan R. Modeling,Simulation and Analysis of Permanent-Magnet Motor Drives.[J]IEEE Trans.Industry Application,1989,25(2):274-279
[7]胡寿松.自动控制原理[M].5版.北京:科学出版社.2007.
[8]薛定宇.基于MATLAB/Simulink的系统仿真技术与应用[M].2版.北京:清华大学出版社,2011.
[9]韩力群.智能控制理论及应用 [M].北京:机械工业出版社.2007.
[10]徐丽娜.神经网络控制[M].2版.北京:电子工业出版社,2009.
