基于集总参数法的坦克动力装置非稳态传热模型
2015-12-03赵以贤毕小平
赵以贤,毕小平
(1.装甲兵学院,蚌埠 233050;2.装甲兵工程学院,北京 100072)
为了大幅度提高主战坦克的战斗性能,对发动机功率密度和紧凑性的要求越来越高.我国几代主战坦克的发展,发动机功率成倍增加,而坦克动力舱的容积几乎未变,由此产生的严重问题是发动机的散热量不断增加,致使坦克动力舱内的传热问题越来越突出,这已经成为制约坦克发展的关键因素之一.为了保证坦克的正常工作,进行坦克动力装置传热性能研究十分必要.
过去的工作主要是针对设计工况进行简单的热平衡估算,然后通过实验的办法验证设计,消耗大量人力物力,而且有些关键参数受实验条件的限制难于测得.
坦克动力装置非稳态传热,是指坦克发动机处于非稳态工作时,动力装置 (包括冷却液、润滑油、燃油等)的温度、传热流量等随时间变化的传热过程.基于集总参数法,针对发动机部件、冷却系统、润滑系统和动力舱内的空气流动,建立了热力系统的综合非稳态传热模型.并对一台坦克动力装置非稳态传热进行了实例计算.
1 理论模型
1.1 动力装置非稳态传热的集总参数法
由于坦克动力装置结构的复杂性,要对其非稳态传热进行研究,采用一般的传热数值计算,无论人力还是计算机的容量都是难以承受的.在此我们采用集总参数法对坦克动力装置非稳态传热进行研究.
集总参数法解决传热问题,毕渥数BiV必须满足下列条件:

式中:M是与物体几何形状有关的无量纲数.
坦克动力装置的非稳态传热问题,要采用集总参数法求解,存在的问题是:坦克动力装置某些部件的非稳态传热的毕渥数BiV不满足集总参数法求解的限制条件;集总参数法是固体非稳态导热的一种计算方法,而坦克动力装置的非稳态传热,除了部件的非稳态导热以外,还包含冷却介质的非稳态传热;集总参数法主要解决单一部件的非稳态传热问题,而坦克动力装置的非稳态传热是许多部件及冷却介质组成的热力系统.
采用集总参数法求解坦克动力装置的非稳态传热问题,采取以下措施:
(1)将毕渥数BiV不满足集总参数法求解限制条件的动力装置某些部件进行网格划分,使离散后的单元非稳态传热的毕渥数BiV满足集总参数法求解的限制条件[1];
(2)对于冷却介质的非稳态传热,冷却介质与壁面的传热为对流换热,冷却介质自身的传热主要靠冷却介质的流动来实现,按照集总参数法求解固体非稳态导热的思路,以圆管为例,冷却介质自身的流动换热热阻为,冷却介质与壁面的对流换热热阻为,两者热阻的比可作为集总参数法求解冷却介质非稳态传热问题的限制条件,即
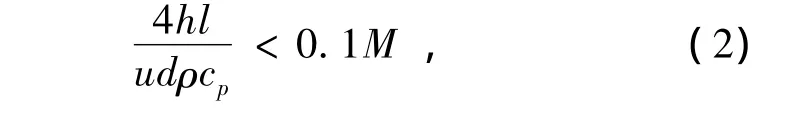
式中:h是冷却介质与壁面的对流换热系数,W/(m2·K);l是圆管的长度,m;u是冷却介质在圆管内的流速,m/s;d是圆管的直径,m.
(3)作为一个复杂的热力系统,要采用集总参数法求解其非稳态传热问题,虽然单元的热阻可以忽略,但系统的热阻则不能不考虑.为此,解决的办法是将局部热阻分别加到单元与单元之间的界面上.
1.2 活动边界的热耦合关系
在发动机工作过程中,气缸套内壁单元与活塞侧面单元的相对关系在发生变化,边界条件不确定,就难以进行计算.因此,需要研究气缸套内壁单元与活塞侧面单元的热耦合边界的变化规律.
活塞的位移是曲轴转角的函数,根据发动机的结构,可以求出活塞的位移

式中:R是曲柄半径,m;θ是曲轴转角,rad;λ是曲柄半径与连杆长度的比.
假定计算的时间步长为Δτ,当计算到第i步时,曲轴转角为
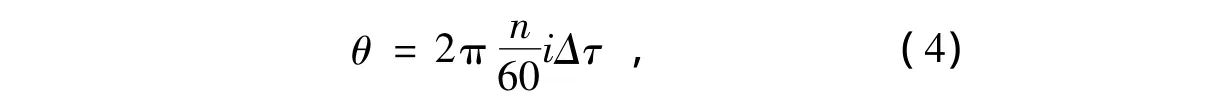
式中:n是发动机转速,r/min.
为了说明问题,假定沿气缸套的厚度方向(即半径方向)作 nq等份,每个等份的长度为Δyq,气缸套沿高度方向作ns等份,每个等份的长度为Δzs;沿活塞半径方向作nk等份,每个等份的长度为Δyk,活塞沿高度方向作nm等份,每个等份的长度为Δzm.
当sΔzs<S(θ)时,气缸套内壁单元cy(1,s)与燃气接触;
当 sΔzs> S(θ)+nmΔzm时,气缸套内壁单元cy(1,s)与润滑油接触;
当 S(θ)≤ sΔzs≤ S(θ)+nmΔzm时,气缸套内壁单元cy(1,s)与活塞某单元pi(1,m)接触.s与m满足下列关系:

式中:s是气缸套沿z方向的单元顺序数;m是活塞沿z方向的单元顺序数;δ是单元偏离控制量,m.
1.3 动力装置单元非稳态传热控制方程
动力装置非稳态传热控制单元分为固体控制单元与液体控制单元.
动力装置第(j,k)固体单元非稳态传热控制方程的一般形式[2]为
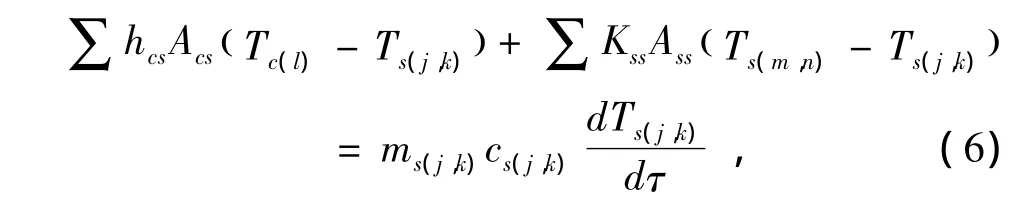
式中:hcs是第(j,k)固体单元与流体 (包括燃烧气体)的对流换热系数,W/(m2·K);Acs是第(j,k)固体单元与流体接触的面积,m2;Kss是第(j,k)固体单元与相邻固体单元的传热系数,W/(m2·K);Ass是第(j,k)固体单元与相邻固体单元接触的面积,m2;角标s(j,k)代表第 (j,k)固体单元;角标s(m,n)代表与第(j,k)固体单元相邻固体单元;c是材料的比热,kJ/(kg·K);T是单元的温度,K;角标c(l)代表与第(j,k)固体单元相接触的某种流体.
动力装置第c(l)液体单元非稳态传热控制方程的一般形式[2]为
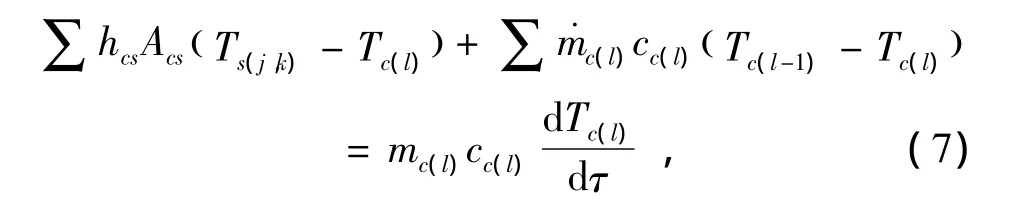
式中:m是液体单元的质量,kg;˙mc(l)是两个单元之间液体的质量流量,kg/s.
燃烧气体与燃烧室壁面之间的对流换热系数应用 Woschni公式[3]计算.
固体部件与冷却液、润滑油之间的对流换热是强制对流换热,对流换热系数根据流体流动的形态分别采用层流或湍流公式[4]进行计算.
新鲜空气与发动机进气系统、压气机、中冷器之间进行换热,废气与发动机排气系统、涡轮之间进行换热.其换热系数应用顾宏中的经验公式[5]计算.
动力装置的外表面与动力舱空气之间进行对流换热及辐射换热,其换热系数应用Krishna推荐的公式[6]计算.
1.4 求解策略
动力装置非稳态传热问题的求解,应合理地确定初始条件和边界条件.另外,由于动力装置非稳态传热问题的特殊性,有些单元,其控制方程并不唯一,需要研究各控制方程的时效性.对于显示差分方程解的稳定性问题,需要研究动力装置非稳态传热显示差分格式的限制条件.
1.4.1 初始条件及边界条件
环境温度为20℃、大气压力为101.325 kPa,动力装置所有部件、冷却液、润滑油、燃油等的温度的初始值与环境温度一致.为了分析问题的方便,忽略发动机起动的一瞬间,假定发动机一开始就处于2200 r/min的标定功率下工作,这相当于有载荷下的加温过程.
动力装置与动力舱内空气的换热流量,不但与动力装置本身的温度有关,还与动力舱内空气的流动状态及温度有关,在动力装置非稳态传热计算时,动力舱内空气的流动状态及温度需要提前给定.在计算中,应用“坦克动力舱热工况建模、仿真和空气流动测试研究”中动力舱空气流动数值模拟结果作为动力装置非稳态传热计算的边界条件,每计算一步,均对应一组边界条件.
1.4.2 非稳态传热控制方程的资格认定
非稳态传热问题的求解过程,就是将求解区域内的每个单元对应的非稳态传热控制方程进行离散,形成一组代数方程,在每个时间步上求解代数方程组.但对于坦克动力装置非稳态传热问题,气缸套内壁单元和活塞侧面单元,它们的非稳态传热控制方程并不唯一,也就是说,气缸套内壁的每一个单元的非稳态传热控制方程有多种形式,活塞侧面的每一个单元的非稳态传热控制方程也有多种形式.但在每个求解时间步上,每一个单元的非稳态传热控制方程的形式又是确定的,即非稳态传热控制方程是唯一的.这样,在非稳态传热问题的求解过程中,对于每个求解时间步,都需要对非稳态传热控制方程不唯一的单元,确定其非稳态传热控制方程的形式.这个过程,我们称之为传热控制方程的资格认定.
1.4.3 非稳态传热控制方程的离散化 采用显式差分格式,式 (6)的离散形式[2]为
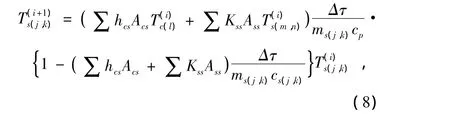
式中;Δτ为时间步长,s;上角标i是时间层.
采用显式差分格式,式 (7)的离散形式[2]为
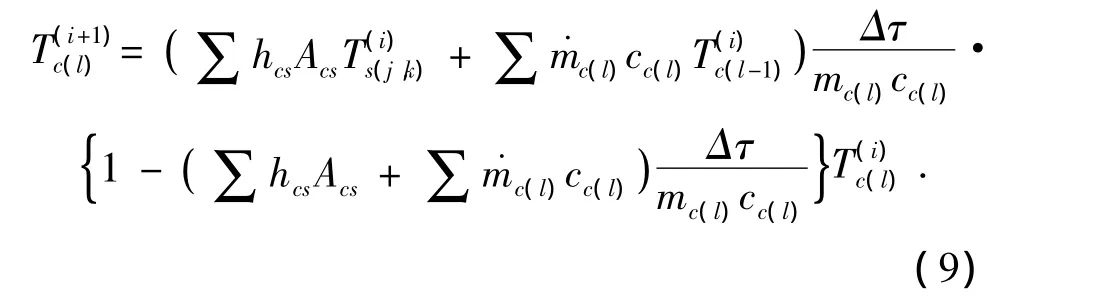
1.4.4 非稳态传热显式差分的限制条件
式 (8)和式 (9)的物理意义是很明显的,单元i+1时刻的温度是在该单元i时刻温度的基础上计及了相邻单元温度的影响后得出的.假如相邻单元的影响保持不变,合理的情况是:i时刻该单元的温度越高,则其相继时刻的温度也较高;反之,i时刻该单元的温度越低,则其相继时刻的温度也较低.
在差分方程中,要满足解的合理性是有条件的,对于固体单元,式 (8)中T(i)s(j,k)前的系数必须大于或等于零,即

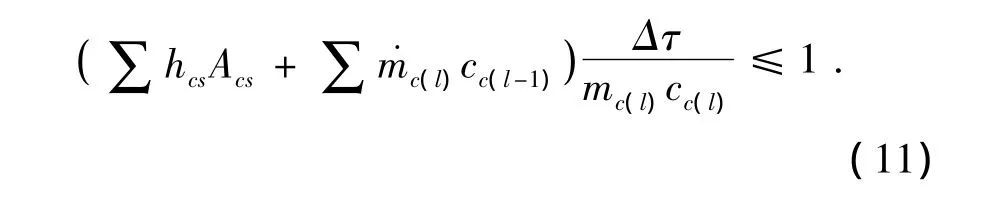
2 计算结果
对某型坦克动力装置的非稳态传热进行了仿真,其结果非常丰富.这里主要分析动力装置主要部件向动力舱的散热量、发动机主要部件的温度分布及其随发动机工作时间的变化关系等.
2.1 动力装置主要部件的散热流量
图1为发动机主要部件向动力舱的散热流量随时间的变化关系.
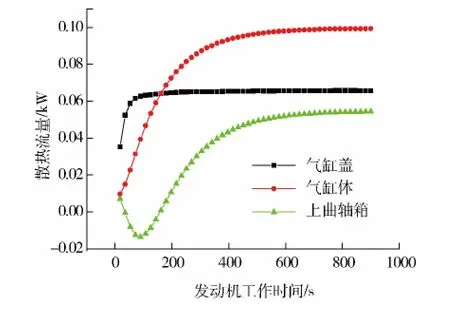
图1 发动机主要部件向动力舱散热流量的试件历程
各部件向动力舱的散热流量趋于各自稳定值的时间不同,气缸盖向动力舱的散热流量比较早地达到稳定值,而排气歧管向动力舱的散热流量达到稳定值的时间比较晚.造成这种现象有两个原因:一是气缸盖与燃气的换热比排气歧管与废气的换热要强烈;二是排气歧管的温度要比气缸盖的温度高的多.上曲轴箱在开始阶段,其散热流量为负值.这主要是由于上曲轴箱不直接与燃气接触,其温度上升比较缓慢,而上曲轴箱周围空气的温度已超过上曲轴箱的温度,在此阶段上曲轴箱的散热流量为负值.
图2为水散热器的散热流量随时间的变化关系,图3为机油散热器的散热流量随时间的变化关系.
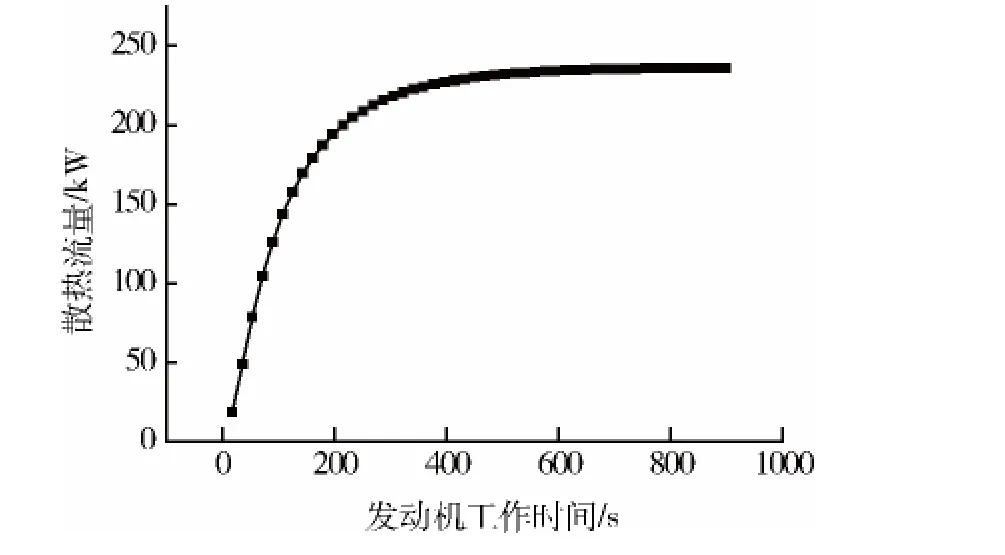
图2 水撒热器的散热流量的试件历程
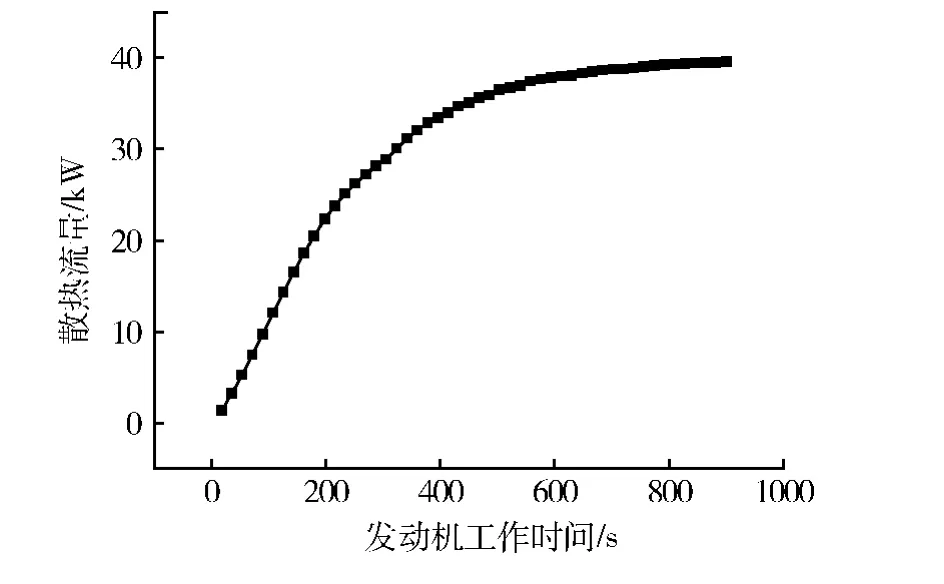
图3 机油散热器的散热流量的试件历程
从图中可以看出,水散热器的散热流量和机油散热器的散热流量均随发动机工作时间的增加而增加,当发动机工作到一定时间以后,其散热流量趋于各自的稳定值,水散热器的散热流量趋于稳定值的时间要早于机油散热器.这主要是由于发动机部件与冷却液的换热比发动机部件与润滑油的换热要强烈.
2.2 发动机主要部件的温度
图4为发动机有关部件温度随时间的变化关系.从图中可以看出,气缸体、气缸盖本体 (不含燃烧室及排气道)及连杆的温度,在发动机工作的200 s内,变化较大;发动机工作200 s以后,气缸体、气缸盖及连杆的温度变化非常缓慢.但排气歧管的温度在发动机工作900 s以内,变化仍然较大.且温度也是最高的.这是由于排气歧管与管内废气的换热强度比气缸内燃气与壁面的换热强度要低,而且排气歧管趋于稳定温度的值也比较高.
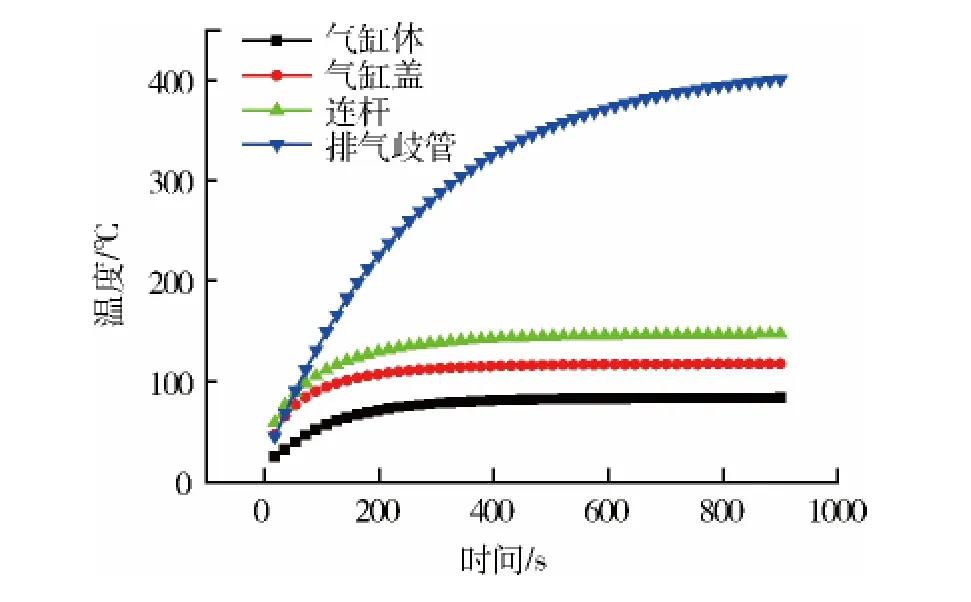
图4 发动机主要部件的温度的试件历程
图5为发动机工作180 s时气缸套的温度分布情况.
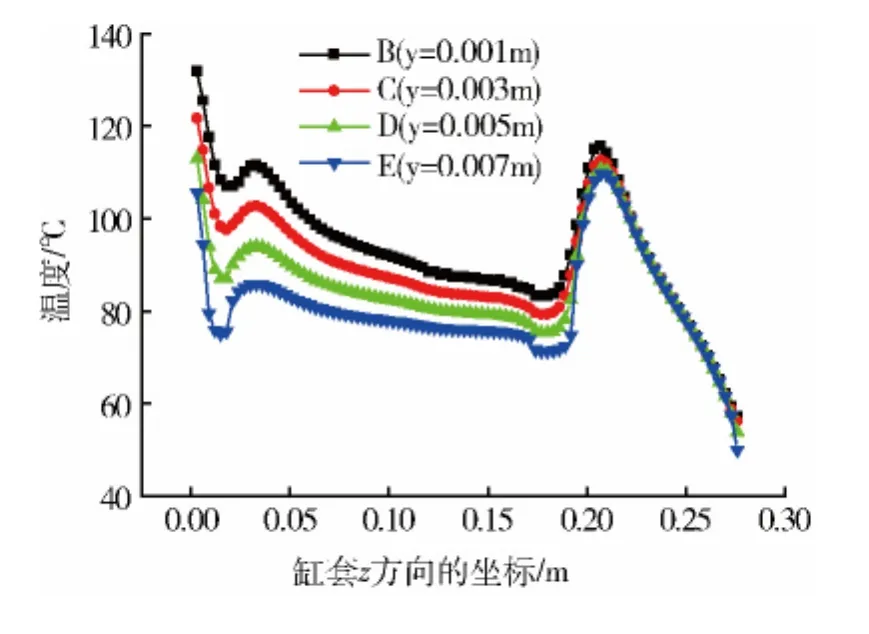
图5 发动机工作180 s时气缸套的温度发布
图中位于上方的曲线为气缸套内壁各单元的温度;位于最下方的曲线为气缸套外侧各单元的温度.就每条曲线而言,靠近气缸盖的单元,其温度较高.气缸套的中间部分,其外侧与冷却液接触,换热比较强烈,因此,该部分的各单元温度较低.气缸套的最下面部分,没有水道,仅靠润滑油散热.由于气缸套与润滑油的换热比气缸套与冷却液的换热要弱得多,该部分各单元的温度较高,这就是曲线右侧出现山峰的原因.就某一部分而言,如气缸排水道附近的各单元,随坐标z的增加,单元的温度在减小.远离燃烧室的各单元,与燃气接触的时间相对要短一些,与燃气的平均换热流量也要小一些,其温度也要相对低一些.
3 结论
发展了一个基于集总参数法的坦克动力装置非稳态传热模型,并经一台坦克动力装置非稳态传热的实际应用,显示该模型能够全面考虑影响传热性能的各种因素及其相互耦合关系,得到大量有用数据,其中很多是实际测试得不到的数据,因此可以用于坦克动力装置非稳态传热的研究.
[1]赵以贤,毕小平等.基于集总参数法的车用内燃机传热计算机仿真研究[J].内燃机学报,2003,21(4):239-243.
[2]赵以贤,毕小平.坦克动力装置综合传热建模与仿真[M].北京:军事科学出版社,2007:169-198.
[3]Woschni G.A Universally Applicable Equation for the Instantaneous Heat Transfer Coefficient in the Internal Combustion Engine. SAE Technical Paper 670931,1967,DOI:10.4271/670931.
[4]杨世铭,陶文铨.传热学[M].3版.北京:高等教育出版社,1998.
[5]顾宏中.涡轮增压柴油机热力过程模拟计算 [M].上海:上海交通大学出版社,1985.
[6]Krishna V M,Oner A,Song L Y,et al.A computer simulation of the turbocharged diesel engineas an enhancement of zhe vehicle engine cooling system simulation.In:SAE Paper[C].1997,971804.
