高速轴承动力学有限元分析方法

张 利， 祁华铭， 徐 娟， 吉智军

(1. 合肥工业大学机械与汽车工程学院，安徽 合肥 230009；2. 合肥工业大学安全关键工业测控技术教育部工程研究中心，安徽 合肥 230009；3. 洛阳轴研科技股份有限公司，河南 洛阳 471039)

高速轴承动力学有限元分析方法

张 利1， 祁华铭1， 徐 娟2,3， 吉智军3

(1. 合肥工业大学机械与汽车工程学院，安徽 合肥 230009；2. 合肥工业大学安全关键工业测控技术教育部工程研究中心，安徽 合肥 230009；3. 洛阳轴研科技股份有限公司，河南 洛阳 471039)

高速轴承是高速列车安全运行的重要部件，轴承运转过程中的动态特性直接影响轴承的使用寿命，采用最小部件之间创建面面接触的方式，建立高速轨道客车用双列圆锥滚子轴承的三维虚拟样机模型，利用ANSYS/LS-DYNA分别研究客车直线匀速行驶和额定速度下以最小转弯半径行驶两种工况下轴承运转过程的动态接触特性，得到轴承的速度特性、加速特性以及滚子承载分布状况、接触单元法向作用力时间历程变化曲线以及保持架的振动曲线，研究结论可以为高速轴承设计过程中模型构建方案的合理确定提供参考。

动力学；虚拟样机；ANSYS/LS-DYNA；高速轴承

高速铁路客运是未来铁路客运发展的方向， 随着铁路运行的不断提速，性能良好的高速轴承

将大量应用。提高轴承的性能与寿命，对提高整车的动力性、安全性和操纵稳定性起着至关重要的作用，因此分析轴承运转中各部件速度、加速度和位移量、应力等的变化和分布情况，并根据受力情况判断易发生疲劳破坏和失效的部位而指导设计过程[1-5]，优化结构参数就显得尤为重要。通常轴承是在动态载荷工况下工作，滚动轴承的动态接触特性是轴承组件间的复杂动力学行为和接触力学行为的综合体现[3]。

近年来，有关机械零部件间动态接触特性的研究已成为轴承数值分析领域的研究热点。在滚动轴承运转过程中的动态接触特性数值仿真分析领域已有许多研究。如徐弘毅和张晨辉[4]对采用线弹性材料模型和塑性材料模型的情况进行了对比分析，其结果证明材料模型对数值仿真结果产生影响；李国超等[6]应用 ANSYS/LS-DYNA建立轴承外圈裂纹故障模型，成功地对外圈裂纹故障进行了仿真分析；樊莉等[7]利用了ANSYS/LS-DYNA实现了对滚动轴承运动过程中的三维数值模拟，探讨了滚动体接触应力的变化规律；林腾蛟等[8]在 ANSYS中建立深沟球轴承动力接触有限元模型，采用显示动力学有限元法对该轴承进行动态接触分析，求解了轴承的位移速度、加速度及滚动体单元应力。

考虑到滚子母线的修型、接触部件的网格细化、表面单元的模拟、最小转向半径的等效载荷状况，运用有限元方法建立双列圆锥高速铁路轴承多体动力学分析模型，通过分析比较得到了轴承的动态特性，为高速轴承的优化设计提供了参考。

1 分析基础

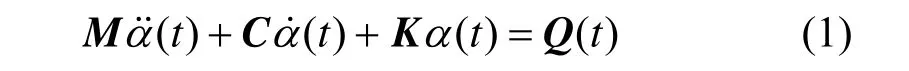
在滚动轴承动态接触特性的有限元数值分析过程中[9-10]，轴承系统的求解方程为：式中， α( t)、 α˙(t )、 α˙(t )分别是节点的位移向量、速度向量和加速度向量；M为系统的质量矩阵，C为阻尼矩阵，K为刚度矩阵，Q(t)为系统的节点载荷矩阵。

在该动力平衡方程中，考虑了惯性力和阻尼力的影响。因此，最后的求解方程是包含有质量矩阵和阻尼矩阵的常微分方程组。

ANSYS/LS-DYNA采用直接积分法的中间差分对运动方程积分求解。利用中心差分法，速度和加速度可以用位移表示为：

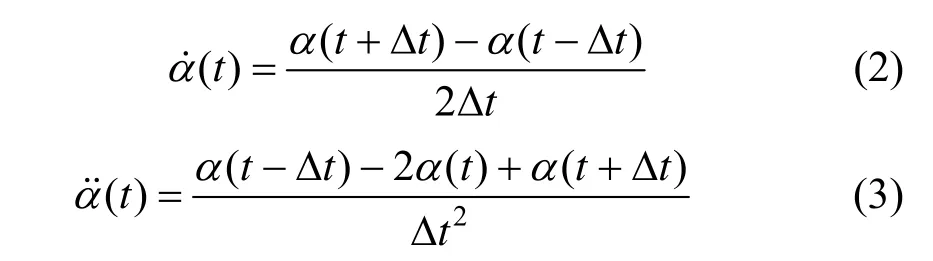
联立式(1)～(3)，可得到各个离散时间点位移的递推公式为：

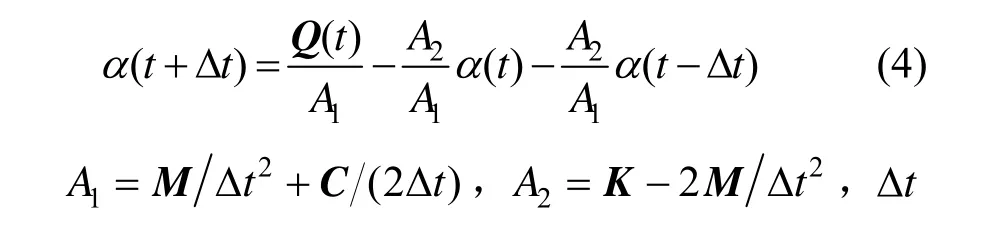
为求解时间步长。

给定单元运动的初始条件，可利用式(4)求解单元节点在某一个时刻的位移值，进而根据位移值计算得到加速度、应力、应变等。

建立准确的三维模型是确保有限元模拟准确的关键性因素[2]，为真实地反映轴承各部件的受力情况，取轴承整体模型进行动力学分析，保留机构的各个细节如保持架兜孔的倒角、滚子母线的修型及保持架与兜孔之间的间隙等。

各部件的材料属性[3-7]如表1所示。

表1 部件材料属性

2 有限元模型

本文对双列圆锥滚子轴承的外圈、内圈、保持架、中隔圈和滚子进行三维几何建模，导入有限元软件ANSYS中划分网格、设置边界条件、施加载荷，构成分析所必须的有限元模型。在保证准确反映接触情况的前提下，综合考虑网格数量和计算时间，选择接触面和设定接触区网格尺寸。

2.1 网格划分

网格尺寸的选择参考文献[11]。为准确反映接触应力，接触面网格单元尺寸应小于静力接触矩形的宽度，取接触面网格尺寸为接触矩形宽度的一半。为减少网格数量和计算时间，需要对网格进行合理的疏密布局，由于在动力学模型中静力接触矩形所在的全部弧面均为潜在的接触区，因此需先将模型进行切分，其深度为静力接触矩形宽度的一半，即接触区单元尺寸，从而建立了以接触面为边界的接触体区域(接触部件)，接触部件网格按静力接触矩形宽度的一半细化，非接触部件区域网格可粗略划分。

2.2 边界条件及约束

轴承外圈与固定轴承座联接，因此约束了全部自由度；内圈与轴联接，只能随轴转动和移动，因此约束X、Y旋转自由度；由于ANSYS/LS-DYNA中，SOLID164实体单元不具有旋转自由度，因此将轴承内圈表面定义为SHELL163单元[7]，以便施加转速和载荷进行动力分析。转速以及载荷施加在由SHELL163单元构成的内圈内表刚性面上，载荷施加方式ROZ，RFX，RFY。

接触类型设置为自动面面接触(auto surface to surface，ASTS)，允许接触出现在接触壳元的两侧，摩擦接触基于库仑公式。待轴承运转稳定后，不考虑因润滑脂干燥或其他因素引起的摩擦因数衰减系数，只考虑轴承实际的摩擦因数、润滑油和挡边等情况，建立摩擦因数，设置轴承在运转过程中滚动体与内外圈滚道的静摩擦因数为 0.1，动摩擦因数为 0.08；滚动体与保持架的静摩擦因数为 0.1，动摩擦因数为0.05。

面面接触建立于接触部件与目标部件之间，选取滚子表面节点建立为接触部件，选取内圈沟道表面节点、外圈沟道表面节点、保持架兜孔表面节点建立为目标部件，在定义接触部件与目标部件之间的接触参数时，要确保接触部件单元和目标部件单元不发生重叠以免产生穿透。有限元模型如图1所示。

图1 有限元模型

2.3 载荷条件

载荷条件分为受力载荷条件和速度载荷条件，要考察的工况为：

工况一：车辆在直道上行驶，轴承受到的是轴承箱和齿轮输出轴重力引起的径向载荷，其稳定转速为2 140 r/min，径向载荷为7.5 t。

工况二：车辆以最小转弯半径转向，轴承承受的径向载荷为7.5 t，轴向载荷为3.75 t。

3 计算结果及分析

基于ANSYS前处理器建立的轴承有限元模型提交LS/DYNA求解器求解，进行两种工况下的轴承动态分析，并将结果载入后处理模块 LS-Prepost中，得到轴承在两种工况下的速度和载荷曲线。

(1) 图 2(a)、(b)所示为内圈端面最大半径边缘处的速度和加速度曲线，可以看到在很短的时间内，内圈初始速度由0加速到额定值，之后呈现出一种锯齿状的波动。加速度的变化则在启动阶段较为剧烈之后趋于平稳。根据运动学理论[9-10]，保持架转动平稳后的速度曲线是一条平直线，但在实际中，保持架与钢球之间存在动态接触和碰撞，所以仿真计算得到的曲线并非是平直的，而稍微有所波动，说明仿真计算结果能更好地描述轴承的动态性能。

(2) 图 3(a)、(b)所示为某滚子中心及滚子半径边缘对应点的速度和加速度曲线，与内圈的启动到运转稳定相比，滚子的自转滞后于公转。当自转形成后，滚子边缘的速度为自转速度与公转速度的合成，速度曲线呈现出围绕中心的正弦波动，与文献[9]相符。加速度曲线呈现出一种抖动，其产生源于保持架与滚子的碰撞。

(3) 图4(a)为工况一t = 0.03 s时的应力分布，

图4(b)为工况二t = 0.03 s时的应力分布。当轴向分力与载荷方向一致的滚子组被压紧，另外一组滚子相对释放，使应力分布呈现一种偏载，与文献[9]中轴承作用载荷引起的球和滚子载荷中提出的偏载理论相符，轴向负载的增大将会加剧滚子偏载现象。

(4) 图5(a)为单元244498的应力变化曲线，单元的初始位置在轴承下半圈，轴承的承载区为下半圈，上半圈接触应力的形成来自于保持架与滚子的碰撞以及轴向受载产生的法向分力。保持架与滚子组的碰撞情况可以通过保持架质心振动的情况得到体现，如图5(b)所示。当保持架兜孔与滚子间隙为0.2 mm时，保持架质心最大振动量为0.5 mm；当保持架兜孔与滚子间隙为0.1 mm时，保持架质心最大振动量为0.2 mm。相比可以看出，减小间隙可以缓解保持架的振动，这与文献[12]分析吻合。保持间隙为0.1 mm，将每列滚子个数增加2个，此时保持架最大振动量降至0.08 mm，表明增加滚子的数量可以缓解保持架的振动，从而降低保持架与滚子间的冲击应力。

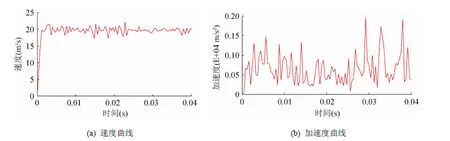
图2 内圈运转

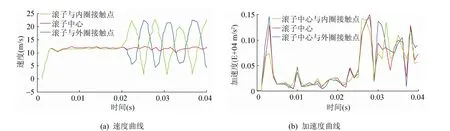
图3 某滚子中心与滚子边缘运转

图4 内圈承载分布

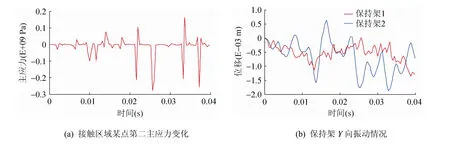
图5 接触区主应力与保持架振动

4 结 论

本文通过建立虚拟样机模型[13-14]，进行高速轴承动力学的有限元仿真分析，研究了轴承的运转特性、偏载和保持架振动情况，得到如下结论：

(1) 在正常直线行驶和最小转弯半径工况下，由于滚子母线的对数曲线修型，未出现显著的应力集中，但在转弯的过程中会出现偏载，极端情况为仅有一列滚子受载，使两列滚子疲劳寿命不均匀。

(2) 影响保持架振动量的主要因素为保持架兜孔与滚子间的间隙和滚子的数量，滚子数量的增加可减小应力的平均水平，减小间隙可改善保持架的振动情况。

(3) 该有限元法较真实地反映了轴承实际工作情况，可为改进提供依据，也可代替实物实验。尤其是针对可能出现的外圈沟道点蚀及保持架断裂等情况，该有限元法可作为改进滚子母线修型和保持架兜孔间隙效果的验证。

[1] 关 猛, 王景华, 牛清波, 等. 高速重载轴承的有限元仿真研究[J]. 合肥工业大学学报： 自然科学版, 2013, 36(5)： 527-530.

[2] 梁 佳, 雷基林, 申立中, 等. 某卧式柴油机体的有限元分析[J]. 汽车工程, 2012, 34(2)： 120-123.

[3] 童宝宏, 刘 颖, 苏 荭. 滚动轴承动态接触特性数值模拟中若干问题[J]. 机械工程学报, 2012, 48(21)： 116-123.

[4] 徐弘毅, 张晨辉. 基于塑性材料模型的滚动轴承有限元分析[J]. 机械工程学报, 2010, 46(11)： 29-35.

[5] Xu Dong, Huang Jinʹe, Zhu Qin, et al. Residual fatigue life prediction of ball bearings based on paris law and RMS [J]. Chinese Journal of Mechanical Engineering, 2012, 25(2)： 320-327.

[6] 李国超, 彭 炜, 李勇才, 等. 滚动轴承外圈故障的显示动力学有限元动态仿真分析[J]. 中国机械工程, 2012, 23(23)： 2825-2829.

[7] 樊 莉, 谭南林, 沈栋平. 基于显示动力学的滚动轴承接触应力有限元分析[J]. 北京交通大学学报, 2006, 30(4)： 109-112.

[8] 林腾蛟, 荣 崎, 李润方, 等. 深沟球轴承运转过程动态特性有限元分析[J]. 振动与冲击, 2009, 28(1)： 118-122.

[9] Harris T A, Kotzalas M N. 滚动轴承分析[M]. 5版. 罗继伟, 马 伟, 杨咸启, 译. 北京： 机械工业出版社, 2009： 160-280.

[10] 万长森. 滚动轴承的分析方法[M]. 北京： 机械工业出版社, 1987： 96-109.

[11] Xu Juan, Niu Qingbo, QI Huaming, et al. A research on the contact stress of roller bearing based on crowning analysis [J]. Computer Aided Drafting, Design and Manufacturing, 2012, 22(2)： 55-58.

[12] 刘秀海, 邓四二, 滕弘飞. 高速圆柱滚子轴承保持架运动分析[J]. 航空发动机, 2013, 39(2)： 31-38.

[13] 杨 勤, 赵慧亮, 赵冠浩, 等. 基于ANSYS的智能换电小车底盘结构静态分析[J]. 图学学报, 2014, 35(1)：37-41.

[14] 王恒亮, 陆正刚, 孙效杰, 等. 基于虚拟样机技术的铁路货车轴端电机结构设计[J]. 图学学报, 2013, 34(4)：105-111.

Finite Element Analysis of Dynamics of High Speed Bearing

Zhang Li1, Qi Huaming1, Xu Juan2,3, Ji Zhijun3
(1. School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei Anhui 230009, China; 2. Engineering Research Center of Safety Critical Industry Measure and Control Technology, Ministry of Education, Hefei University of Technology, Hefei Anhui 230009, China; 3. Luoyang Bearing Science & Technology Co. Ltd., Luoyang Henan 471039, China)

High speed bearings are key components for safe operation of high-speed train. There is a close relationship between rolling contact behavior and the service life of roller bearing. A 3D virtual model for high speed railway double row tapered roller bearing is established using automatic surface to surface contact between minimum component, and a finite element analysis of dynamic contact characteristics of the bearing under straight-line driving and minimum radius steering under scheduled velocity is conducted respectively using ANSYS/LS-DYNA. Speed, acceleration of bearing, load distribution of roller, time-history curve of contact element about second principal stress and vibration of holder is studied. The results can serve as reference in design and construction of high speed bearing.

dynamics; virtual model; ANSYS/LS-DYNA; high speed bearing

TH 133.3

A

2095-302X(2015)04-0546-05

2014-11-24；定稿日期：2015-01-12

国家国际科技合作资助项目(2013DFB70350)；教育部人文社会科学研究专项资助项目(工程科技人才培养研究：12JDGC007)；安徽省自然科学基金资助项目(1408085QE99)

张 利(1955–)，女，安徽蚌埠人，教授，硕士，硕士生导师。主要研究方向为机电一体化、汽车电子和网络化协同设计。E-mail：77zhangli@hfut.edu.cn