三特点阐释近几年全国高考新课标1卷

蒋振滨

2016年全国高考新课标1卷参考省份越来越多，作为一线教师，认真细致地研究新课标1卷是必做的功课，认真研读近5年试卷，从中我们可以感悟到新课标1卷的许多特点.

近几年来，全国新课标1卷理科试题难度较为稳定，题型稳中求变，没有难题和怪题，试题结构仍为12+4+5再加3选1，方法上灵活多变又不失本质.注重考查学生的五大能力、两个意识，即空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力、应用意识和创新意识；注重考查数学的基础知识、基本技能、基本思想方法，在试卷表述形式上力求简洁，方法考查上力求回归本质，在新增内容算法的考查上，把最基本的数据处理的统计知识作为考查对象，删减繁琐的计算，摒弃人为技巧化的难题，克服双基异化倾向，符合新课程标准的要求，本文就新课标卷的试题特点、思想方法、选拔功能做些探究.

1 试题结构的简洁美

简洁美体现在试题形式的一目了然，却又不失方法考查的深刻性，一道好题，不在试题本身的“山路十八弯”，应让学生一看便知，想去做、会去做，但要做对做全，却又不太容易，如2014年高考试题的第11题.题目：已知函数f（x）=ax3-3x2+1，若f（x）存在唯一的零点x0，且x0>0，则a的取值范围是（ ）.

A.（2，+∞） B.（1，+∞） C.（-∞，-2） D.（-∞，-1）

解 当a=0时，f（x）=-3x2+1=0，解得x=±3[]3[SX）]，函数f（x）有两个零点，不符合题意，应舍去；

当a>0时，令f′（x）=3ax2-6x=3ax（x-2[]a[SX）]）=0，解得x=0或x=2[]a[SX）]>0，列表如下：

f′（x）+0-0+

f（x）单调递增极大值单调递减极小值单调递增

因为x→+∞，f（x）→+∞，而f（0）=1>0，所以存在x<0，使得f（x）=0，不符合条件：f（x）存在唯一的零点x0，且x0>0，应舍去.

当a<0时，f′（x）=3ax2-6x=3ax（x-2[]a[SX）]）=0，解得x=0或x=2[]a[SX）]<0，列表如下：

f′（x）-0+0-

f（x）单调递减极小值单调递增极大值单调递减

而f（0）=1>0，x→+∞时，f（x）→-∞，所以存在x0>0，使得f（x0）=0，

因为f（x）存在唯一的零点x0，且x0>0，所以极小值f（2[]a[SX）]）=a（2[]a[SX）]）3-3（2[]a[SX）]）2+1>0，化为a2>4，因为a<0，所以a<-2.

综上可知：a的取值范围是（-∞，-2）.

故选：C.

本题题干简洁，给出的函数是学生所熟知的三次函数，让学生有做好本道试题的心理准备，但要做好做对它，却有些难，因参数位置在立方项系数，需分类讨论方能品味其内涵，这样的试题能多方向、多角度的考查学生的各种思维品质，给出的函数让人欢喜让人忧，简洁而又不简单.

又如2014年的第12题：

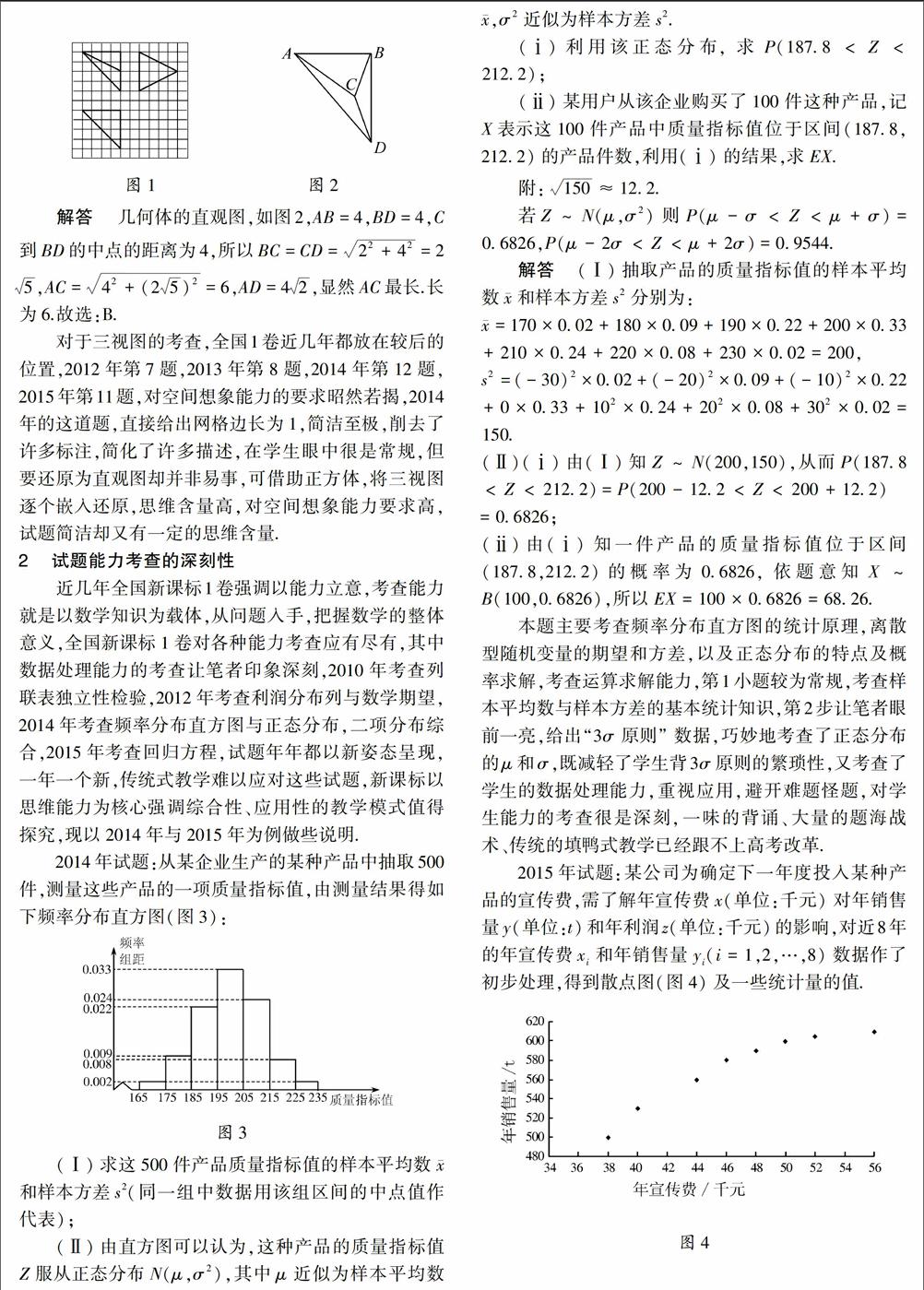
如图1，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）.

A.62[KF）] B.6 C.42[KF）] D.4图1 图2

解答 几何体的直观图，如图2，AB=4，BD=4，C到BD的中点的距离为4，所以BC=CD=22+42=25[KF）]，AC=42+（25[KF）]）2[KF）]=6，AD=42[KF）]，显然AC最长.长为6.故选：B.

对于三视图的考查，全国1卷近几年都放在较后的位置，2012年第7题，2013年第8题，2014年第12题，2015年第11题，对空间想象能力的要求昭然若揭，2014年的这道题，直接给出网格边长为1，简洁至极，削去了许多标注，简化了许多描述，在学生眼中很是常规，但要还原为直观图却并非易事，可借助正方体，将三视图逐个嵌入还原，思维含量高，对空间想象能力要求高，试题简洁却又有一定的思维含量.

2 试题能力考查的深刻性

近几年全国新课标1卷强调以能力立意，考查能力就是以数学知识为载体，从问题入手，把握数学的整体意义，全国新课标1卷对各种能力考查应有尽有，其中数据处理能力的考查让笔者印象深刻，2010年考查列联表独立性检验，2012年考查利润分布列与数学期望，2014年考查频率分布直方图与正态分布，二项分布综合，2015年考查回归方程，试题年年都以新姿态呈现，一年一个新，传统式教学难以应对这些试题，新课标以思维能力为核心强调综合性、应用性的教学模式值得探究，现以2014年与2015年为例做些说明.

2014年试题：从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图（图3）：图3

（Ⅰ）求这500件产品质量指标值的样本平均数和样本方差s2（同一组中数据用该组区间的中点值作代表）；

（Ⅱ）由直方图可以认为，这种产品的质量指标值Z服从正态分布N（μ，σ2），其中μ近似为样本平均数，σ2近似为样本方差s2.

（ⅰ）利用该正态分布，求P（187.8

（ⅱ）某用户从该企业购买了100件这种产品，记X表示这100件产品中质量指标值位于区间（187.8，212.2）的产品件数，利用（ⅰ）的结果，求EX.

附：150[KF）]≈12.2.

若Z～N（μ，σ2）则P（μ-σ

解答 （Ⅰ）抽取产品的质量指标值的样本平均数和样本方差s2分别为：

=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200，

s2=（-30）2×0.02+（-20）2×0.09+（-10）2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.

（Ⅱ）（ⅰ）由（Ⅰ）知Z～N（200，150），从而P（187.8

=0.6826；

（ⅱ）由（ⅰ）知一件产品的质量指标值位于区间（187.8，212.2）的概率为0.6826，

依题意知X～B（100，0.6826），所以EX=100×0.6826=68.26.

本题主要考查频率分布直方图的统计原理，离散型随机变量的期望和方差，以及正态分

布的特点及概率求解，考查运算求解能力，第1小题较为常规，考查样本平均数与样本方差

的基本统计知识，第2步让笔者眼前一亮，给出“3σ原则”数据，巧妙地考查了正态分布的μ

和σ，既减轻了学生背3σ原则的繁琐性，又考查了学生的数据处理能力，重视应用，避开

难题怪题，对学生能力的考查很是深刻，一味的背诵、大量的题海战术、传统的填鸭式教学已经跟不上高考改革.

2015年试题：某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到散点图（图4）及一些统计量的值.图4

∑8i=1（xi-）2∑8i=1（wi-）2∑8i=1（xi-）（yi-）∑8i=1（wi-）（yi-）

46.65636.8289.81.61469108.8

表中wi=xi，=18∑8i=1wi.

（1）根据散点图判断，y=a+bx与y=c+dx哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）

（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；

（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据（Ⅱ）的结果回答下列问题：

（ⅰ）年宣传费x=49时，年销售量及年利润的预报值是多少？

（ⅱ）年宣传费x为何值时，年利润的预报值最大？

附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为：[AKβ^]=∑ni=1（ui-）（vi-）∑ni=1（ui-）2，[AKα^]=[AKv-D]-[AKβ^][AKu-D].

解析 （1）y=c+dx适宜，由图像分析可知符合抛物线的方程.

（2）d=∑8i=1（wi-）（yi-）∑8i=1（wi-）2=108.81.6=68，

=-d=563-68×6.8=100.6，

所以y=68x+100.6.

（3）z=0.2y-x=13.6x+20.12-x=-x+13.6x+20.12，由x=49可得z=-49+13.6×7+20.12=66.32，z=-（x）2+13.6x+20.12，当x=6.8可得x=46.24时，年利润的预报值最大

本道题考查散点图，回归方程，试题新颖，不偏不怪，给出关键数据，需要学生能从大量数据中抽取对研究问题有用的信息，并作出判断，会整理分析并解决问题，对学生数据处理能力要求较高，有很好的考查功能.

3 试题选拔功能的加强

高考试题是为高等学校招生服务的，它的功能就是选拔，近几年的全国1卷的第21题均考查函数与导数，对学生的推理论证能力、运算求解能力要求很高，有很高的信度、效度和区分度，现以2015年全国1卷第21题为例作说明.

2015年试题：已知函数f（x）=x3+ax+14，g（x）=-lnx

（Ⅰ）当a为何值时，x轴为曲线y=f（x）的切线；

（Ⅱ）用min{m，n}表示m，n中的最小值，设函数h（x）=min{f（x），g（x）}（x>0），讨论h（x）零点的个数

解析：

（Ⅰ）根据已知，f′（x）=3x2+a，若x轴为曲线的切线，设切点横坐标为t，则可得

f′（t）=0，

f（t）=0，即3t2+a=0，

t3+at+14=0，解得a=-34，

t=12.

所以当a=-34时，x轴为曲线y=f（x）的切线.

（Ⅱ）当a≥0时，f′（x）=3x2+a>0，于是f（x）单调递增，而f（0）=14，于是y=f（x）与y=g（x）

有唯一交点，且交点的横坐标P∈（0，1），此时函数h（x）的零点个数为1.

当-340，

此时y=f（x）与y=g（x）在（0，1）内有唯一交点，函数h（x）的零点个数为1.

当a=-34时，此时极小值为0，函数h（x）的零点个数为2；

当-54

当a=-54时，此时y=f（x）与y=g（x）相交于（1，0），函数h（x）的零点个数为2；

当a<-54时，此时y=f（x）与y=g（x）的交点的横坐标大于1，此时函数h（x）的零点个数为1.

综上可得，函数h（x）的零点个数为：

1，a<-54或a>-34，

2，a=-54或a=-34，

3，-54

本试题很朴素又很大气，学生很熟悉却又很难答满分，会做但不太容易做全对，试题考查的区分度跃然纸上，第一题较为简单，考查曲线与直线相切有关内容，第二步考查零点的个数，对学生数形结合思想，分类讨论思想，转化与化归思想要求较高，试题平淡无奇，却凸显能力，展示学生智慧，深层次考查学生综合解题能力，其高考选拔功能不言而喻.

紧扣课本，命制试题；少些华丽，多些本质；来点升华，体现选拔；我想这正是命制者的本意吧.