美国高中数学教材知识设置研究

美国没有全国统一的中小学强制数学课程标准，虽然前面有2000年美国数学教师协会制定的数学课程标准，后面有2010年美国全国州长协会（NGA）联合全美首席学校官员理事会（CCSSO）制定了美国中小学数学课程标准《Common Core State Standards for Mathematics》（共同州核心数学课程标准），但是对各州没有强制约束力，各州原来都有自己的中小学数学课程标准，现在有40多个州先后参照《共同州核心数学课程标准》制定适合本州特点的州数学课程标准.各州的新课程标准在参照共同核心课程标准（CCSS）基础上结合本州原课程标准及学生实际制定，随之而来的是各州数学教材的变化，新、旧数学教材还在过度过程中，美国各州旧数学教材由教材出版商依据各州课程标准编写出版，质量和内容层次不齐，高中课程设置因不同州或不同的学区甚至不同的学校而异，每门课程都分四个等级：学术课程（Academics course）， 荣誉课程（Honors course） ， 预备先修课程（Advanced placement ，Pre-AP）、 先修课程（Advanced placement ，简称AP）难度依次增加，主要有代数1，代数2，几何、三角函数，预备微积分等， AP课程要学习大学里的微积分，考试通过了可以折抵大学学分. 本文所研究的教材只指美国采用该教材的州学生用教科书，不包括其他教学材料，通过对AMSCO学术出版公司（AMSCO SCHOOL PUBLISHER）出版的由 Ann、 Xavier 、Gantert等人编写的供美国各州高中学生使用的代数（一）、几何、代数（二）与三角的数学内容加以列举并分析知识点顺序、知识结构编写特点，管窥美国高中数学主要学习内容及知识模块之间结构关系.美国高中根据学生的不同数学基础开设各类相关数学课程供学生选修，例如还有预科代数”（pre-Algebra）、高阶数学概念（Advanced maths concept）等.限于篇幅，本文只研究美国部分高中采用的三门课程所用教材.

1 AMSCO高中数学教材及课程标准学习内容

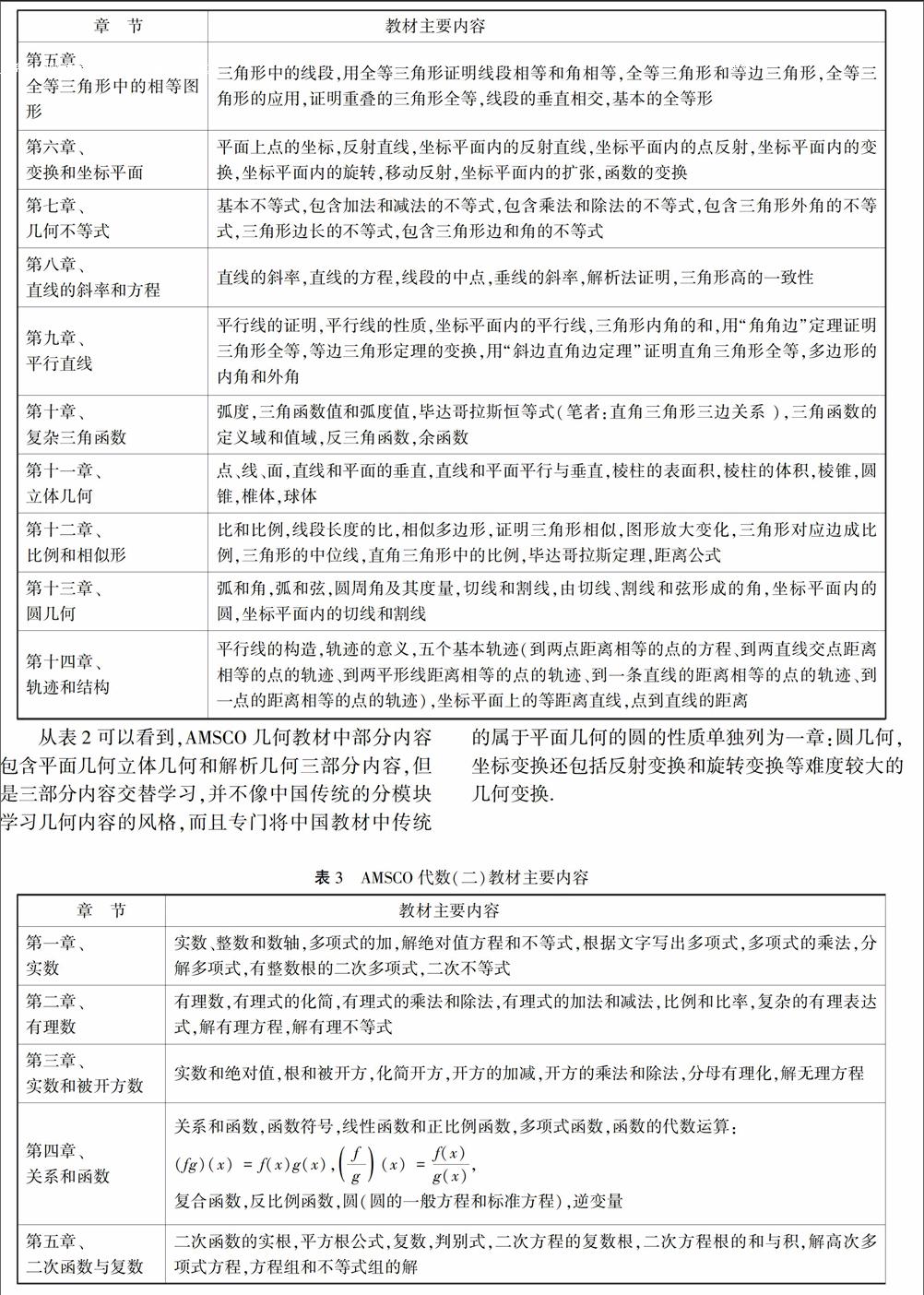
下表1、表2、表3分别列出美国AMSCO学术出版公司高中代数（一）、几何、代数（二）教材内容.

AMSCO代数（二）中三角函数的学习较为系统和完整：三角函数的图像和性质、三角恒等式、三角方程、三角函数应用等，表3中函数的代数变换主要讲函数的复合变换性质：（f+g）（x）=f（x）+g（x）， （f-g）（x）=f（x）-g（x），（fg）（x）=f（x）g（x），（f/g）（x）=f（x）/g（x）等性质及其应用.

2 AMSCO教材整体知识结构比较分析

2.1 AMSCO数学教材内容相对比较简单

从表1可以看出，美国高中教材中很多内容比中国大陆现行教材中的内容简单很多，例如：代数（一）中分式的近似值、有效数字、小数点后小数保留位数、无理数、乘法和除法、代数式的加减、解一次方程和一次不等式等，几何中的直线、线段、角和三角形全等等内容，上述内容都是中国新课程教材中初中就需要学习的内容，还有比例和比率这样的内容在中国都属于小学和初中的必修内容.

2.2 AMSCO教材的代数、几何和概率之间总体上体现出各模块分割编写

从表1、表2、表3 内容可以看到，代数（一）和代数（二）的内容总体上按照数与代数→函数→三角→概率统计这样的顺序编排知识点，几何部分按照几何概念→平面几何→解析几何→立体几何这样的顺序编排，也有少量的不同模块知识混合编写的情况，例如代数（一）教材中也有几何内容出现：几何图形、面积和体积、直角三角形等，而几何教材中有三角运算内容.

2.3 超越方程仍然是美国高中代数教材的重点内容

从美国代数（二）教材内容看，中国上世纪80—90年代使用的全国通用高中数学教材中的指数方程、对数方程、三角函数、三角方程等内容仍然是美国高中教材中的主要内容，上述内容是在学习指数函数、对数函数、三角函数及简单代数方程基础上的升华内容，也是对线性方程等简单代数知识的拓广和加深.

2.4 三角函数的知识脉络结构和中国大陆旧教材风格相似

美国教材中对三角函数的学习也通过比例→直角三角形中的三角比→一般三角形中的三角函数→广泛意义上的角的三角函数这样的顺序来学习，这种风格和中国上世纪80—90年代使用的全国通用高中数学教材中三角函数的知识脉络安排相似，这种风格从形象到抽象、从数到代数形式，逐渐过渡，应该是符合学生心理发展规律的，而且，美国教材沿袭西欧传统风格，这种知识结构安排方式应该是久经实验、比较有效的范式.

2.5 欧式几何知识的学习仍然是美国高中数学学习的主要内容

从上述表1、表2、表3内容看，欧式几何的基本内容仍然是美国高中学生数学学习的重要组成部分，并且基本上还是按照《几何原本》的公理体系结构模式来安排知识顺序，先是几个公设作为基础，在公设基础上推理出定理和性质，《几何原本》的公里体系模式以及严格的推理证明方法是训练逻辑思维的基本而有效的方法.虽然对欧式几何的争议一直未断，但是现在看来欧几里得并没有从西方数学教材中“滚蛋”.

2.6 知识呈现方式细腻而精致

AMSCO教材中数学知识的呈现详细而细腻，例题先分析再解题，步骤完整而精致，整本书知识呈现“如烹小鲜”，娓娓道来，步步为营，节奏有序而平稳，练习题按照难度分层设计：PART Ⅰ、PARTⅡ、PART Ⅲ；几何内容的学习也是预先学习证明方法：归纳推理，充要条件（difinition as biconditionals），演绎推理，直接和间接证明，假设、定理和证明，条件（笔者：或题设）的加和减，等量代换、等量乘等量，等量除等量，等量的平方和开方，再学习具体几何知识的证明：平面几何、解析几何、立体几何.

3 结论与启示

3.1 按照数学知识分模块编写教材仍然在美国被采用值得思考

全球各国数学教育界一度曾热议可否打破数学知识模块之间的籓篱，让不同的数学分支内容之间相互融合、相互渗透、相互支撑，还原数学发展过程中的本来面目，包括中国大陆在内的各国数学教材也做了很多尝试，但是数学本身的发展过程漫长而零碎，缺乏系统性，要让学生在短短3、4年内完成较多的数学内容的学习，分模块学习也许是必要的，传统知识编排模式在英国和俄罗斯教材中仍然保持，当然，打破不同数学分支之间的籓篱，能融会贯通地学习数学，能让学生体会到数学的本来面目，有利于学生今后对数学的学习和应用以及自身的发展，但是需要编写教材的人有很扎实的数学功底和开阔的数学视野，同时也要具备教育学、心理学知识，才能编写出学习效率较高的教材来.

3.2 精致而细腻的知识呈现模式适合基础薄弱的学生学习

中国大陆上世纪80—90年代的高中教材全国通用，一纲二本，考虑到不同地区学生的基础差异，编写了两种版本的教材供学生选用：甲种本和乙种本，均由人民教育出版社编写出版，依据当时的数学教学大纲编写，乙种本稍微简单，但是知识呈现更加细致，细节性知识减少，笔者经历了这两种版本教材在不同学校使用的效果，很多采用乙种本的学校，学生学习成绩反而优于采用甲种本的学校，AMSCO教材的知识呈现模式细致而繁杂，表2的几何内容就洋洋洒洒600多页，对成绩优秀的学生看来可能没有必要，但是对于数学底子薄弱的学生来讲却非常有必要，所有概念都罗列出来，例题解题过程完整而仔细，有利于学生对知识的归纳，也有利于学生学习到规范的解题方法和思维模式.

参考文献

[1]王奋平，喻平.英国高中数学教材只是整体结构设计研究〔J〕.数学教育学报，2013（5）：32-36.

[2]王奋平.中、英高中数学教材复数内容比较研究 〔J〕.数学教育学报，2011（6）：51-55.

[3]王奋平.中、英高中数学教材比较研究 〔J〕.数学教育学报，2011（4） ：83-86.

[4]王奋平，孔凡哲.中、英高中数学教材比较研究〔J〕.中学数学教学参考，2012（7）：35-37.

[5]王奋平.英国两种高中数学教材比较研究 〔J〕.数学教育学报，2013（4）：76-80.

[6] Ann，Xavier ，et. ALGEBRA1， ALGEBRA2 AND TRIGONOMETRY， Geometry

〔M〕. AMSCO SCHOOL PUBLISHER （1998）

[7]http：//highschool.shs.k12.ny.us/IntegratedAlegbra2