空气中的声速测量

袁淑立　于桂凤　潘维

【摘 要】空气中的声速测量是个综合性很强的物理实验，在实际应用中也具有非常重要的意义，因此许多高等院校都把它列为必选的基础实验。本文用共振干涉法和相位比较法对空气中的声速进行了研究，得到声波在空气中的传播速度分别为341.54 以及 341.99m s-1，与理论值343.54 m s-1比较接近，最后对实验数据进行了误差处理。

【关键词】声速；空气；共振干涉法；相位比较法

0 引言

近几年来随着声学的发展，检测声学在现实生活中得到了越来越广泛的应用。比如：无损检测、流体测速、探伤、定位、测距等[1]。声速的测量在声学检测领域占有非常重要的地位。空气中的声速测量实验因其应用性强、便于操作、易于实现等优点被很多高校选作基础物理实验。媒质的特性及状态等因素决定了声波在其中传播的速度，通过媒质中声速的测定，如：测量氯丁橡胶乳液的比重、氯气、蔗糖的浓度以及输油管中不同油品的分界面等等可以了解媒质的特性或状态变化，因此声速测定在某些工业生产上具有非常重要的实用意义[2]。在教学中一般采用以下两种理论方法来测量声速：第一种是测量声波传播的距离s和时间t，然后根据公式v=s/t计算出声速。这种方法中学采用的比较多。另一种是测量声波的频率f和波长λ。然后根据任何相邻的振幅最大值的位置之间波动过程中波速v、波长λ和频率f之间存在着下列关系：v=λf，计算出声速[3]。目前高校中普遍采用的是这套理论。而在实际操作中，也有很多不同的方法来实现。例如双踪示波法[4]，声音共鸣法[5]，驻波法[6]等。本文中本文用共振干涉法和相位比较法首先测定了声速在空气中的传播速度，并与理论值进行比较，然后进行误差分析，以便检测测量方法的实用性。

1 理论方法

1.1 共振干涉法（驻波法）

声源S1发出的声波经空气传播到位置S2，S2在接收S1的声波信号的同时反射部分声波信号，如果接收面与发射面严格平行，则入射波就在接收面上垂直反射，反射波与发射波会产生相干涉就会形成驻波。声源S1发出声波的振动方程为：A1=Acos（wt-2πx/λ），声源S2反射的声波的振动方程为A2=Acos（wt-2πx/λ），两者相互叠加形成的驻波的振动方程为：A3=2Acos（2πx/λ）cos（wt），w为声波的角频率，t为声波传播经过的时间，λ为测量声波的波长，x为声波经过的距离。可以看出两列波叠加之后形成的驻波的强度随距离之间按cos（2πx/λ）规律变化。如果改变S2位置，即改变S1与S2之间的距离，则任何相邻的振幅最大值的位置之间或者相邻的振幅最小值的位置之间的距离均为λ/2。

1.2 相位比较法

声源S1发出声波后就会在其周围形成声场，设声源S1的振动方程为A1=Acos（wt），但是在声场中的任一点S2的自振动相位是随时间而变化的，例如S2接收到的振动为A1=Acos（w（t- x/v）），但此点和声源的振动相位差不随时间变化。S1 和S2振动的相位差为？驻φ=ωx/v。当x=nλ，合振动为一斜率为正的直线，当x=（2n+1）λ/2时，合振动为一斜率为负的直线，当x为其它值时，合成振动为形状不同的椭圆形，移动S2，当其合振动连续两次为正斜率直线时，S2移动的距离即为一个波长。

2 数据处理

2.1 声波频率的测定

任何相邻的振幅最大值的位置之间波动过程中波速、波长和频率之间存在着下列关系：v=λf，观察接收波的电压幅度变化，在某一频率点处电压幅度最大，此频率即是f。改变S2的位置（即改变S1、S2之间的距离）直至示波器显示的正弦波振幅达到最大值，再次记下此时频率f的数据于表1。

2.2 共振干涉法测量声波的波长

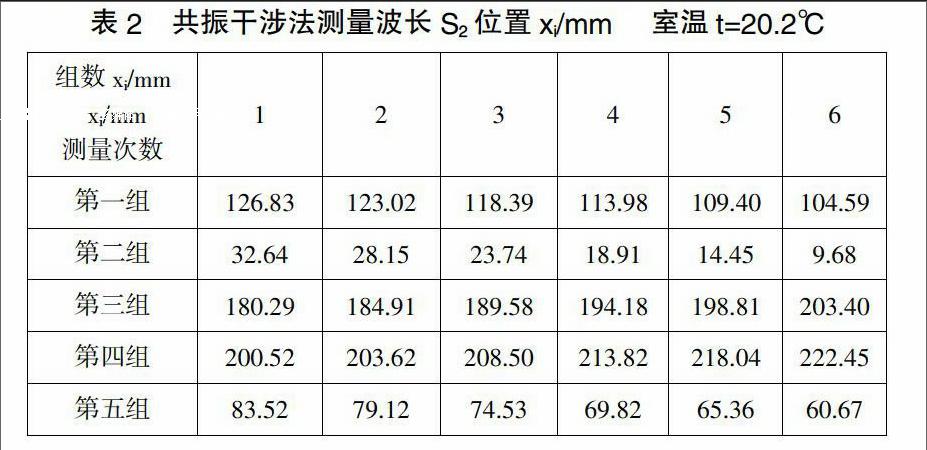
改变S1、S2之间的距离，当接收波形的振幅为最大值时，读出S2的位置x1，沿同一方向继续改变S1、S2之间的距离，当波形振幅再次为最大时，读出S2的位置x2， 为了提高测量的准确性，共测量五组数据，每组测量6次，把每次测量的数据列xi，记录到表格2中。

2.4 相位法测量声波的波长

对于相位法来说，首先观察李萨如图的变化规律。当观察到波形为正斜率直线时，记下S2的位置x1，改变S2 的位置，记下示波器出现正斜率直线时S2的位置x2。为减少误差，S2 的测量位置改变了6次。然后重新改变S2的起始位置，重复刚才的步骤，一共测量五组数据。把每一组测量得到测量列 xi记入表格3中。

2.6 结果分析

在测量时，误差虽然无法消除，但我们可以通过多种方法减少误差。第一种是多次重复测量取平均值。在一组条件完全相同的重复实验中，个别测量值肯能会出现异常，如测量值偏大或偏小，多次重复测量可以使测量值分布更平均，测量结果更接近真值。在这个试验中，每次实验都重复测量5组数据。例如驻波法测量声波的波长中，虽然单次测量存在一定的误差，声波的波长结果分别是346.69m/s，344.08m/s，337.75m/s，342.59m/s，在这些结果中有的大于理论值，有的小于理论值，但是取平均值后就比较接近于理论值，多次重复测量的方法可以减少误差的产生，提高测量的准确度。第二种是利用逐差法处理数据。所谓逐差法，是把测量数据中的因变量进行逐项相减或按顺序分为两组进行对应项相减，然后将所得差值作为因变量的多次测量值进行数据处理的方法。逐差法可以提高实验数据的利用率，减小随机误差的影响，是物理实验中处理数据常用的一种方法。

逐差法是针对自变量等量变化，因变量也做等量变化时，所测得有序数据等间隔相减后取其逐差平均值得到的结果。其优点是充分利用了测量数据，具有对数据取平均的效果，可及时发现差错或数据的分布规律，及时纠正或及时总结数据规律。这里在计算声波波长时我们用逐差法处理数据保持了多次测量的优点，充分的利用了所有的测量结果，尽可能的减小了误差，提高了测量的准确性。

3 结论

首先由声速测定专用信号源读出声波频率，用共振干涉法和相位比较法求出波长。最后由v=λf分别得到声波在空气中的传播速度，实验值与理论值比较接近，说明这两种方法测量声速的可行性。

【参考文献】

[1]张涛，黄立波，等.空气中声速测量的实验研究[J].西安科技大学学报，2004，24（4）：518-521.

[2]姜永超.空气、液体介质中的声速测量[M].大学物理实验，北京：中国农业出版社，2015：154-151.

[3]朱鹤年.物理实验研究[M].北京：清华大学出版社，1994：219-233.

[4]魏国瑞，潘沛，等.超声波声速测量新方法[J].西安建筑科技大学学报，2009， 36（3）：75-78.

[5]操良平.用“声音共鸣”法测空气中的声速[J].物理教学探讨，2007，25（287）：59-60.

[6]郑庆华，童悦.声速测量实验的理论分析[J].宜春学院学报，2006，28（4）：44-46.

[责任编辑：杨玉洁]