方格网法、断面法、DTM 法土石方量计算选择应用

■陈 斌，祝 涛

■1.核工业西南勘察设计研究院有限公司，四川 成都 610052;2.四川省地质测绘院，四川 成都 610017

1 引言

不同的土方计算模型，由于其外业测量方法的差异以及土方计算原理的不同，其土石方计算量往往存在差异。所以，根据不同的地形地貌特征选择适宜的土方计算方法，计算参数，对尽可能准确的计算土石方量具有现实意义。下面分别以一个地形起伏较小的区域(某中心湖在开挖前的原始地形)和另一个地形起伏较大的区域(测区海拔高度达到两千多米的茂县某地块)土方平衡为例，分析方格网法、断面法、DTM法等典型土石方计算方法的适宜性。

2 方格网法

展绘好高程点后，在南方CASS 软件下，计算出所选区域土石方量的大小。根据分析可知，某中心湖是属于起伏较小的地形情况，如图1，其最大高程与最小高程值之差为2.585 米。茂县某地块最大高程与最小高程的差距达到了88.242 米，属地形起伏相对较大的区域，如图2。设计高程(或目标高程)的获取可通过区域土方平衡的方式获取，见图1、图2。

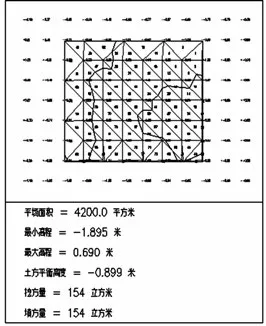
图1 某中心湖区域土方平衡

根据误差理论，以各个格网宽度的倒数值作为对应方格土方量的权值，最后通过取加权平均值，可以得到不同地形情况下土方量的最或然似值V。设各个填挖放量值为Vi，则最后可以利用V 值求得中误差m。计算公式如下:

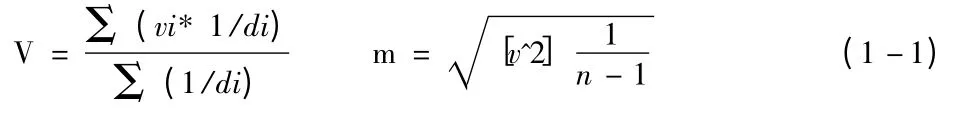
di 格网宽度值;

n 最或然值计算次数。

图2 茂县某地块区域土方平衡

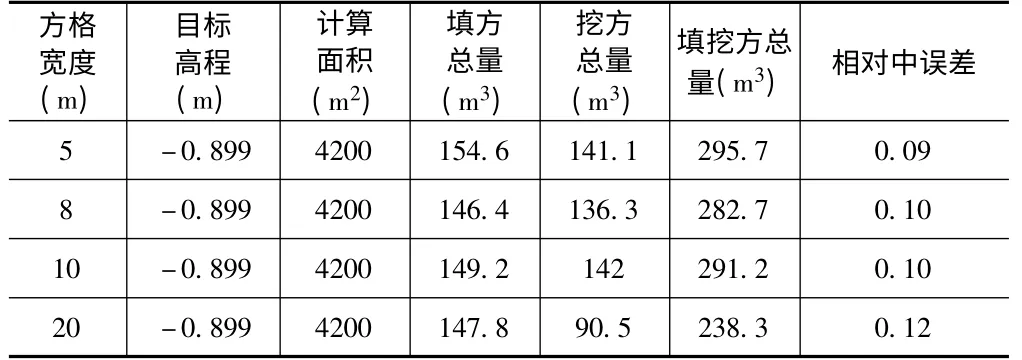
表1 某中心湖(地形比较平缓)在方格网法下土石方计算

经计算得:V1=285.3(方)m1=28.04(方)

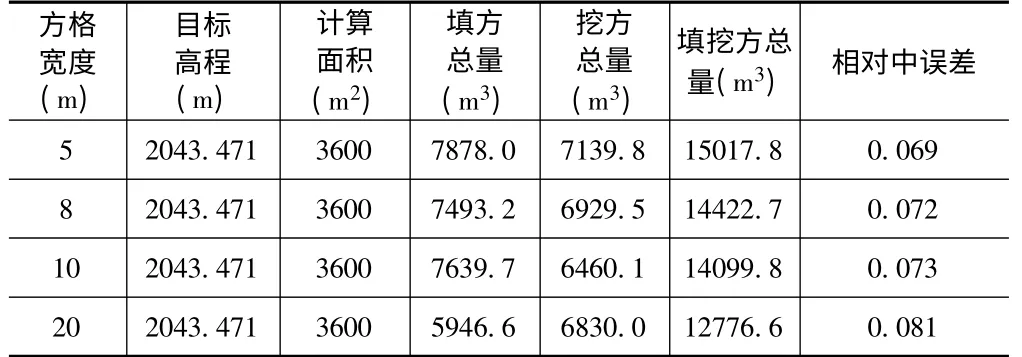
表2 四川茂县某地块在方格网法下土石方计算

经计算得:V2=14432.02(方)m2=±1031.82(方)

通过计算分析可知:

(1)随着方格宽度的增加，其结果计算出来的相对中误差也有增加的趋势，所以在条件应允时方格网的格网宽度值的设定对土石方量的准确计算有重要影响。

(2)方格网法相对于起伏较小的地形来说不适合于计算起伏较大的地形的土方量。

3 断面法

在CASS 软件中利用场地断面法计算指定区域的土石方量。计算结果如表3、表4、表5、表6。

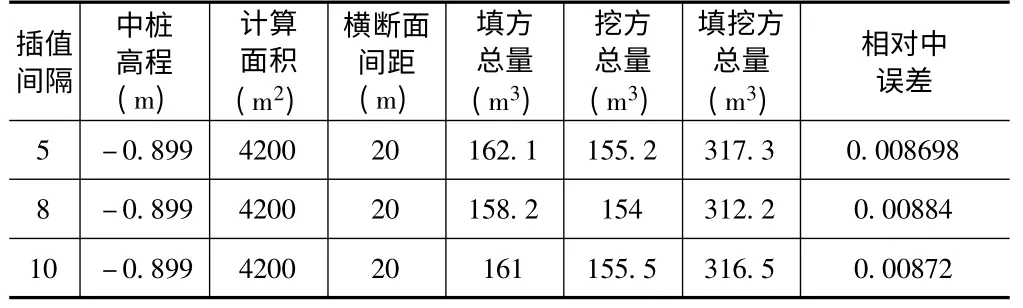
表3 某中心湖断面法计算示例(横断面间距20 米)

经计算得:V3=315.6(方)m3=±2.76(方)

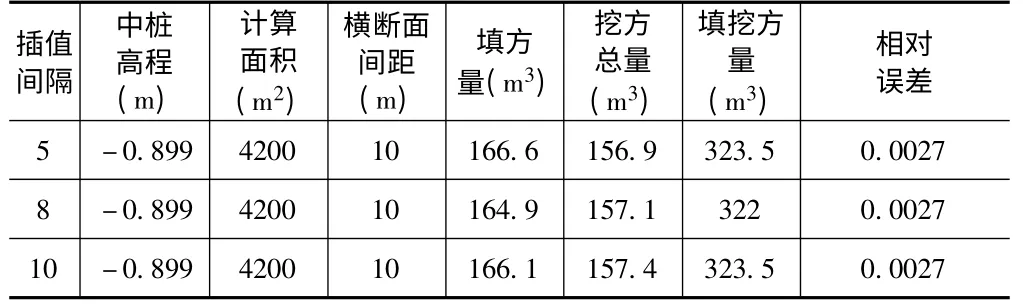
表4 某中心湖断面法计算示例(横断面间距10 米)

经计算得:V4=323(方)m4=±0.87(方)

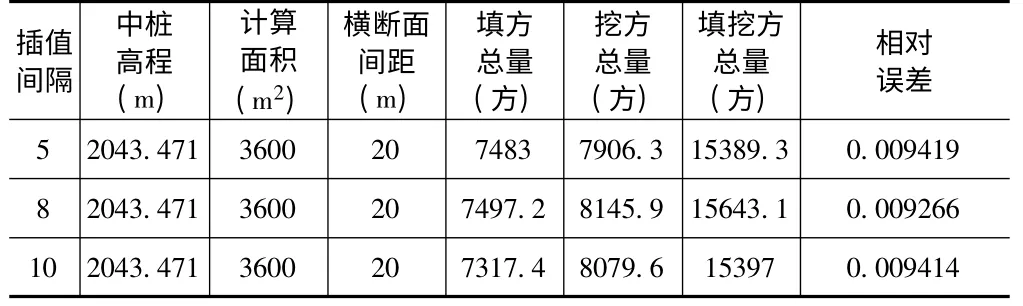
表5 茂县某地块断面法计算土方示例(横断面间距20 米)

经计算得:V5=15465.76(方)m5=±144.95(方)

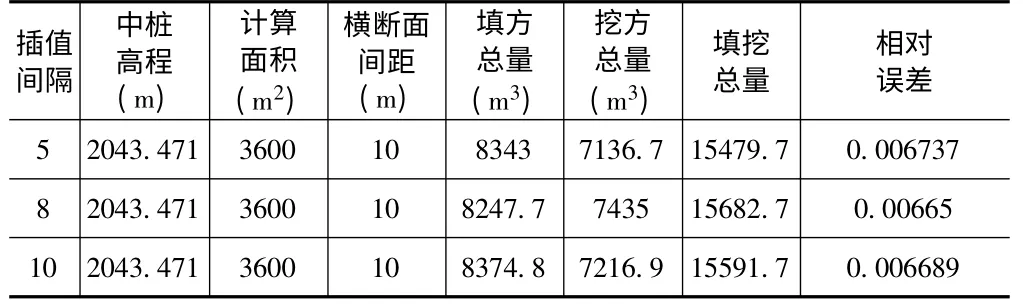
表6 茂县某地块断面法计算土方示例(横断面间距10 米)

经计算得:V6=15565.76(方)m6=±104.29(方)

通过对四组数据表的不同组合对比可以得出。

(1)由表3、表4 以及表5、表6 分别对比，在条件相同的情况下为了提高用断面法计算土石方量的精度可以减小横断面之间的间距。

(2)由不同的地貌特征下可以得出在相同的横断面间距的情况下，断面法相对于地形起伏较大的区域更适宜于地形起伏较小的区域的土石方量的计算。

(3)对于相同的区域，横断面间距较小的数据组所计算得到的土方量的相对中误差较小。

4 三角网(DTM)法

在CASS 软件中利用根据图上高程点来计算指定区域的土石方量。计算结果参见表7、表8。

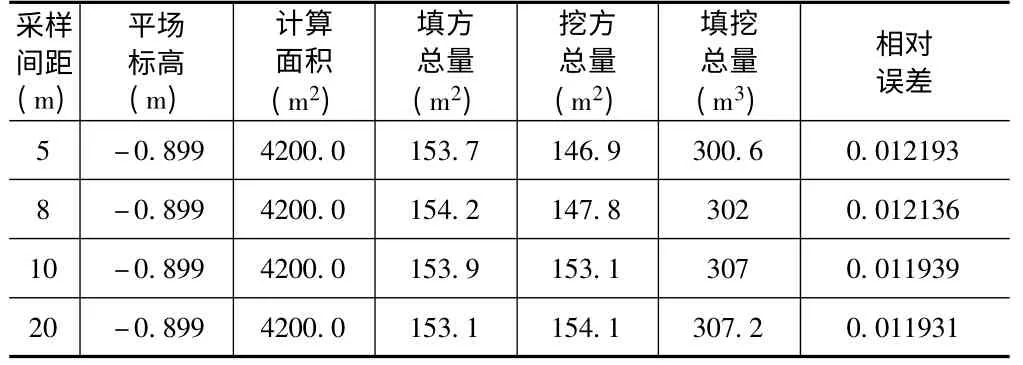
表7 某中心湖DTM 法土方计算

经计算得:V7=303(方)m7=±2.665(方)

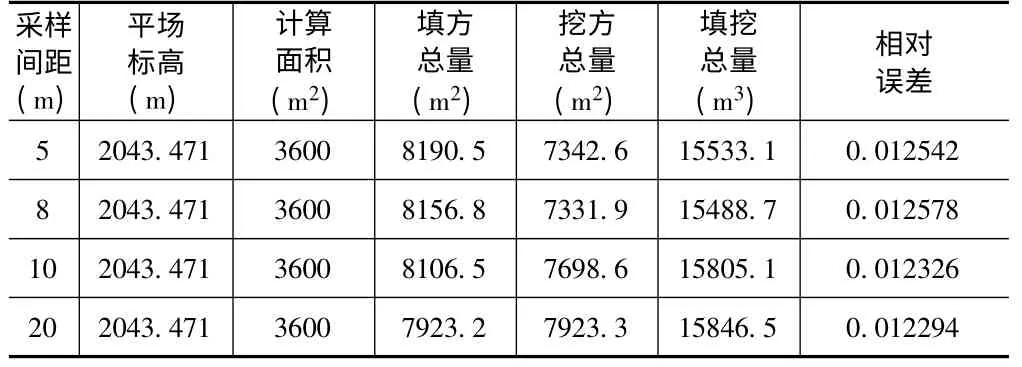
表8 茂县某地块DTM 土方计算

经计算得:V8=15511.7(方)m8=±134.8(方)

根据以上两表计算结果的对比分析可知:

(1)从中误差角度来看，DTM 法计算土石方量是同样更加适合于地形平坦、起伏较小的区域。

(2)但是从相对中误差来比较分析DTM 法在这两种地形情况下计算出来的土方量差距较小。所以这样子考虑的话，可以认为DTM 法在计算土方量的时候是没有地形条件限制的。

(3)在以上指定区域中，利用DTM 法计算土石方量其采样间距对计算结果的影响比较小。

5 不同方法计算结果与分析

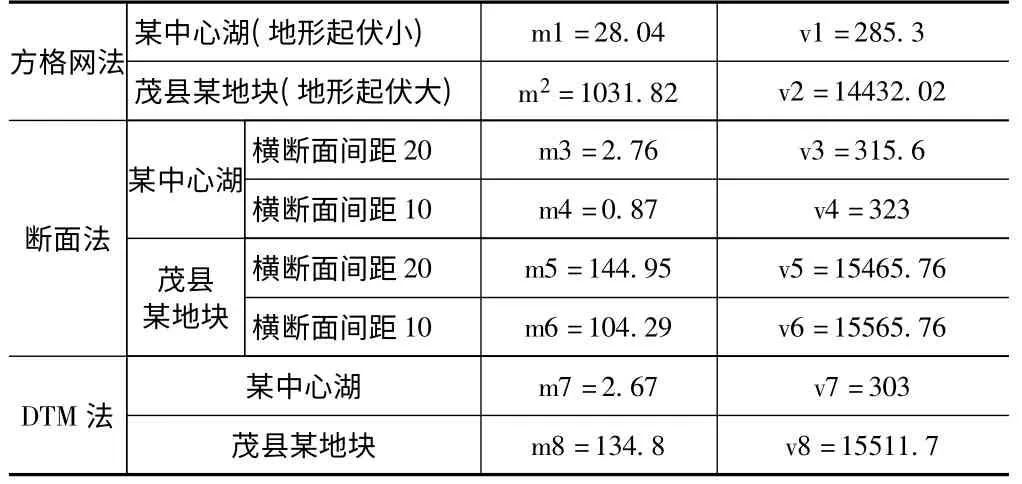
表9 三种计算方法综合

通过对以上结果的分析可以得出:

(1)当方格网法在计算地形起伏很大的区域的土石方量的时候，其中误差较大，如表2 所示。但是在具体的实际工程中到底利用什么方法进行计算还应该参考相对中误差来判断。

(2)从表1 到表8 相比较容易发现，在如表所示地形地貌情况下，断面法和DTM 发所计算出来的精度都高于其所对应的方格网法。根据表9 所示断面法和DTM 法计算出来的结果相差不大，所以不能够得出DTM 法优于其他的土方计算方法，这还同在分别利用这些方法计算时的各自的参数的设置相关。

6 结束语

通过以上分析可知，实际过程中不能够绝对的得出那一种土方计算方法就一定比另外的土方计算方法优越。应根据不同地貌特征，结合各自的特征，综合以上计算模型，予以选择计算参数，选择计算方法。