海南市县过夜游客人数与饭店行业特征关系研究※——基于17个市县面板的计量分析

袁奥博 徐 艳

(1.西南财经大学金融学院，四川 成都 611130;2.海南大学经济与管理学院，海南 海口 570228)

海南省旅游资源丰富，旅游业在海南国民经济中占据重要的地位，是海南省主要支柱产业之一。2010年海南国际旅游岛建设上升为国家战略，海南省经济、社会、文化和生态建设都取得了长足的进步，旅游业的发展更为繁荣。旅游业的可持续性发展对其他领域的可持续发展具有一定的促进作用，而整个社会的可持续发展又为旅游业创造了良好的条件。其中，旅游业对餐饮、住宿的助推作用越来越明显。饭店行业在满足商务会展、旅游休闲等消费需求的同时，已成为一个地区或城市经济社会发展水平、经贸活跃程度和对外总体形象的重要标志。近年来海南省旅游饭店业规模迅速扩大，整体素质不断提升，市场影响力持续增强，构成了海南省旅游竞争力重要方面，为促进海南服务业繁荣发展和旅游服务水平整体提升做出了积极贡献。旅游业的发展离不开饭店行业的发展和支持，饭店业给游客提供休息和服务，并留下良好印象，优质的饭店服务有助于提升海南国际旅游岛的形象。

对同在海南国际旅游岛的各个市县来说，相互之间也存在竞争，如各地通过深度开发具有本地特色的旅游产品来吸引游客。本文要研究的是海南省各市县过夜游客人数与当地饭店行业特征的关系，因为各地除了开发特色旅游产品和提升旅游服务水平吸引游客以外，还能通过建设高水平的饭店来吸引游客。一个地方游客过夜人数的增加，除了给饭店业带来更多收入以外，还意味着当地潜在的其他旅游相关行业收入的增加，如游客在当地过夜后有在当地的交通需求，也可能同时对当地旅游产品和当地特产产生兴趣，进而形成旅游消费行为，对当地收入产生正向影响。

本研究的意义在于，由于不同地区的饭店业有着不同的发展水平，进而不同地区的饭店特征不同，研究饭店特征是否是吸引游客在当地过夜的因素，首先有助于解释不同地区旅游人数和旅游收入的变化;同时，找出那些显著影响过夜游客人数的饭店特征，有助于各地根据相应的结论对当地的饭店行业进行改善，提升当地旅游业的竞争力，从而提升整个海南岛的旅游服务能力和竞争力;最后，当前关于饭店行业与旅游业之间关系的相关研究是缺乏的，本文的研究可以为填补部分研究空白做出一定贡献。

1 变量定义与数据选取

本研究主要考虑的解释变量为饭店行业特征，包括各市县饭店总数、客房总数、床位数、整体饭店服务水平和发展规模水平，被解释变量则是过夜游客人数，各个特征和变量相应地定义为当地饭店总数(家)、客房总数(间)、床位总数(张)、星级饭店占饭店总数的比例、拥有100间客房以上的星级饭店占饭店总数的比例和旅游饭店接待过夜游客总人数。本文认为，饭店数量、客房数量、床位数量、饭店服务水平和饭店规模发展水平等这些饭店特征均是对海南旅游业发展有正向影响的特征因素，这些饭店特征的数据值升高代表着当地饭店行业的容纳能力、发展水平和服务质量等，都将增加海南各市县旅游者的吸引力。

本研究使用的数据是2006—2012年海南省各个市县的面板数据，海南省共19个市县，由于昌江县和三沙市数据空白，故选取共17个市县的数据进行研究，相关数据来源于历年《海南统计年鉴》。对过夜游客人数、饭店数量、客房总数量和床位总数量四个变量取自然对数处理，分别用符号表示为 lntts、lnhs、lnhr和 lnhb，饭店服务水平和饭店发展规模水平两变量不做处理，分别表示为hsl和hdl。最终数据的描述性统计量见表1。

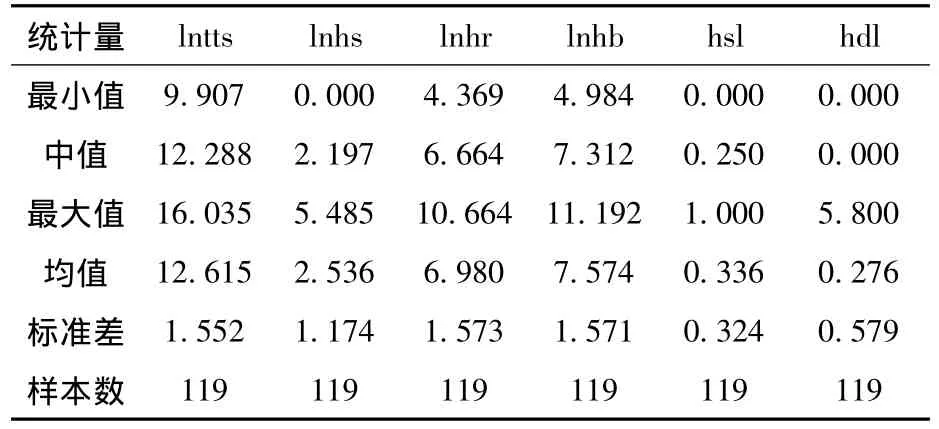
表1 数据描述性统计

2 建模初步

2.1 单位根和协整检验

在计量建模前要考虑避免使用非平稳数据出现伪回归，使用llc、ht、dfuller和 pperron面板单位根检验对面板数据序列进行平稳性检验。为避免篇幅过大，这里不列出单位根检验结果(和Kao协整检验结果)。单位根检验结果表明在1%的置信水平下lntts水平平稳，其他变量一阶平稳，为I(1)单位根过程。根据张晓峒(2001)在多元回归分析中被解释变量的单整阶数不能高于任何一个解释变量的单整阶数，［1］该面板数据单位根过程符合协整前提条件。使用Kao检验对面板进行协整检验，以检测数据之间是否存在长期稳定的关系。协整检验结果表明在1%的置信水平下旅游人数与各饭店特征存在协整关系，其关系是长期稳定的，进行计量回归分析不会出现伪回归。

2.2 普通模型估计

出于对估计结果的谨慎性，为避免单一估计模型造成的统计偏误使得出现有偏的结论，同时使用5种常用的估计模型进行参数估计，分别是混合效应模型(ME)、随机效应模型(RE)、固定效应模型(FE)、极大似然估计法模型(MLE)和面板修正误差模型(PC)，这些普通模型的建立有助于初步了解饭店行业特征与过夜游客人数之间的关系，模型的参数估计见表2。在表2的普通模型参数估计结果中，lnhs和lnhb系数显著为正，意味着饭店数量和床位数的增加将导致游客人数的增加。饭店数量和饭店床位总数虽然都对过夜游客人数有正向影响，但其作用路径机制是不同的，前者是通过自助游游客，后者是通过旅行团游客。由于自助游游客不容易获取各地客房数和床位数的信息，选择在哪个市县的饭店住宿时主要考虑的是当地饭店数量及获得住宿的可能性。参与旅游团的游客则通常服从旅行社安排，相比自助游游客，旅行社对各地区的饭店住宿情况有着相当大的信息优势，旅行社可以根据地区的客房数和床位数是否足够满足旅行团的需求而决定在哪个地区、哪个饭店住宿。

hls和hdl系数为正，但是并不显著非0，意味着饭店行业的服务水平和发展规模对当地过夜游客人数可能无显著影响。一般而言，饭店服务水平高则会吸引游客过来留宿，地区服务水平较好的饭店口碑较好，对游客更有吸引力，但这里不显著，其原因可能是该面板数据本身特质与估计方法不一致导致的。饭店行业的发展规模不显著的原因可能是饭店业的发展规模不能给游客直接感受，不能影响游客对饭店的选择。基于普通模型对饭店服务水平的参数估计结果不显著，其原因可能是该面板数据本身特质与估计方法不一致导致的，所以需要对面板数据进行检验并依据结果进行稳健性估计。

lnhr显著为负，意味着饭店业的客房数的减少反而有助于过夜游客人数的增加，这与旅行社根据各地区客房数来决定选择住宿地区的推论不一致;可能的解释是由于各地饭店客房开房率不高，平均约60%，客房过多而盈利能力不足，减少客房可节约开支并将资金用于提升饭店的服务，从而增加当地的过夜游客人数。从这个角度来看，客房数减少虽然有助于过夜游客人数的增加，但这个变量是外生变量，故将lnhr作为hsl的工具变量，运用两阶段最小二乘法估计得到2SLS模型，估计结果仍见表2，2SLS模型的估计结果表明使用客房数作为饭店服务水平的工具变量，改变了估计方法使得hsl系数相比其他5个普通估计变得显著，这首先说明减少客房能提升服务质量从而增加过夜游客人数的推论是正确的，其次地区饭店行业的服务水平的提高很有可能提升对游客选择在当地住宿的吸引力。

表2 普通模型估计

3 稳健性估计

3.1 模型效应判定

为得到稳健的参数估计，明晰饭店行业服务水平是否对过夜游客人数有显著影响，首先应判定模型面板数据建立何种效应的模型更为合适，以及是否应该包含时间效应。运用拉格朗如乘数法构造LM统计量来区分ME模型和RE模型的优劣，运用hausman检验来区分RE和FE模型的优劣，使用Wald检验来检验时间效应是否显著。从表3的检验结果可知，随机效应优于混合效应模型，随机效应与固定效应模型不存在显著差异，应该选择建立随机效应模型;Wald检验表明该面板模型存在着显著的时间效应;所以应建立含时间效应的随机效应模型。

表3 模型效应检验

3.2 面板特征检验

因为面板数据同时具有截面和时间序列的特征，可能存在异方差、自相关和截面相关的问题，如果不将这些问题考虑进模型中则容易造成统计偏误，得出错误的结论。使用Greene(2000)［2］构造的W统计量来检验模型中是否存在异方差;根据 Bera、Sosa-Escudero 和 Yoon(2001)［3］执行自相 关 检 验;根 据 Pesaran(2004)［4］和 Frees(2004)［5］分别构造 Pesaran检验和 Frees检验来检验截面相关性是否显著。面板特征检验结果(结果表格省略)表明在1%置信水平下面板数据模型存在显著的异方差性、序列自相关性以及截面相关性。

3.3 稳健性估计

根据模型效应的判断和面板模型相关特征的检验，异方差、自相关和截面相关等面板数据特征以及时间效应和随机效应等应该作为建立稳健模型的依据。本文使用5类至少考虑了一种面板数据特征的随机效应估计模型，并加入时间效应来研究海南省各市县饭店行业特征与过夜游客人数的稳健性关系。根据Baltagi和Wu(1999)［6］建立使用的Prais-Winsten转换来消除序列相关的AR模型，其基本思想是用最小二乘法估计其误差遵循一阶自回归过程的回归方程。根据Efron和Tibshirani(1993)［7］使用 Bootstrap法获取稳健型标准误模型，其基本思想在于通过从原始样本中执行多次可重复抽样来计算统计量的标准误，在本文中该模型重复抽样1 000次，种子值为1 000。由于AR模型已构造了包含一阶自回归的模型，故设定二阶自相关和异方差参数，使用广义最小二乘法进行再估计得到GLS模型。根据Liang和 Zeger(1993)［8］构造广义估计方程 GEE模型，其好处在于有助于解决面板数据的截面相关问题。根据 Driscoll和 Kraay(1998)［9］，构造“异方差—序列相关—截面相关”稳健型标准误模型Dri＆Kra，由于Dri＆Kra的随机效应模型无法直接得到，故对RE效应进行FE效应转换，对转化后的数据进行估计，从而得到Dri＆Kra的随机效应模型。稳健性估计结果见表4。

从各稳健性估计结果来看，lnhs和lnhb依旧显著为正，lnhr依旧显著为负，hdl仍然不显著。值得注意的是饭店服务水平hsl在稳健模型的估计中均表现出对过夜旅游人数的显著正向影响，这与表3的2SLS估计结果是一致的，这说明海南省各市县饭店服务水平的提高将有助于吸引游客住宿。最后，稳健性估计的5个模型结果仍然具有一致性。

表4 稳健性估计

4 面板VAR分析

在研究中，将简单多元时间序列的线性模型扩展为非线性模型有助于反映经济关系在不同经济背景下的机制性变换。［10］由于统计数据可得性，无法加长面板时间长度，本面板数据为大N小T短面板，不适合建立多变量的面板向量自回归模型，否则会导致非对称矩阵和标准误无法估计的问题，故用每个饭店特征逐一与过夜游客人数建立脉冲面板VAR。

4.1 脉冲响应函数分析

为建立良好有效的面板VAR模型，首先要判断各个VAR模型的最优滞后阶数，基于AIC、BIC和HQIC统计量最小(结果表格省略)和少数服从多数原则均选择4阶滞后。所有面板VAR模型都重复蒙特卡洛实验1000次，设定种子值为1000。利用各饭店特征与过夜游客人数的面板数据建立面板VAR模型，并得到脉冲响应函数，相应的脉冲响应函数图见图1～图5，图中，中间的实线表示脉冲响应函数的响应路径，上下两条虚线分别表示脉冲响应函数的2倍标准差线，两条虚线中的区间意味着脉冲响应函数在上下2倍标准差内潜在的路径。从脉冲响应函数来看，过夜游客数对饭店数量、饭店客房数和饭店床位数受到外部冲击有着类似的正向响应，均先升上，后趋于收敛，而且上升仅为1期，之后下降并收敛。过夜游客数对饭店服务水平受到外部冲击的响应是负向的，先连续下降2期，后上升并逐渐趋于收敛，这说明饭店的服务质量受到的扰动对游客有着较为持久的影响。过夜游客人数对饭店规模水平受到外部冲击的响应始终是正向的，且响应持续上升到第4期之后方开始收敛。

图1 过夜游客人数对饭店数量的脉冲响应函数

图2 过夜游客人数对客房总数的脉冲响应函数

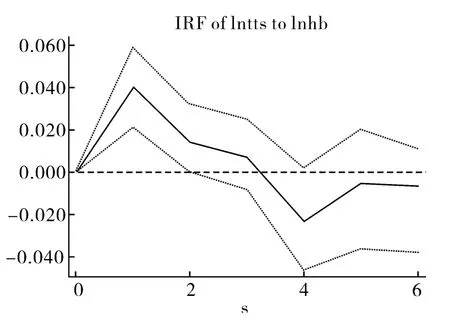
图3 过夜游客人数对床位总数的脉冲响应函数

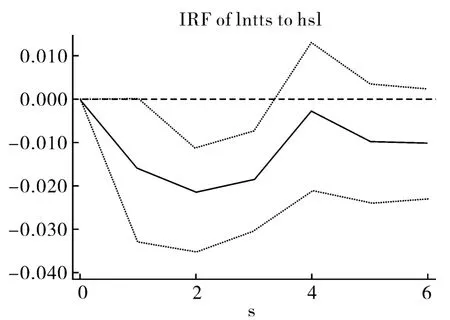
图4 过夜游客人数对饭店服务水平的脉冲响应函数

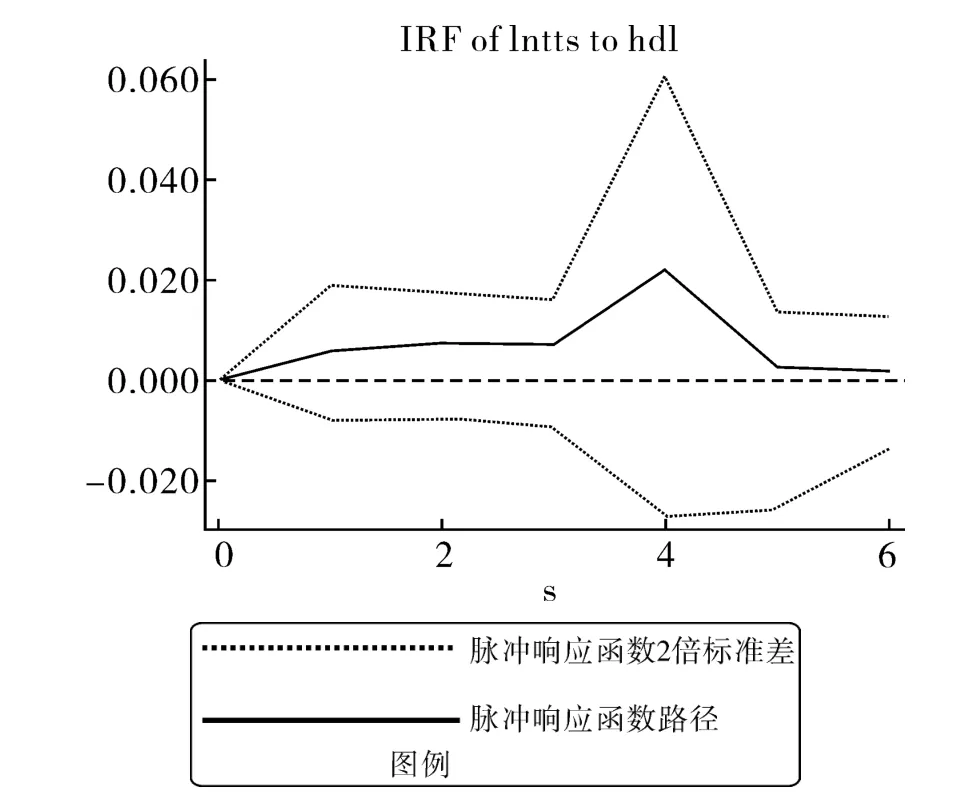
图5 过夜游客人数对饭店发展规模的脉冲响应函数

4.2 格兰杰因果检验

格兰杰因果检验表明的是在控制了被解释变量的过去值以后，解释变量的过去值是否能对被解释变量有显著的解释能力，基于4阶滞后VAR模型的格兰杰检验结果如表5所示。格兰杰因果检验表明，过夜游客人数与饭店数量、饭店客房数量和饭店床位总数有着双向的格兰杰因果关系，而饭店整体服务水平和饭店发展规模水平与过夜游客人数仅存在单向因果关系，即前者是后者的格兰杰原因，而后者不是前者的格兰杰原因。总的来说，海南省的这些饭店行业特征均是过夜游客人数增加的格兰杰原因。

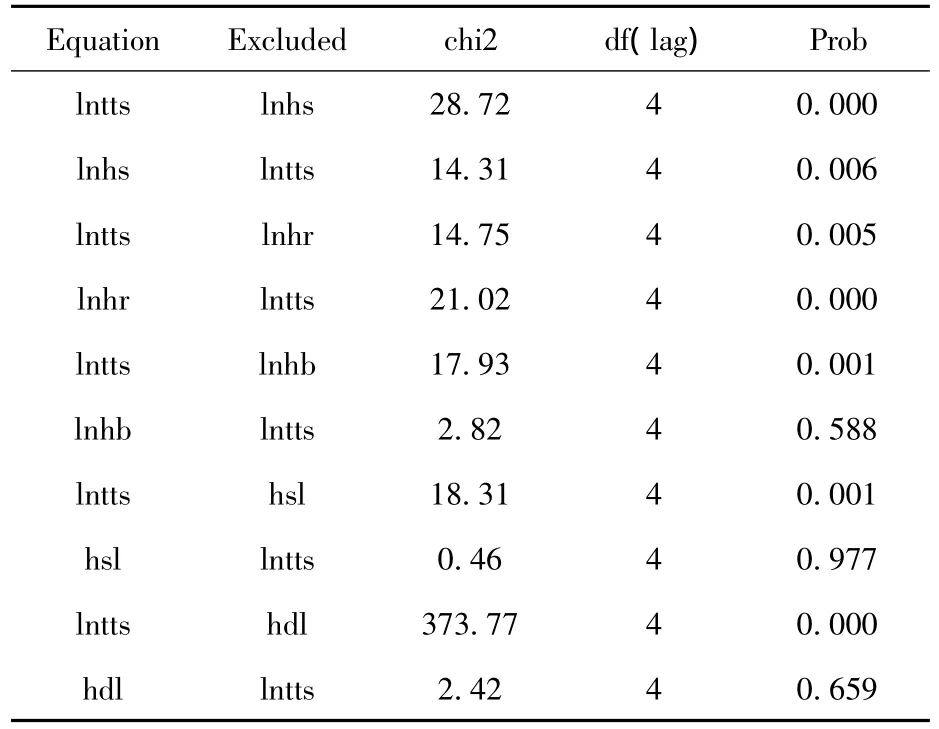
表5 格兰杰因果

4.3 方差分解

在方差分解过程中，由于短面板VAR对变量的容纳能力有限，最大容纳3个解释变量，为避免出现非对称矩阵问题，仅在方差分解中加入3个解释变量。故仅以饭店数表示当地饭店行业的总体容纳能力，并加上饭店业服务水平和发展规模水平，考察三者对各地过夜游客人数的贡献度。根据AIC、BIC和HQIC最小准则选择1阶滞后，由此得到的方差分解见表6。表6表明在饭店特征中，饭店的行业总体容纳能力对过夜游客人数有较大贡献，而饭店服务水平和发展规模水平的贡献则较小，值得注意的是饭店行业的整体服务水平对过夜游客人数的贡献非常小，而且没有任何变化，这说明饭店业应当提高服务水平，增强自身服务对游客的吸引力;过夜游客人数占的比重最大，这说明海南省各市县过夜游客人数变动主要是由其他诸如收入增加、旅游景点质量和旅游产品等的非饭店因素引起的。

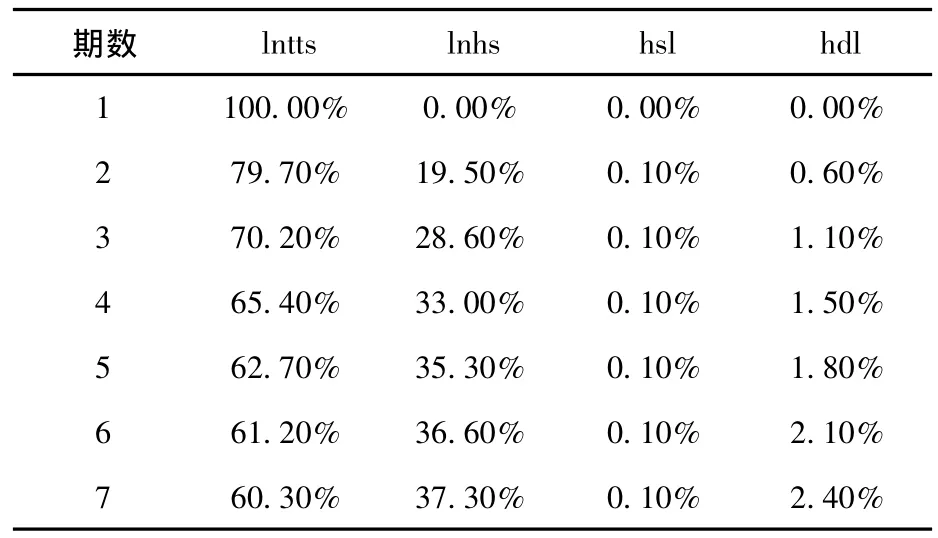
表6 方差分解

5 结论

稳健性参数估计的结果表明，海南省饭店数量和床位数的增加与饭店服务水平的提高将导致当地过夜游客人数的增加，但其作用路径机制是不同的，前者通过自助游游客，后者通过旅行团游客;饭店服务水平的提高同样将有助于吸引游客住宿。饭店业的客房数的减少有助于过夜游客人数的增加可能是因为开房率本身不高，减少客房可节约开支并将资金用于提升饭店的服务，从而提升对游客选择在当地住宿的吸引力;而饭店业的发展规模水平对过夜游客人数无显著影响。总的来看，海南省各市县可以通过提高饭店业的整体服务水平来增强对游客的吸引力。

［1］张晓峒.计量经济学基础［M］.天津:南开大学出版社，2001:341.

［2］W Greene.Econometric Analysis［M］.NJ:Prentice——Hall:Upper Saddle River，2000.

［3］Sosa-Escudero W Yoon M Bera a k.Tests for the error component model in the presence of local misspecification［J］.Journal of Econometrics，2001，101(1):1-23.

［4］Pesaran M H.General diagnostic tests for cross section dependence in panels［M］.U.S:Cambridge University Press，2004.

［5］E W Frees.Longitudinal and panel data:Analysis and applications in the social sciences［M］.U.S:Cambridge University Press，2004.

［6］Wu P X，Baltagi B H.Unequally spaced panel data regressions with AR(1)disturbances［J］.Econometric Theory，1999，15(6):814-823.

［7］Tibshirani R J，Efron B.An Introduction to the Bootstrap［M］.U.S:CRC Press，1994.

［8］Zeger S L，Liang K Y.Regression analysis for correlated data［J］.Annual Review of Public Health，1993，14(1):43-68.

［9］Kraay A C，Driscoll J C.Consistent covariance matrix estimation with spatially dependent panel data［J］.Review of Economics and Statistics，1998，80(4):549-560.

［10］杨继生.线性、非线性面板结构VAR模型的参数、半参数估计［J］.数量经济技术经济研究，2011(3):140-151.