CAPM的新模型研究——基于美国银行信用违约互换数据的研究

邸昊，李柳铃

（南开大学经济学院，天津300071）

CAPM的新模型研究——基于美国银行信用违约互换数据的研究

邸昊，李柳铃*

（南开大学经济学院，天津300071）

采用Jin(2011)以及Zhuo（2013）提出的新模型和新方法，对Sharpe(1964），Lintner(1965)以及Mossin(1966)论文中提出的资本资产定价模型（CAPM）进行了实证研究。本文使用极大似然法对新的模型参数进行了估计。极大似然估计的程序是用MatLab编写的。最后发现，对于美国银行信用违约互换而言，非对称指数幂分布模型（AEPD），以及标准化非对称指数幂分布模型(SSAEPD)都适用。通过比较发现，基于标准化非对称指数幂分布模型(SSAEPD)的资本资产定价模型具有更好的样本适用性。

资本资产定价模型（CAPM)；非对称指数幂分布模型(AEPD)；标准化非对称指数幂分布模型（SSAEPD)；信用违约互换（CDS）

一、前言

根据马科维茨（1959）的投资理论，Sharpe (1964)，Lintner(1965）和Mossin(1966)首度提出了资本资产定价模型（CAPM）。作为现代金融模型的主要参考模型，CAMP理论解释了股票回报率和市场回报率之间的关系。运用CAPM模型所计算出来的斜率（通常被称为beta或者斜率）被广泛运用来衡量市场风险。例如，雅虎金融网站所使用的beta值便是如此。

然而，一些学者指出，CAPM具有其自身的局限性，可以从多个角度提升该模型。所以很多学者对CAPM模型进行了修正和改进。这些改进可以被分为两个大类。一类改进不采用实证数据，比如Lucas (1978)，Breeden(1979)，Grossman和Shiller(1987)提出消费CAPM模型(CCAPM)。Black(1976)，Lee(1986)和Gweon(1986)提出了wealth CAPM(WCAPM)(见表1)。

第二类对模型的修正则使用实证数据研究。一些学者试图找到其他因子替代市场来检验模型。例如，Fama和French（1993）增加了Book-to-market因子和Size因子，是CAPM模型变为三因子模型。Jegadeesh和Titman(1993)提出Momentum因子和数据，该模型使得股票的收益率准确度在短期内表现最优。Al-Horani，Pope和Stark(2003)提出了研究和发展（R&D）因子，用于解释英国股价收益率截面变动。He(2008)提出了State Switch因子。Lu和Gao增加了CME因子以丰富模型。Lu和Gao（2010）以及Chen，Xu和Wang（2010）发现交易和P/E值两个因子加入模型后，可以更好的解释中国股票市场的情况。

不同于之前的研究，Zhuo（2013）认为采用非正太分布的误差项模型，例如SSAEPD模型，可用来实证检验CAPM模型。他发现CAPM模型可适用于美国股票市场，并且CAPM-SSAEPD模型能比CAPMNormal模型更好的描述了市场状态。Zhu和Zinde-Walsh（2009）提出了SSAPED模型，并表明了SSAEPD模型具有理想的统计结果，该模型可以同时嵌套几个其他的分布，并且可以很好的和金融数据配合。对于SSAEPD模型的研究历史，可以从表2中看到。

基于Zhuo(2013)的研究方法和模型，在本文中将实证检验CAPM模型。本文将检验以下假设：1）具有非正太分布残差的CAPM模型是否对美国银行业信用违约互换数据具有适用性？2）CAPMAEPD和CAPM-SSAEPD模型对比，哪个模型更好？本文使用信用违约互换数据的原因在于：自2009年金融危机之后，尤其是希腊主权债务信用评级下跌后，欧洲的主权国家的信用违约互换交易量大幅上涨。同时，主权国家信用违约互换和其他金融产品之间的关系引起了跟多的学者关注。例如，Ammer&Cai（20011）分析了信用违约互换利差和债券回报率之间的关系。关于主权国家信用违约互换的研究历史见表3。

为了解答以上两个假设问题，本文分析了美国三家银行从2004年到2010年的信用违约互换数据，极大似然估计方法（MLE）用于估计参数。似然比检验用于对参数约束条件进行检验，KS检验用于对残差进行检验，使用AIC准则对比模型。

通过验证发现，具有非正太分布残差的CAPM模型对于美国银行信用违约互换具有适用性。AEPD和SSAEPD模型的参数调整检验，可以刻画偏度，非对称性以及肥尾状态。而CAPM-SSAEPD模型比CAPM-AEPD模型具有更好的数据适用性。

本篇文章组织结构如下：第一部分介绍模型和估计方法，第二部分介绍实证数据检验结果，第三部分讨论结论和将来的研究拓展。

表1　CAPM研究历史

续前表

表3　近年来关于主权国家信用违约互换的研究

二、模型和估计方法

（一）模型

1、CAPM-AEPD模型

CAPM-AEPD如下：

此处θ＝（β1，β2，α，p1,p2,σ)为待估计的参数。rt为股票投资组合在时间的回报率。rft是无风险资产收益率。r mt为整个股票市场的收益率。β1和β2为待估计系数，在模型中α∈（0，1）为偏度参数，而T为数据大小。根据Zhu和Zinde-Walsh（2009），ut为非对称指数幂分布(AEPD)下的随机误差项。ut的概率密度函数（PDF）为:

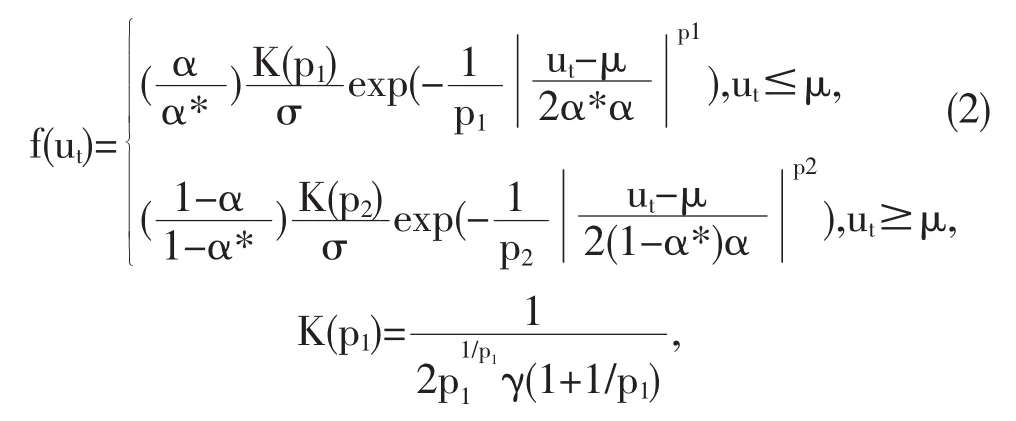
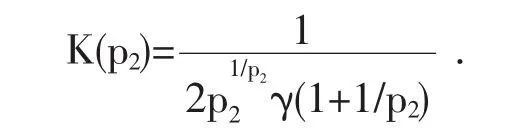
γ(.)为伽马函数。μ∈R为分布位置参数。σ＞0为尺度参数。α∈(0,1)为偏度参数。p1＞0和p2＞0分别为左尾和右尾的参数。

2、CAPM-SSAEPD模型

CAPM-SSAEPD模型如下:

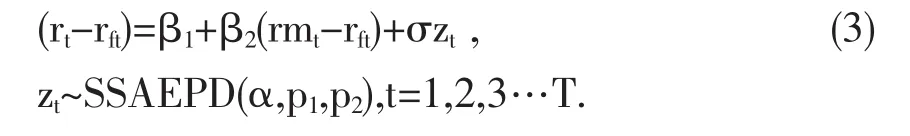
此处(rt,rft,rmt,β1+β2,T,α,p1,p2)具有和CAPMAEPD一样的参数意义。σ在回归模型中为波动参数。残差项zt服从SSAEPD分布,该分布是从SAEPD演变过来的。zt的密度函数是:

xt服从SAEPD分布。此处γ(.)是伽马函数。α∈(0,1)为偏度参数。p1＞0和p2＞0分别为左尾和右尾参数。

（二）极大似然估计法(MLE)

本文运用极大似然估计法(MLE)对下文参数进行估计。

1、CAPM-AEPD模型的极大似然估计

CAPM-AEPD模型的极大似然估计函数为：

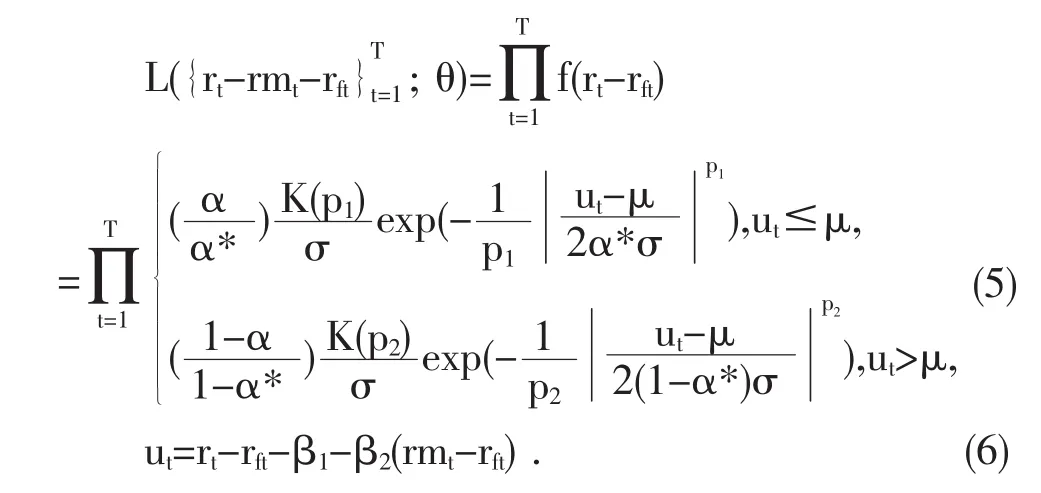
此处θ=(β1,β2,α,p1,p2,μ,σ)为模型中待估计的参数。

2、CAPM-SSAEPD的极大似然估计

CAPM-SSAEPD的极大似然估计函数为：

此处θ=(β1-β2,α,p1,p2,μ,σ)为模型中待估计的参数。

三、实证分析

（一）数据

本文选用了三家美国银行信用违约互换的中间价格，包括美国银行（BOA），花旗银行（CITI），JP摩根（JPM），以上数据均购于CMA Vision company。计算中选用标普500指数作为市场指数，该数据来源于Bloomberg。文中选用的数据样本区间为2004年1月5日至2010年3月31日。银行信用违约互换的对数收益率计算如下：

Ri,t=lnPi,t-lnpi,t-1

此处Pi，t为CDS i在时间t的差价。Ri，t为CDS i差价在时间t的回报率。样本的描述性统计量是使用Eviews进行计算的，计算结果见表4。对于每个银行的CDS而言，偏度不为0，峰度大于3。对每个CDS的Jarque-Bera检验结果都低于5%的显著性水平。以上数据意味着在显著性水平为5%时，CDS数据不服从标准正太分布，因此可以得到结论CDS数据不服从正太分布，而服从于非正太分布。

（二）估计结果

对于CAPM-AEPD模型和CAPM-SSAEPD模型的估计结果见表表5的A栏和B栏。在A栏中，可以发现估计结果中偏度系数α不等于0.5。左尾和右尾的系数均小于2，呈现厚尾状态。同样的，所有的CDS数据的右尾估计值p2更下，这意味着CDS数据的分布右尾呈厚尾状态。也就是说CAPMAEPD模型呈现尖峰厚尾的非对称状态，CAPMSSAEPD模型具有同样的估计结果。

（三）结构分析

三家银行的CDS数据的β2值均大于1，这意味着美国银行CDS数据对市场波动敏感。在CAPMSSAEPD模型中，出了BOA数据外，所有估计的值都大于CAPM-AEPD的对应值。

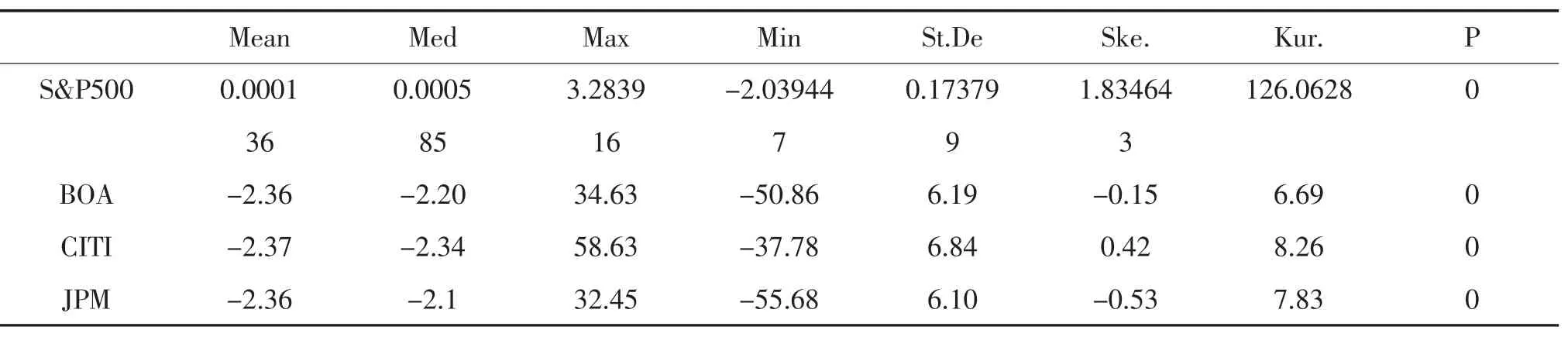
表4　描述统计量

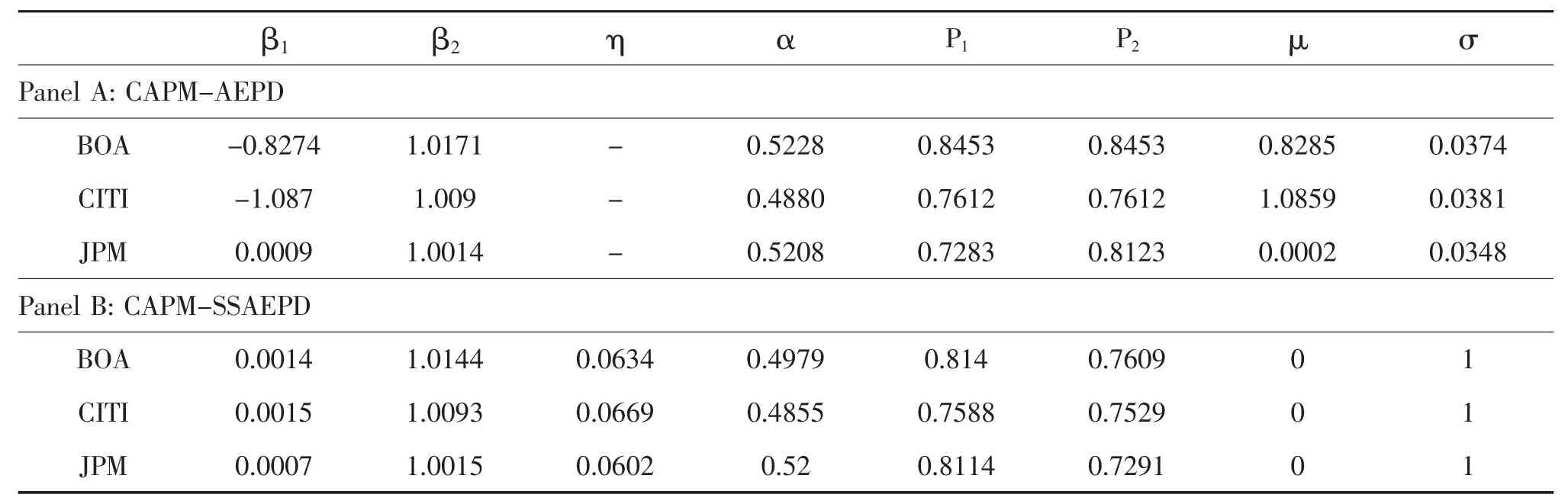
表5　估计结果

表6　LR检验的P值

（四）模型诊断

1、系数的显著性分析

本文运用似然比检测（LR）对模型进行显著性检验。P值和LR值见于表6的A栏和B栏。可得三家银行CDS数据具有回归参数具有显著性。例如在T2中LR的统计学值为0，小于0.05。结果表明在显著性水平为5%的水平下，可以得出系数具有统计学意义并且可以反映股票的收益率水平。

同样，可以发现三家银行的β2值都具有统计学意义(见T3)。在CAPM-AEPD模型，6个连续的参数里有2个显著，而在CAPM-SSAEPD模型中所有的参数均具有显著。

2、残差检验

在这个部分，利用Kolmogorov-Smirnov检验对两个模型的残差进行检验。可以发现，3家银行的CDS数据（不论senior数据或者subordinate数据）均同时服从AEPD和SSAEPD分布。

·Kolmogorov-Smirnov检验

KS的零假设为数据服从某个特定分布。同时设定显著性水平位5%。如果P值大于5%，则接受零假设，否则拒绝零假设。

首先，将KS检验应用于CAPM-AEPD模型，零假设为CAPM-AEPD残差按照AEPD()分布。CAPM-AEPD的P值见表7。对于BOA而言，P值是1，大于0.05，意味着在显著性水平为5%下，不能拒绝零假设，则残差服从于AEPD分布。另外对于其他银行的CDS而言，KS检验值均无法拒绝零假设，则可推断CDS数据服从于AEPD分布。则CAPMAEPD模型是适用于美国银行CDS数据的。

Then,we apply the KS test for the residuals from CAPM-SSAEPD.The null hypothesis of KS is然后对CAPM-SSAEPD模型进行KS检验，零假设为CAPM-SSAEPD的残差服从SSAEPD()。P值见表7。可以得到3家银行的CDS数据均服从于SSAEPD分布。可见CAPS-SSAEPD模型同样适用于美国银行CDS数据。

·残差的密度函数（PDF）

表7　P值

以BOA数据为例，见图1，对比残差的概率密度函数，可以发现服从AEPD()的和残差正太分布非常接近，同时CAPM-AEPD更符合数据。

（五）参数约束检验

在这一个部分，对CAPM-AEPD和CAPMSSAEPD模型参数进行参数约束，并且利用公式（4）中的LR检测。所有测试结果见表6。以CITI为例，结果见表T4，均小于5%的显著性水平，以上结果意味着残差并不服从正太分布。以上结论同样适用于其他两家银行的CDS数据。

（六）模型比较

在这一部分，本文运用AIC检测对CAPMAEPD和CAPM-SSAEPD两个模型进行比较。在表8中，计算了两个模型的AIC值的差，结果显示由于CAPM-SSAEPD模型的AIC值更小，所以优于CAPM-AEPD模型。

图1　：CAPM-AEPD模型残差概率密度函数（BOA CDS，AEPD()）

图2　：CAPM-SSAEPD模型残差概率密度函数（BOA CDS，SSAEPD()）

表8　：CAPM-AEPD和CAPM-SSAEPD模型的AIC差值(DAIC)

另外，本文将有参数约束的模型和无参数约束的模型进行比较，发现CAPM-SSAEPD模型的最小AIC值比CAPM-AEPD模型的最小AIC值还要小，所以最优。

表9　AIC值

四、结论和拓展

在本文中，使用美国三家银行CDS数据实证检验了Sharpe(1964)，Lintner(1965)，Mossin(1966)提出的CAPM理论。极大似然估计法用于预测模型。三家银行的CDS数据区间为2004年至2010年。KS检验用于进行残差检验，LR检验用于不同约束条件先的参数检验，以及显著性水平检验。运用AIC方法进行了模型比较。

实证结果显示：

1）CAPM理论在CAPM-AEPD模型的嵌套下成立。

2）在AIC准则下CAPM-SSAEPD比CAPMAEPD模型更具样本适用性。

3）用于计算美国银行CDS利差的指数可以通过分析银行的资产结构来获得，以获得比S&P500更好的拟合结果。

未来拓展包括但不局限于以下几个方面：首先，可以加入GARCH模型或者随机波动模型(SV)进入CAPM理论中研究，其次，可以比较模型的预测功能。最后可以和ARIMA(p,d,q)模型进行比较。

[1]A itchison J.and Brow n J.A.C.The lognormal distribution w ith special reference to its uses in economics[M].Cambridge U niversity Press,1957,p.176.

[2]A mmer.Sovereign CD S and bond pricing dynamics in emerging markets：D ose the cheapest-to-deliver option matter?[J]Journal of international financial markets institutions and money,2011,21(3)：369-387.

[3]A yebo,A,K ozubow ski T J.A n asymmetric generalization of G aussian and Laplace law s[J].Journal of ProbabilityandStatisticalScience,2004,1(2)：187-210.

[4]A zzalini,A.Further results on a class of distributions w hich includes the normal ones[J].Statistica, 1986,46：199-208.

[5]Bartholdy J.,Peare P.Estimation of excepted return：CA PMvs Fama and French[J].International review of financial analysis,2005,14(4)：407-427.

[6]Black,S W.Rational response to shocks in a dynamic model of capital asset pricing[J].A merican Economic Review,1976,66：767-779.

[7]Carr P.,W u Liuren.Theory and evidence on the dynamic interactions betw een sovereign credit default sw aps and currency options[J].Journal of banking& Finance,2007,31(8)：2383-2403.

[8]Chen,Cathy W.S.,Simon Lin,Philip L.H.Y u.Smooth transitionquantilecapitalassetpricingmodels w ithheteroscedasticity[J].ComputationalEconomics,2012,40：19-48.

[9]Chen,Langnan,StevenLi,JinanW ang.Liquidity, skew ness and stock returns：Evidence from Chinese stock market[J].A sia-Pacific FinancialM arkets, 2011,18：405-427.

[10]D e M oivre,A braham(1738).The doctrine of chances [M].ISBN 0-8218-2103-2.

[11]D iCiccio T,M onti A C.Inferential aspects of the skew exponential pow er distribution[J].Journal of A merican Statistic A ssociation,2004,99(466)：439-450.

[12]Fama,E.F.and K.R.French.Common risk factors in the returns on stocks and bonds[J].Journal of Financial Economics,1993,33：3-56.

[13]Fernandez C,O siew alski J,Steel M F J.M odeling andinferencew ith-SphericalD istributions[J]. Jour nal of the A merican Statistical A ssociation, 1995,90(432)：1331-1340.

[14]G auss,C.F.Theoria M otus Corporum Coelestium. Perthes,H am-burg,1809.Translation reprinted as Theory of the M otions of the H eavenly Bodies M oving aboutthe Sun in Conic Sections.D over,N ew Y ork,1963.

A Study on“CAPM Theory”with Models Based on Non-normal Errors for US Bank CDS

DI Hao，LI Liu-ling
（Institute of Economics，Nankai University,Tianjin 300071，China）

This paper empirically exams“the theory of Capital Asset Pricing Model”(CAPM)presented by Sharpe(1964),Lintner(1965)and Mossin(1966)with Jin's(2011)and Zhuo's methods and models(2013).Method of Maximum Likelihood Estimation,the program of which is written with MatLab,is adopted to estimate the parameters.The results show that models with AEPD or SSAEPD errors are both adequate for US bank CDSs and CAPM model with SSAEPD errors is more suitable in sample applicability.

Capital Asset Pricing Model(CAPM)；Asymmetric Exponential Power Distribution(AEPD)；Standardized Standard Asymmetric Exponential Power Distribution(SSAEPD)；Credit Default Swap(CDS)

F224

A

2095-3763（2015）02-0116-09

2014-10-25

邸昊（1990-），男，河北唐山人，南开大学经济学院本科生。

*通迅作者邮箱：liliuling@nankai.edu.cn