基于蒙特卡罗方法的XRF探测器立体角分析

刘合凡 葛良全 谢希成 赵剑锟 罗耀耀

基于蒙特卡罗方法的XRF探测器立体角分析

刘合凡 葛良全 谢希成 赵剑锟 罗耀耀

（成都理工大学 地学核技术四川省重点实验室 成都 610059）

为研究探测器立体角在X射线荧光(X-ray fluorescence, XRF)分析仪的设计对测量结果的影响，运用蒙特卡罗方法对XRF仪进行建模。结果表明，探测器脉冲计数随着探测器与样品之间距离的增大指数衰减；随着探测器立体角的增大，特征峰计数非线性增大，源峰探测效率指数递减；探测器本征探测效率与探测器立体角无关。本文研究方法和结论可为一些XRF仪的设计提供参考。

探测器立体角，X荧光分析，蒙特卡罗方法，拟合优度

在元素分析领域，X射线荧光(X-ray fluorescence, XRF)分析仪是最重要的分析仪器类型之一，广泛应用于采矿、环保、石化、材料、食品等领域[1–5]。XRF测量中，仪器计数率不仅与待测试样本身的物理化学性质有关，还与激发源、试样、探测器的相对几何位置有关[6–8]。探测器的安放位置不同，所形成的探测器立体角不同，从而使仪器探测效率也不一样。在可接受误差范围内，应尽量提高仪器荧光计数和探测效率，进而提高分析精度和缩短分析时间。而经大量学者研究，美国洛斯阿拉莫斯实验室的通用大型蒙特卡罗程序MCNP软件已经成为核技术领域谱数据模拟和分析的重要软件之一[9–13]。该软件的模拟数据在其相对误差小于5%的前提下，运用建模模拟计算方法预测谱线强度的准确度约达95%，而用该方法模拟未知成份样品，其预测准确度也能达90%–97%[14]。本文运用MCNP软件参考实际荧光分析仪的具体情况进行建模，通过改变探测器立体角得到模拟计算结果，以观察探测器立体角对XRF测量结果的影响情况。

1 理论基础

1.1 探测器立体角的计算

设α为激发源光子在样品o点处激发待测元素特征X射线时的入射角，β为样品o点处产生待测元素特征X射线对应的出射角。显然激发源出射射线在样品中的激发位置不同，α、β的大小也不一样，如图1所示。

图1 X射线荧光测量中立体角关系推导示意图Fig.1 Schematic diagram of deriving the desired X-ray collection angle in XRF measurement.

式中，dΩ单位为sr（球面度）。

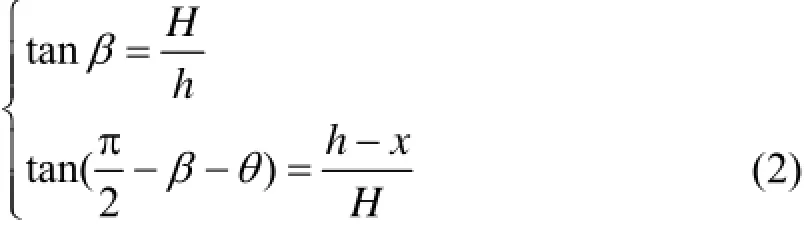
于是：

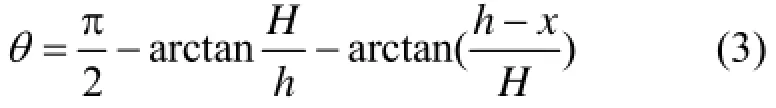
将式(3)代入式(1)，则探测器相对于x点的立体角为：

1.2 拟合优度评价

面对大量的数据分析工作，往往需要通过一定的方程拟合才能够发现数据之间的确切关系。而方程拟合的好坏直接揭示了数据之间内在关系的准确性，一般情况下用“拟合优度”这一物理量来表征曲线方程对数据拟合程度的好坏。度量拟合优度的统计量用“确定系数”R2表示，计算公式为：

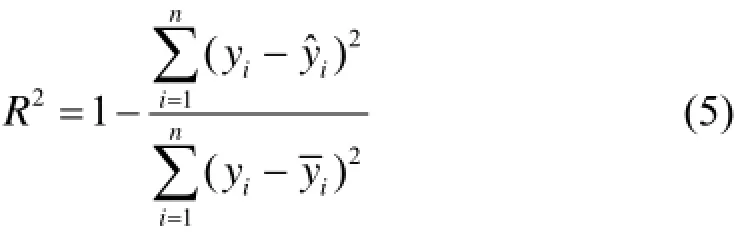
式中，n表示原始数据个数；yi表示第i个原始数据；表示对应的第i个拟合数据；表示原始数据均值。粗略地讲，拟合值R2越高，则说明方程对离散点拟合得越好；R2值越低，方程对离散点拟合得越差[15]。从式(5)可以看出，R2取值在0–1之间。R2越接近于1，说明模型选择和拟合越好，数据预测也越成功。特别对于线性拟合，R2越大，则回归方程拟合数据越好，线性关系越强。

2 蒙特卡罗模型

本文模型以待测样品下平面正中心为原点，平行样品建立Y坐标，垂直样品建立Z坐标，如图2所示。

激发源真实模拟美国Moxtek公司TUB00083系列X光管，采用半径为0.04cm的面源，光子在面源内进行高斯分布型均匀抽样；出射粒子方向与−Y方向夹角45°，散射角度为±23°，粒子抽样参考方向与−Y方向夹角45°，抽样概率为0:1；抽样粒子能量为0.050MeV。探测器真实模拟美国Moxtek公司XPIN-XT系列探测器，部分结构做了适当简化。探测器中轴线与样品+Y方向夹角45°，探测器晶体为正圆柱，晶体横截面积为13mm2，厚度为625μm；Be窗厚度为8μm，保护壳材料为纯铝。探测器晶体镀有一层二氧化硅保护膜，膜厚度为1μm；铍窗与保护膜之间填充空气。待测样品为纯元素样品，粒度理想，分布均匀，尺寸为ø5cm×1cm。模型截断球内填充空气，截断球外用真空填充。模型计数采用F8数据卡，记录探测器中脉冲数的能量分布，计数对象为探测器晶体部分。能量箱设置有0能量箱（空箱）、Epsilon能量箱以及常规能量箱。空箱用以记录捕获否定的、非模拟的电子碰撞记录；Epsilon能量箱用来记录穿过探测器而未被探测器记录的粒子数；常规能量箱能量范围为1.01×10−5–0.050MeV。能量之间进行线性插值，共记录1024道能量计数，模拟探测器响应的每一道道址能量均与实验仪器保持一致。设置激发源粒子抽样个数为2×108个，模拟相对误差小于2%。

图2 蒙特卡罗方法模拟X射线荧光测量系统空间几何布置图Fig.2 Geometric layout for XRF measurement system by Monte Carlo method.

对于一个固定几何位置的已知探测器，其最大立体角应当为定值。本文通过改变探测器晶体轴心位置（沿Z轴正方向，如图2所示）产生相对于入射原级X射线对样品激发点x处的探测器立体角变化，从而研究不同探测器立体角引起待测元素特征峰计数的变化情况。除H值变化外，探测器其他参数均保持不变。

3 结果分析

3.1 特征峰计数与“探测器-样品”距离H的关系

在激发源和样品相对位置保持不变的情况下，探测器脉冲计数随着探测器与样品之间距离H的增大呈指数衰减，如图3所示。随着激发源与样品之间距离H的逐渐加大，激发源入射原级X射线在样品表面的照射量变小，激发样品待测元素所产生特征X射线的概率也在变小，从而导致了探测器脉冲计数的减小。

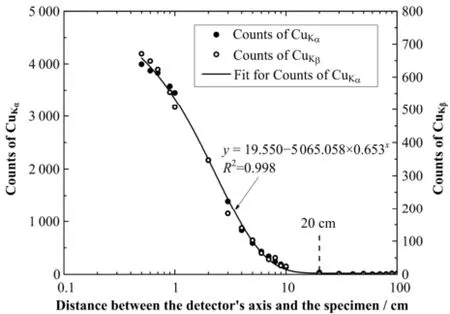
图3 蒙特卡罗方法模拟Cu样品特征峰计数与探测器轴心距离的关系Fig.3 Relationship between Cu's X-ray characteristic fluorescence peak counts and ‘detector axis to specimen' distance by Monte Carlo calculation.

由图3可以看出，当H值大于20cm时，探测器脉冲计数基本降为0。分析原因，除了空气对射线的有限吸收作用外，在H值大于20cm时出射特征X射线几乎已处于探测器立体角之外，即探测器已基本探测不到出射特征X射线，故特征峰计数几乎为0。

3.2 特征峰计数与探测器立体角的关系

以式(4)计算出探测器立体角并将其作为横坐标，得出特征峰计数与探测器立体角的关系，如图4所示。

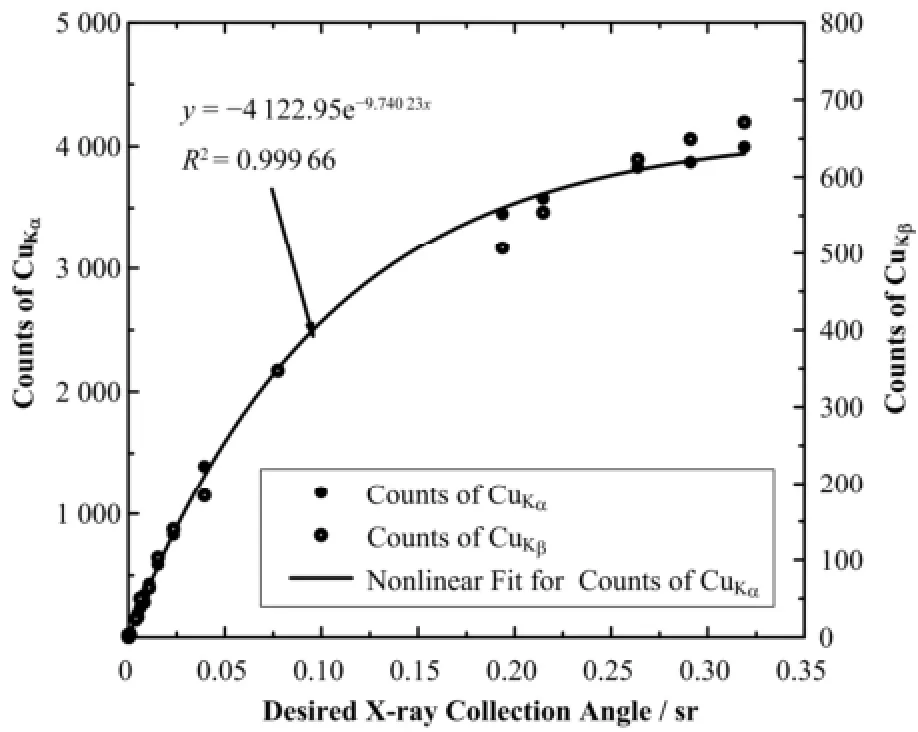
图4 蒙特卡罗方法模拟Cu样品特征峰计数与探测器立体角的关系Fig.4 Relationship between Cu's X-ray characteristic fluorescence peak counts and the desired X-ray collection angle by Monte Carlo calculation.

图4 中，随探测器立体角的逐渐增大，特征峰计数非线性增大，对CuKα脉冲计数进行指数拟合，拟合优度为0.99966。

3.3 探测效率与探测器立体角的关系

根据峰总比和源峰探测效率的计算公式[16]，得出模型探测器峰总比和源峰探测效率数值，并以探测器立体角作为横坐标，得到关系如图5所示。

图5 蒙特卡罗方法模拟Cu样品峰总比、源峰探测效率与探测器立体角的关系Fig.5 Relationship of the Cu's ‘peak to source' ratio, ‘peak to total' ratio and the desired X-ray collection angle by Monte Carlo calculation.

由图5可以看出，随着探测器立体角的增大，源峰探测效率成指数递减，而峰总比却基本保持不变，维持在76.96%左右。这一结果与张明等[17]对NaI(Tl)探测器探测效率的模拟结果一致。

随着探测器立体角变小，探测器沉积X射线的几率变小，全能峰计数必然降低，故源峰探测效率变小。但由于立体角变小的同时，全谱计数也跟着变小，故峰总比不一定会变小。图5显示了峰总比并不随探测器立体角而变化。根据峰总比定义，探测器本征探测效率也必定保持恒定值，即探测器本征探测效率与探测器立体角无关。

4 结语

本文根据具体的XRF仪进行蒙特卡罗建模，分析了探测器立体角与特征峰计数和探测效率的关系，得出结论如下：

(1) 探测器脉冲计数随着探测器与样品之间距离的增大指数衰减；

(2) 随着探测器立体角的增大，特征峰计数非线性增大；

(3) 随着探测器立体角的增大，源峰探测效率指数递减；

(4) 探测器本征探测效率与探测器立体角无关。

1 李建胜, 王仁波, 周蓉生, 等. 高灵敏度野外X荧光分析系统及其在铜矿勘探中的应用[J]. 核技术, 2002, 25(3): 211–218

LI Jiansheng, WANG Renbo, ZHOU Rongsheng, et al. A fieldwork high-sensitivity X-ray fluorescence analysis system and its application on exploration of copper mine[J]. Nuclear Techniques, 2002, 25(3): 211–218

2 唐尧基, 樊静, 冯素玲. 环境水样中痕量肼的荧光分析[J]. 分析试验室, 2003, 22(1): 48–52

TANG Yaoji, FAN Jing, FENG Suling. Fluorimetric method for determination of trace hydrazine in environmental water samples[J]. Chinese Journal of Analysis Laboratory, 2003, 22(1): 48–52

3 管嵩, 丁仕兵, 王越, 等. X荧光光谱法测量高钛渣中主次元素[J]. 分析测试学报, 2012, 31(Z1): 198–202

GUAN Song, DING Shibing, WANG Yue, et al. Determination of major and minor components in high-titanium slag by X-ray fluorescence spectrometry[J]. Journal of Instrumental Analysis, 2012, 31(Z1): 198–202

4 任翔, 葛良全, 张庆贤, 等. 原位X射线荧光测井井液的影响与校正[J]. 核技术, 2009, 32(10): 756–760

REN Xiang, GE Liangquan, ZHANG Qingxian, et al. A method to correct effect of drilling fluid on in situ X-ray fluorescence logging[J]. Nuclear Techniques, 2009, 32(10): 756–760

5 高华娜, 赵海英, 王志宙, 等. 螺旋藻的PXRD和XRF分析[J]. 食品科技, 2008, 33(12): 270–273

GAO Huana, ZHAO Haiying, WANG Zhizhou, et al. Analysis on the spirulinas by PXRD and XRF[J]. Food Science and Technology, 2008, 33(12): 270–273

6 Mc Neillfe C. Optimization of measurement distance of109Cd K XRF system for obese subjects[J]. Nuclear Science and Techniques, 2003, 14(1): 86–89

7 刘艳芳, 赖万昌, 谢希成, 等. 能量色散型X荧光分析仪光管、样品、探测器距离的蒙特卡罗优化[J]. 核电子学与探测技术, 2011, 31(9): 1038–1042

LIU Yanfang, LAI Wanchang, XIE Xicheng, et al. Optimization of the distance among the detector, tube and samples in the EDXRF analyzer by the Monte Carlo method[J]. Nuclear Electronics & Detection Technology, 2011, 31(9): 1038–1042

8 Dryak P, Kovar P. Experimental and MC determination of HPGe detector efficiency in the 40–2754 keV energy range for measuring point source geometry with the source-to-detector distance of 25 cm[J]. Applied Radiation and Isotopes, 2006, 64(23): 1346–1349

9 San Miguel E G, Perez-Moreno J P, Bolivar J P, et al. A semi-empirical approach for determination of low-energy gamma-emmiters in sediment samples with coaxial Ge-detectors[J]. Applied Radiation and Isotopes, 2004, 61(2–3): 361–366

10 He J, Zhang C M. The accurate calculation of the Fourier transform of the pure Voigt function[J]. Journal of Optics A: Pure and Applied Optics, 2005, 7(10): 613–616

11 Gardner R P, Sood A, Wang Y Y, et al. Single peak versus library least-squares analysis methods for the PGNAA analysis of vitrified waste[J]. Applied Radiation and Isotopes, 1997, 48(10–12): 1331–1335

12 陆安详, 王纪华, 潘立刚, 等. 便携式X射线荧光光谱测定土壤中Cr、Cu、Zn、Pb和As的研究[J]. 光谱学与光谱分析, 2010, 30(10): 2848–2852

LU Anxiang, WANG Jihua, PAN Ligang, et al. Determination of Cr, Cu, Zn, Pb and As in soil by field portable X-ray fluorescence spectrometry[J]. Spectroscopy and Spectral Analysis, 2010, 30(10): 2848–2852

13 Sharshar T, Elnomer T. Efficient calibration of HPGe detectors for volume-source geometries[J]. Applied Radiation and Isotopes, 1997, 48(5): 695–697

14 Vincze L, Janssens K, Adams F, et al. A general Monte Carlo simulation of EDXRF spectrometer II: polarized monochromatic radiation, homogeneous samples[J]. Spectrochimica Acta, 1993, B50(3): 127–147

15 赵松山. 对拟合优度R2的影响因素分析与评价[J]. 东北财经大学学报, 2003, 3(27): 56–58

ZHAO Songshan. Analysis on factors affecting the goodness of fit R2[J]. Journal of Dongbei University of Finance and Economics, 2003, 3(27): 56–58

16 乔录成, 白立新, 张一云, 等. 高纯锗γ谱仪对环境样品探测效率的模拟计算[J]. 四川大学学报(自然科学版), 2003, 40(2): 301–305

QIAO Lucheng, BAI Lixin, ZHANG Yiyun, et al. Simulating calculation of the HPGe γ-spectrometer detection efficiency for environmental samples[J]. Journal of Sichuan University (Natural Science Edition), 2003, 40(2): 301–305

17 张明, 王仁仲, 杨元第, 等. 蒙特卡罗方法模拟激发源位置对井型NaI(Tl)晶体探测效率的影响[J]. 核电子学与探测技术, 2012, 32(1): 50–54

ZHANG Ming, WANG Renzhong, YANG Yuandi, et al. Influence of the source position to the well type NaI(Tl) detection efficiency based on a Monte Carlo simulation[J]. Nuclear Electronics & Detection Technology, 2012, 32(1): 50–54

CLC TL8, O657.3

Calculation of desired X-ray collection angle on XRF analyzer designed by Monte Carlo method

LIU Hefan GE Liangquan XIE Xicheng ZHAO Jiankun LUO Yaoyao
(Chengdu University of Technology, Key Laboratory of Applied Nuclear Techniques in Geosciences, Chengdu 610059, China)

Background: The designing of the X-ray fluorescence (XRF) analyzer's geometric layouts need to be considered, such as ‘detector to specimen' distance, ‘detector to source' distance, ‘source to specimen' distance. The desired X-ray collection angle is one of the important factors of the detection performance. However, the experience geometric layouts have been unable to meet every XRF analyzer designing, because the performance of the excitation source or the detector is getting better, sample processing technology is much more advanced, and so on. Purpose: The aim is to study the impact of the desired X-ray collection angle on XRF analyzer designing, and provide a technical guidance on methodologies for XRF analyzer designing. Methods: In this paper, we build the XRF analyzer models by the Monte Carlo method and analyze the impacts of the desired X-ray collection angle on XRF analyzer designing. Results: Kinds of factors with the desired X-ray collection angle are analyzed, such as Cu's X-ray characteristic fluorescence peak counts, the ‘detector axis to specimen' distance, the Cu's ‘peak to source' ratio. Conclusions: With the increasing of distance between the detector and the specimen, the detector's pulse counts satisfy an exponential decay law. With the desired X-ray collection angle increasing, the Cu's X-ray characteristic fluorescence peak counts increase linearly. With the desired X-ray collection angle increasing, the ‘peak to source' ratio decays exponentially, but the ‘peak to total' ratio remains the same.

Desired X-ray collection angle, XRF analysis, Monte Carlo method, Goodness of fit

TL8，O657.3

10.11889/j.0253-3219.2015.hjs.38.060502

国家863计划项目(No.2012AA061803)、国家自然科学基金(No.41074093)资助

刘合凡，男，1983年出生，2010年于成都理工大学获硕士学位，现为博士研究生，研究方向为核信息获取与处理

葛良全，E-mail: glq@cdut.edu.cn

2014-09-22，

2014-11-20